Поля и спектры одномерного фотонного кристалла с дефектом инверсионного типа

Одномерные слоисто-периодические структуры или фотонно-кристаллические структуры (ФКС), представляющие собой слоисто-периодические структуры (СПС), созданные на основе различных материалов, в последние годы обращают на себя пристальное внимание исследователей. Благодаря возникновению в фотонном спектре ФКС запрещённых зон, эти структуры обладают уникальными оптическими свойствами [1-4]. Большое внимание при этом уделяется изучению модификации фотонного спектра ФКС в результате формирования различных нарушений периодичности структуры. Так, наличие в ФКС «дефекта», нарушающего периодичность, приводит к возникновению в запрещённых зонах бездефектной структуры узких полос пропускания (дефектных минизон), что может быть использовано для эффективного управления параметрами распространяющегося излучения [5-9].

В работе [10] приведена классификация дефектов, которые могут быть одиночными и неодиночными, меняющими и сохраняющими число слоёв в исходной периодической структуре, состоящими из материала структуры или нового материала (внедрения, замещения, перестановки, инверсии и другие). Наименее изученными среди указанных дефектов являются дефекты инверсионного типа, которые в простейшем случае состоят в изменении порядка следования слоёв в одной из двух частей структуры. Создание дефекта инверсии с технологической точки зрения оказывается предпочтительней дефектов внедрения и замещения, так как не требует введения в структуру слоёв из дополнительного материала.

В настоящей работе исследуется влияние дефектов инверсионного типа на спектры пропускания одномерной ФКС и на распределение в ней волнового поля. Анализируется зависимость степени локализации волнового поля в области симметричного дефекта от величины диэлектрической проницаемости в соседних слоях, обсуждается возможность формирования спектральной линии дефектной моды заданной формы.

Полев фотонно-кристаллической структуре

Рассмотрим одномерную ФКС, период L которой состоит из слоёв различных оптически изотропных диэлектриков с толщинами L_x, L₂ и диэлектрическими проницаемостями (ДП) е,, е₂. Будем считать, что в исследуемом диапазоне частот поглощением материалов слоёв можно пренебречь, поэтому ДП являются действительными величинами. Магнитные проницаемости слоёв Ц[ и ц₂ будем считать равными единице. Такая структура обладает свойствами одноосного кристалла с осью симметрии n 11 OZ , перпендикулярной границам раздела слоёв. Среда, в которую помещена ФКС, является вакуумом. Будем считать, что волна в структуре распространяется вдоль её оси периодичности, т.е. вдоль оси OZ. В этом случае решение уравнений Максвелла приводит к двум ортогонально поляризованным собственным волнам с компонентами поля (Е-   0) и (Я,, E_v, 0)

соответственно. Зависимость их от времени выберем пропорциональной множителю exp(zcoZ). Опуская эти множители, определим в каждом слое компоненты поля для волны первого типа:

Etj = Aj exp ^-ikjZ^ + В exp Qk^, yj k0 dz где kj дом из

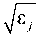
— константа распространения в каж-0=®/с, со и с - частота и скорость волны в вакууме. Распределение электрического поля в каждом из N слоёв структуры может быть представлено в виде:

Е_хХ = А_х cxp(-ik,z) + В_х exp^z), 0 <  z < z_x,

^E,N = ^ЛУ ^еХР V^4kN (^Z " ^ZNA )] ⁺

+ B_N exp ^ik_N (z - z_N__x)], z_N__xN.

Выражения для магнитного поля в каждом из слоёв можно найти с помощью выражений (1) и (2).

После этого из условия непрерывности компонент поля Е и Н та границах раздела всех слоёв получаем систему уравнений для определения коэффициентов А и В_у:

2 УУУУУ'У

где Lj=zj-zj_1 - толщина j-vo слоя, j = 1, ...,N . Полагаем, что при z = 0 в структуру вводится излучение с амплитудой Ао. Так как на выходе из струк туры отсутствует падающая на неё волна, BN = 0 . С помощью системы уравнений (2) и (3) можно последовательно определить амплитуды поля в каждом слое структуры и соответственно распределение плотности энергии поля по структуре.

Указанный алгоритм нахождения поля в слоистой структуре справедлив для произвольного (периодического и непериодического) чередования слоёв. В случае бинарной периодической структуры удобно ввести двухкомпонентный вектор Fy с компонентами Е Н и передаточную матрицу М одного периода структуры, которая связывает амплитуды волнового поля в начале и конце /-го периода: F, (z;) = М¥г (Zj + Е). Компоненты этой матрицы имеют вид:

Ми

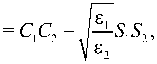
мхг

М1Х

Мгг

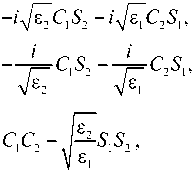
где введены обозначения С- = coskE_p S^sinkEj [9,10]. Так как слои предполагаются непоглощающими, их диэлектрические проницаемости являются вещественными величинами. При этом матрица М унимодулярна и её определитель равен единице [9-11].

Коэффициенты прохождения периодической ФКС

Связь волновых полей в плоскостях, отстоящих друг от друга на целое число периодов (z = 0, z=NL), определяется матрицей преобразования М :

Нх№ = (M’XHA0MMNX2Ey(P), Еу(NL) = (MN )2| Я (0) + (MN )22 Ey (0), которая является целой степенью передаточной матрицы одного периода MN =(му . Через элементы матрицы MN для бездефектной ФКС могут быть выражены амплитудные и энергетические коэффициенты прохождения и отражения [9-11]. Так, амплитудный коэффициент прохождения ФКС определяется выражением

______________И _______________ (6)

а энергетический коэффициент 7-^^. Здесь п_р ⁼ лЯ ^{и Mj =} V^ ~ показатели преломления сред, граничащих с ФКС со стороны входа и выхода излучения соответственно. В дальнейшем при численном моделировании будем считать эти среды вакуумом, поэтому п_р = и = 1 . В качестве материалов слоёв структуры рассматривались арсенид и нитрид галия (GaAs и GaN) с диэлектрическими проницаемостями 8, =11,9 и s₂=5,84 соответственно. Указанные материалы имеют один тип кубической симметрии 43m кристаллической решётки и технологически совместимы. Период структуры L = L, + £₂ = 2,5 мкм.

На рис. 1 представлена частотная зависимость энергетического коэффициента прохождения для периодической ФКС, состоящей из N = 20 периодов и не содержащей дефектов (кроме внешних границ). Указанную структуру для краткости мы будем обозначать формулой М1 . Спектры пропускания такой структуры TN (о), построенные для двух значений параметра 0 = £, / £2 = 1 (рис. 1а) и 0 = и2/И[ =0,7 (рис. 16), состоят из чередующихся областей пропускания и практически полного непропускания излучения. Узкие области непрозрачности, в которых коэффициент пропускания практически равен нулю, в общем случае лежат в частотных интервалах, включающих частоты со, =/соо, / = 1; 2; 3; ... При этом в областях пропускания для структуры с полным числом периодов N наблюдаются осцилляции коэффициента пропускания, число которых равно ^-l. Характер расположения зон непрозрачности и их ширина, амплитуда осцилляций коэффициента пропускания определяются типом распределения диэлектрической проницаемости в СПС. Так, для структуры с одинаковой оптической толщиной соседних слоёв (nvLv = и2£2 = £0 и £, / £2 = и2 / и, ) в спектре отсутствуют чётные, а проявляются только нечётные (/ = 1; 3;...) запрещённые зоны, ши- рина которых в этом случае максимальна. Таким образом, изменяя отношение толщин соседних слоёв в периоде СПС, можно управлять как шириной зон непрозрачности и их расположением в спектре, так и величиной коэффициента пропускания в заданном интервале частот.

минизоны пропускания в запрещённой зоне бездефектного кристалла. Далее на представленных рисунках приведены спектры пропускания и распределения полей в ФКС с одним или несколькими дефектами инверсионного типа. Указанные спектры получены на основе соотношения

Н В||||||

П®) =

|^

+ 5'12+У1+У2|2

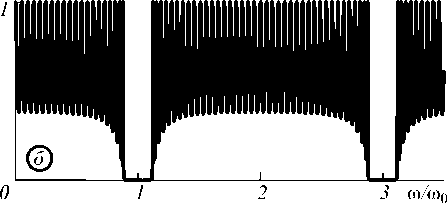
Рис. 1. Спектры прохождения для бездефектной ФКС с 0 = 1;0,7 (а, б)

Спектры и распределение поля в дефектной ФКС

Дефектом ФКС будем считать один или несколько слоёв, занимающих «не своё» место в структуре и нарушающих её периодичность. К важным дефектам периодической структуры необходимо отнести инверсию, которая в простейшем случае заключается в изменении в одной из двух частей структуры порядка следования слоёв на противоположный, т.е. (N^.y —> (N,N_X )". Этот тип дефектов можно сокращённо определить следующими двумя формулами: (МУ(МУ или <му<му, если инверсия име

где ^р - элементы передаточной матрицы ФКС с дефектом. В дальнейшем вычисления проводились для структур без учёта поглощения, поэтому передаточная матрица 5 дефектной структуры является унимодулярной.

На рис. 2 представлена первая зона непропуска-ния в спектрах пропускания бездефектной ФКС (7W)²⁰ (рис. 2а) и ФКС с дефектом, возникающим при инверсии одной части структуры относительно другой - (MfdMf и Шу'ШГ (рис. 26, в). Сплошным кривым отвечают спектры ФКС с одинаковой оптической толщиной соседних слоёв n_xL_x = п^Ц (6 = и, / п_х =0,7 ), пунктирным кривым отвечает структура с L_x = Ц (0 = 1). При равенстве оптических толщин слоёв максимум пропускания отвечает центральной частоте зоны непропускания бездефектной структуры ®₀ = 1,326-10¹⁴ s'¹. Симметричность структуры относительно расположения дефекта приводит к максимально возможному значению коэффициента пропускания 7'(о>₀)=1 в де-

ет место для целого числа периодов (дефект возникает на границе слоёв соседних периодов). Здесь и в дальнейшем символ М означает период структуры

с изменённым

порядком следования слоёв, т.е. ин-период. Если же инверсия охватыва-исло периодов (т.е. дефект возникает едних слоёв одного из периодов), то вертированной структуры являются ' или <МУ⁺'^пу мУ"^+ь. В приведён-исходному периоду отвечает переда

точная матрица М = N_x ■ N₂, а инвертированному -

матрица м = У-У, где у и у - передаточные матрицы отдельных слоёв. Матричные элементы передаточной матрицы инвертированного периода связаны с элементами матрицы нормального периода соотношением (М)^ = Wy,^ , где а, ₽ = 1,2 . Наличие подобного дефекта вызывает изменения в спектре пропускания ФКС и приводит к появлению

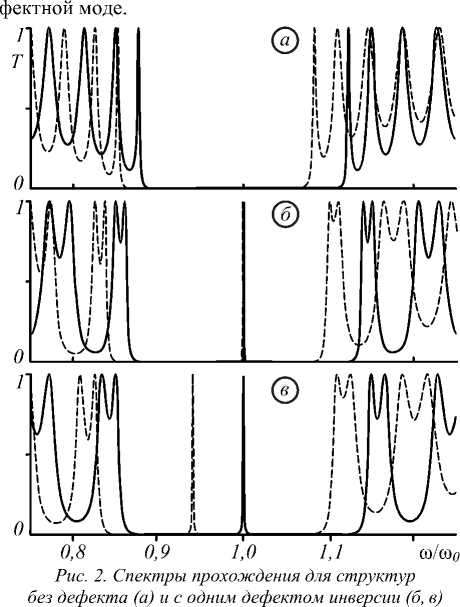
Ширина зоны непрозрачности и положение дефектной минизоны для рассматриваемых структур существенно различны. В ФКС с равными толщинами слоёв дефектная минизона смещена относительно центра запрещённой зоны: в сторону больших частот для структуры (М)10 (М)10 и в сторону меньших частот для структуры (My'XMf. Для обоих типов структур в случае одинаковой оптической толщины слоёв дефектная минизона формируется в центре запрещённой зоны. Ширина зоны непрозрачности дефектной структуры в этом случае является самой большой для всех допустимых значений параметра 0 . Спектральная ширина дефектной моды существенно зависит от значения ДП слоёв в области дефекта. У структуры с повышенным значением ДП в области дефекта ширина минизон пропускания намного шире, чем у структуры с пониженным значением. Ширина дефектной минизоны для каждой из двух типов рассматриваемых структур связана с добротностью соответствующего ФК-микрорезонатора соотношением дсоу = о0 / Qj.

Величину добротности структуры с достаточной степенью точности можно оценить выражением [12]:

Q=^.

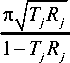
где Х_о - длина волны в вакууме, отвечающая частоте ю₀, К и R_f - коэффициенты пропускания и отражения отдельных ФК-зеркал, которые существенно зависят от числа и порядка следования слоёв с большим и меньшим показателем преломления в зеркалах. Видно, что в случае резонаторной микрополости с меньшим показателем преломления и ширина минизоны будет меньше.

На рис. 3 приведено распределение квадрата напряжённости волнового электрического поля по ФКС с двумя рассмотренными дефектами инверсионного типа. Характер распределения и степень локализации поля на дефекте существенно зависят от типа дефектной структуры.

Так, для структуры (Л/)10 (Л/)10 поле максимально локализуется на самом дефекте, т.е. границе нормальной и инвертированной частей структуры, где достигается максимальное значение плотности энергии (рис. Зя). Симметрично расположенные боковые максимумы поля локализованы на границах соседних периодов структуры, а минимумы поля отвечают границам соседних слоёв в каждом из периодов. В структуре (М)10(М)10 на самом дефекте поле отсутствует, а максимальной локализация поля оказывается на границах соседних слоёв в каждом из периодов (рис. 36). При этом степень локализации в этой структуре оказывается на порядок меньше, чем в структуре (Л/)10(Л/)10.

Формирование первой зоны непропускания и дефектной спектральной линии представлены на рис. 4

для инвертированных структур ^My⁺'^i:\MY¹⁺“ и ^МУ^¹¹ ^М^¹¹*¹¹ (сплошная и пунктирная кривые), у которых инверсия охватывает полуцелое число периодов. Спектры построены при значении параметра 0 = 0,7 для трёх значений числа периодов в структуре N = 2а +1 = 7; 11; 15 . Видно, что с ростом параметра а спектральная линия дефектной моды сужается и более резкими становятся границы запрещённой зоны ФКС. Анализ также показывает, что увеличение числа слоёв в СПС в случае симметричного расположения дефекта приводит к уменьшению спектральной ширины дефектной минизоны, но не влияет на её положение в спектре пропускания и на величину максимума Т^(й_ц^ . При этом степень локализации поля в области дефекта существенно увеличивается. Так, при увеличении числа периодов в структуре на 2 (по одному в исходной и инвертированной частях структуры) квадрат амплитуды поля в максимуме увеличивается в два раза, т.е.

|£_max(« + l)M|£_max(m)|². \Е/Е₀\²

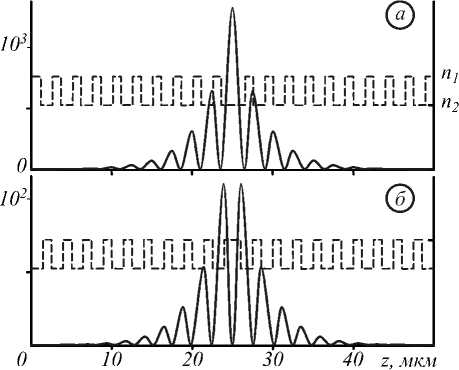
Рис. 3. Распределение плотности энергии волнового поля

в ФКС (ДУ)¹⁰ (Л/)¹⁰ (а) и (М)¹⁰ (М)¹⁰ (б)

Отметим, что положение дефектного слоя в структуре существенно влияет на степень локализации поля на дефекте.

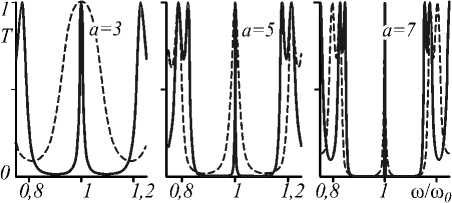
Рис. 4. Спектральная линия дефектной моды для двух типов структур с дефектом инверсии

В табл. 1 приведены максимальные значения плотности поля | Етах / Ео |2, достигаемые на дефекте инверсионного типа в структурах (Л7)Я(М)20^ и фектной структуре, а при смещении дефекта на один х2о-„                                              период ко входу излучения в структуру, т.е. при

(М) (М) при различных значениях параметра а - 9 а . Обращает на себя внимание тот факт, что максимум усиления наблюдается не на симметричной де

Таблица 1. Значения величины ( Emax / Ео |“ для двух типов структур

а            5          6          7           8            9           10          И	12
М"М^"      145,2     297,5     596,1      1125,5      1683,7      1322,9      399,7	63,5
уру-р-1       12,2       24,9       49,9        94,6        141,4        110,9       33,5	5,3

На рис. 5 представлены спектры пропускания и форма спектральных линий дефектных мод, полученные для структур (МУ(МУ и (МУ (М)6 (сплошные и пунктирные кривые) при изменении числа неинвертированных и инвертированных периодов (я = 7...П, Ъ = 20-а), но при сохранении полного числа периодов (а+b=20). Видно, что сдвиг дефекта от центра структуры приводит к уменьшению интенсивности дефектной линии и увеличению её ширины. При этом ширина линии дефектной моды структуры (МУ(МУ намного уже, чем ширина линии структуры (М)° (М)ь . От метим, что спектры со значениями параметров а = 9, b = 11 и а = 11, b = 9 идентичны. Идентичными также должны быть спектры инвертированных структур, отвечающие параметрам (а, b = N-a) и ( N — a, b = а \

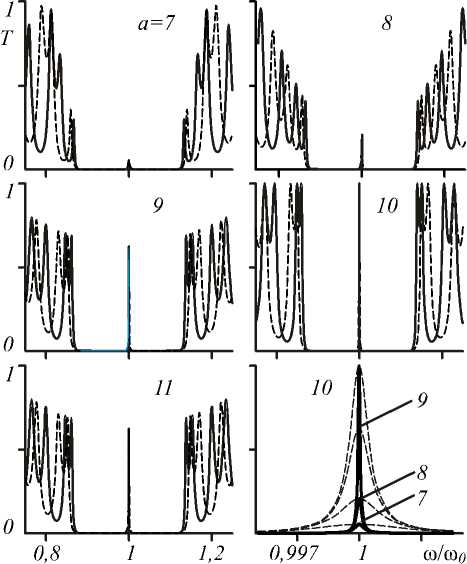
Рис. 5. Спектры пропускания и спектральные линии дефектных мод для ФКС (I У (М)1, (сплошная линия) и (МУ (М(ь (пунктирная линия)

На рис. 6 представлены спектры пропускания, полученные для структуры (Z У (МУ(М)^а, у которой число боковых неинвертированных периодов остаётся неизменным ( а = 5 ), а число центральных инвертированных периодов изменяется ( b = 3; 5; 7; 9; 11).

выше указанная струк-что и определя-запрещённой зоне ФКС. инвертирован-дефектные моды, начинают

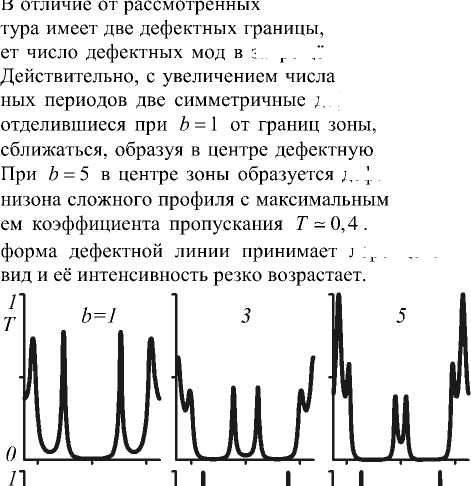
минизону, дефектная ми-значени-

При b =9 лоренцевский

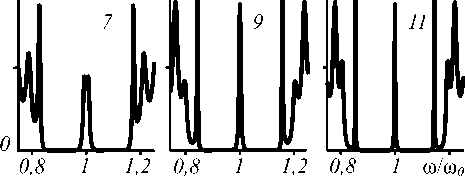
Рис. б. Спектры пропускания для структуры

(I УУМУУМУ с двумя дефектами инверсии, а = 5

Заключение

Проведённый анализ показывает, что в ФКС с дефектом инверсии, состоящей из чередующихся слоёв с различным показателем преломления, в фотонных запрещённых зонах появляются минизоны, для которых коэффициент прохождения близок к единице. Для ФКС с одиночным дефектом и одинаковыми оптическими толщинами соседних слоёв дефектная мода всегда располагается в середине запрещённой зоны. Сдвиг дефекта от середины к краям структуры влияет на интенсивность дефектной моды, которая при этом уменьшается. При произвольных толщинах слоёв дефектная мода смещается от центра запрещённой зоны: при большем показателе преломления на дефекте - в область меньших частот, а при меньшем показателе преломления - в область больших частот. Ширина минизоны пропускания зависит от значения диэлектрической проницаемости на дефекте, числа слоёв и порядка их следования в боковых ФК-зеркалах. Степень локализации поля на дефекте также зависит от диэлектрических проница-емостей слоёв, составляющих дефект. В случае, когда в области дефекта встречаются слои с меньшей диэлектрической проницаемостью, максимум поля наблюдается на границе «нормальной» и инвертированной структуры. В структурах, где дефект составляют слои с большей диэлектрической проницаемостью, на границе «нормальной» и инвертированной структуры наблюдается минимум поля, а максимумы сдвинуты на границы между слоями, составляющими соседние периоды ФКС. Комбинация двух дефектов инверсии позволяет формировать спектральную линию дефектной моды заданного профиля. Слабое поглощение, которое всегда имеет место в структуре, приводит к уменьшению прозрачности структуры вне запрещённых зон, однако внутри этих зон отражательную способность СПС практически не изменяет.

Благодарност и

Работа выполнена при поддержке Министерства образования и науки РФ в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг.