Поляритоны в нанокомпозитах типа металлические наночастицы - диэлектрик

DOI:

Изучение поверхностных электромагнитных волн (ПЭВ) начал А. Зоммерфельдом в 1899 г., описав случай распространения волны вдоль цилиндрического проводника [8]. Математическое описание ПЭВ получили в 1907 г. благодаря работе И. Ценнека по объяснению дальней радиосвязи [3]. Экспериментальное проявление поверхностных электромагнитных волн на границе металла обнаружено Робертом Вудом в 1912 г. в виде решеточных аномалий Вуда, их интерпретация в терминах поверхностных плазмонных поляритонов дана У. Фано (1941) [12]. Впервые выражение для спектра поляритона получили К.Б. Толпыго [10] в 1950 г. и К. Хуанг [13] в 1951 г. в рамках классической теории для двухатомного кубического кристалла в фононной области спектра.

Поверхностные поляритоны (ПП) (англ. surfacepolariton) – это поверхностные электромагнитные волны, распространяющиеся вдоль границы раздела двух разнородных сред и существующие одновременно в них обеих [5; 14].

Согласно представлению макроскопической теории «…при взаимодействии электромагнитной волны с возбуждениями среды возникают связанные волны – поляритонные волны, энергия которых частично состоит из электромагнитной и частично из энергии собственных возбуждений среды» [4].

При удалении от границы двух сред интенсивность таких волн значительно убывает, для линейных сред экспоненциально. На плоской границе раздела сред с одинаковыми физическими свойствами ПП может существовать только при условии, что хотя бы одна из этих сред обладает областью отрицательных значений диэлектрической или магнитной проницаемости (ДП и МП) [1].

Возможность эффективного возбуждения ПЭВ на реальных поверхностях (металлах, полупроводниках, диэлектриках) и влияние ПЭВ на многие фотофизические процессы, протекающие на поверхности исследуемых материалов объясняет важность теоретических и экспериментальных исследований поверхностных поляритонов и их основных характеристик [9].

Среди таких процессов рассеяние света адсорбированными на поверхности частица- ми, генерация второй гармоники при отражении лазерного излучения от металла, изменение поглощения, фотохимические реакции, а также физико-химические процессы, сопровождающие действие на поверхность интенсивного лазерного излучения, в первую очередь образование поверхностных периодических структур [5].

На базе структур, где возможно возбуждение ПП (плазмонных структур), можно создать оптические устройства и сенсоры, которые будут обладать высокой чувствительностью и компактными размерами [12]. Это имеет большое практическое значение для разработок во многих областях. Например, таких как нелинейная оптика, оптическая спектроскопия, микроскопия высокого разрешения и других [9].

Значительный интерес вызывают ме-талл-диэлектрические структуры, в которых возможно возбуждение ПП. В этих структурах концентрация энергии электромагнитного поля (ЭМП) высока вблизи металлической границы [10]. В настоящее время разработки современной науки в области нанотехнологий предоставляют возможность создавать нано-композитные среды с включениями различной формы, размера, концентрации, а также состоящие из различных материалов [2].

Композитные среды с наночаcтицами благородных металлов представляют большой практический интерес при разработке широкого спектра оптических устройств. Линейные и нелинейные оптические свойства таких сред определяются плазмонным резонансом металлических наночастиц и свойствами прозрачной матрицы. Возникновение резонанса диэлектрической проницаемости в нанокомпозите, состоящем из металлических наночаcтиц, взвешенных в прозрачной матрице. Причем положение резонанса зависит как от диэлектрической проницаемости исходных материалов, так и от концентрации наночастиц. Представляет большой интерес, как с прикладной, так и с фундаментальной точки зрения, использование таких нанокомпозитов в качестве материалов фотонных кристаллов.

Расчеты

Рассмотрим задачу: наночаcтицы распределены в матрице случайным образом, но однородно. Будем считать, что наночастицы имеют форму шара, с радиусом в пределах нескольких нанометров, что значительно меньше длины волны и глубины проникновения поля в материал. Диэлектрическую проницаемость металла, из которого изготовлены наночастицы, найдем, используя приближение Друде, в следующем виде:

= - ⁽ “ ’ - = 0 - .у * ( у + i. G ) -            ⁽¹⁾

где s0 - постоянная; юp - плазменная частота; g- -релаксационная постоянная; у = — - нормирован-ωp ная частота; G = — - нормированное затухание. ωp

Для определенности, в качестве металла мы будем использовать серебро и золото. В дальнейших расчетах используются результаты исследования оптических постоянных тонких пленок благородных металлов [6] 1972 г., данные из более новой статьи [11], в которой освещаются результаты измерений комплексной диэлектрической проницаемости металлических пленок различной толщины.

Величины, используемые в формуле 1 для серебра по данным работы [3]:

Е о = 5, ю p = 9эВ, — - = 0,02эВ.

На рисунке 1 представлены зависимости Ree _- (ю) и Ims _- (ю) действительной и мнимой частей комплексной диэлектрической проницаемости наночастиц серебра s _- (ю).

Найдем диэлектрическую проницаемость нанокомпозита smix(ю) в следующем виде:

E_d * ( 1 + 2 * x )

E mix ( ю )                                  (2)

1 - x

На рисунке 2 представлены зависимости Res_mix(ю) и Ims_mix(ю), при s d = 2,56,

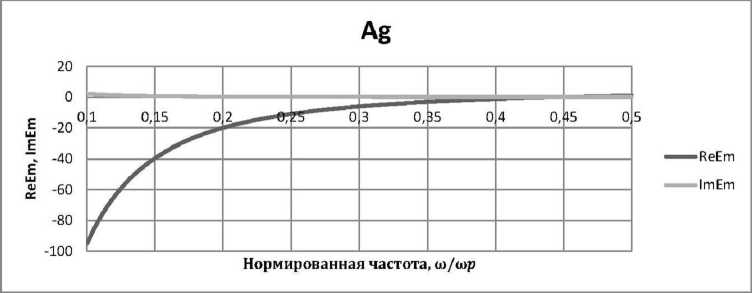
Рис. 1. Функции Re s _- ( ю ) и Im s _- ( ю ) для серебряных наночастиц

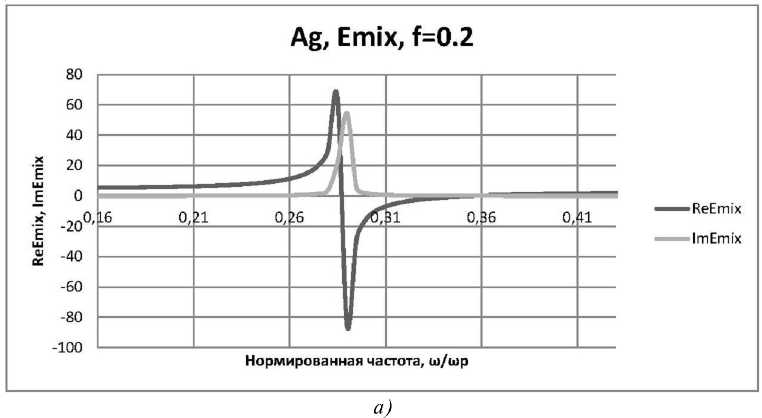
Рис. 2. Функции Re s _- ( ю ) и Im s _- ( ю ) для серебряных наночастиц, взвешенных в прозрачной матрице: а) при f = 0,2, е d = 2,56

f = 0,2 , f = 0,35 , f = 0,4 , f = 0,5 . Кривые на рисунке 2, как видно, имеют резонансный характер. Найдем точки, в которых e mix (o) превращается в ноль, пренебрегая малым g_m .

1 - f

£ 0 + ² * ^£ d ^{- f} * ( S 0 ^{- £} d )

ω10

= ® р

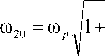
^£0 * ^{( s} 0 ^{+ 2} * ^S d ^{- f} * ^{( s} 0 ^{- S} d ))

^£ d * ( £ 0 + 2 * £ d + 2 * ^f * ( ^£0 ^- £ d ))

б)

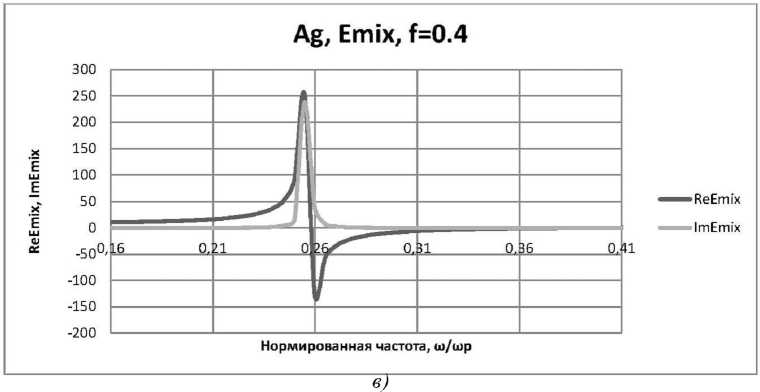
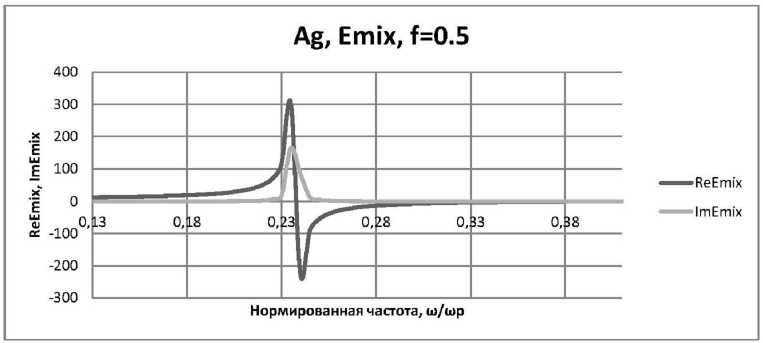
г)

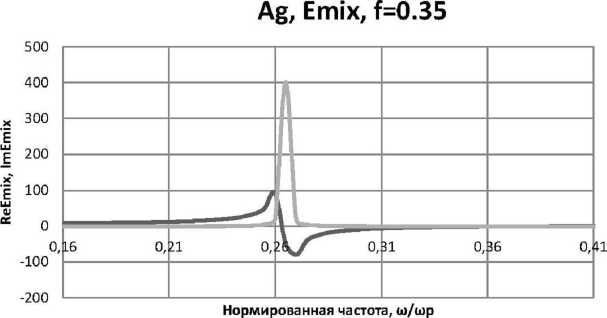
Рис. 2. Окончание:

б) при f = 0,35 , £ _d = 2,56; в) при f = 0,4, £ _d = 2,56; г) при f = 0,5, £ d = 2,56

^Ю10 = 0,288 и ^ = 0,355, при f = 0,2, е d = 2,56; ω _p         ω _p

^ = 0,265 и ^2° = 0,379, при f = 0,35, е d = 2,56; ω _p         ω _p

^ = 0,256 и ^ = 0,386, при f = 0,4, е d = 2,56; ω _p         ω _p

• ■^ = 0,237 и ^ = 0,399, при f = 0,5, е d = 2,56. ω _p         ω _p

  В отличие от работы [7], в нашем случае максимальные значения Ree mix (o)max = 64,95912, Ims mix ( ю ) max = 54,47379 при f = 0,2 , 'sd = 2,56 , что меньше тех же показателей в ранее указанной работе.

В области частот ю10 > ю > ю20 наблюдается отрицательная действительная часть диэлек- трической проницаемости (ДП) нанокомпозита. В этих частотах вдоль границы раздела возможно распространение поверхностных волн – поверхностных поляритонов. Следовательно, нанокомпозит подобен металлу в этой области.

Далее найдены дисперсионные зависимости для действительной и мнимой частей диэлектрической проницаемости композитной среды, представленной в виде наночастиц серебра, распределенные случайно, но однородно в матрице диэлектрика (рис. 3, 4).

На рисунке 5 представлены зависимос- ое е 1 ( х ) и е ₂ ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости наночастиц золота s m ( X ) на основе данных из работы [6]. Толщина пленки металла в

Ag, ReNII

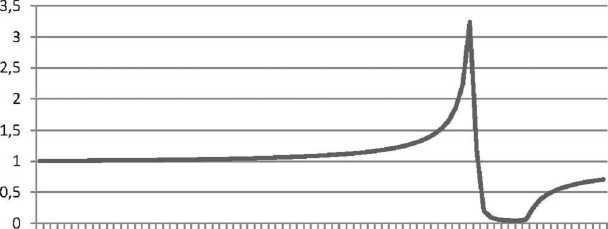
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 6164 67 70 73 76 79 ш/шр

Рис. 3. Дисперсионная кривая для действительной части диэлектрической проницаемости нанокомпозита: наночастицы серебра, распределенные случайным образом в прозрачной матрице

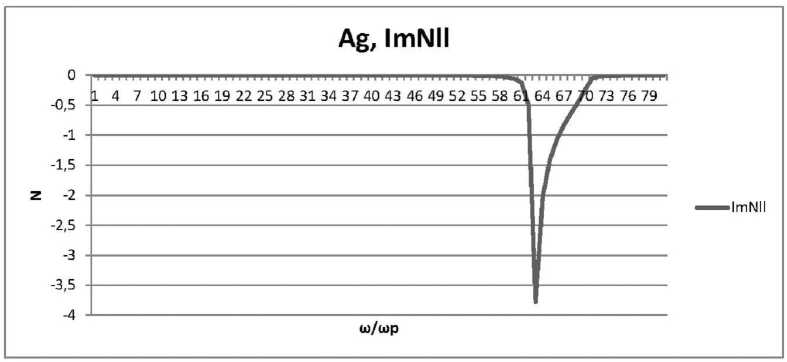
Рис. 4. Дисперсионная кривая для мнимой части диэлектрической проницаемости нанокомпозита: наночастицы серебра, распределенные случайным образом в прозрачной матрице этом исследовании равна от 18,5 до 50 нм с погрешностью измерений в 0,2 нм.

На рисунке 6, 7 представлены зависимости £ 1 ( X ) и £ 2 ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости наночастиц золота £ m ( X ) на основе данных из работы [11]. Толщина пленок в этом исследовании равна 25 нм, 53 нм и 117 нм.

Затем, для того, чтобы найти диэлектрическую проницаемость нанокомпозита £ mix ( ю ) используем формулу Максвелла-Гарнета [15]:

^£ mix ^{( ю )- £} d = f ^£ m ^{( ю )- £} d

£mix (®)+ 2£d     £m (®)+ 2£d где ю - частота излучения; f- относительный объем занимаемый наночастицами; εd – диэлектрическая постоянная матрицы, в которую погружаются наночастицы (£d = 2,56), £m (ю) - диэлектрическая проницаемость металла, из которого изготовлены наночастицы.

Подставим (1) в (5) и найдем £ mix ( ю ) в следующем виде:

	=. . ( » ) = ^^ , 1 - x	(6)
где	f ( £ m - £ d ) x =              . £ m + 2£ d	(7)

Au

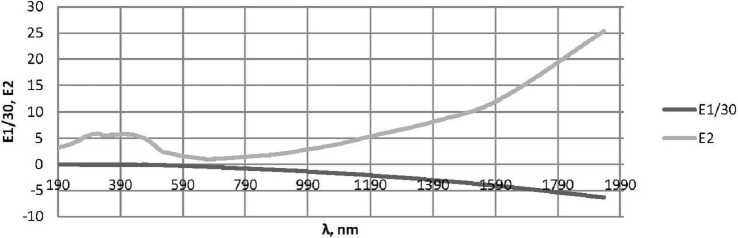
Рис. 5. Зависимости £ 1 ( X ) и _£ 2 ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости наночастиц золота £ _m ( X )

а)

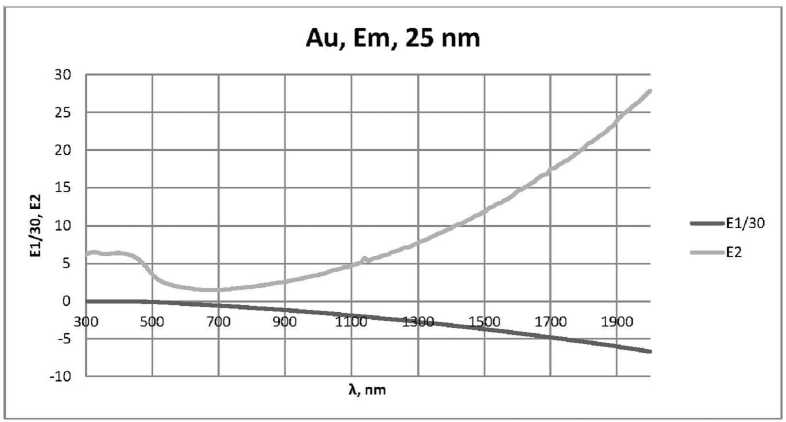
Рис. 6. Зависимости £ 1 ( X ) и _£ 2 ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости наночастиц золота £ _m ( X ) для пленок толщиной:

а) 25 нм

				Au,	Em, 53 nm
О' 10 5* s 0 3( -5
	10________5i	Ю______71	10_______9!	Ю    11			ад 17	Э0_____19	—Е1/30 ^—Е2 00
				К, nm

б)

^—El/30

Е2

в)

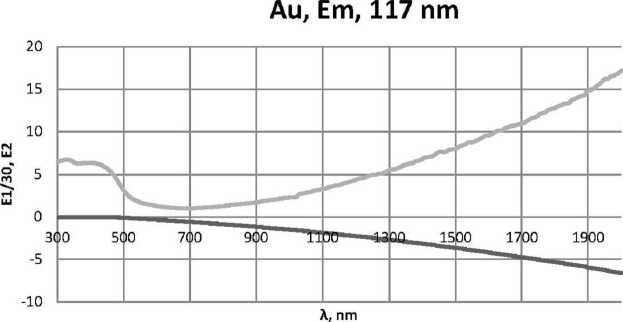
Рис. 6. Окончание:

б) 53 нм; в) 117 нм

Au, Em

^— El/30, 25 nm

^—El/30,53 nm

^—El/30,117 nm

E2, 25 nm

E2, 53 nm

E2,117nm

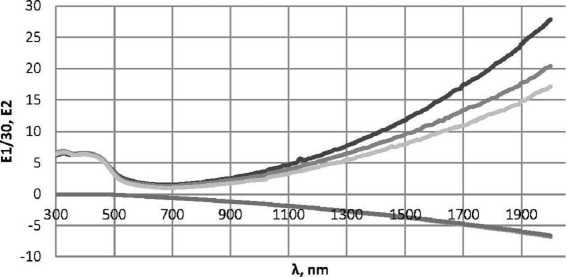
Рис. 7. Зависимости £ 1 ( X ) и £ 2 ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости наночастиц золота £ m ( X ) для пленок с толщинами 25 нм, 53 нм и 117 нм

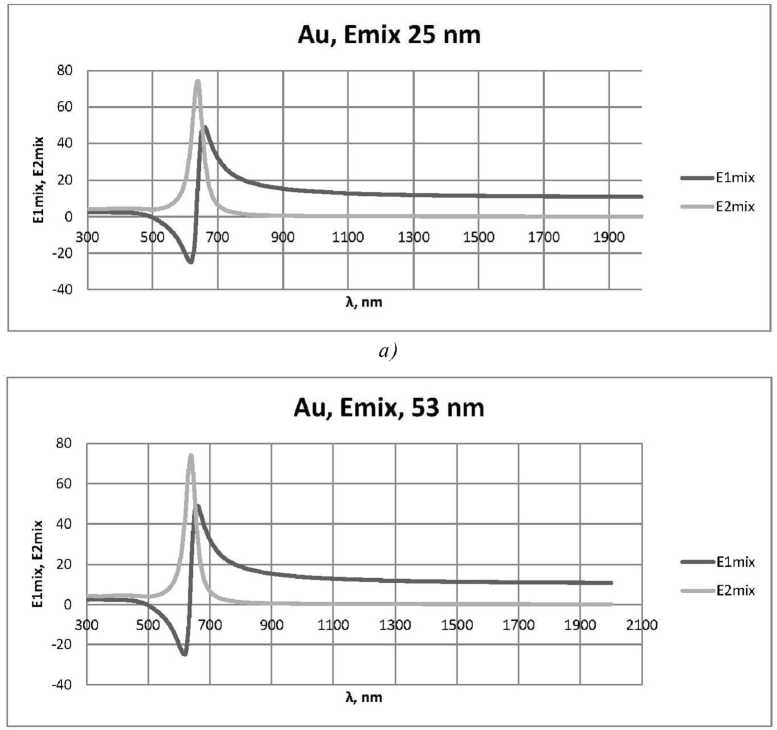
Зависимости 81 mix (X) и 82m/x (X) Действительной и мнимой частей комплексной диэлектрической проницаемости нанокомпо- зита с частицами золота 8mix(X) для пленок различной толщины показаны на рисунке 8.

б)

в)

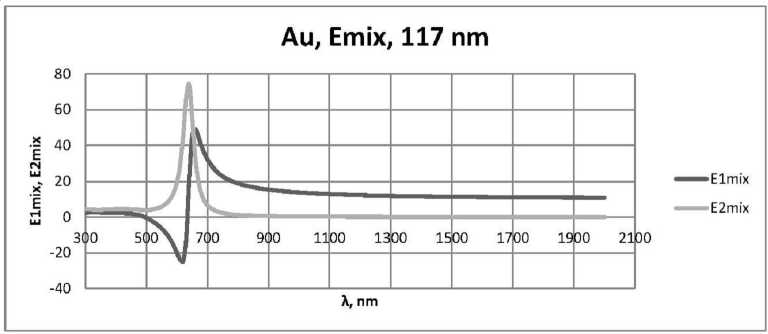
Рис. 8. Зависимости 8 1 _mix ( X ) и 8 2 _mix ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости нанокомпозита с частицами золота 8 _mix ( X ) для пленок толщиной:

• а) 25 нм; б) 53 нм; в) 117 нм, при 8 d = 2,56 , f = 0,5

Кривые на рисунке 9, как видно, имеют резонансный характер (вид кривых аналогичен случаю ионного материала).

Функция е mix ( ю ) в интервале [ ю₁₀,ю₂₀ ] отрицательна. Следовательно, нанокомпозит подобен металлу в этой области. В области частот ю₁₀ >  ю >  ю₂₀ наблюдается отрицательная действительная часть ДП нанокомпозита. В этих частотах вдоль границы раздела возможно распространение поверхностных волн – поверхностных поляритонов. Варьирование материалами структуры, размером и концентрацией наночастиц открывает широкие возможности для управления оптическими свойствами нанокомпозитной среды (НКС) и практического их применения.

Дисперсионное уравнение для поверхностного поляритона на границе нанокомпозит-воздух в случае s -поляризации будет иметь вид:

ks = k 0 ns k 0 =ю/c0

Показатель преломления нанокомпозита в случае s-поляризации.

ns

^е mix ^{( ю ) е}0

^е mix ^{( ю )+ е}0

где E q - диэлектрическая проницаемость воздуха ( e₀ = 1).

На рисунке 10 представлены графики зависимости n_{s 1} и n_{s 2} действительной и мнимой частей комплексного показателя прелом-

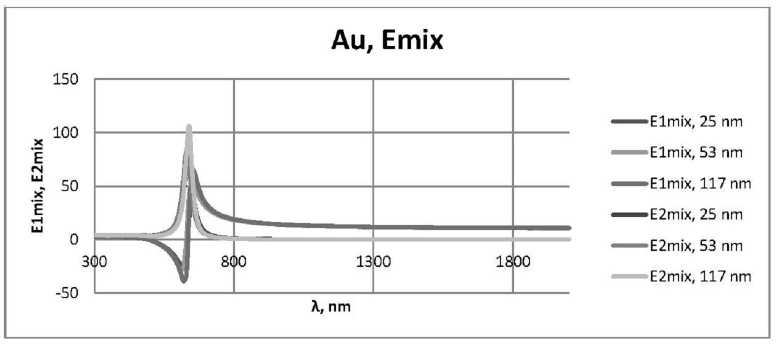
Рис. 9. Зависимости е_{1 mix} ( X ) и е_{2 mix} ( X ) действительной и мнимой частей комплексной диэлектрической проницаемости нанокомпозита с частицами золота е _mix ( X ) для пленок с толщинами 25 нм, 53 нм, 117 нм, при е d = 2,56, f = 0,5

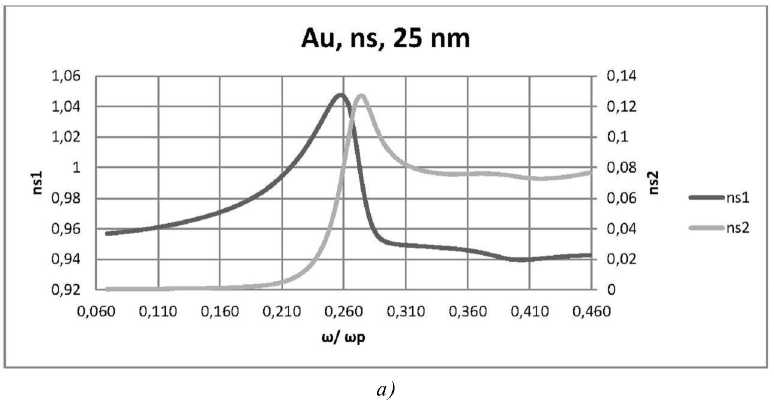
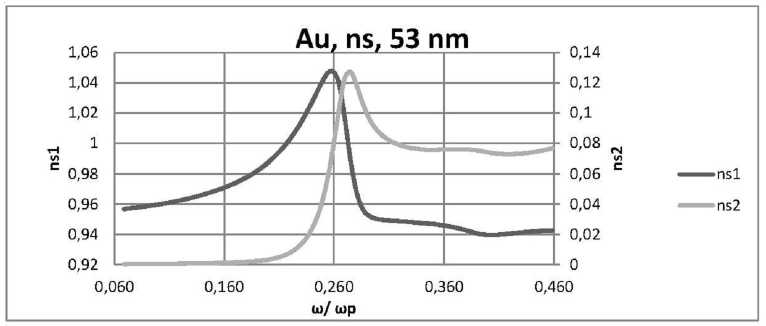
Рис. 10. Зависимости n_{s 1} и n_{s 2} действительной и мнимой частей комплексного показателя преломления нанокомпозита n от нормированной частоты to / to p в случае s -поляризации для пленок толщиной: а) 25 нм;

ления нанокомпозита соответственно от нормированной частоты to / to p для случая s -поляризации при е d = 2,56 , f = 0,5 .

Таким образом, как можно видеть из графиков на рисунках 10–18, варьирование материалами структуры, размером и концентрацией наночастиц открывает широкие возможности для изменения показателя преломления нанокомпо-зитных сред и практического их применения.

Используя формулу 8 для дисперсионного уравнения для поверхностного поляритона на границе нанокомпозит-воздух получим следующие результаты.

Выводы

В работе были изучены объемные и поверхностные поляритоны в наноматериалах. Поляритонные модели позволяют описать динамику генерации и распространения линейных и нелинейных волн в различных средах в широком частотном диапазоне. На основе поляритонных моделей удается наиболее полно описать физические механизмы взаимодействия электромагнитного излучения со средой.

Изучение поверхностных поляритонов и их основных характеристик на сегодняшний день представляют важную задачу для создания оптических устройств и сенсоров, которые будут обладать высокой чувствительностью и компактными размерами, для создания оптических линий передачи данных с наноразмерными устройствами генерации и для управления излучением.

Были рассчитаны действительные и мнимые части диэлектрической проницаемости для поляритонов в нанокомпозите. Найдены значения показателя преломления композитного наноматериала при различных концентрациях металлических наночастиц в матрице диэлектрика. Кроме того построены дисперсионные кривые для нахождения поляритонов в нанокомпозитах типа: наночастицы благородных металлов, распределенные случайным образом в прозрачной матрице.

б)

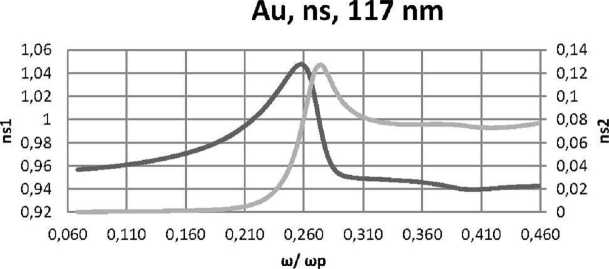
в)

Рис. 10. Окончание:

б) 53 нм; в) 117 нм, при е d = 2,56, f = 0,5

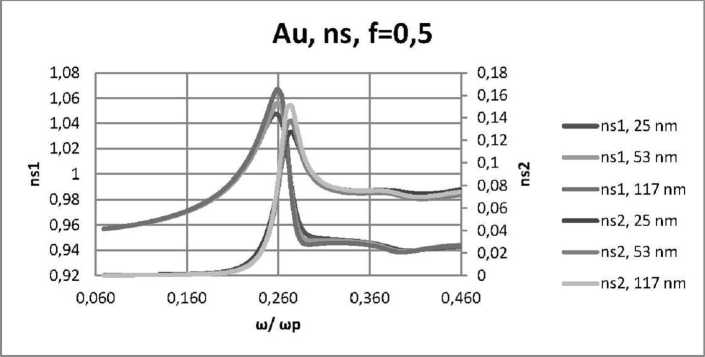
Рис. 11. Зависимости ns1 и ns2 действительной и мнимой частей комплексного показателя преломления нанокомпозита n от нормированной частоты ю/юp в случае 5-поляризации для пленок толщинами 25 нм, 53 нм, 117 нм, при еd = 2,56, f = 0,5

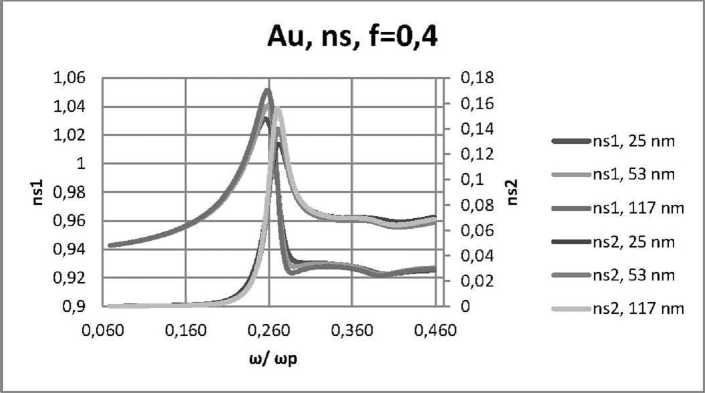
Рис. 12. Зависимости ns1 и ns2 действительной и мнимой частей комплексного показателя преломления нанокомпозита n от нормированной частоты ю/юp в случае 5-поляризации для пленок толщинами 25 нм, 53 нм, 117 нм, при еd = 2,56, f = 0,4

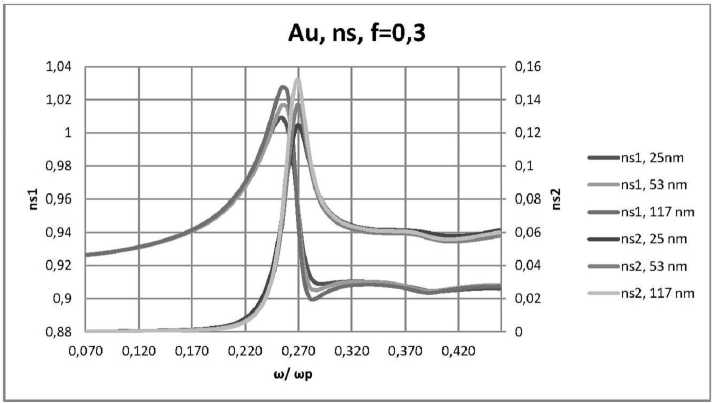
Рис. 13. Зависимости ns1 и ns2 действительной и мнимой частей комплексного показателя преломления нанокомпозита n от нормированной частоты ю/юp в случае 5-поляризации для пленок толщинами 25 нм, 53 нм, 117 нм, при еd = 2,56, f = 0,3

ш/ шр

^^—nsl, 25 nm

nsl, 53 nm

nsl, 117 nm

ns2, 25 nm

^^—ns2, 53 nm

ns2,117 nm

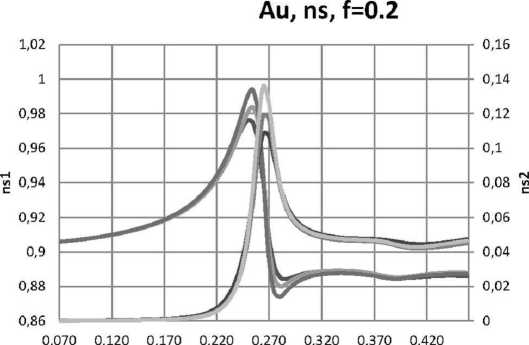
Рис. 14. Зависимости n_{s 1} и n_{s 2} действительной и мнимой частей комплексного показателя преломления нанокомпозита n от нормированной частоты ю / ю p в случае 5 -поляризации для пленок толщинами 25 нм, 53 нм, 117 нм, при е d = 2,56, ' f = 0,2

Au, ks, f=0,5

to/ top

^^—ksl, 25 nm

ksl, 53 nm

ksl, 117 nm

ks2, 25 nm

ks2, 53 nm

ks2,117 nm

Рис. 15. Дисперсионные кривые для действительной и мнимой частей диэлектрической проницаемости нанокомпозита: наночастицы золота, распределенные случайным образом в прозрачной матрице для пленок толщинами 25 нм, 53 нм, 117 нм, при е d = 2,56, / = 0,5

—ksl, 25 nm

ksl, 53 nm

ksl, 117 nm

ks2, 25 nm

ks2, 53 nm

ks2,117 nm

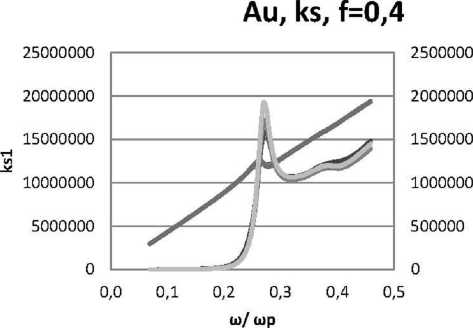
Рис. 16. Дисперсионные кривые для действительной и мнимой частей диэлектрической проницаемости нанокомпозита: наночастицы золота, распределенные случайным образом в прозрачной матрице для пленок толщинамиа 25 нм, 53 нм, 117 нм, при е d = 2,56, f = 0,4

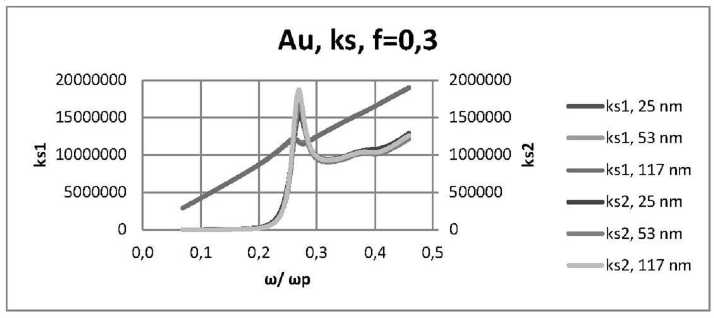
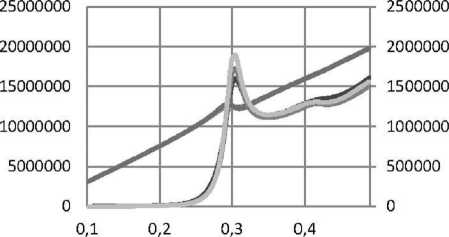
Рис. 17. Дисперсионные кривые длядействительной и мнимой частей диэлектрической проницаемости нанокомпозита: наночастицы золота, распределенные случайным образом в прозрачной матрице для пленок толщинами 25 нм, 53 нм, 117 нм, при ε _d = 2,56, f = 0,3

—ksl, 25 nm

----ksl, 53 nm

^— ks, 117 nm

^—ks2, 25 nm

— ks2, 53 nm ks2,117 nm

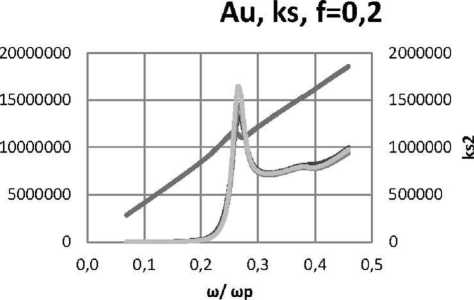
Рис. 18. Дисперсионные кривые для действительной и мнимой частей диэлектрической проницаемости нанокомпозита: наночастицы золота, распределенные случайным образом в прозрачной матрице для пленок толщинами 25 нм, 53 нм, 117 нм, при ε _d = 2,56, f = 0,2