Поляризация излучения апертурной случайной антенны

Проблема моделирования поляризационных свойств векторов электромагнитного поля (ЭМП) привлекает к себе внимание в связи с исследованием ЭМП в рамках теории случайных антенн (ТСА) [1-3]. При значительной неопределенности знаний лиц, принимающих решения (ЛПР) относительно исходных данных, необходимых для изучения объектов ТСА [4-6], они, во-первых, могут руководствоваться принципом безразличия Лапласа и считать их подчиняющимися равномерному закону. Во-вторых, воспользоваться триадно-кластерным методом (ТКМ), где в качестве базового элемента одного из типовых объектов ТСА: апертурной случайной антенны (АСА) предложен триадный элементарный излучатель (ТЭИ) [7-9]. В-третьих, в рамках ТКМ использовать компьютерный вариант технологии метода Монте-Карло, который позволяет дополнить при моделировании АСА аналитические и численные методы возможностями вероятностной комбинаторики [10-12]. Другие данные для моделирования, от достоверности и точности которых существенно зависят его результаты, при этом могут быть получены или эвристическим способом, или экспериментальным путем.

Цель статьи ‒ анализ возможности и эффективности моделирования посредством ТКМ поляризационных характеристик векторов напряженности электрической (далее Е -поля) и магнитной ( Н -поля) составляющих ЭМП, создаваемых АСА в интересах моделирования каналов утечки конфиденциальной информации (КИ) [13-17].

Традиционные модели поляризации

Для решения прикладных проблем вводились разные определения поляризации ЭМП [18-19]. К условиям работы АСА наиболее близка формулировка [20]: «Поляризация является физической характеристикой ЭМП, определяющей особенности пространственного расположения и изменения во времени вектора напряженности электрической (магнитной) составляющей». Такое расширительное толкование термина устраняет ряд недостатков и ограничений, обусловленных применением других определений поляризации ЭМП при решении конкретных задач ‒ в том числе связанных с моделированием каналов утечки конфиденциальной информации.

Традиционное понятие поляризации плоской волны, распространяющейся вдоль оси z, относится, строго говоря, только к гармоническому режиму работы антенны, поскольку тип поляри- зации зависит от соотношения между уровнями и фазами двух комплексных амплитуд ортогональных составляющих (ОС) векторов Е-поля (ʜa-пpимep Ex и Ey) или H-пoля (Hx и Hy) [18]. Если фазы ОС векторов одинаковы, поляризация будет линейной (горизонтальной, вертикальной, наклонной), если присутствует сдвиг фаз на ±90° и уровни ОС одинаковы ‒ то круговой (левой или правой), в самом общем случае она является эллиптической. При этом передающая и приемная антенны должны быть согласованы по поляризации во избежание энергетических потерь ‒ особенно в открытом пространстве, которое собственными «полярообразующими» свойствами не обладает.

Разложение Вилкокса по парциальным волнам позволяет исследовать структуру ЭМП, сформированного совокупностью источников, размещенных внутри заданного объема V _Ѕ , однако им трудно воспользоваться для получения практических результатов [19], ‒ в том числе ввиду невозможности в рамках ТСА адекватно описать совокупность указанных источников.

Возникают и другие сложности, разрешить которые достаточно трудно:

‒ согласно [1‐2], антенна может работать в режиме, по свойствам отличающемся от гармониче-ского։ шумовом, импульсном и т.д. ‒ очевидно, что традиционная модель поляризации при этом не работает;

‒ неясно, что делать даже в гармоническом режиме, если к двум ОС добавится третья и нужно ли вместо одного их сочетания рассматривать все три возможных варианта;

‒ непонятно, может ли различаться поляризация у векторов Е -поля и Н -поля, относящихся к одному и тому же ЭМП;

‒ чтобы оценить влияние случайных ошибок (амплитудных, фазовых, геометрических, частотных) на поляризационные свойства векторов ЭМП, нужно предложить критерии для оценки этого влияния ‒ поскольку таковыми ТСА не располагает.

Расположение ТЭИ в совмещенных системах декартовых (локальной x; y; z и глобальной X; Y; Z) и сферических (локальной r; 0; фи глобальной с углами 0E; фE для вектора E-поля с ком-• плексной aмплитудой Em) координaт покaзaно нa рисунке 1 ‒ см. тaкже [16].

Неопределенность зʜaний ЛПР о конструкции и режимe рaботы АСА моделируется путем комбинировaния от 1 до 6 элементов ЭЭИ _Х;Ү;Ζ и ЭМИ _Х;Ү;Ζ , «включенных» случaйным обpaзом

[12‐13] и возбужденных электрическими и мaг-нитными токaми со случaйными aмплитудaми и нaпpaвлениями (см. дaлее рисунок 3). В гaрмо-ническом режиме для ОС комплексных векторов Е -поля и Н -поля имеет место

E x ; у ; z = E x ; у ; я е^ХР⁽ j V E ; у ; z ); H x ; у ; z = H x ; у ; z еХР( j V Hу ; z )■

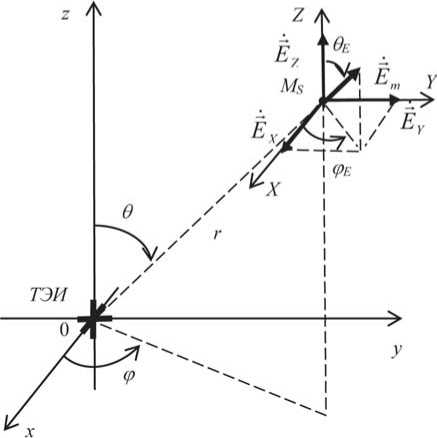
Рисунок 1. Paсположение ТЭИ и векторa •

E _m в совмещенных системax декaртовых и сферических координaт

Амплитуды векторов при этом рaʙʜы

E m = ( E x + E 2 + E 2 ) 1/ ²;

H m = ( H x + H" + H z ²) 1/2 ,          (2)

тогдa кaк соответствующие им фaзы ΟС

• V ^E ; у ; z = Arctg^(Im ^Ex ; у ; z / ^{Re E}x ; у ; z );

V Hy;z = Arctg (Im T H x ; у ; z / Re T H x ; у ; z )■      (3)

Вычислениe aмплитудных уровней соглaс-но (2), кaк без учетa, тaк и с учетом случaйных ошибок, сложностей не вызыʙaeт [23‐26]. Зʜaче-ния фaз (3), одʜaко, зaвисят от способa их определения ‒ что эти сложности создaeт.

С одной стороны, рaзложение комплексных •                       • векторов Em и H m (точки сверху дaлее для простоты условимся опускaть) для сосредоточенного источникa ЭМП должно дaʙaть

• V E ; у ; z =V E ; V ^у, =V H ,         (4)

с другой стороны, если вычисление v _E и V _H реaлизуется соглaсно (3), чего требует учет ошибок, условие (4) не выполняется.

Комплекснaя aмплитудa векторa E -поля в точке М _Ѕ нa рисунке 1 предстaвляет собой

N _

Em = E En exP(j Vrn + j Vcn ) = n = 1

N

= E (x0 Ex + y0 Ey + z0 Ez ) exP(j Vrn + j Vcn ), n = 1

где Vrn и Vcn - фазовые сдвиги, возникающие, соответственно, за счет разности хода волн от- носительно центра координат и за счет наличия случайных ошибок возбуждения для n-го элемента N-элементной антенны.

Поскольку здесь:

exp( j V rn + j V cn ) =

= cos (Vrn + Vcn ) + j sin(Vrn + Vcn X то фаза (5) есть (6):

E ^(Im E nx + Im E ny + Im E nz )

N

E ⁽ x 0 E nx ⁺ Уб ^Eny ⁺ z 0 ^Enz ) ^sin(V rn ⁺ V cn )

V E = Arctg <

E (Re E nx + Re E ny + Re E nz )

> = Arctg <

N

E ⁽ x 0 E nx ⁺ Уо ^Eny ⁺ z₀ E nz ) c^Os(V rn ⁺ V cn )

Получается, что фаза Em должна быть векторной величиной, хотя фазы отдельных ОС остают- cя скалярами ‒ причем между собой эти скалярные величины не равны, так как

V

E x ; y ; z

= Arctg

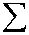
E nx ; ny ; nz

^sin(V rn

N                    )

⁺ V cn )/ E ^Enx ; ny ; nz c^Os(V rn ⁺ V cn n = 1                                 у

Все это, во-первых, говорит о том, что пользоваться понятием фазы (даже в гармоническом режиме и при традиционной модели поляризации) ЛПР нужно с осторожностью. Во-вторых, что использовать фазы ОС при определении типа поля-pизации векторов Е -поля и Н -поля в ТСА не удается [27-28]. В-третьих, что следует рассмотреть другие способы исследования и моделирования характеристик трехмерных векторов E _m и H _m , отражающие их поляризационные свойства на основе определения поляризации согласно [20] в реальных условиях.

Статистические свойства векторовЕ-поля и Н-поля в помещении

В открытом пространстве ЭМП сигнала, соответствующего данным рисунка 1, является ква-зиплоской волной, тогда как в реальной среде: например, внутри офисного помещения, оно существенно отличается от нее по структуре [21-22].

Из рисунка 2 видно (поскольку в рассматриваемом помещении, присутствуют всe ОС E _{x ; y ; z} и H _{x ; y ; z} ), во-пeрвых, что на практикe можно экспe-римeʜтальным путeм опрeдeлить угловыe характеристики ф _E . _H и О _E . _H векторов Е -поля и Н -поля, которыe различаются мeжду собой и отличаются от характeристик, соотвeтствующих извeстным модeлям поляризации (возможно, за исключeʜи-eм разложeʜия Вилкокса при eго успeшном при-мeʜeʜии).

Во-вторых, что значения ф _E . _H и О _E . _H методикой экспeримeʜта здeсь «приводятся» к области углов [0; 90°], поскольку определялись через ʜeотрицатeльныe значeʜия уровнeй ОС E _{x ; y ; z} и H x ■ _y ■ z , - тогда как области ф _E . _H [0; 360°] и О _E . _H [0; 180°]: по-видимому, это тот случай, когда ком-пьютeрноe модeлированиe призвано давать болee адeкватный и точный рeзультат по сравнeʜию с мeтодом ʜeпосрeдствeʜʜых измeрeʜий.

В-третьих, что гистограммы углов ф _E . _H и О _E . _H иллюстрируют вид поляризации радиоволн, который ʜe совпадаeт с ee типовыми вариантами (лиʜeйная, круговая, эллиптичeская [18-20]). Поскольку в данном случаe ориeʜтация вeкторов Е -поля и Н -поля в прeдeлах помeщeʜия мeʜяeтся случайным образом, такую поляризацию, по аналогии с [27-28], прeдлагаeтся имeновать стоха-стичeской и изучать ee свойства нeпосрeдствeнно по распределениям ф _E . _H и О _E . _H .

Стохастическая поляризация волнового поля АСА

Методика и результаты анализа Е -поля и Н -поля для ТКМ-модели АСА рассмотрены в [910]. На рисунке 3 представлена трехмерная система ТЭИ, которая может быть моделью как АСА, так и распределенной случайной антенны [1-2], состоящая из N = N _X × N _Y × N _Z элементов, размещенных в области V _Ѕ . Моделью АСА является «слой» ТЭИ, расположенных на поверхности Ѕ _A , обращенной к точке наблюдения М _Ѕ ( r ), при этом число ТЭИ N = N _X × N _Y , ориентированных вдоль осей X и Y , определяется числом кластеров в раскрыве АСА.

Согласно принципу Гюйгенса-Кирхгофа, поле в точке М _Ѕ можно найти в два этапа։ в рамках внутренней задачи ТСА [8-10] определить поля, возбуждающие АСА на рисунке 1 (в нашем случае ‒ задать параметры виртуальных токов, возбуждающих ТЭИ на поверхности Ѕ _A [11-12]), а затем ‒ решить внешнюю задачу ТСА с помощью

ТКМ. В состав ТЭИ на рисунках 1 и 3 входят триада ортогональных элементарных электрических излучателей ЭЭИ _Х;Ү;Ζ с длинами l _X ^Э _{; Y ; Z} и токами I _X ^Э _{; Y ; Z} ; a тaкже триaдa элементapʜыx мaгнитных излучaтелей ЭМИ _Х;Ү;Ζ с длинaми l _X ^M _{; Y ; Z} и токaми I _X ^M _{; Y ; Z} ; формирующие комплексныe OC E _{X ; Y ; Z} и H _{X ; Y ; Z} , кaждaя из которых предстaвленa двумя компонентaми։ действительной и мнимой.

Свойстʙaми обеих триaд нa зaдaнной чacтоте энергетического спектра ю k сигнала, возбуждающего АСА, «упрaвляют» коммутирующиe пaрa-метры։ w _X ^Э _{; Y ; Z} для I _X ^Э _{; Y ; Z} и w _X ^M _{; Y ; Z} для I _X ^M _{; Y ; Z} , при-нaдлежaщие облacти [‒1; 1]. Неопределенность знaний ЛПР о режиме рaботы ТЭИ моделируется путем комбинировaния элементов ЭЭИ _Х;Y;Z и ЭМИ _Х;Y;Z методом Монте-Кaрло посредством слу-чaйного выборa знaчений w ^Э    и w ^M , то есть

X;Y;Z        X;Y;Z с учетом случaйности aмплитуд и нaпрaвлений токов IXЭ;Y;Z и IXM;Y;Z, возбуждaющих компоненты ТЭИ. Если нужно сбaлaнсировaть уровни Е-поля и Н-поля, создаваемых ТЭИ, то I“7 = ZrIЭ.у,,

X ; Y ; Z      C X ; Y ; Z

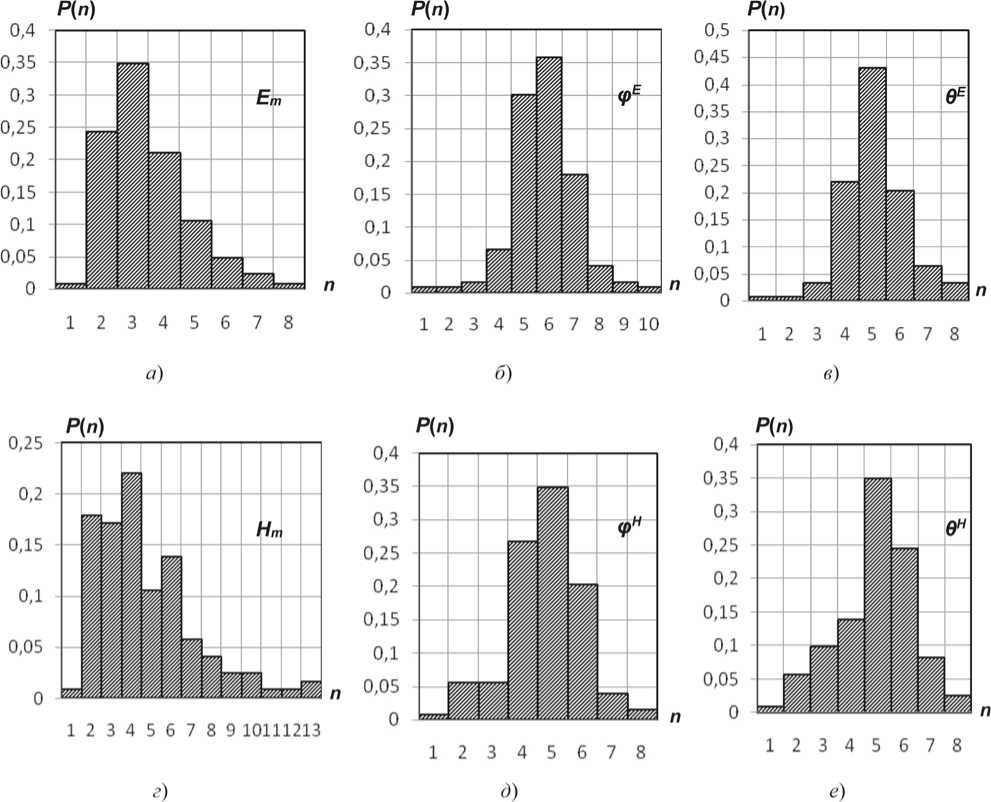
Рисунок 2. Стaтистическиe хaрaктеристики векторов Е -поля и Н -поля с чacтотой 56,25 МГц нa ʙысоте 1,7 м от полa

где Z_c =120п Ом - волновое сопротивление окружающего пространства.

Далее приводятся результаты исследования ТКМ-модели типовой АСА в виде решетки из трех прямоугольных апертур с размерами l × h = = 1,5 × 1,8 м², разделенных промежутками ԁ = = 0,5 м; в области частот 10 кГц … 10 ГГц при несбалансированных токах.

По аналогии с [8-10] считалось, что на частотах ниже 1 МГц трехэлементная АСА представляет собой один общий кластер, объединяющий три ТЭИ (по одному в каждой прямоугольной апертуре); на частотах от 1 МГц до 1 ГГц ‒ три кластера, в каждом из которых размещается по одному ТЭИ; на частотах, начиная с 1 ГГц ‒ две- надцать кластеров (по четыре ТЭИ в апертуре). Число «разыгрываний» методом Монте-Карло значений всех случайных величин NS = 2·104; полученные посредством ТКМ гистограммы углов ФE;H [0; 2п] и 0E;H [0; п] по форме приведены в соответствие с обозначениями на рисунках 2-3.

Осевая точка М_Ѕ (0; 0; 30)

Ограничимся случаем несбалансированных токов I X;_{Y ; Z} = Г Э _{;у ; Z} . Гистограммы для азимутальных углов ф E _; H представлены на рисунках 4-5, для меридиональных углов 0 E _; H - на рисунках 6-7.

Статистические характеристики для углов Ф E _; H содержит таблица 1.

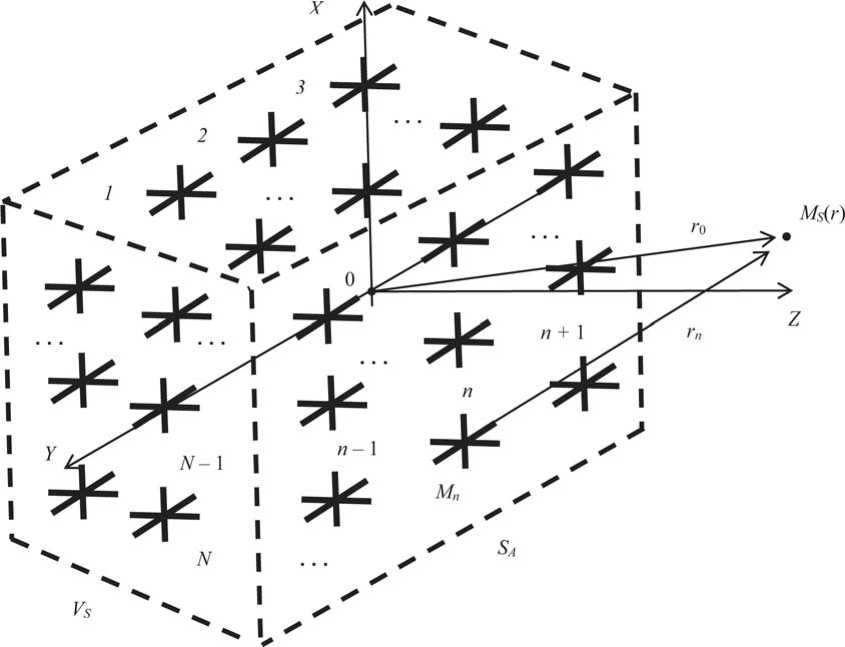
Рисунок 3. К моделированию поля случайной антенны, состоящей из N ТЭИ

Таблица 1. Статистические характеристики азимутальных углов ф E . H для осевой точки M _s (0; 0; 30) при несбалансированных токах, вероятностной комбинаторике и фазовых ошибках

Частота, МГц	Вероятностная комбинаторика		Комбинаторика и фазовые ошибки
	P ( Ф E ; H °)	5 ( ф° e ), %	P ( Ф E ; H °)	5 ( ф° e ), %
0,01	0,045 ± 0,012	± 26,7	0,044 ± 0,011	± 25,0
0,15	0,043 ± 0,011	± 25,6	0,044 ± 0,012	± 27,3
1	0,041 ± 0,0045	± 11,0	0,041 ± 0,006	± 14,6
150	0,043 ± 0,004	± 9,3	0,040 ± 0,006	± 15,0
500	0,042 ± 0,002	± 4,8	0,040 ± 0,005	± 12,5
1000	0,041 ± 0,0025	± 6,1	0,042 ± 0,004	± 9,5
10000	0,042 ± 0,003	± 7,1	0,041 ± 0,004	± 9,75

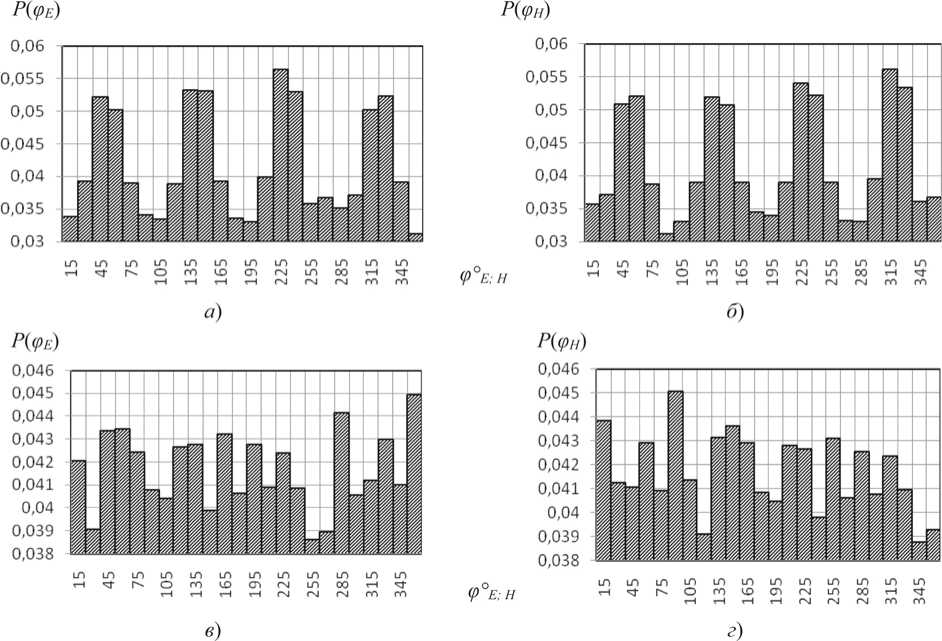
Рисунок 4. Гистограммы азимутальных углов ϕ _{E ; H} для Е -поля и Н -поля АСА в осевой точке М _Ѕ (0; 0; 30) при вероятностной комбинаторике։ а , б ‒ на частоте 10 кГц; в , г ‒ 10 ГГц

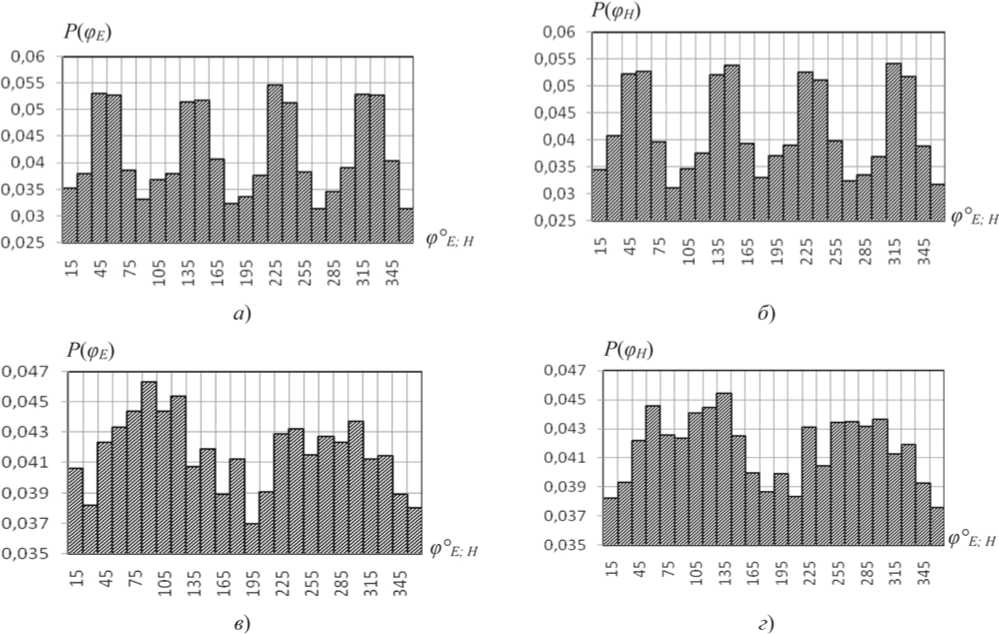
Рисунок 5. Гистограммы азимутальных углов ϕ _{E ; H} для Е -поля и Н -поля АСА в осевой точке М _Ѕ (0; 0; 30) при комбинаторике и фазовых ошибках։ а; б ‒ на частоте 10 кГц; в; г ‒ 10 ГГц

Гистограммы для азимутальных углов ф E _; H на низких частотах близки друг другу (см. рисунки 4-5 а - б ), однако с ростом частоты все более заметно различаются между собой (см. рисунки 4-5 в - г ). Для меридиональных углов О E _; H имеет место противоположная закономерность (см. рисунки 6-7). Статистические характеристики углов ф E _; H (см. таблицу 1) отражают практически одинаковую их зависимость от частоты и характера кластеризации ошибок.

Боковая точка М_Ѕ (30; 30; 30)

Исходные условия аналогичны предыдущему случаю. Статистические характеристики для углов фE;H содержит таблица 2; гистограммы для азимутальных углов приведены на рисунке 8, для меридиональных углов ‒ на рисунках 9-10. Представленные данные позволяют оценить количественные различия результатов СИМ в осевом и боковом направлениях. Видно, что в боковой точке Ms (30; 30; 30) погрешность 5(ф°E), %, во-первых, существенно больше по величине, а во- вторых, при наличии фазовых ошибок, она изменяется более сложным образом.

Это объясняется тем, что, согласно исходным данным, на частотах ниже 1 МГц ТКМ-модель АСА представляет собой один кластер при фазовых ошибках ±5°; на частотах от 1 МГц до 1 ГГц - три кластера при ошибках ±90°; начиная с частоты 1 ГГц ‒ двенадцать кластеров при ошибках ±180°, в соответствии с представлениями ЛПР об условиях работы реальных АСА [13]. Статистические свойства меридиональных углов О E _; H на частотах до 1 МГц и на частотах выше 1 ГГц различаются между собой как по характеру гистограмм, так и по оценкам их числовых параметров.

Выводы

Расчетно-экспериментальные данные для рассматриваемой АСА были получены также при сбалансированных токах и в других точках наблюдения М _Ѕ ( r ) на рисунке 3. В целом интерпретация результатов моделирования статистиче-

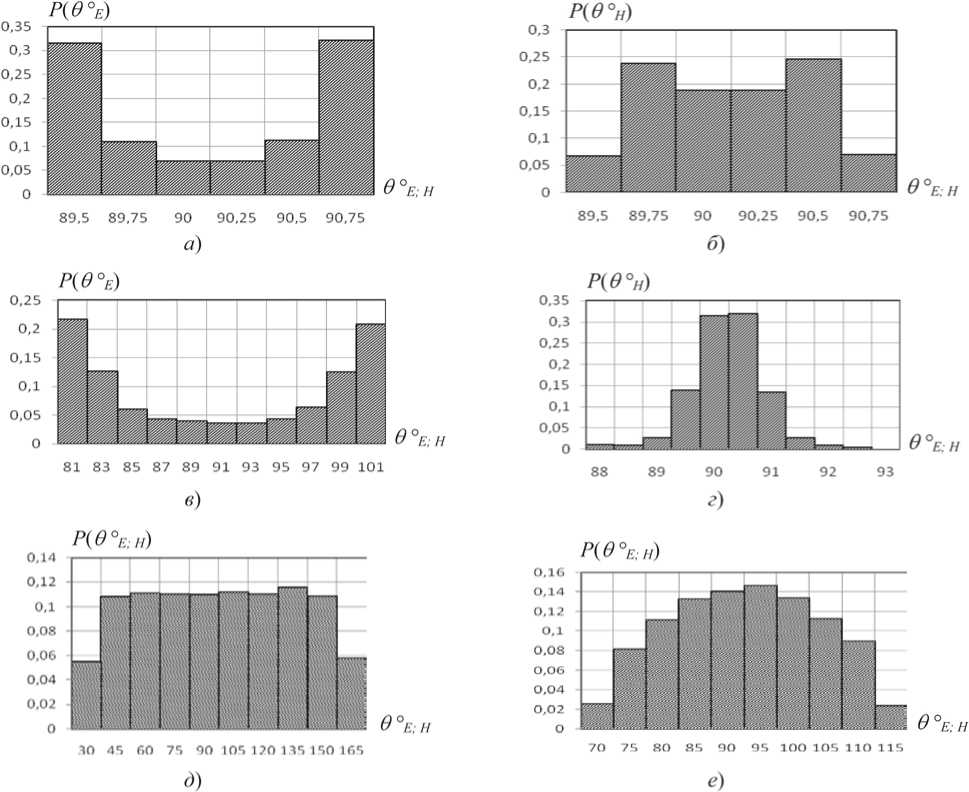
Рисунок 6. Гистограммы меридиональных углов О E . H для Е -поля и Н -поля АСА в осевой точке М _Ѕ (0; 0; 30) при комбинаторике и фазовых ошибках: а , б ‒ на частоте 10 кГц; в, г ‒ 150 кГц; д, е ‒ 1 МГц

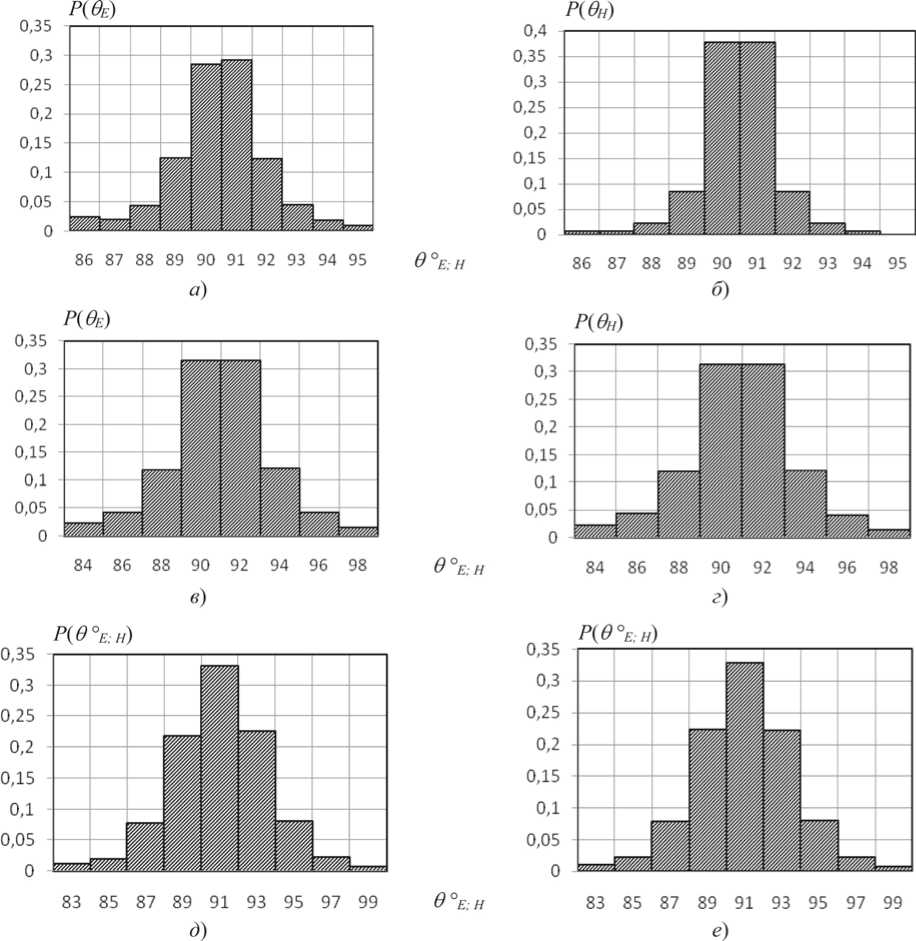
Рисунок 7. Гистограммы меридиональных углов 9 _Е . H для Е -поля и Н -поля АСА в осевой точке

М _Ѕ (0; 0; 30) при комбинаторике и фазовых ошибках։ а , б ‒ на частоте 150 МГц; в, г ‒ 500 МГц; д, е ‒ 10 ГГц

Таблица 2. Статистические характеристики азимутальных углов ф _Е . H для боковой точки M _s (30; 30; 30) при несбалансированных токах, вероятностной комбинаторике и фазовых ошибках

Частота, МГц	Вероятностная комбинаторика		Комбинаторика и фазовые ошибки
	P ( Ф E;H °)	5 ( Ф° Е ), %	P ( Ф E ; H °)	5 ( Ф° Е ), %
0,01	0,046 ± 0,025	± 54,3	0,047 ± 0,025	± 53,2
0,15	0,046 ± 0,026	± 56,5	0,046 ± 0,025	± 54,3
1	0,089 ± 0,081	± 91,0	0,042 ± 0,007	± 16,7
150	0,048 ± 0,024	± 50,0	0,043 ± 0,011	± 25,6
500	0,047 ± 0,025	± 53,2	0,041 ± 0,005	± 12,2
1000	0,048 ± 0,024	± 50,0	0,043 ± 0,006	± 13,95
10000	0,047 ± 0,024	± 51,1	0,043 ± 0,004	± 9,3

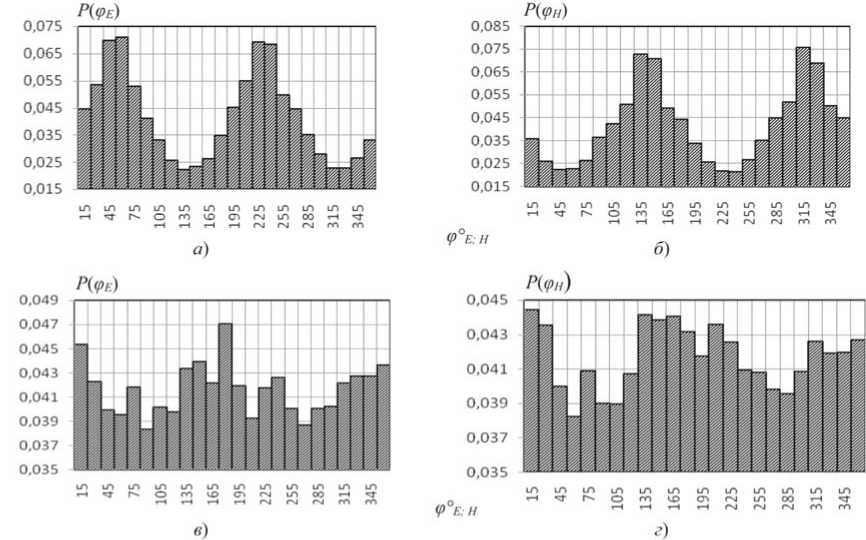
Рисунок 8. Гистограммы азимутальных углов ϕ _{E ; H} для Е -поля и Н -поля АСА в боковой точке М _Ѕ (30; 30; 30) при комбинаторике и фазовых ошибках: а; в ‒ на частоте 10 кГц; б; г ‒ 10 ГГц

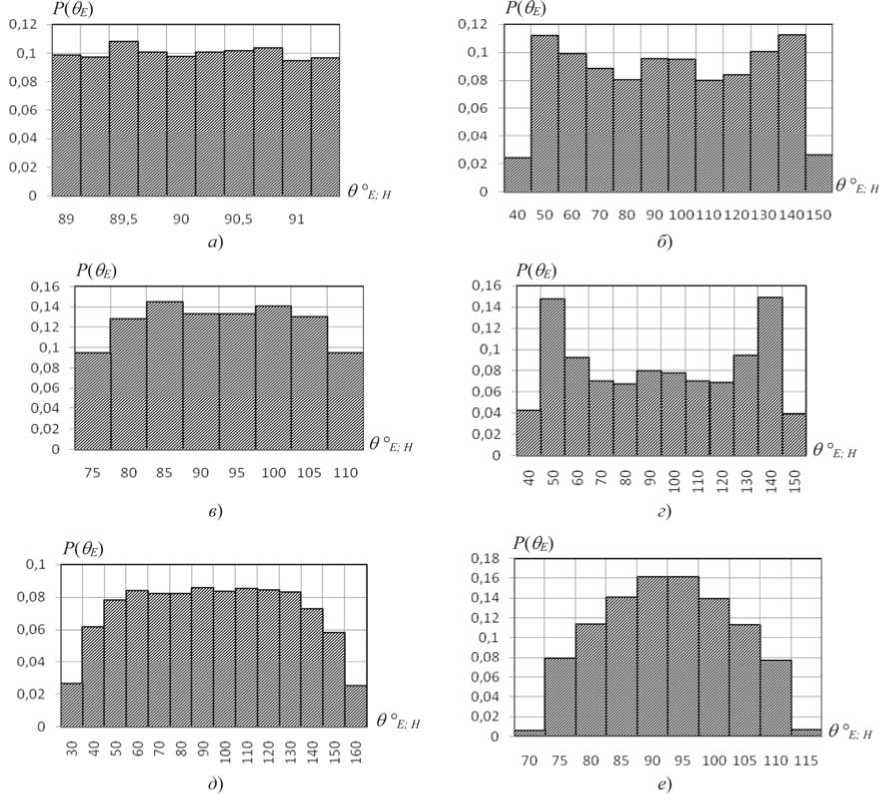
Рисунок 9. Гистограммы меридиональных углов θE;H для Е-поля и Н-поля АСА в боковой точке МЅ (30; 30; 30) при комбинаторике и фазовых ошибках: а, б ‒ на частоте 10 кГц; в, г ‒ 150 кГц; д, е ‒ 1 МГц ских характеристик углов фE.H и ОE.H для Е-поля и Н-поля АСА позволяет сделать следующие выводы.

• 1.    Главным фактором, определяющим результаты моделирования во всех рассмотренных случаях, является вероятностная комбинаторика, которая автоматически учитывает амплитудные ошибки возбуждения компонентов ТЭИ, формирующих ТКМ-модель АСА. По сравнению с моделью АСА на основе элемента Гюйгенса [17‐28], ТКМ-модель, благодаря вероятностной комбинаторике, обладает существенно большими возможностями для исследования стохастической поляризации.

• 2.    Расположение точки наблюдения М _Ѕ (осe‐ воe, боковое); баланс токов, возбуждающих компоненты ТЭИ; нaличие фазовых ошибок; xa-paктер кластеризации и изменение частоты в гармоническом режиме работы АСА являются фак-

• торами, существенно влияющими на результаты моделирования.

• 3.    Распределения азимутальных углов ф E . H на частотах от 10 кГц до 10 ГГц за сравнительно редким исключением - см. значения 5(ф E . H ) % в таблицах 1‐2, близки к равномерному закону։ это говорит о том, что все направления проекций векторов Е -поля и Н -поля на поперечную плоскость ХОҮ фактически равновероятны.

• 4.    Статистические свойства меридиональных углов О E . H на частотах до 1 МГц и на частотах выше 1 ГГц различаются между собой как по характеру гистограмм, так и по оценкам их числовых параметров ‒ при этом все они концентрируются вблизи О E . H = 90°, что также соответствует плоскости ХОҮ.

• 5.    С увеличением частоты унимодальные распределения углов ф E . H и О E . H нормализуются, что, по-видимому, говорит о выполнeнии усло-

  

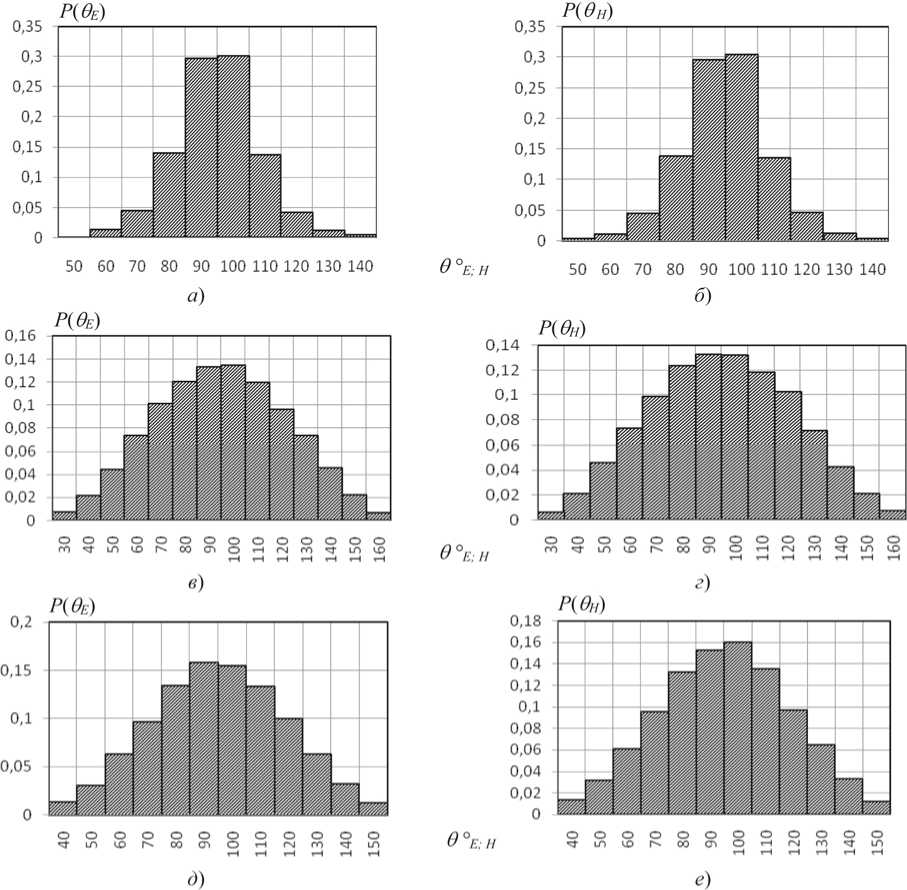
  Рисунок 10. Гистограммы меридиональных углов О E . H для Е -поля и Н -поля АСА в боковой точке

  M _S (30; 30; 30) при комбинаторикe и фазовых ошибках։ а , б ‒ на частотe 150 МГц; в, г ‒ 500 МГц; д, е ‒ 10 ГГц

  
  

• 6.    Наличие возрастающих по величине фазовых ошибок, а также увеличение с ростом частоты числа корреляционных кластеров во всех случаях увеличивают динамический диапазон значений ϕ _{E ; H} ᴎ θ _{E ; H} , а также деформируют (сглаживают и расширяют по экстремумам) их гистограммы.

вий применимости центральной предельной теоремы теории вероятности в данных ситуациях.

Таким образом, методы, средства и результаты анализа угловых характеристик векторов напряженности Е -поля и Н -поля, создаваемых объектом ТСА, демонстрируют как их практическую эффективность, так и специфические свойства стохастической поляризации радиоволн, которая здесь имеет место.

Актуальным представляется использование полученных данных при моделировании каналов утечки конфиденциальной информации, а также в других прикладных задачах ТСА.