Полная потенциальная энергия конструкции с односторонними связями и ее использование при решении задачи устойчивости

При классическом анализе устойчивости линей-но-деформируемых конструкций, имеющих сжатые элементы, внешнее силовое воздействие делится на две части. Прежде всего, это воздействие P , зависящее от параметра λ , которое вызывает большие осевые усилия и приводит к потере устойчивости при критическом значении величины λ . Такую нагрузку принято называть параметрической [8]. В отличие от нее, активная нагрузка Q вызывает только изгиб (кручение) элементов конструкции, тогда как осевые деформации или отсутствуют вообще, или пренебрежимо малы. Эти термины, введенные при обращении к задачам устойчивости систем с двухсторонними связями, утрачивают свою определенность, как только речь заходит о конструкциях с односторонними связями. Дело в том, что воздействие Q оказывает существенное влияние как на величину критической силы, так и на форму потери устойчивости таких конструкций, поэтому приходится следить за перемещениями и усилиями системы по мере изме- нения нагрузки Q , характеризуемого неким параметром μ . Сказанное означает, что нагрузка Q становится столь же параметрической, сколь и нагрузка P . С другой стороны, при наличии воздействия Q нагрузка P ведет себя не менее активно, чем нагрузка Q , вызывая деформации изгиба еще до достижения своего критического значения и способствуя переходу от одной рабочей системы к другой. Поэтому при решении задач устойчивости систем с односторонними связями лучше отказаться от использования терминов параметрическая нагрузка и активная нагрузка и перейти к представлению внешнего воздействия в виде двух составляющих по признаку их вхождения в выражение для полной потенциальной энергии Π конструкции. Ту его часть, которая определяет квадратичные слагаемые в выражении для энергии Π (но может частично определять и линейные члены), естественно называть λ -компонентой или λ -составляющей заданной нагрузки, а долю воздействия, входящую только в линейную часть энергетиче-

ской квадратичной формы, – ее μ -компонентой ( μ -составляющей).

Задача состоит в отыскании критической нагрузки на конструкцию, то есть в определении критического значения параметра λ в предположении, что перемещения малы. При консервативной нагрузке эта задача может быть решена энергетическим способом, поэтому интересно выяснить, как меняется полная потенциальная энергия Π системы по мере изменения параметров λ и μ . Эта энергия представляет собой неоднородную квадратичную форму обобщенных перемещений, что позволяет анализировать зависимость Π ( λ , μ ), опираясь на теорию квадратичных форм. В настоящей работе рассматривается система с конечным числом n степеней свободы. Ее состояние характеризуется кинематическими параметрами q 1 , q 2 , „., q n . Числа q n образуют вектор-столбец q . Поскольку квадратичная форма определяется в линейном пространстве без обращения к метрике этого пространства, все положения, устанавливаемые для квадратичных форм в конечномерных пространствах, справедливы и в пространствах бесконечной размерности. О тех свойствах квадратичных форм, которые потребуются в дальнейшем, кратко напоминается в п. 1. При этом используется запись потенциала Π ( λ , μ ) для конструкции с двухсторонними связями.

АНАЛИЗ ПОЛНОЙ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ УПРУГОЙ СИСТЕМЫ

Полная потенциальная энергия рассматриваемой системы

Π=Φ 0 -Φ 1 q + ¹ ₂ q ^т Φ 2 q         (1.1)

является неоднородной квадратичной формой обобщенных перемещений q_i , которые представлены в формуле (1.1) вектором-столбцом q из n элементов. Через Φ ₀ обозначена потенциальная энергия предварительного напряжения. Линейная часть формы (1.1) задается вектором-столбцом Φ 1 =Φ 1 ( λ , μ ), а ее квадратичная часть – матрицей Φ ₂ =Φ ₂( λ ). Решение задачи устойчивости сводится к минимизации квадратичной формы (1.1) по вектору q в открытой области.

В зависимости от значений параметров λ и μ квадратичная форма (1.1) может быть определенной по знаку или знакопеременной. В первом случае квадратичная форма относится к эллиптическому типу, во втором – к гиперболическому либо параболическому типу. Характер стационарных точек у форм разных типов различен, поэтому приходится следить за тем, как изменение параметров λ и μ влияет на изменение типа квадратичной формы (1.1). Наиболее наглядна каноническая форма представления функционала Π ( λ , μ ). Такое представление достигается преобразованием координат q_i .

Параллельный перенос начала координат q=q+q0(1.2)

позволяет избавиться в равенстве (1.1) от слагаемых первого порядка:

Π=Φ0+12qтΦ2q.(1.3)

Здесь

Φ0=Φ0-12Φ1Φ-21Φт1.(1.4)

Вектор q 0 сдвига начала координат определяется равенством q0=Φ2-1Φ1т.(1.5)

Вычисления по формулам (1.3)–(1.5) возможны лишь при невырожденной матрице Φ2 , то есть при условии, что ее определитель nn detΦ2 =γ∑(ϕi-λ)≡γ∑νi        (1.6)

i = 1                             i = 1

отличен от нуля. Через ϕ _i обозначены собственные числа матрицы Φ 2 , а через γ – некоторая константа. Кроме того, введено обозначение ν i = ϕ i -λ . О выполненном преобразовании говорят как о приведении квадратичной формы к центру. Квадратичная форма (1.1) не имеет центра тогда и только тогда, когда параметр λ совпадает с каким-либо из собственных чисел матрицы Φ ₂ старших членов. Последующий поворот осей базиса q _i :

q = Lq (1.7)

приводит квадратичную форму к сумме квадратов.

Символом L обозначается ортогональная квадратная матрица порядка n . Ее столбцами являются собственные векторы e _i матрицы Φ ₂ :

^L = ^[e 1 e 2 - e n ]-                 (1-8)

Так как Lт =L-1 , LLт=LтL=E, то qт Ф 2 q = qт LT L Ф 2 LT Lq = т V = V т = j^ Vq 2, i =1

где ν – диагональная матрица с ненулевыми элементами νi , и n п = ф о + т j v,q 2.            (1.9)

2 i = 1

Из формул (1.2) и (1.7) следует, что q = L q + q0.                (1.10)

Связь между исходной и конечной системами координат определена.

Если 0 < ф 1 < ф ₂ <  . .< ф n и X < ф 1 , то все v i положительны. Квадратичная форма (1.9) является эллиптической и положительно определенной. У нее единственный минимум, достигаемый при q = 0. Согласно формуле (1.10), в этом случае q = q ₀, то есть точкой минимума является центр квадратичной формы (1.1). Его положение зависит от параметров нагружения X и ц . Однако положение такого центра не влияет на характер стационарной точки. Состояние системы устойчиво.

Если X > ф n , то все v i <  0, и эллиптическая квадратичная форма (1.9) определена отрицательно. Теперь при q = 0 ( q = q ₀) энергия П максимальна, тогда как ее минимум неограничен. Отвечающее стационарной точке равновесное состояние системы неустойчиво. Возрастая, параметр X раньше или позже достигнет значения Ф 1 , став равным первому характеристическому числу матрицы Ф 2 , что отвечает потере устойчивости системы. Определитель этой матрицы обращается в нуль (см. формулу (1.6)), поэтому центр у соответствующей квадратичной формы отсутствует. Преобразование энергии (1.1) приходится сразу начинать с поворота репера q (строение (1.8) у матрицы L сохраняется):

q = L q .                  (1.11)

Подстановка вектора (1.11) в выражение (1.1) дает:

n

П = Ф 0 -Ф 1 L т q + - Е v q 2 .       (1.12)

² i = 1

Пусть    Ф1 L = [T1 Т2 .тn ]    и q 1 = q1, qi = qi-тi/vi, i = 2,3,...,n. Тогда

1 ⁿ

^П = ^Ф 0 -T 1 q 1 +- Е v i q i        (1.13)

² i = 2

при

1 _T 2

Ф0 = Ф0+ Д

2 i=2 v i и всех строго положительных числах vi. Запись (1.13) является канонической для потенциальной энергии системы, если v1 = 0 .

Квадратичная форма (1.13) относится к параболическому типу. При любых конечных значениях координат q2, q3, . , qn и | qx\ ^ ^ энергия (1.13) неограниченно убывает или возраста- ет в зависимости от соотношения знаков величин т1 и q 1. Стремление величины \ q1\ к бесконечности свидетельствует о потере устойчивости системы. Если положить в формуле (1.3) Фо = Ф1 = 0, то преобразование (1.11) при Ф1 - X = v1 = 0 сразу же приводит эту форму к виду:

^П = 2^{( v} 2 q 2 ^+v 3 q з ⁺ . ^+v пСп\

Ее минимум достигается при произвольном значении координаты 1 и нулевых значениях всех остальных координат q вектора

= e 1 .

Значит, возможно равновесное состояние системы и при ненулевых перемещениях, характеризуемых вектором q , ортом которого является первый собственный вектор матрицы Ф ₂ . Подстановка вектора q в формулу (1.12) дает:

П = Ф ₀ -Ф 1 е 1 .             (1.12 а )

Подобная картина наблюдается и тогда, когда параметр X принимает значения ф ₂, . , ф _n . Но при ф i < X < ф i _{+ 1} рассматриваемая квадратичная форма становится гиперболической. Преобразования (1.2) и (1.7) приводят ее к виду:

^П = ^Ф 0 ⁺ :2 ^{( -v} 1 1²----- ^v i q 2 ^{+ v} i + 1 "+1 ^{+ — + v} n 2 ).

Теперь функция П () имеет единственную стационарную точку – седловую. Ей отвечает исходное состояние равновесия системы. Более подробные сведения о приведении квадратичных форм к каноническому виду можно найти в монографии [9].

СИСТЕМЫ С ОДНОСТОРОННИМИ СВЯЗЯМИ

Модель конструкции с односторонними связями можно назначить так, чтобы все они были интерпретированы как абсолютно жесткие. Именно такая модель здесь и рассматривается. Первый вопрос, возникающий при ее изучении, это вопрос о числе степеней свободы системы. Определение данного числа – операция довольно громоздкая и при отсутствии односторонних связей, ибо жесткие тела могут сопрягаться друг с другом и с землей произвольно ориентированными абсолютно жесткими, абсолютно податливыми и упруго податливыми связями. Одно только описание этих связей требует определенной аккуратности и по- следовательности [6]. Но здесь вычислительные операции обычны: число C* степеней свободы конструкции, у которой нет односторонних связей, может быть найдено по формуле:

C * = 6 D - r , (2.1)

где D – число тел, а r – ранг матрицы кинематических уравнений конструкции, состоящей из абсолютно жестких тел при разнообразных связях между ними. Громоздкость вычислений по формуле (2.1) связана с формированием матрицы кинематических уравнений.

Степень свободы n конструкции, имеющей m односторонних связей, приходится находить как разность n = C * - C * (2.2)

где C ^* – число степеней свободы подконструкции K ₀ , получаемой из заданной конструкции при удалении всех односторонних _*связей. Это число дается формулой (2.1). Через C ^* обозначено число степеней свободы, которое утрачивает подконструкция K ₀ после возвращения ей ранее устраненных односторонних связей. Пусть u _j – параметры стояния подконструкции K ₀ . Односторонние связи накладывают на эти параметры ограничения

C ^*

£ a j u j >  0, i = 1,2, ... , n .

j = 1

(2.3)

Неоднородные ограничения на перемещения u _j пока не рассматриваются. Такие ограничения бывают тогда, когда связи поставлены с зазорами. Однако зазоры конечной величины при сколь угодно малых перемещениях системы не перекрываются, а потому они не учитываются.

Среди ограничений (2.3) могут встретиться противоречивые неравенства. Их необходимо исключить, опираясь, например, на положения, сформулированные в п. 4 главы I монографии [10]. Пусть несовм е стимые неравенства содержат в совокупности m различных параметров u_j . Если эти параметры положить равными нулю, что равносильно погашению m степеней свободы в подконструкции K ₀ , то п ротиворечия б удут сняты. Следовательно, C * = m и n = C * - m . (2.2 а ) Так как перемещения по направлению указанных m связей невозможны, допустим переход от заданной конструкции к системе, у которой противоречивых ограничений на перемещения уже не будет.

Среди условий, оставшихся в системе (2.3) после удаления несовместных неравенств, могут быть зависимые соотношения. Таковые также должны быть устранены. Это делается при помощи алгоритма, предложенного в п. 3 главы III уже упоминавшейся работы [10]. В результате реальных ограничений в системе (2.3) не будет больше числа (2.2а).

На рис. 1а изображена схема конструкции с шестью односторонними связями, воспринимающими только сжатие. Ее подконструкция K ₀ имеет 4 степени свободы (рис. 1b). Такой же результат может быть получен и по формулам (2.1)–(2.2). Горизонтальными перемещениями дисков (абсолютно жестких стержней) можно пренебречь, поэтому названные формулы сводятся к соотношениям:

C * = 2 D - r = 8 - r , n = 8 - r - C * .     (2.4)

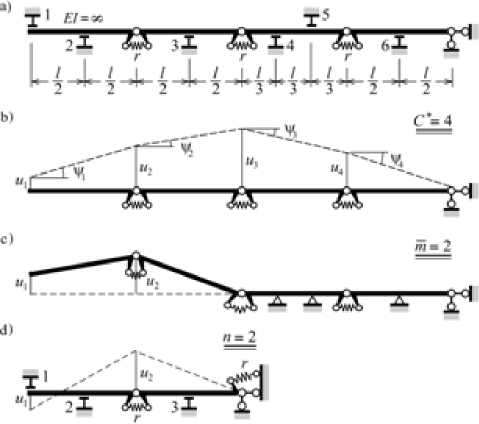
Рис. 1. Определение числа степеней свободы

Кинематические уравнения подконструкции K ₀ связывают между собой линейные u_j и поворотные v i перемещения дисков:

U1 - u2 + V11 = 0, u3 - u4 + V31 = 0, u2 - u3 + V21 = 0, u4 + V41 = 0.

Ранг этой системы равен четырем: r = 4, поэтому

C * = 4, n = 4 - C * .           (2.4 а )

Остается учесть влияние односторонних связей. По рис. 1 видно, что односторонние связи 1–6 накладывают на перемещения u_i следующие ограничения:

• 1.    - u 1 >  0;

• 2.    u 1 + u ₂ >  0;

• 3.    u ₂ + u 3 >  0;

• 4.    2 u ₃ + u ₄ >  0;

• 5.    - u 3 - 2 u 4 >  0;

• 6.    u ₄ >  0.

Так как и 4 >  0 , ограничение 5 может выполниться лишь при условиях, что и 3 <  0 и | и 3 | > 2 и 4 . Но тогда (см. условие 4) 4 и 3 + 2 и ₄ = = 3 и 3 + ( и 3 + 2 и ₄) <  0, ибо слагаемые 3 и 3 и ( и ₃ + 2 и ₄) отрицательны. Следовательно, неравенства 4–6 противоречивы. Входящие в них пере м е_*щения приравниваются к нулю. Тогда m = C * = 2, и, согласно формуле (2.4 а ), n = 2. Полученной конструкции (рис. 1с) надо вернуть связи 1–3, одновременно с этим превратив остальные односторонние связи в двухсторонние. Результатом таких действий является система, изображенная на рис. 1d.

После решения вопроса о степенях свободы конструкции можно составить выражение (1.1) для ее полной потенциальной энергии. Ясно, что это будет энергия подконструкции K0 . Множество ортонормированных собственных векторов данной подконструкции является базисом пространства решений задачи об устойчивости рассматриваемой конструкции с односторонними связями. Такие решения должны удовлетворять ограничениям aq + в> 0,                 (2.5)

накладываемым на вектор q односторонними связями. В скалярной записи эти ограничения таковы (величины a j и в i известны):

£ a _y q_v +p i >  0, i = 1,2,   , n <  n .     (2.5 а )

j = 1

Если в i * 0, то связь с номером i поставлена с зазором.

Неравенство n <  n имеет место лишь тогда, когда система (2.5) не содержит противоречивых и линейно зависимых неравенств (см. выше комментарии к формулам (2.2 а ) и (2.3)). Это следует из результатов работы [11], в которой было показано, что лишить подвижности конструкцию с n степенями свободы можно не только при помощи правильно поставленных n двухсторонних связей, но и с помощью правильно поставленных односторонних связей числом n + 1. В последнем случае правильность расстановки связей как раз и заключается в отсутствии у системы (2.5) зависимых и несовместных неравенств. С тало быть, если связи поставлены правильно и n = n + 1, то конструкция неподвижна и вопрос о ее устойчивости отпадает сам собой.

При X < ф 1 квадратичная форма имеет центр и ее преобразование к каноническому виду осуществляется при помощи подстановки (1.10):

L т ■ q + q 0 .

Эта же подстановка используется при записи ограничений (2.5):

& q + в> 0,                 (2.6)

соблюдается, то и здесь система находится в состоянии устойчивого равновесия при q = q ₀. При нарушении неравенства (2.6 а ) решению задачи отвечает точка, находящаяся на границе допустимой области (2.5). Эта точка может либо принадлежать одной из прямых

n

£ a_A + b i = 0, (2.5 b ) j = 1

либо находиться на пересечении двух и большего числа прямых такого типа. Обращение неравенств (2.5 а ) в равенства (2.5 b ) означает, что одна или несколько односторонних связей оказались включенными, то есть равновесное состояние реализуется уже не в подконструкции K ₀ , для которой записывалась энергия (1.3), а в некоторой другой системе. Как бы то ни было, при X < ф 1 решение задачи доводится до конца обычными средствами математического программирования [2], [4].

Сложнее обстоит дело, когда X = ф i , i = 1,2,..., n . В этом случае (см. формулу (1.12 а )) стационарная точка определяется собственным вектором e i матрицы Ф 2 . Однако равновесное состояние системы, диктуемое этим вектором, возможно лишь при условии, что орт e _i принадлежит допускаемой области (2.5). Сказанное означает, что в зависимости от ограничений (2.5) реализоваться могут как все собственные векторы подконструкции K ₀ , так и ни один из них.

Выход вектора q на границу допустимой области означает переход от конструкции, у которой односторонние связи находились в нерабочем состоянии, к конструкции, обладающей одной или большим числом работоспособных односторонних связей. Полная потенциальная энергия новой конструкции по-прежнему описывается равенством (1.1), но только при других векторах q ‘ , Ф‘ и матрице Ф 2 . У подконструкции K ₀ ‘ новой кон с трукции в нерабочем состоянии находятся n ‘ <  n связей, но опять же реализоваться могут как все собственные векторы матрицы Ф 2 , так и ни один из них.

Пусть M – множество всех подконструкций, которые получаются из заданной конструкции при удалении различных сочетаний односторонних связей и в которых могут поддерживаться равновесные состояния при различных значениях параметра X . Пусть, далее, n * - общее число таких состояний. Несмотря на то что степень свободы заданной конструкции равна числу n , величина n * с этим числом, как правило, не совпадает. Возможны случаи n * <  n и n * >  n , причем весьма часто имеет место именно неравенство n * >  n .

С другой стороны, размерность пространства состояний конструкции равна числу ее степеней свободы, то есть числу n . Значит, при n * >  n из n * векторов q , описывающих состояния равновесия системы, n * - n векторов являются линейно зависимыми. Найти их, обращаясь только к полной потенциальной энергии Π подконструкции K ₀ , нельзя.

Нетрудно заметить, что при анализе квадратичных форм параметр μ фактически оставался фиксированным. Объяснить это можно тем, что старшие члены квадратичной формы не зависят от названного параметра, а потому изменение величины μ не сказывается ни на собственных числах, ни на собственных векторах матрицы Φ ₂ . Однако на положение центра квадратичной формы параметр μ влияет, и от него зависит, достигается ли минимум функции Π ( q ) внутри допустимой области или на ее границе, а если на границе, то на какой именно.

Критическая сила каждой рабочей системы может быть найдена в результате минимизации полной потенциальной энергии данной рабочей системы, причем получаемый минимум единственен. У каждой рабочей системы этот минимум свой, так что задача сводится к отысканию глобального минимума. В общем случае это можно сделать только перебором всех локальных минимумов, чем и объясняется громоздкость расчета на устойчивость систем с односторонними связями. Естественен вопрос о числе односторонних связей, при котором объем вычислений становится чрезмерным. Ответ на этот вопрос сегодня существенно отличается от ответа, данного, скажем, 10 лет назад, и наверняка сегодняшний ответ столь же существенно будет отличаться от ответа, который прозвучит через 10 лет. Потому заниматься следует поиском алгоритмов разумного перебора рабочих систем, созданием алгоритмов решения частных, но важных в практическом отношении задач и не рассчитывать на то, что удастся, как и при прямом статическом расчете конструкций с односторонними связями, обойтись методами, предназначенными для решения одноэкстремальных задач.

Осталось привести несколько примеров, иллюстрирующих высказанные выше положения. На рис. 2а изображена система, которая не имеет односторонних связей. Но такая система может выполнять роль подконструкции K ₀ конструкции с односторонними связями, для чего она и предназначается. Степень свободы этой системы равна 2, параметрами ее состояния выбраны углы поворота ψ 1 и ψ 2 крайних дисков. Через эти параметры выражается полная потенциальная энергия конструкции:

Π= 2 r { ψ ₁ ² + (2 ψ ₁ -ψ ₂)² + ( ψ ₁ - 2 ψ ₂)² + +ψ ² ₂ -λ [ ψ ₁ ² + ( ψ ₁ -ψ ₂)² +ψ ²₂]}.

(2.7)

Необходимые условия стационарности функции Π ( ψ 1 , ψ 2 ) таковы:

(6 - 2 λ ) ψ ₁ - (4 -λ ) ψ ₂ = 0,         (28)

(4 -λ ) ψ ₁ - (6 - 2 λ ) ψ ₂ = 0.            .

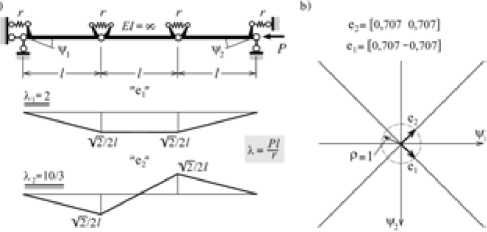
Рис. 2. Подконструкция К0 для ряда систем с односторонними связями

Значит, могут существовать два нетривиальных равновесных состояния, характеризуемых векторами с ортами e₁ и e₂ . Это собственные векторы квадратичной формы (2.7). На плоско сти 0 ψ 1 ψ 2 им отвечают лучи, вдоль которых направлены названные выше орты (рис. 2b).

Рассмотренная конструкция является подконструкцией K ₀ для системы, приведенной на рис. 3а. На нее наложено ограничение ψ 1 ≤ 0 , что сводит пространство перемещений к полуплоскости, которая на рис. 3b затемнена. Векторы e₁ и e₂ нетривиальных равновесных состояний сохраняются, лишившись, правда, своих «двойников» с противоположными знаками, и появляется еще один допустимый вектор с ортом e 3 ′ = [01]. Координаты ψ 1 = 0 и ψ 2 = 1 этого вектора при λ ₃ ^' = 3 системе (2.8) не удовлетворяют, хотя и обращают потенциальную энергию (2.7) в нуль, как и координаты ортов e₁ и e₂ при λ ₁ = 2 и λ ₂ = 3,333 соответственно. Видно, что вектор e₃ ′ является линейной комбинацией векторов e₁ и e₂ :

e 3 ′ =

- ² (e

-

e2).

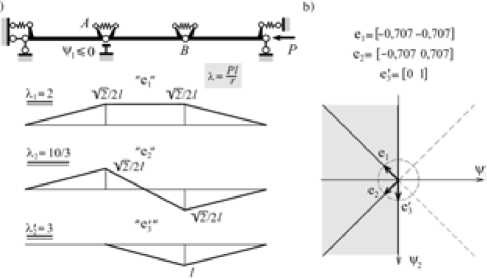
Рис. 3. Конструкция с одной односторонней связью

Добавление к шарниру B приведенной на рис. 3а конструкции односторонней связи, препятствующей перемещению этого шарнира вверх, приводит к ограничениям ψ 1 ≤ 0 и ψ 2 ≥ 0 на перемещения конструкции. Равновесное состояние, отвечающее вектору e₁ , станет невозможным. Останутся состояния, характеризуемые векторами e₂ и e₃ ′ , к которым добавится состояние с вектором

2 e ′ ₄ = ₂ (e₁ + e₂).

В этом случае именно параметры λ ₃ ′=λ ₄ ′= 3 являются критическими. Ни они, ни отвечающие им векторы e₃ ′ и e ′ ₄ к собственным числами и собственным векторам квадратичной формы (2.7) не относятся, но векторы e₃ ′ и e₄ ′ являются линейными комбинациями векторов e₁ и e₂ .

У конструкции, изображенной на рис. 4а, две односторонние связи, из которых одна включает упруго податливый элемент жесткостью r / l ² . Такая конструкция имеет четыре нетривиальные равновесные формы. Три из них не отвечают собственным векторам e₁ и e₂ базовой подконструкции K ₀ (см. рис. 3). Все они суть линейные комбинации последних:

e′2=0,1529e1+0,9882e2, e3′ =22 (e1-e2), e2).

е,- (OlWI 0.7071] el-I-O.59O? o^ow]

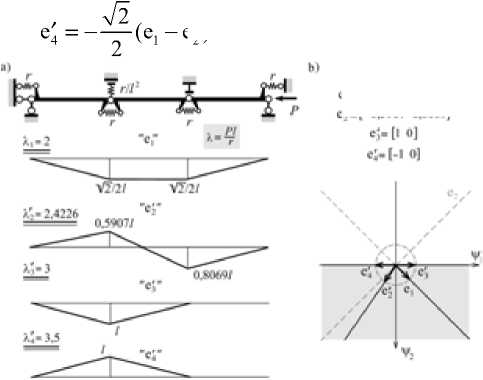
Рис. 4. Конструкция с упруго податливой и абсолютно жесткой односторонними связями

Здесь любопытно то, что двум различным собственным значениям λ ₃ ′ = 3 и λ ₃ ′ = 3,5 отвечают по существу одинаковые собственные векторы e₃ ′ и e ′ ₄ . Это зеркально случаю кратности характеристических чисел, когда одинаковым (кратным) собственным значениям отвечают разные собственные векторы.

И в заключение приведем пример конструкции, нетривиальные равновесные состояния которой характеризуют векторы e3′ и e4′ , не совпада- ющие ни с одним из собственных векторов e1 и e2 подконструкции K0 (рис. 5а). Это объясняется тем, что ограничения ψ1 ≥ 0 и -(ψ1 + ψ2)≥ 0 сузили допустимую область до конуса, в который ни вектор e1 , ни вектор e2 не попадают (рис. 5b).

Линейная зависимость ортов e _i ′ от единичных векторов e _i напоминает ситуацию, наблюдаемую при кратных характеристических числах симметрических матриц. Если кратность таких чисел равна p , то отвечающие им p собственных векторов линейно зависимы, что не является поводом к исключению из дальнейших рассмотрений как линейно зависимых векторов, так и сопряженных с ними собственных значений. Размерность пространства состояний в любом случае совпадает с числом различных собственных векторов, а не с числом различных собственных значений.

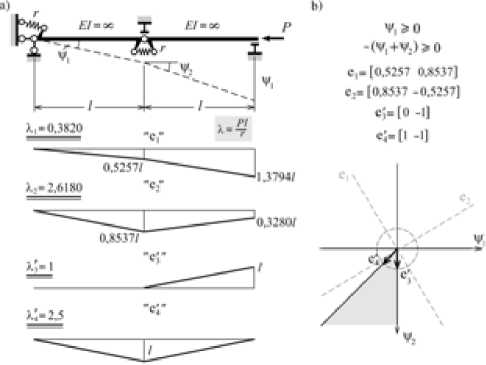
Рис. 5. Конструкция с двумя односторонними связями

Сказанное в предыдущем абзаце относится к конструкциям без односторонних связей. Однако нечто подобное можно сказать и о конструкции, у которой односторонние связи имеются. Только теперь под спектром эйлеровых сил следует понимать набор n * ≥ n сил, при которых возможны нетривиальные равновесные состояния системы, а собственные векторы – это все n * векторов, которые отвечают силам спектра. Недоразумений, связанных с использованием привычных терминов и понятий в непривычных ситуациях, можно избежать, если помнить о различиях между системами с двухсторонними и односторонними связями. Последние обладают рядом свойств, отсутствующих у систем с односторонними связями, а именно:

• 1.    Число нетривиальных равновесных состояний системы без односторонних связей совпадает с числом ее степеней свободы. Эта размерность может быть указана еще до решения задачи устойчивости.

• 2.    Для определения критической силы все остальные эйлеровы силы системы знать необязательно.

В задачах устойчивости конструкций с односторонними связями дело обстоит иначе:

• 1.    Число нетривиальных равновесных состояний системы с односторонними связями не совпадает с числом степеней ее свободы. Установить степень свободы такой системы можно лишь после анализа ограничений на ее параметры состояния, а число равновесных форм – только после того, как все такие формы будут обнаружены.

• 2.    Критическую силу можно указать лишь после того, как будут найдены критические силы всех рабочих систем.

Скажем несколько слов о приведении квадратичной формы к каноническому виду. При решении конкретных задач устойчивости необходимость в таком приведении отсутствует. Но если оно желательно, то выполнить вычисли- тельные операции с использованием матрицы (1.8) не удастся, так как столбцами этой матрицы являются компоненты собственных векторов квадратичной формы, а они до решения полной задачи устойчивости неизвестны. Однако имеются способы приведения квадратичной формы к каноническому виду, которые не требуют знания собственных векторов и собственных чисел матрицы старших членов этой формы. В монографии [1] такие способы описаны детально.

БЛАГОДАРНОСТЬ

Автор выражает свою признательность А. В. Перельмутеру, с которым предмет настоящей статьи неоднократно обсуждался и который существенно повлиял на отбор публикуемого материала.