Полное решение задачи синтеза фазокодированных сигналов с равномерным энергетическим спектром

Для решения ряда задач в радиотехнических системах используются сложные сигналы [1-5]. Основное требование при этом состоит в том, чтобы уровень максимального бокового лепестка должен быть минимальным (в идеальном случае равным нулю). Поэтому разработка эффективных методов синтеза сложных сигналов с хорошими корреляционными свойствами является актуальной задачей. Причем сигналы с идеальной корреляционной функцией имеют равномерный энергетический спектр. Особое значение среди сложных сигналов имеют дискретные фазокодированные последовательности с пик-фактором равным единице. Дискретный фазокодированный сигнал Г = {уп}о^-1 можно определить на основании выражения:

/„ =exp(zp„), n = 0,...,7V-l, (1) где фаза сигнала принимает любое значение из диапазона ф_п e[0;2zr], N - количество кодовых элементов в сигнале, а модуль каждого кодового элемента равен 1, т.е. |/„| = 1.

Циклическую АКФ можно определить на основе выражения:

Лт ~ Тп+т (mod Ny^n , Г = 0,1,..., jV —1.

В работе [2] приводятся некоторые известные фазокодированные сигналы, циклическая АКФ которых имеет нулевой уровень боковых лепестков: сигналы Френка, сигна лы класса р и сигналы, ассоциированные с ЛЧМ сигналом. В работах [6-8] рассмотрены вопросы синтеза и обработки особого вида сигнала - композиционного контура из полного семейства элементарных контуров.

Однако на сегодня задача синтеза всех возможных фазокодированных сигналов с нулевым уровнем боковых лепестков для заданной размерности N не является решенной. Целью данной работы является решение этой задачи. Отметим, что полученные результаты ранее обсуждались в работах [9-11].

Для исключения “повернутых комбинаций” введем ограничение:

/0=1-              (3)

Таким образом, требуется найти углы ф ], ф 2,..., ф ^-\, такие чтобы выполнялось условие равенства нулю всех боковых отсчетов циклической АКФ:

7о =^> 71 = °> 72 =0,..., 7дч =°- (4)

Записывая выражение энергетического спектра для фазокодированного сигнала Г = {^”}ол-1 как n-\ С гл V

Z/п -ехр -Ь— т-л , _л=0 kN)

m = 0..N-\, и учитывая, что

|роМа|2=...=Ы2=^

получим систему уравнении

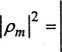
N-\ 2 И=1

(    2^)

cos ф_птп +

I    N)

м-\   (2л

+ 2 cos р„-р;+ —

/=„+1   <

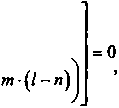
где М =

2k, для k (mod 2) = 0; к, для к (mod 2) = 1.

2л ~N\

- число взаимно-простое с

(5) на основании которой и будем искать углы

Ф1> Ф2’ •••> Ф N-\ •

Базисные решения

Анализируя систему уравнений (5) можно доказать, что для хотя бы одного решения должно выполняться условие:

№ = Фн-\. Фг=Фк-1» •-. (Р\н12\=Ф\к11\, ^

где ]•[ - означает целую часть числа. Такое решение назовем базисным.

Исходные базисные решения можно определить на основании выражений:

Ф1,п=Ф1\"² (mod N^Y (7)

2N, для N (mod 2) = 0, N, для N (mod 2)si.

, _ 2л п = 0,1,2,...,7V-1, fl - ^^> ^ -числовза имно-простое с числом Nx, I = 1,2,...,ф(7^);

Ф^1 ) " функция Эйлера.

Если размерность фазокодированного сигнала 7V является квадратом некоторого целого числа к , т.е. ^ ₌ £², то исходными базисными решениями системы уравнений (5) будут также являться решения вида:

Ф«л⁼Ф$^кх (8)

'_______________к_______________ 01;ll;...;(t-l)l;

______________к______________

*-3;(*+1)-3;...;(2*-1)-3;..;

(mod Л/)

(t2 -*](2t-l);..;(t2 -l)(2fc-lj числом Mi s = \,2,...,ф^му Ф^М^ - функция Эйлера от числа м •

Кроме того, если к является четным числом, то кроме решений вида (7) и (8) существуют исходные базисные решения системы уравнений (5) вида:

Ф$,п=Ф$'^кх           (9)

	*/2           t
	0;0;0;...;0;2 1;2-2;...;2*Л; к
X	4-(* + 1);4-(^ + 2);...;4-2^;....; *rl	(mod2jt)
	2(t-l)(t-l)2;..;2(t-l)(*z-t-l]; Ml Ь;0;...;6

, _ 2л .

где Vs ~      , Xs - число взаимно-простое с числом к, s = У,2,...,ф^ку

Группа Галуа системы уравнений (5)

Можно доказать, что корни системы уравнений (5) ф_х, ф_г, ..., ф _N_\ удовлетворяют операциям взаимной замены - подстановкам, не нарушающим соотношения между корнями системы уравнений. Если индексы корней системы уравнений (5) 1,2,3,...,7V-1 умножить на число X взаимно-простое с числом N , то получим, что каждый и-ый корень, где и = 1,2,3,...,7V-1, перейдет в новый корень с индексом Х п (mod TV).

Такую подстановку будем представлять в виде:

(о

тЛ= 4

О ^Л

I г (mod N^

У-l

Я/ (У-1) (mod ^) J ’ где / = l,2,...,p(7V1), ф(^ - функция Эйлера. Совокупность подстановок вида

Gal(T) = [тХ| ,Тх2 .....Тх^ |,     (П)

образует группу Галуа ф(^) -го порядка, где

/ = 1,2,...,ф(^).

Если размерность фазокодированного сигнала ^ -к², то решение системы уравнений (5) можно рассматривать в виде матрицы:

0	1	к-1
' Фо	Ф\	•• Фк-\
Фк	Фк+\	- Р21-1
Ф^к-Vyk	Ф(к-\}к+\	- ^-1

= [0 1 ... к-1], для которой допустимыми являются подстановки вида:

4 =

0 Г О

1         ...           к-1

Г          ...             1

Л/ • 1 (mod к) ... 2/ • (4 -1) (mod к^

(12) где Я, - число взаимно-простое с числом к, I = l,2,...,p(fc), ф(Л) - функция Эйлера. Данные подстановки меняют местами столбцы матрицы ф, в результате чего получаем новое решение системы уравнений (5) в матричном представлении вида Ф_Л=Я-[0 1 ... k-1] (modi).

Совокупность подстановок вида (12)

Gal(S)-|Sxl,SX2,...,Sxi||(i)^      (13)

образует группу Галуа ф(£)-го порядка дополнительных подстановок.

В случае четных значений числа к группу Галуа подстановок корней системы уравнений (5), образованную выражениями (11),(13), можно дополнить. Вспомогательный индекс 5 определим из выражения n=s-k/2 (mod ^). С учетом такого циклического сдвига из матрицы ф можно получить матрицу Y =

^’-«/г»!    "•     ^фк^г-\     Ф»

ФЦ1   ФкГьх ФкЦ»г    -

«>1/2-1

Л=-1/2-1 Фк1-мг-\ Ф^-мг к-2 к-1

для которой допустимыми являются подстановки вида:'

УЛ =

О

О

1         ...1-1

4          ...Г

Я;-1 (modi) ... ^(1-1) (modi)

(14) где X; - число взаимно-простое с числом к, I = 1,2,..., <р(Аг), ф(Л) - функцияЭйлера. Данные подстановки меняют местами строки матрицы «р, в результате чего получаем новое решение системы уравнений (5) в матричном представлении вида Yl=2 [0 1 ... k-l]^T (mod к\

Совокупность подстановок вида (14)

Gal(V) = {vX|,Vx2,...,Vxv(t)) (15)

образует группу Галуа ф(1)-го порядка дополнительных подстановок.

■ После применения подстановок вида (15) к решению системы уравнений (5), представленного в виде матрицы у, необходимо выполнить обратный переход от матрицы ч» к матрице ф, используя выражение п = s - k/2 (mod TV).

Небазисные решения системы уравнений (5)

Применяя допустимые подстановки корней системы уравнений (5) в виде (11,13,15) к исходным базисным решениям в виде (7-9), мы получим все возможные базисные решения. Общее количество базисных решений системы уравнений (5) размерности TV обозначим через £ • Для каждого полученного базисного решения можно получить еще N не базисных решений, используя преобразования вида:

Vn^lN.N-п*т (mod N^

= (mod 360°),   (16)

Общее количество возможных решений системы уравнений (15) обозначим через р. Выше было показано, что следует различать 3 случая:

• 1.    Для произвольного TV, где ^ * к¹, к - целое положительное число определим общее количество решений:

• 2.    Для /у ₌ £², где к - нечетное число количество возможных решений:

• 3.    Для рр -к¹, где к - четное число количество возможных решений:

  - в случае четных к[2

^’ = ф(^)^,         (17)

причем количество базисных решений для нечетного TV равно L = ф(TV), а количество базисных решений для четного TV равно £ = ф(2^.

Р = (ф(#)ф(Л) + 5^ф(*)1.М =

= ^W)M,    (18)

причем количество базисных решений в этом

Р =

ф(2ЛГ)ф(4)+^Зф(2*)ф(*)+^5ф(*)1х хн.»(Мй.^№УМ1 (19а) количество базисных решений в этом случае „,„^*«9(5,^)).

- в случае нечетных к/2:

Р=

ф(2Л0ф(*)+^рф(2*)ф(*)+^рф(*))х

_Ху = ^^^ (9 + 2_Ф(^)).^, (19,6) количество базисных решений в этом случае: ^ЗМ!.^^.

Особый случай TV = 4

Рассмотрим теперь особый случай, при котором длина кодовой последовательности TV = 4 • Система уравнений (5) с учетом существования базисного решения может быть представлена в виде:

{ 2созф] +cosy>2 + l + 2cos(p! -<Р1\

-cosy>2-l = 0.        ^

Откуда следует, что р₂ = 180°, а ^ и, следовательно, <Рз могут принимать любое значение из диапазона ^0°;360°j, т.е. Ф\ =<Рз е£о°;36О°]. Поэтому существует бесконечно много базисных решений вида 0°,^,180°,фр (21,а)

случае равно

i-^T<9.

где ф_х может принимать любое значение из

диапазона [о0; 360° j. С учетом преобразований (16) решениями системы уравнений (20) будут также являться решения вида:

О",^^0,^+180°.     (21,6)

Подчеркнем, что только в особом случае, т.е. при N = 4, можно синтезировать сколь угодно много кодовых последовательностей, имеющих нулевые боковые лепестки циклической АКФ, т.е. р = оо, причем количество базисных решений в этом случае равно £ = оо ■ Во всех остальных случаях, с учетом ограничения р₀ = 0°, количество кодовых последовательностей будет конечным.

Взаимно-корреляционные функции (ВКФ) полученных фазокодированных последовательностей

Среди множества р фазокодированных последовательностей размерности N в случае нечетных N можно выделить алфавит “квазиортогональных” сигналов, ВКФ которых будет равномерной и иметь уровень i/s/n • Таким образом, синтезированные сигналы можно использовать не только для решения задач разрешения и оценки параметров (основное требование к сигналам в этом случае - нулевой уровень циклической АКФ [8]), но и для решения задачи распознавания (основное требование в этом случае - выбор алфавита ортогональных сигналов [8]).

Выводы

В данной работе решены следующие задачи:

• 1.    Определено количество р всех возможных фазокодированных последовательностей заданной размерности N с нулевыми боковыми лепестками циклической АКФ и равномерным энергетическим спектром.

• 2.    Разработан обобщенный метод синтеза всех возможных р фазокодированных последовательностей для заданной размерности N . Показано, что все известные на сегодня фазокодированные сигналы могут быть син

• 3.    Синтезированы все возможные фазокодированные последовательности для заданной размерности N •

• 4.    Из полного множества фазокодированных последовательностей в случае нечетных размерностей N выделен алфавит сигналов, имеющих равномерную ВКФ с уровнем

  Работа выполнена при финансовой поддержке гранта РФФИ №04-01-00243

тезированы в соответствии с разработанным единым методом.