Полностью регулярные коды в треугольной решетке

Раскраска регулярного графа совершенна, если любые две вершины одного цвета имеют один и тот же цветовой состав окрестности. Если совершенная раскраска является раскраской по расстоянию от некоторого кода, то этот код - полностью регулярный, а такая раскраска - дистанционно регулярная. Полностью регулярные коды являются ключевым понятием и потому активно исследуются в дистанционно регулярных графах [8], в которых любая вершина является полностью регулярным кодом.

Из графов, не являющихся дистанционно регулярными, возможно, наибольший интерес в плане отыскания полностью регулярных кодов представляют бесконечные графы решеток. В работах [7, 3, 10] было получено описание всех совершенных раскрасок двумерной квадратной решетки в два, три и не более девяти цветов соответственно, в [1] изучены все ее дистанционно регулярные раскраски. В [6] установлено, что в n-мерной квадратной решетке радиус покрытия любого нередуцируемого (т.е. не являющегося объединением гиперплоскостей) полностью регулярного кода не превышает 2п. В [5] дано описание всех полностью регулярных кодов в гексагональной решетке (являющейся бесконечным 3-регулярным графом). В [4] показано, что для любой совершенной раскраски в гексагональной и треугольной решетках существует совершенная периодическая с теми же параметрами. В данной статье производится описание всех полностью регулярных кодов в треугольной решетке, которая является бесконечным 6-регулярным графом. Вершины треугольной решетки можно отождествлять с так называемыми целыми числами Эйзенштейна-Якоби. С ними связаны графы Эйзенштейна-Якоби, коды в которых

были впервые рассмотрены в [9], а в [2] были исследованы совершенные коды в них; такие кодві используются для передачи сообщений по каналам связи с комплекснозначной модуляцией.

Статья организована следующим образом. Далее в текущем разделе вводятся необходимые определения. В разделе 2 обсуждаются редуцируемые дистанционно регулярные раскраски и устанавливается (теорема 1), что любая нередуцируемая имеет не более трех цветов. В разделе 3 формулируется основной результат - теорема 2, которая затем доказывается в разделах 4 и 5 перебором всех возможных параметров дистанционно регулярных раскрасок в три и два цвета соответственно. Далее (раздел 6) следуют некоторые замечания и затем Приложение, содержащее список всех найденных кодов.

Перейдем к определениям. Разбиение (Р0, Pi,..., T^—i) множества вершин регулярного графа называется совершенной раскраской, если для всяких г, j Е {0,1,..., к— 1} существует такое число a-j, что любая вершина из Р смежна в точности с a-j вершинами из Vj. Матрицу А = (a-j ) назовем матрицей параметров этой раскраски. Из определения сразу следует, что сумма элементов любой строки матрицы параметров равна степени вершин графа.

Совершенную раскраску будем называть дистанционно регулярной, если ее матрица параметров трехдиагональна, т.е. каждая вершина может «видеть» только вершины своего цвета, а также предыдущего и последующего цветов. Это также означает, что в дистанционно регулярной раскраске каждая вершина имеет цвет, равный расстоянию до множества вершин нулевого цвета: р = { v : d(v, P0) = г}. Множество P0 называется полностью регулярным кодом. Очевидно, что одновременно и множество Vfe-i будет полностью регулярным кодом. В дальнейшем мы будем рассматривать только дистанционно регулярные раскраски в к цветов, к Е N, для которых выполнено условие, что для каждого цвета есть хотя бы одна вершина этого цвета. Как следствие, элементы aoi, ai2,..., a_n-i,_n и ащ, a2i,..., a_n,_n-i трехдиагональной матрицы параметров такой раскраски все отличны от нуля. Условимся следующим образом записывать матрицу параметров раскраски, если она дистанционно регулярна:

^А = ^[a00^a0i ^{— a}i0^aii^ai2 ^— . . . ^{— a}i,i-i^aii^ai,i+i ^— . . . ^{— a}k-i,k-2^ak-i,k-i\.

Матрицы параметров дистанционно регулярных раскрасок имеет смысл рассматривать с точностью до центральной симметрии. Действительно, раскраски с матрицей параметров

[afc-i,fc-iafc-i,fc-2 — . . . — ai,i+iawai,i-i — . . . — ai2aiiai0 — a0ia00]

получаются из раскрасок с матрицей параметров А взятием обратного порядка цветов.

Две дистанционно регулярные раскраски будем называть эквивалентными, если одна получается из другой автоморфизмом графа или обращением порядка цветов. В данной статье все раскраски рассматриваются с точностью до эквивалентности. Подчеркнем, что эквивалентность дистанционно регулярных раскрасок не означает эквивалентности полностью регулярных кодов, получаемых из раскрасок взятием множества вершин именно нулевого цвета.

Совершенным кодом (с расстоянием 3) называется такое подмножество вершин графа, что любая вершина графа либо является кодовой, либо находится на расстоянии 1 в точности от одной кодовой вершины. Совершенный код в d-регулярном графе является полностью регулярным, и матрица параметров соответствующей дистанционно регулярной раскраски имеет вид [0d — 1d— 1].

Цель данной статьи - найти все дистанционно регулярные раскраски в бесконечном графе треугольной решетки, а значит, и все полностью регулярные коды в ней. Определим треугольную решетку как граф Кэли коммутативной группы с множеством образующих S = {х, у, z, х^-1, у^-1, z ¹} с определяющим соотношением xyz = е, где е обозначает единичный элемент группы. Вершинами этого графа являются элементы группы, причем каждая вершина v смежна, со следующими шестью вершинами: x v , x^-i v , yv, y^-iv,zv, z^-1v. Таким образом, это регулярный граф степени 6. Приведем фрагмент графа, треугольной решетки:

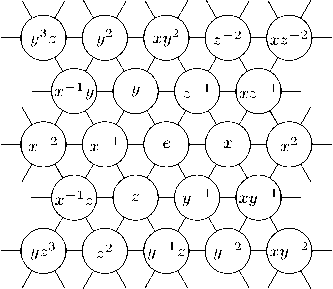
У z

*

В дальнейшем на рисунках ребра будем опускать, и при последовательном раскрашивании вершин графа на месте обозначения вершины обычно будем писать ее цвет, а индекс будет соответствовать номеру шага, на котором фиксируется цвет вершины. Линией назовем множество вершин решетки, отличающихся лишь степенью одной образующей, т.е. множество {w^mv : m Е Z}, гд e v - некоторая вершина треугольной решетки, aw € {ж, у, 2} -некоторая образующая.

Граф треугольной решетки накрывается графом трехмерной квадратной решетки, и при этом каждая вершина с координатами (а, Ь, с) трехмерной квадратной решетки отображается в вершину х^ау^ъх^с треугольной решетки; нетрудно видеть, что это отображение сюрьективно и сохраняет смежность вершин.

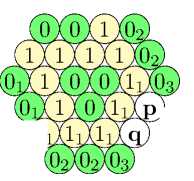
Аналогично квадратной решетке (двумерной или большей размерности), треугольная решетка не является дистанционно регулярным графом. Определение дистанционно регулярного графа в наших терминах выглядит следующим образом: код, состоящий из одной (произвольной) вершины графа, является полностью регулярным, т.е. раскраска по расстоянию от этой вершины является дистанционно регулярной. В случае же треугольной решетки это условие нарушается: как видно на следующем рисунке,

(зазазАз) (зццхцз) хзцхтеща! зйимш з®55лчЖ ^ЖІЙХІХз)

(ЗҮзТзҮз)

вершины второго цвета имеют разное число соседей первого цвета1.

• 2.    Редуцируемость дистанционно регулярных раскрасок

Раскраску вершин треугольной решетки будем называть редуцируемой, если найдется образующая, такая что любые две вершины, различающиеся лишь степенью этой образующей, имеют одинаковый цвет (например, это образующая ж и для любых а, Ь, с, г Е Z цвета вершин х^ау^ъх^с и х^а+гу^ъz^c совпадают). Полностью регулярный код С будем называть редуцируемом, если дистанционная раскраска (Vq = С, V1, ... , V&—1) относительно него является редуцируемой. Нетрудно понять, что для произвольного к > 3 существуют ровно три неэквивалентных редуцируемых дистанционно регулярных раскраски в к цветов:

Цветное изображение иллюстраций данной статьи см.

Их матрицы параметров, соответственно, следующие:

[24-222- ... -222-42],     [24-222- ... -222-24],     [42-222- ... -222-24].

Для числа цветов к = 2 также существует три неэквивалентных редуцируемых дистанционно регулярных раскраски, мы упомянем их в разделе 5 вместе с другими раскрасками в два цвета.

Редуцируемые раскраски описаны, теперв рассмотрим нередуцируемые.

Теорема 1. Пусть (Vq, V1, ... , V^-i) - нередуцируемая дистанционно регулярная раскраска треугольной решетки. Тогда к < 3.

Доказательство. Предположим обратное, т.е. что ( V 0 , V i ,..., V ^—i) - нередуцируемая дистанционно регулярная раскраска треугольной решетки и к > 4. Это означает, что найдется цепь из четырех вершин, имеющих различные цвета 0, 1, 2 и 3. Здесь и везде далее проводим рассуждения с точностью до симметрий треугольной решетки. Возможны только следующие варианты такой цепи с точностью до эквивалентности:

Из представленных вариантов четвертый приводит к противоречию: вершина v должна иметь цвет не более 1 и не менее 2. Третий вариант сводится ко второму, поскольку вершина u однозначно раскрашивается в цвет 2. Таким образом, осталось рассмотреть два случая.

Напомним, что на рисунке в вершине мы записываем ее цвет, а индекс указывает на номер шага, на котором эта вершина будет окрашена. Последовательно раскрашивая вершины графа, руководствуемся следующими соображениями. Во-первых, цвета смежных вершин отличаются не более чем на единицу, это следует из дистанционной регулярности раскраски. Во-вторых, если окрестность некоторой вершины уже раскрашена полностью, то любая вершина одного с ней цвета должна иметь тот же цветовой состав окрестности, поскольку наша раскраска совершенна.

Пусть раскраска такова, что есть цепь из четырех вершин, имеющих различные цвета 0, 1, 2 и 3, первого типа. Тогда вершины u и v могут быть раскрашены в цвета 0 или 1:

Сначала пусть они обе - цвета 0. Однозначно продолжаем:

0 11 22 0123

0 11 22

При этом получили в нашем фрагменте вершины цвета 1, имеющие различное число соседей цвета 2, противоречие.

Если обе вершины u и v имеют цвет 1, то ситуация аналогична.

Остался вариант, когда одна из этих вершин нулевого цвета, а другая - первого. Без ограничения общности считаем, что u имеет цвет 0, a v - цвет 1, и продолжим раскраску: ···    ···

01 11 21 32

00 10 20 30

02 11 21 31

03 12 22 32

04 13 23 33

Получаем раскраску бесконечного фрагмента графа (полосы), состоящую из одноцветных линий. Нетрудно понятв, что любое продолжение раскраски этого фрагмента до дистанционно регулярной раскраски всей треугольной решетки окажется редуцируемым.

Теперь рассмотрим случай, когда дистанционно регулярная раскраска имеет не менее четырех цветов, причем любая цепь из четырех вершин, имеющих цвета 0, 1, 2 и 3, второго типа.

3 012

Продолжим раскраску:

s 11 21 3 012t

Если здесь вершина s имеет цвет 0 или вершина t имеет цвет 3, то такой случай мы уже рассмотрели. Поэтому полагаем, что s - цвета 1, a t - цвета 2. Рассмотрим следующие вершины u II v. из которых u может быть первого или второго тщета, a v - второго пли третьего:

uv

12 11 21 3 0 1 2 22

Пусть сначала вершина u - цвета 1, а вершина v - цвета 2. Тогда приходим к противоречию, так как при любом цвете вершины w есть две вершины первого цвета с различным числом соседей второго цвета:

w 13 23

12 11 21 3 0 1 2 22 ,х ,х х х ■

Пусть теперь обе вершины u и v имеют цвет 2. Тогда, аналогично, приходим к противоречию, поскольку в нашем фрагменте найдутся две вершины цвета 2, имеющие разный цветовой состав окрестности:

14 24

04 23 23

12 11 21 3

0 1 2 22

Пусть, наконец, вершина u - цвета 2, вершина v - цвета 3. Тогда смежные вершины q и r невозможно раскрасить непротиворечиво, поскольку одна из них должна быть первого цвета, а другая - третьего:

23 33

12 11 21 3

0 1 2 22 qr ■

Таким образом, только в одном случае дистанционно регулярная раскраска существует, но она является редуцируемой. Теорема доказана.

• 3.    Основной результат

Из теоремы 1 следует, что для поиска всех дистанционно регулярных раскрасок треугольной решетки достаточно проверить матрицы параметров порядка 2 и порядка 3, удовлетворяющие условию, что сумма элементов каждой строки равна 6.

Теорема 2. Все. матрицы параметров дистанционно регулярных раскрасок треугольной решетки исчерпываются следующим списком:

• а)    десять матриц порядка 2: [06-15], [06-24], [06-33], [15-24], [15-33], [24-24], [24-33], [24-42], [33-33], [42-24];

• Ь)    шесть матриц порядка 3: [24-222-42], [24-222-24], [42-222-24], [06-123-24], [06-123-33], [06-132-60], [06-141-60];

• с)    для каждого к > 4 три матрицы порядка к:

• [24-222- ... -222-42], [24-222- ... -222-24], [42-222- ... -222-24].

• 4.    Дистанционно регулярные раскраски в три цвета

Для каждой из матриц [06-24], [15-33] и [24-42] существует бесконечно много неэквивалентных дистанционно регулярных раскрасок; для каснсдой из матриц [24-24] и [24-33] существуют в точности две неэквивалентные дистанционно регулярные раскраски; для каждой из остальных матриц существует единственная с точностью до эквивалентности дистанционно регулярная раскраска.

Доказательство этой теоремы проводится в последующих двух разделах 4 и 5, в которых рассматриваются раскраски в три и два цвета соответственно. Для этого производится перебор всех возможных матриц параметров раскрасок. Рассматривая матрицу, будем либо доказывать, что раскраска с такими параметрами не существует, либо строить все соответствующие раскраски. При построении раскрасок начинаем с некоторого небольшого фрагмента (чаще всего это некоторая вершина и ее окрестность) и продолжаем ее, если это возможно сделать однозначно. Если возникает неоднозначность, рассматриваем каждый из вариантов (либо указываем на их эквивалентность). Почти все раскраски, восстанавливающиеся однозначно по начальному фрагменту, будут периодическими, и число шагов построения фрагмента раскраски будем выбирать так, чтобы эта периодичность была обнаружена. Единственная, однозначно восстанавливаемая, но непериодическая, встретится среди раскрасок в два цвета с матрицей параметров [24-42]; для нее однозначность продолжения будет очевидна. Для некоторых матриц параметров имеется бесконечно много дистанционно регулярных раскрасок, для них будем указывать однозначно восстанавливаемые фрагменты и способы «склеивания» таких фрагментов.

Нам надо рассмотреть все трехдиагональные матрицы порядка 3 с элементами из множества {0,1, 2, 3,4, 5, 6}, у которых сумма элементов любой строки равна 6. Упорядочим их по тому, какой вид имеет средняя строка. Предварительно установим, что некоторые варианты средней строки не могут встречаться в матрицах дистанционно регулярных раскрасок треугольной решетки:

Лемма 1. Пусти Vo, V1, V2 - дистанционно регулярная раскраска в три цвета с матрицей параметров А = [000 001-010 011012 -021 022]. Тогда 011 > 2.

Доказательство. Поскольку имеем раскраску в три цвета, то окрестность произвольной вершины цвета 1 обязательно содержит вершины и цвета 0, и цвета 2. Но эта окрестность представляет собой цикл, а вершины цвета 0 не могут быть смежны с вершинами цвета 1. Значит, этот цикл содержит, по крайней мере, две вершины цвета 1. Лемма доказана.

Таким образом, существует четыре варианта для средней строки (010, 011,012) матрицы параметров дистанционно регулярной раскраски треугольной решетки в три цвета:

(1,4,1), (1, 3, 2), (1, 2, 3), (2, 2, 2).

Варианты (2, 3,1) и (3, 2,1) отдельно рассматривать не будем, поскольку они получаются центральной симметрией из указанных.

[... -141- ...].

Предположим, что окрестность любой вершины цвета 1 имеет следующий вид:

UD1 уТО Т0Ү1Т

*

Но тогда вершину v невозможно раскрасить с сохранением этого условия:

UDI

ToY1Yv

Значит, встретится вершина первого цвета с окрестностью вида

UDI

Т1Ү1У

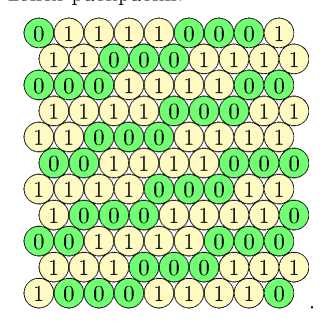
Попробуем продолжить эту раскраску до раскраски всего графа:

,д8ц8цал28х1§и Д18ц7итц7ц7ц§и

(мытуиХЖд^ мммоХтМЫмм (18w)^lDГ^[Гx^^

CI8D6X13D3D3D (мрзіиііДиі^ц^ *^8s7s7^t^Ds8 (ымыъш

Легко видеть, что раскраска периодична и восстанавливается однозначно, причем ее матрица параметров есть

[06-141-60].

В этой раскраске вершины нулевого и второго цветов образуют следующие полностью регулярные коды:

Vo = {UVW" :т,п G Z},   V2 = {(D,    /   : т.п G Z}.

[ ...- 132 -... ] .

Предположим, что в нашей раскраске окрестность некоторой вершины первого цвета имеет следующий вид:

Достраивая раскраску, получаем:

(1Д2)

< 2Д2 ДуГ т.е. вершины u и v должны иметь цвета 0 и 1, но они обе смежны с вершинами цвета 2, т.е. приходим к противоречию. Поэтому окрестность любой вершины цвета 1 имеет такой вид:

У1Х2У

Достраиваем раскраску:

У17л7ц7^17л7ДтУ

У^Тцбцб^бцбцб^ТУ (л&бдіддцд&аій уліідіхйаіціХй *279659!29Д5®8д6дК

• * М16®23№д2д1^^

Улдбцдыйш

• У дТлб^рУХ¹^

• У &цбдбдбдбцб^уУ УУУ ТХлдУ УуУу

Легко видеть, что такая раскраска периодична, и на каждом последующем шаге будет однозначно определяться цвет вершин, находящихся на расстоянии 1 от множества уже раскрашенных. Такая раскраска существует и единственна, причем ее матрица параметров есть

[06-132-60].

В этой раскраске вершины нулевого и второго цветов образуют следующие полностью регулярные коды:

По = {х^3ту^3п : т,п Е Z}, П = {(ху^-1)х^3ту³Д (xz^-1)х^3ту^3п : т,п Е Z}.

[...-123- ...].

При данной средней строке матрицы параметров вид окрестности любой вершины цвета 1 определен однозначно; достроим ее до шара радиуса 2:

У1Ү2У

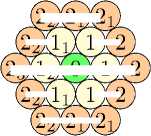
2оП

1 1 2

2»И

1 1 2

2»Г2 2

23 ІЫ01112

♦

Таким образом, сферы радиуса 1 и 2 с центром в произвольной вершине цвета 0 целиком окрашены в цвета 1 и 2 соответственно. Получаем, что в матрице параметров раскраски однозначно определилась нулевая строка, (аоо, ао1, ао2) = (0, 6, 0), и каждая вершина цвета 2 смежна не менее чем с двумя вершинами цвета 1, и не менее чем с двумя вершинами цвета 2, т.е. а21 > 2 и 022 > 2. Поэтому надо рассмотреть три варианта последней строки матрицы параметров: (а2о, а21, а22): (0, 4, 2), (0, 3, 3) и (0, 2,4).

[06-123-42].

Продолжаем раскраску:

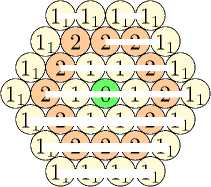
1 1

2X2X1

1 1

2Х1Х1Х2Х1

2Ш0Ш2П

Ы 2X1X1 Х2Х11

111 2Х2Х2ХП

*

Легко видеть, что сферу радиуса 4 с центром в произвольной вершине цвета 0 невозможно раскрасить с соблюдением условия аіо = 1, получили противоречие.

[06-123-33].

Рассмотрим выделенные вершины и и v:

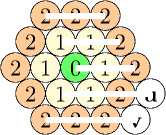
2X2X2

1X1X2

0X1X2

1X1X2 Хи

2X2X2X v

*

Ровно одна из них должна быть окрашена в цвет 2, а вторая - в цвет 1. В силу симметрии без ограничения общности положим, что вершина и второго цвета, и однозначно продолжаем раскраску:

(14X2112X12)

2555Х15ДХ 03>®$@@Ч0 цбЗХиЗІХІХ ыЖЕіТ)

ЦзХЦХ^ХХй)

1мммыым Хд32®№ /450X315131312^ (251X1323255^ 6X531X51555X5^ 2X1X52555555322 5Х53555525з2Х QXX555551X3 555555Ж5 (235м131355

Легко видеть, что далее раскраска однозначно периодически продолжается на всю треугольную решетку. Цвет 0 и цвет 2 образуют следующие полностью регулярные коды:

По = {(x³z^-1 )^т(у³х^-1Ц : m,n G Z}

V2 = {х² V , х ² v ,y² v , у 2 v ^² v, z ² v : v G По}.

[06-123-24].

В силу вида средней строки матрицы параметров, имеем шар радиуса 2 с центром в вершине нулевого цвета, раскрашенный по расстоянию от центра. Продолжаем раскраску:

14 14 24 24 14 14

14 03 13 23 13 03 14

24 13 12 21 21 12 13 24

24 23 21 2 2 2 21 23 24

14 13 21  2  1  1  2  21 1314

14 03 12 2  1  0  1  2 1203 1

14 13 21  2  1  1  2  21 1314

24 23 21  2  2  2 21 2324

24 13 12 21 21 12 13 24

14 03 13 23 13 03 14

14 14 24 24 14 14

Легко видеть, что далее раскраска однозначно периодически продолжается на всю треугольную решетку. Таким образом, получаем, что цвет 0 и цвет 2 образуют следующие полностью регулярные коды:

По = {_ж^т_у^п : т,п G Z},      V2 = {х²у^п, y²zⁿ, z²zⁿ : п G Z}.

[... -222-...].

В этом случае в нашей раскраске окрестность любой вершины первого цвета имеет следующий вид:

Тогда однозначно восстанавливается раскраска бесконечной полосы:

05 04 03 02 01 0 0 01 02 03 04 05

15 14 13 12 11 1 1 1 11 12 13 14 15

25 24 23 22 21 2 2 21 22 23 24 25

Поскольку раскраска дистанционно регулярна, то любое продолжение этого фрагмента будет редуцируемым, и такие раскраски были рассмотрены ранее.

• 5.    Дистанционно регулярные раскраски в два цвета

Сначала, для сокращения перебора, докажем лемму:

Лемма 2. Если существует дистанционно регулярная раскраска в два цвета с матрицей параметров [000001-15], то это - матрица [06-15].

Доказательство. Предположим, что такая раскраска существует. Рассмотрим произвольную вершину первого цвета и ее окрестность, и продолжим раскраску:

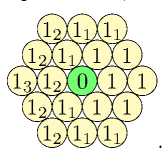
12 11 11

12 11 1 1

13 12 0 1 1

12 11 1 1

12 11 11

Очевидно, что тогда матрица параметров имеет вид [06-15]. Лемма доказана.

Далее будем действовать перебором всех матриц параметров А = [000001 - 010011], для которых выполнено условие 000 + 001 = 010 + оц = 6.

[06 - ... ] .

Так как любая вершина из окрестности произвольной вершины смежна с двумя другими вершинами из этой же окрестности, то из условия oqq = 0 (т.е. в окрестности любой вершины нулевого цвета все вершины имеют цвет 1) следует, что ац > 2. Значит, для матриц [06-51] и [06-60] дистанционно регулярных раскрасок не существует, и требуется рассмотреть только следующие варианты матрицы А:

[06-42],      [06-33],      [06-24],      [06-15].

[06-42].

Поскольку аю = 4, в окрестности каждой вершины цвета 1 имеется ровно четыре вершины цвета 0, но тогда некоторые из них обязательно окажутся смежными, что противоречит условию аоо = 0. Значит, дистанционно регулярных раскрасок с такой матрицей параметров не существует.

[06-33].

Поскольку ащ = 3, в окрестности каждой вершины цвета 1 имеется ровно три вершины цвета 0, но при этом аоо = 0, т.е. они не смежны, а значит, окрестность любой вершины цвета 1 имеет следующий вид:

$шг Х55

Продолжаем раскраску:

д12^12^2Д5 ЛдодыЖ) ДмыЦоЫУ 125555До$1 оЖ51$01х ХыоДыыоХ дідодід

Очевидно, что раскраска периодическая и далее однозначно продолжается на вето треугольную решетку, причем ее цвета образуют полностью регулярные коды Vq и V i = L \ Vq, где

V₀ = {ж^3т(ж 1y)ⁿ : m, ri Е Z}.

[06-24].

В этом случае окрестность любой вершины цвета 1 может быть одного из следующих двух типов:

Т55

ХоШ 955 Х55

Сначала предположим, что раскраска такова, что окрестность любой вершины первого цвета - первого типа. Тогда однозначно восстанавливается раскраска следующего фрагмента:

12 02 12 02 12

12 12 11 11 12 12

12 02 11 01 11 02 12

12 12 11 1 1 11 12 12

12 02 11 0 1 0 11 02 12

12 12 11 1 1 11 12 12

12 02 11 01 11 02 12

12 12 11 11 12 12

12 02 12 02 12

а затем она периодически продолжается на всю треугольную решетку. Структура этой раскраски такова, что вдоль каждой образующей чередуются линии, полностью окрашенные в первый цвет, и линии, в которых идет чередование вершин нулевого и первого цветов. Полностью регулярный код, состоящий из вершин нулевого цвета этой раскраски, описывается следующим образом:

Р0 = {ж^2т у^2п : т,п Е Z}.

Если же найдется вершина цвета 1 с окрестностью второго типа, тогда однозначно восстанавливается бесконечная полоса:

15 15 13 13 11 11 12 13 15 15

15 04 13 02 11 0 1 02 13 04 15

15 15 13 13 11 1 1 1 13 13 15 15

15 04 13 02 11 0 1 02 13 04 15

15 15 13 13 11 11 13 13 15 15

Нетрудно видеть, что эту полосу можно получить из соответствующей полосы предыдущей раскраски инвертированием цветов вершин одной линии, в которой цвета вершин чередуются. Таким образом, любая раскраска будет состоять из бесконечных полос вида

Тогда полностью регулярный код Т0 с данными параметрами будет описываться следующим образом:

По = J {ж2т+-^у2п : т,и Е Z}, nez где еп Е {0,1}, п Е Z, - произвольные числа, отвечающие за сдвиги полос.

[06-15].

Любая вершина цвета 1 смежна в точности с одной вершиной цвета 0, и вершины цвета 0 не смежны. Это означает, что множество По вершин цвета 0 является совершенным кодом. Такой код в треугольной решетке единственен с точностью до изоморфизма. Построим его. В следующем фрагменте

11 1 0 1 11

11 1 1 11

11 11 11

в точности одна из вершин u, v должна быть окрашена в цвет 0; без ограничения общности положим, что это - вершина v, и продолжим раскраску. На каждом шаге цвет вершин выбирается однозначно:

/ДбДбДбд діб&дібдібі „ д6Ц5Х05ХіІЦ2Хі2і

ХшДДдОдЗОйк №Ш1Ы№ дмишш1зц4^^ іДыжі^&ЗдзЦ^^ ДбДі&іЙ^д^д^

ДбДбДб)

Очевидно, что раскраска периодична и далее восстанавливается однозначно. Тогда этот полностью регулярный код ТО, являющийся совершенным, будет описываться следующим образом:

То = {(ж^-1у²)^тСг^-1ж²Г : m,n G Z}.

[15 -... ] .

Поскольку ago = 1, то для любой вершины цвета 0 есть еще одна, смежная с ней, имеющая цвет 0. Рассмотрим такую пару вершин, без ограничения общности можем считать, что они различаются по образующей ж. Аналогично предыдущему случаю, в окрестности произвольных смежных вершин цвета 0 все вершины имеют цвет 1, а эта окрестность -цикл, и потому аң > 2:

ш0ж® (ГШы ----•

Кроме того, видим, что некоторые вершины цвета 1 смежны не менее, чем с двумя вершинами цвета 0, а значит это верно для всех вершин цвета 1, и aio > 2. Значит, для матриц [15-15] , [15-51], [15-60] соответствующих дистанционно регулярных раскрасок не существует, и потому требуется рассмотреть следующие варианты матрицы параметров:

[15-42],      [15-33],      [15-24].

[15-42].

Вследствие условия aio = 4 получаем

М01ЖЖ лД5®ш0К 015л0Ж®01 <01ш®ш0т (0 1фд0д01Г

Но это противоречит условию ago = 1, поэтому не существует дистанционно регулярных раскрасок с такой матрицей параметров.

[15-33].

Начиная строить раскраску, видим, что из вершин u, v ровно одна должна быть окрашена в цвет 0, а вторая - в цвет 1, и аналогичное верно для пары вершин s, t:

111 1001 111 TuYvT

Достаточно рассмотреть два типа пары смежных вершин нулевого цвета: во-первых, когда вершины u н s - цвета 0. a. v и t - цвета 1: іі во-вторых. когда вершины u ii t цвета. 0. а. v II s - цвета. 1:

111 0 1

(Оставшиеся еще два случая получаются из указанных симметрией решетки.) Соответсвующие этим случаям однозначно восстанавливаемые фрагменты раскраски представлены ниже:

1 4 1 4 0 5

1 4 0 3 1 2 1 2

1 4 0 1 0 1 1 2

05  1  1  1  01 12

16 1 0 0 1 12 06

05  1  1  1  01 12

1 4 0 1 0 1 1 2

1 4 0 3 1 2 1 2

1 4 1 4 0 5

0 5 1 4 1 4

1 2 1 2 0 3 1 4

12 01 1 0 13

12 01  1  1  1  03

12 1 0 0 1 12

0 5   1  1  1 0 1 1

1 4 0 1 0 1 1 2

1 4 0 3 1 2 1 2

1 4 1 4 0 5

Для наглядности изобразим эти фрагменты следующим образом, опуская вершины первого цвета:

Сначала, предположим, что раскраска, такова, что любая пара, смежных вершин цвета. 0 -первого типа. Тогда, однозначно восстанавливаем раскраску всей треугольной решетки с точностью до изоморфизма:

регулярный код Р0

этот полностью

*

Нетрудно видеть, что следующего вида:

состоит из бесконечных полос

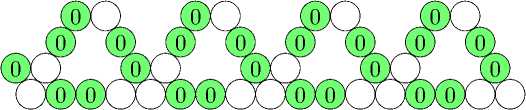
и в каждой из них есть линия, в которой вершины нулевого и первого цветов чередуются.

Теперь рассмотрим произвольную раскраску, в которой встретится второй тип пары смежных вершин нулевого цвета. Аналогичным образом проводя постоения, видим, что однозначно восстанавливается бесконечная полоса:

03 03        01 0         01 01

03           01            0            01

03    02    01     0     0     01    02

02            0            00

02 02        0 00

02            0            00

03    02    01     0     0     01    02

03           01            0            01

03 03        01 01         0 01

Нетрудно видеть, что эту полосу можно получить из соответствующей полосы предыдущей раскраски инверсией цветов вершин одной («горизонтальной») линии, в которой цвета вершин чередуются.

Таким образом, любая раскраска будет состоять из бесконечных полос двух следующих типов, различающихся инверсией цветов одной линии:

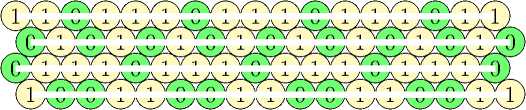
Полностью регулярный код V0 с данными параметрами описывается следующим образом:

По = {_ж^4т+1у⁴ф _Ж^4т+У^и : т,п Е Z} и{ж^4ту^4п+1 : т,п Е Z} J U{^^2m+e"у^4п+2 : т, п Е Z} J{^^4m-1y⁴ⁿ⁺3 : т,п Е Z}, где е_п Е {0,1}, п Е Z, - произвольные числа, отвечающие за сдвиги полос.

[15-24].

При такой матрице параметров окрестность произвольной вершины цвета 1 может быть одного из следующих трех типов:

11 010

причем поскольку аоо = 1, то вершины первого цвета с окрестностью третьего типа встречаются в каждой раскраске с данными параметрами. Однако очевидно, что не не существует раскраски с такими параметрами, в которой окрестность любой вершины первого цвета именно третьего типа. Предположим сначала, что в нашей раскраске окрестности вершин первого цвета - только первого и третьего типа, тогда продолжаем раскраску:

11 11 11

02 11 0 0 11 02

12 1 1 1 12 u11v видим, что вершины u и v должны быть раскрашены в цвет 0, но тогда две вершины «между ними» имеют цвет 1 и их окрестности будут второго типа. Значит, найдется вершина первого цвета с окрестностью второго типа. Рассмотрим эту вершину и продолжим раскраску:

11 11

11 1 0

011 q 11

Ясно, что в точности одна из вершин р и q должна иметь цвет 0, без ограничения общности положим, что эта вершина - р. Продолжаем раскраску. В точности одна из вершин s и t должна иметь цвет 0:

11 1 1 s

11 1 1 0 t

11 0 0 1 1

11 1 1 1

11 11 01

Положим сначала, что эта вершина - s. Тогда, раскрашивая граф далее, видим, что вершина w не может быть окрашена без противоречий с параметрами:

w 11 11

1 1 1 0 11

Значит, вершина s имеет цвет 1, а вершина t - цвет 0. Тогда продолжаем:

17 15 13 13 13 04 08

17 15 13 02 02 11 11 18

17 06 04  1  1  1  1  1108

17 15  1  1  1  0  0  1117

17  1  0  0  1  1  11 1517

08  1  1  1  1  11 0406 17

18  1  1  0 02 13 1517

08 04 13 13 13 15 17

Дальнейшее продолжение однозначно в силу периодичности и

То = {(_ж^-1у²)^т(_г^-1_ж²)^и, _Ж(_Ж^-1у²)^тД^-1ж2Г : m,n G Z}.

Заметим, что в этой раскраске множество вершин нулевого цвета - это двукратный совершенный код, полученный объединением совершенного кода и его смежного класса. (Совершенный код ранее был получен как множество вершин нулевого цвета дистанционно регулярной раскраски с параметрами [06-15].)

[24 -... ] .

Матрицы [24-60] и [24-51], с точностью до центральной симметрии, были рассмотрены ранее. Для матрицы параметров [24-15] дистанционно регулярная раскраска не существует вследствие леммы 2, и осталось рассмотреть матрицы параметров

[24-24],      [24-33],      [24-42].

[24-24].

Окрестность произвольной вершины нулевого цвета может быть одного из следующих трех типов:

11 000

Сразу видим, что в случае второго типа окрестности имеется вершина первого цвета, смежная с тремя вершинами нулевого цвета, что противоречит параметрам раскраски. Значит, возможны лишь первый и третий типы окрестностей. Сначала пусть раскраска такова, что имеется вершина цвета 0 с окрестностью первого типа. Тогда

12 11 11 11

12 11 0 1 11

11 0 0 1 v

11 1 1 u

11 11

и ровно одна из вершин u и v должна иметь цвет 0, сначала положим, что эта вершина -u. Продолжая раскраску, приходим к противоречию - вершину w невозможно раскрасить в соответствии с параметрами:

1111 11011w

1 0 0 1 1 13

1 1 1 0 02 13

1 1 11 02 13

13 13

Поэтому вершина v должна иметь цвет 0. Тогда продолжаем:

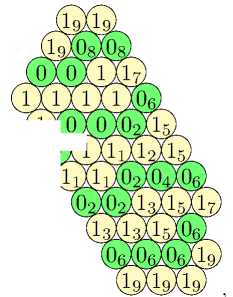
18 18 09 18 18

07 16 05 05 16 07

1  1  1  1  14 1415

1  1  0  1  1 03 1415

06 1  0  0  1  0 03 1407

17 15  1  1  1  1  12 14 1618

17 04  1  1  01 12 13 0518

08 04 13 02 02 13 05 09

17 15 13 13 13 16 18

17 06 14 14 07 18

Получаем однозначное восстановление раскраски всей треугольной решетки в силу периодичности. Вершины нулевого цвета этой раскраски образуют следующий полностью регулярный код:

По = {_ж^3ту³ф _ж^3т-1у^3и, _ж³"У^и+1 : т,п G Z}.

Теперь предположим, что раскраска такова, что любая вершина нулевого цвета имеет окрестность третьего типа. Тогда любая компонента связности множества ПО вершин цвета 0 представляет собой бесконечную цепь следующего вида:

€@®®оХоХ0@@@@@@@@.

Поэтому единственной раскраской, удовлетворяющей и параметрам, и условию на окрестности вершин нулевого цвета, будет следующая редуцируемая:

111111111111111 00000000000000 111111111111111 11111111111111 000000000000000 11111111111111 111111111111111 00000000000000 111111111111111

Формула для полностью регулярного кода ПО здесь очевидна.

[24-33].

Окрестность произвольной вершины цвета 1 может быть одного из следующих трех типов:

Сначала рассмотрим раскраски, в которых есть вершина первого цвета с окрестностью первого типа. Тогда в точности одна из вершин u, v и w имеет цвет 1:

01u

110v

01w

Пусть это вершина v. Выписывая этот фрагмент и затем раскрашивая соседние вершины в соответствии с параметрами, приходим к противоречию в вершине t:

ДоДтдоу ТХиМТ ТоТТТоУ

1од	од	тдоддодУзд
	ХТ	жПыоЖ
ДУД	S	1ЖЫ№^
дзЖ	21 1	Иу^зИзфХ

ДзДзЖДб/Д.

*

Поэтому заключаем, что вершина v нулевого цвета, а первого цвета - одна из вершин u и w, без ограничения общности можем считать, что это вершина u. Приведем исходный фрагмент для раскраски и продолжим ее однозначно, пока это возможно.

ДоИДТ! ТХТ®$ 'ГоУтХоУ

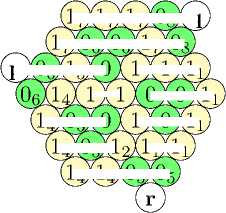
ШД1

оходп иодт

11ДТ

14Л1ДОбАо5

1 1 1

¹41 ОзД О

14АозД1

r

17 Д17ДІ7Д^о8 q

17АобЛобДІ7Ао8

p Д^об1151 °

*

Покажем, что три отмеченные вершины, p , q и r имеют цвет 0. Для этого предположим, что вершина p - тщета 1. Продолжая, придем к противоречию в вершине s:

(1д1д1додд) ууЗХХХХуХХОХ (Ы№ХоИЖ

(обЫозЫМ^ (ддДТЙШШд) (ГХуХоХоУ

r

Значит, вершина p имеет цвет 0. Аналогично рассматриваются вершины q и г. Таким образом, все три вершины p , q и r имеют цвет 0. Далее раскраска восстановится однозначно в силу периодичности:

Шо чМшомм

■ЗдОХОХХХу дУадиЖоИодДЫ ыДСохтХодХтлПм ДтХдХТ^

'уДйоХоХтйКдУ 52ш$1д@®оД УмииоХодуУ

УоДсУдДД^ УДДзХХДв)

Получили полностью регулярный код

По = {(_ж^-1у²)^т(.г^-1_ж²)Д _Ж(_Ж^-1у²)^т(.г^-1_Ж²р, у^-1(ж^-1у²)^т(г^-1ж²)^п : m,n G Z}, который является объединением трех смежных классов совершенного кода, причем найдутся представители этих смежных классов, е,ж и у^-1, попарные расстояния между которыми равны 1.

Осталось рассмотреть раскраски, в которых нет вершин первого цвета с окрестностью первого типа. Пусть теперь есть вершина первого цвета с окрестностью второго типа. Тогда среди вершин u , v и w

доДоХид иии® Tu®WX либо вершина u, либо вершина w имеет цвет 0, поскольку иначе появится вершина первого цвета с окрестностью первого типа. Предположим, что именно вершина u нулевого цвета. Продолжим раскраску, соблюдая наше условие на окрестности вершин первого цвета. Тогда четыре вершины нижнего ряда невозможно непротиворечиво раскрасить в соответствии с параметрами [24-33]:

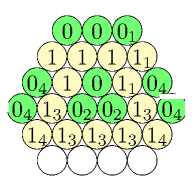
доДоЖД

ДмиоХыоД ицДоХбзДЗЖ 4Д3ДзИзЦу

Это означает, что нулевого цвета должна быть вершина w. Теперь видим, что в точности одна из вершин s и t имеет цвет 0:

ДоДоДи

ХГ©®' st

Пусть вершина s имеет цвет 1, а вершина t - цвет 0. Продолжаем, учитывая условие на окрестности вершин первого цвета:

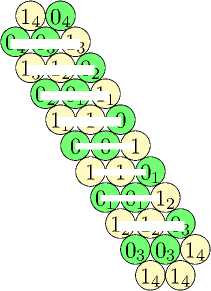
доДоДиоз) ©Хиии® мГ@©Ж Ходи®®© иХДгД

Вершины p и q не раскрашиваются в соответствии с параметрами, значит, вершина, s имеет цвет 0, а вершина t - цвет 1. Приведем начальный фрагмент с раскрашенными таким образом вершинами s и t, затем продемонстрируем несколько шагов дальнейшего однозначного раскрашивания и затем - более крупный фрагмент получившейся раскраски:

дододи ииид Хи®© (оГГ)

оидиииодододи Хиш©оХоХдХдХид оХЙоХГШииоХ® ЖПШоМоЖ uu©®®©®®© бХоХииииоХоХо иииХХох®®®© Хи®оХ®®Ш®© ииииии®®© ХииГХоХоХоХ1Хи1 иоТоГоХииии®'

ДоДоДиьД шшГж иоДожад

ХДиХДо Т^еД фДоДз®®

АзМздДдОб

МДА

Получим полностью регулярный код из вершин нулевого цвета, не эквивалентный найденному ранее:

По = {(ж^-1у²)^т(.г^-1_ж²р, ж(ж^-1 у²)™^^-1^)", ж²(ж^-1у²)^тД^-1ж²Г : т,п G Z}.

Он также получен объединением трех смежных классов по совершенному коду, но в данном случае не найдется таких трех представителей этих классов, что все попарные расстояния между ними были бы равны 1.

[24-42].

Так же, как при рассмотрении матрицы [24-24], рассмотрим окрестность произвольной вершины нулевого цвета. Она может быть одного из следующих трех типов:

11 000

Пусть сначала раскраска такова, что в ней есть вершина нулевого цвета первого типа. Начиная с нее, однозначно восстановим раскраску треугольной решетки:

15 04 04 04 04 04 15

15 04 13 13 13 13 04 15

15 04 13 02 02 02 13 04 15

15 04 13 02 11 11 02 13 04 15

15 04 13 02 11  0  1 02 13 04 15

15 04 13 02 11 0 0 1 02 13 04 15

15 04 13 02 11  1  1 02 13 04 15

15 04 13 02 02 02 02 13 04 15

15 04 13 13 13 13 13 04 15

15 04 04 04 04 04 04 15

*

Описание полученного полностью регулярного кода V0 очевидно.

Инвертируя цвета, получим другую, эквивалентную исходной, дистанционно регулярную раскраску.

Значит, во всех остальных раскрасках с данными параметрами нет трех соцветных попарно смежных вершин. Тогда любая компонента связности множества V0 вершин нулевого цвета и любая компонента связности множества V вершин первого цвета является бесконечной простой цепью. В частности, если любая вершина нулевого цвета обладает окрестностью третьего типа, то раскраска единственна:

111111111111111 000000000000000 111111111111111

Соответствующий вершинам нулевого цвета полностью регулярный код есть

V = {x^my^2Tl : т, п Е Z}.

Отметим, что в этой раскраске в любой цепи вдоль одного из направлений цвет вершин постоянен, а в любой цепи вдоль любого из двух оставшихся направлений вершины нулевого и первого цветов чередуются.

Если в раскраске имеется вершина нулевого цвета с окрестностью второго типа, то восстанавливается бесконечная полоса, пересекающая все компоненты связности обоих цветов:

04 03 13

13 12 02

02 01 11

11 1 0

12 12 03

*

Таким образом, любая дистанционно регулярная раскраска с параметрами [24-42] состоит из «параллельных» бесконечных простых цепей. Приведем пример:

0000101010111010000 1111010101000101111

0111101010100010111 1100001010101110100

0011110101010001011 1110000101010111010

0001111010101000101 1111000010101011101

Нетрудно видеть, что любая такая раскраска может быть получена из предыдущей раскраски инвертированием цветов вершин в произвольном множестве цепей вдоль некоторого направления, и поэтому

Т = {жту2п+ет : т, п G Z}, где ет G {0,1}, т G Z, - произвольные числа, отвечающие за сдвиги полос.

[33 - ... ] .

Матрицы [33-60], [33-51] и [33-42], с точностью до центральной симметрии, были рассмотрены ранее. Для матрицы параметров [33-15] дистанционно регулярная раскраска не существует вследствие леммы 2. Осталось рассмотреть матрицы параметров

[33-24],      [33-33].

Окрестность произвольной вершины цвета 0 может быть одного из следующих трех типов:

100 01

101 01

[33-24].

В искомой раскраске ни одна вершина нулевого цвета не может иметь окрестность второго или третьего типа: действительно, в этих случаях была бы вершина первого цвета, смежная с тремя вершинами нулевого цвета, а потому ац < 3. Значит, раскраска такова, что любая вершина нулевого цвета имеет окрестность первого типа. Тогда приходим к противоречию с параметрами, подбирая цвета для вершин u и v:

11 0 1

11 0 0 1

11 0 1 uv

Таким образом, дистанционно регулярных раскрасок с данной матрицей параметров не существует.

[33-33].

Пуств раскраска такова, что имеется вершина нулевого цвета с окрестностью третьего типа. Тогда приходим к противоречию с параметрами, подбирая цвета для вершин u, v іі w:

u 11 11

11 0 1 11

11 1 0 0 v

11 0 1 11

w 11 11

Значит, все вершины нулевого цвета имеют окрестности первого и второго типа. Пусть есть вершина цвета 0 с окрестностью второго типа. Восстанавливаем раскраску в соответсвии с параметрами и учитываем, что вершины нулевого цвета не могут иметь окрестность третьего типа. Получаем, что она периодична и однозначно продолжается на весь бесконечный граф:

19 19

08 17 06 06 17 08 17 17 08 19

08 17 15 02 11  0  0  15 06 17 19

08 15 02 11 1 0 1 04 06 17

08 15 04 02 11  0  1  13 04 17

08 17 15 04 13 02 02 13 04 17 19

08 17 06 15 15 06 17 08 08 19

19 19

Соответствующий вершинам нулевого цвета полностью регулярный код есть

По = J {Д^т+і(_ж^-2_ур : m,n Е Z}.

[42 -... ] .

Матрицы [42-60], [42-51], [42-42] и [42-33], с точностью до центральной симметрии, были рассмотрены ранее. Для матрицы параметров [42-15] дистанционно регулярная раскраска не существует вследствие леммы 2. Осталось рассмотреть матрицу параметров [42-24].

[42-24].

Окрестность произвольной вершины цвета 0 может быть одного из следующих трех типов:

101 00

В случаях, когда окрестность вершины нулевого цвета второго или третьего типа, имеется смежная с ней вершина первого цвета, у которой более двух соседей цвета 0, что противоречит параметрам раскраски. Значит, любая вершина нулевого цвета имеет окрестность второго типа. Поскольку матрица параметров центрально симметрична, то аналогичное утверждение верно и для окрестностей вершин первого цвета. Нетрудно построить единственную раскраску, удовлетворяющую этим условиям:

08 06 06 06 08

19 17 15 13 13 15 17 19

18 16 14 12 12 12 14 16 18

07 05 03 01 0 0 01 03 05 07

07 05 03 01 0 0 0 01 03 05 07

18 16 14 12 1 1 12 14 16 18

19 17 15 13 13 13 15 17 19

08 06 04 04 06 08

09 07 07 07 09

Она редуцируема, и формула для полностью регулярного кода V0 очевидна.

[51-...].

Вследствие леммы 2, может существовать только дистанционно регулярная раскраска с матрицей параметров [51-06], но этот случай был рассмотрен ранее.

• 6.    Заключительные замечания

• 7.    Приложение. Список полностью регулярных кодов в треугольной решетке

Доказательство теоремы закончено: сначала в разделе 2 были рассмотрены все дистанционно регулярные раскраски в четыре и более цветов, и они все оказались редуцируемыми; в разделах 4 и 5 были рассмотрены все возможные матрицы параметров порядка 2 и 3.

Для матрицы параметров [06-15] существует единственная с точностью до эквивалентности дистанционно регулярная раскраска, дающая в качестве вершин нулевого цвета совершенный код. Для матрицы параметров [15-24] также существует единственная с точностью до эквивалентности дистанционно регулярная раскраска, вершины нулевого цвета которой образуют объединение двух смежных классов по совершенному коду. Для матрицы параметров [24-33] существует уже две неэквивалентных дистанционно регулярных раскраски, вершины нулевого цвета каждой из которых образуют объединение трех смежных классов по совершенному коду.

Результаты данной работы были частично представлены на международной конференции «Мальцевские чтения» [11].

Полностью регулярные коды упорядочены по матрицам параметров дистанционно регулярных раскрасок, цветом которых они являются. Приведено число цветов, матрица параметров, фрагмент раскраски и конструкции для двух соответствующих полностью регулярных кодов. В случае раскраски в два цвета формулой описан только один из кодов.

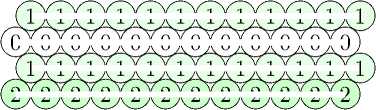
к = 3,4,5,... [24-222-... -222-42] П0 = {хту2(к-1> : т, п Е Z} Vk-1 = {у- yW-y+i^-1 : т,п Е Z}

000000000000 111111111111 222222222222

к = 3,4,5,...

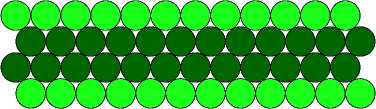
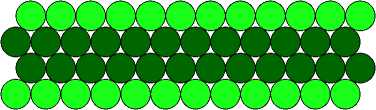
[24-222-... -222-24]

ТО = {$^my^(2k-1)” : m,n G Z}

V_k-1 = {ж^т _y^(2k->+^k-1 : m,_n G Z} ^J {_x^m_y^(2k-1)”+^k : m,n G Z}

к = 3, 4, 5,...

[42-222- . . . -222-24]

ТО = {x^my^2kn : m,n G Z} J

{_хту2Ы+1 : m,_ra G Z}

Tk—i = {x^my^2kn+k : m,n G Z} J {^^m_y^2kn+^k+1 : m, n G Z}

к = 3

[06-123-24]

То = {_ж^4ту^4п : m, n G Z}

V2 = {^V : n G Z} J {У2У¹ : n G Z} J {22ж” : n G Z}

к = 3

[06-123-33]

ТО = {(ж³2^-1)^т(у³ж^-1)” : m,n G Z}

V2 = {^² v , $^-2 v : v G To} J

{y² v , y^-2 v : v G Vo} ^J

{z² v , 2^-2 v : v G Vo}

к = 3

[06-132-60]

ТО = {ж3ту3п : m, n G Z}

V₂ = {(ж^-1у)ж^3ту^3п : m, n G Z} J {(xy^-1')x^3my³ⁿ : m,n G Z}

к = 3 [06-141-60] ТО = {(ж2у-1)ту4и : т,п Е Z} Т2 = {(ж2у)(ж2у-1)ту4п : т, п Е Z} 10 21 11 10 11 11 01 11 12 01 1112111011 1101112111 2111011121 1112111011 1011121110 2111011121 1121110111 1011121110 1110111211 1121110111 11 1011111101 к = 2 10 1111110111 [06-15] 11 1110111111 ТО = {(ж-1у2)т(г-1ж2)п : т, п Е Z} 11 01 1011111101 1111101111 11 1110111111 11 0111111011 01 1111101111 01 0101010101 11 1111111111 к = 2 01 0101010101 [06-24] 11 1111111111 То = {ж2т+е-/Д' : т,п Е Z}, 10 1010101010 Е^ Е {0,1},п Е Z 11 1111111111 10 1010101010 11 1111111111 01 0101010101 11 1111111111 10 1010101010 к = 2 10 1101101101 [06-33] 01 1011011011 То = {ж3т(ж—1у)п : т,п Е Z} 10 01 1101101101 1011011011 10 1101101101 01 1011011011 к = 2

[15-24]

ТО = {(ж^-1у²)^т(г^-1ж²)^п : т, п Е Z} U {х(х^-1'у²у^т(2Г¹х²у^г : т, п Е Z}

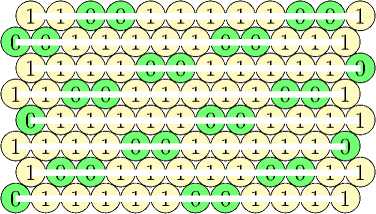
к = 2 [15-33] Ио = {x4m+1 y4n :m,n Е Z} U {x4m+2y4n : m, n Е Z} U {x4my4n+1 : m, n Е z } u {x4m-1y4n+3 : m,n Е Z} U {x^m+e"y4n+2 :m,n Е Z}, en Е {0,1},n Е Z	101110111011 010101010101 111011101110 001100110011 111011101110 101010101010 101110111011 110011001100 101110111011 010101010101 111011101110 001100110011 111011101110 101010101010 101110111011
к = 2 [24-24] P0 = {x3my3n : m, n Е Z} U {x3m-1y3n : m, n Е Z} U {x3my3n+1 : m, n Е Z}	011011011011 001001001001 111111111111 110110110110 100100100100 111111111111 011011011011 001001001001 111111111111 110110110110
к = 2 [24-24] P0 = {xmy3n : m, n Е Z}	111111111111 000000000000 111111111111 111111111111 000000000000 111111111111 111111111111
	000000000000 111111111111

к = 2 [24-42] V = Ц=0 R^, Ro = {e,x,z 1}, Rj = { v : d(Ro, v ) = j }	5X0X5®®®©©)©®©® ш©©©©©©©©©©©5 X©©©©©©©©©©©© ©©©©©©©©©©©©x Ху©©©©©©©©©©© ©©©©©©©©©©©©у Х0)©©©©Х0Х0Х0Х5©ф© ©©©©©©©©©©©ХХ j@x@@x@@)C0Xix@C0^^
к = 2 [24-42] Vo = {жту2п+ет : m,n e Z}, Em G{0,і},п G Z	©©©©©©©©©©©©г @©©©!0)©©©©©©© ©©©©©©©©©©©©x ©©©©©@5©©©©© ©©©©©©©©©©©x© (0X0X5©©©©©©©©© ©©©©©©©©©©©©L ©©©©©©©©©©©© ©©©©©©©©©©©Xy X©©©©©©©©©©©)
к = 2 [33-33] Vo = U3=o{^m+4^-2yF : m,n G Z}	©©©©©©©©©©©©) 55©©©©©©©©©©© ©©©©©©©©©©©©> @©©®©©©©©©©© ©©©©©©©©©©©©: Xx©©©©©©©©©©© @(0ХіХіХіХіХ0Х0Х0Х0Хі^^
к = 2 [42-24] Vo = {жту4п : m,n G Z} U {xmy4n+1 : m, n G Z}	(0X0X0X03X0X0X0X0X0X0X0) ©©©©XX©©©©©©©) д5©©©©©Х5©©©©©) ©©©©©©©©©©©©) 50X0X0X0X0X0X0X0X0X0X0X0) ©©XD©Xx©©©(©5©X3 @©(0X0X0X0)C0X0X0X0X0X0X