Полностью волоконный вентиль SWAP-CNOT для оптических вихрей
Автор: Баршак Елена Владимировна, Лапин Борис Петрович, Викулин Дмитрий Вячеславович, Алиева Селиме Сейрановна, Алексеев Константин Николаевич, Яворский Максим Александрович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 6 т.45, 2021 года.
Бесплатный доступ
В данной работе исследовано распространение оптических вихрей в системе оптических волокон, состоящей из последовательно расположенных мультигеликоидального и скрученного анизотропного волокон. Показано, что в определенных резонансных режимах оптических волокон такая система позволяет осуществлять контролируемое изменение знака топологического заряда и циркулярной поляризации входного оптического вихря. Кроме того, установлены параметры мультигеликоидального и анизотропного волокон, при которых исследуемая система реализует логическую операцию, которая соответствует последовательному применению базовых двухкубитовых вентилей SWAP и CNOT над состояниями циркулярно поляризованных оптических вихрей.
Оптические вихри, орбитальный угловой момент, логические элементы, анизотропные оптические волокна, двулучепреломление, волоконная оптика
Короткий адрес: https://sciup.org/140290283
IDR: 140290283 | DOI: 10.18287/2412-6179-CO-938
Текст научной статьи Полностью волоконный вентиль SWAP-CNOT для оптических вихрей
Многосторонние теоретические и экспериментальные исследования показали, что использование оптических вихрей (ОВ) [1] открывает новые практические возможности в различных областях: от генной инженерии [2, 3] и микроскопии [4] до оптики атмосферы и астрофизики [5–7]. Следует выделить высокий потенциал применения ОВ в инфокоммуникаци-онной сфере [8– 10], базирующийся на возможности кодировать информацию в значениях орбитального углового момента (ОУМ) ОВ [1, 11 – 13]. Технологии, основанные на использовании орбитальных степеней свободы оптического излучения, имеют существенные преимущества в передаче данных над традиционными способами кодирования информации. Техника ОУМ-мультиплексирования, в которой реализуется передача информации на ортогональных состояниях ОВ с разными значениями ОУМ, позволяет значительно увеличить пропускную способность канала связи [8, 14– 17]. Кроме того, передача информации в значениях ОУМ ОВ обеспечивает принципиально новый уровень защиты данных [18].
Практические возможности переносящих ОУМ ОВ проявляются также в области построения квантовых систем, оперирующих с квантовыми элементарными ячейками – кубитами. Классические состояния фотонов с ОУМ находят применение в моделировании квантовых алгоритмов для квантовых компьютеров. Такой подход позволяет проверить и отладить работу алгоритмов квантовых вычислений, избежав дорогостоящих экспериментов над квантовыми си-
стемами. Одной из основных задач данного направления исследований является проблема реализации логических вентилей (гейтов), выполняющих базовые логические операции над состояниями ОВ с разными значениями ОУМ. Ранее было установлено, что успешное решение подобных задач может осуществляться с помощью определенных типов оптических волокон, позволяющих передавать ОВ на расстояние, осуществлять контроль и управление их параметрами [19–27]. Так, на основе акустически-управляемых [19, 20] и мультигеликоидальных оптических волокон (МВ) [21] предложены способы реализации двуку-битного гейта CNOT (управляемое НЕ), в котором линейная поляризация оптического пучка является управляющим кубитом, а топологический заряд – управляемым. Недавние исследования [22] позволили установить возможность функционирования МВ как трехкубитного логического вентиля Тоффоли, в котором управляющими кубитами служат радиальное число и состояние поляризации, а управляемым – топологический заряд входящего ОВ. Также было показано, что гейт Тоффоли реализуется в скрученном анизотропном волокне (САВ), при этом циркулярная поляризация ОВ становится управляемым, а топологический заряд – управляющим кубитом. Отметим, что оптоволоконный подход к реализации логических элементов обладает рядом практических преимуществ, заключающихся в удобстве сопряжения чисто волоконных элементов друг с другом, включающем уменьшение потери мощности излучения и вносимых шумовых помех, а также в увеличении эффективности преобразования оптического пучка в волокне.
Упомянутые исследования обнаруживают перспективы практического применения ОВ, передаваемых в определенных типах оптических волокон, в области квантовых вычислений. Очевидно, что соблюдение принципов минимизации при построении логических устройств требует расширения набора операций над состояниями фотонов и оптимизации логических схем в оптических волокнах. В данной работе предлагается способ реализации волоконной схемы, состоящей из МВ и САВ (М-А), которая осуществляет сразу две двухкубитные операции SWAP и CNOT над оптическими вихрями.
1. Резонансные модовые режимы в системе волокон М-А
Модель САВ (рис. 1 а ) описывается следующим тензором диэлектрической проницаемости [23]:
Б а ( Г , ф , z ) = Б ( Г ) 1 + Б Ан ( Г , ф , z ) + Б КМН ( Г , ф ) . (1)
Первое слагаемое в выражении (1) б ( r ) = Б с (1 - 2 A f ( r )) описывает диэлектрическую проницаемость идеального волокна (ИВ), A = ( e c - Б об ) / 2 б с - высота профиля диэлектрической проницаемости, Б c и Б об - значения диэлектрической проницаемости в сердцевине и оболочке волокна соответственно. В данной работе рассматриваются слабонаправляющие оптические волокна, для которых A << 1, что обуславливает параксиальный характер распространения оптических мод. Функция f ( r ) определяет распределение показателя преломления среды и для рассматриваемых оптических волокон со ступенчатым профилем показателя преломления имеет вид f ( r ) = © ( R -1), где © - функция Хевисайда, R = r / r 0 , r 0 – радиус сердцевины волокна. Используется цилиндрическая система координат ( r , ф , z ), ось z которой совпадает с осью волокна.
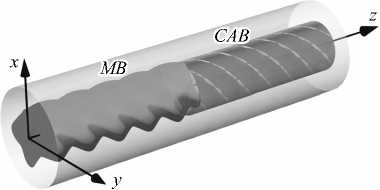
Рис. 1. Модель системы оптических волокон М-А: МВ с параметром симметрии τ = 4 и САВ
Второе слагаемое в выражении (1) описывает влияние линейной анизотропии материала волокна:
|
г cos 2 9 |
sin 2 9 |
0" |
|
|
Б Ан ( z ) 5б Ан |
sin 2 9 |
- cos 2 9 |
0 |
|
ч 0 |
0 |
-1y |
где 5б дн = (1/2) ( б x - Б у ), 9 = qz = (2 п / H) z - угол поворота оси анизотропии, H – шаг скрутки волокна.
Третье слагаемое в (1) характеризует влияние крутильных механических напряжений (КМН):
Модели МВ (рис. 1 б ) соответствует тензор диэлектрической проницаемости следующего вида [21, 23]:
Б м ( r , Ф , z ) = Б ( r ) 1 + Б ф ( r , ф , z ) 1 + Б кмн ( r , ф ) . (4)
Здесь второе слагаемое описывает влияние анизотропии формы волокна на диэлектрическую проницаемость:
Б ф ( r , ф , z ) = - 2 8Б ф rfr ( r ) cos т ( ф- qz ) , (5)
где т =2,4... - параметр симметрии поперечного сечения, 5б ф = Б с 5А , 5 << 1 - параметр деформации поперечного сечения, штрих означает производную по r .
В предыдущих исследованиях [21, 24] было установлено, что модами высшего порядка САВ и МВ при условии 5б Ан , 5б ф ^ 2 k - 1 |3 q - | 1 | A / kr 0 2 | оказываются циркулярно-поляризованные ОВ с 1 1 1 > 2:
11,^|), |1,^|}, |1,-^|), |-1,-^|\ (6)
где
[ rF. п'F,| (r)] e ™M , a,У = —?=e'<фF< (r) 1,iст,У—
V2 e r
I = ± 2, ± 3... - топологический заряд ОВ, a = ± 1 описывает знак циркулярной поляризации, Т означает транспонирование. Радиальная функция F ^ ( r ) выражается через функции Бесселя J\ t\ ( r ) и K \t\ ( r ) в сердцевине и оболочке волокна соответственно [28]. Радиальное число здесь опущено для упрощения записи.
Отметим, что высшими модами с 1 1 1 = 1 рассматриваемых волокон оказываются не четыре циркулярно-поляризованных вихря, как в выражении (6), а два ОВ |1,1 ) , |-1,-1 ) , а также ТЕ- и ТМ-мода [23]. Поскольку в данной работе исследуется возможность осуществления логических операций над ОВ, мы ограничиваемся случаем 1 1 1 > 2, в котором представлены четыре независимых ОВ.
Постоянные распространения мод (6) имеют вид:
ра/ =рм +5в СО + ( a + fc ) aq , (7)
где в Z| - известная скалярная постоянная распространения [28], второе слагаемое
5Р СО = A ( F ' ( 1 ) -С £ )/2рм r o2 ( R ) Q z| , (8)
где f«
. 0 RF\fc| (R) dR, обусловлено оптическим спин-орбитальным взаимодействием (СОВ), а третье – влиянием скрутки, включая КМН, где a = 1 – εc |p44| /2.
Принципиально отметить, что зависимость постоянных распространения (7) от параметра скрутки q определяет степень влияния анизотропии (материала в случае САВ или формы в случае МВ) на структуру мод волокна. Так, поля (6) остаются модами САВ и МВ, пока спектр (7) является невырожденным. Однако при определенных резонансных значениях шага скрутки имеет место двукратное вырождение постоянных распространения (7) (рис. 2).
\V .'10 . м-'
1,46289
1,46288
1,46287
1,46286
1,46285
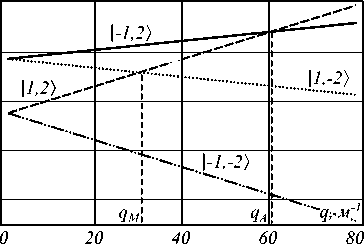
Рис. 2. Постоянные распространения (7) |ℓ| = 2 мод (6) как функция параметра скрутки q. Точки пересечения кривых – резонансные точки, вблизи которых влияние анизотропии материала (в точке q A ) или формы (в точке q m ) волокна приводит к новой структуре мод. Параметры волокна: волноводный параметр V = 6,58, ∆ = 0,01, r 0 = 5λ He-Ne , p 44 = 0,075
В таких точках резонанса степень влияния анизотропии материала или формы волокна резко возрастает и приводит к формированию новой структуры мод. Так, в САВ моды в резонансной точке q а = A | , | г 2 (2 а в^ О м) - 1 имеют вид [22]:
| ^(А)^ = cos а |1, |,|у + sin а|- 1, |,|/
| V 2А / = sin а 1 1, |,|- cos а | - 1, |,| , (9)
I ^3А)) = |1, -|,|у |^4А/ = |-1, -|,|у где cos (2α) = aεA/ ГА, εA= q – qA, ΓA=(aεA)2 +Ω2A
Q a = к 2 3s Ah /2 в | < | , к — волновое число.
Постоянные распространения мод (9):
в (М) =в 1,| , ( q м ) - а S м ±Г м , в 3М4) = РМ +8в“| , + ( - 1 ± И) aq ,
где cos (2 ц ) = а | , | S m / Г м , S m = q- q M ,
Г м = ( а |—I S m ) + ^ М ,
Q m = - к 2 s c аз/ 2вм Г о2 ( R ) JJ R^ , 2 ( R ) dR .
Выражения для мод (9) и (12) справедливы при условии 3s Ah, 3s << 4 | , | A ( кг 0) -2, когда влияние анизотропии (материала или формы) приводит к гибридизации только тех ОВ, чьи уровни пересекаются в резонансной точке.
Используя приведенные выражения (9)–(12), рассмотрим распространение циркулярно поляризованных ОВ | о , , ) в системе оптических волокон, состоящей из последовательно соединенного МВ и САВ, находящихся в резонансных режимах.
-
2. Трансформация оптических вихрей в системе оптических волокон М-А
Пусть на входе первого в системе МВ вблизи резонансной точки q M возбуждается ОВ:
| V ( z = 0 )) = |а, , . (13)
Это приводит к возникновению в МВ поля, представленного суперпозицией собственных мод МВ (11):
Ψ( М ) ( z ) = ∑ b i Ψ i ( М ) exp( i β i ( М ) z ). (14)
Коэффициенты разложения в (14) легко найти из граничных условий к уравнениям Максвелла, которые в параксиальном приближении сводятся к непрерывности полей на входном торце волокна:
| G,, = £ bi |v (М) у i
В табл. 1 приведены коэффициенты b i для случаев возбуждения на входе МВ право- и левоциркулярно поляризованных ОВ с топологическими зарядами ± | , |.
в (А) =в 1,| , ( q a ) - a S a ±Г а , в 3А4) = вМ + Зв СО ±|, + ( ± 1 - И ) aq .
Моды МВ и их постоянные распространения вблизи резонансного значения параметра скрутки q М = A г 0 2 (2 а в , О , )' представлены следующими выражениями [21]:
Табл. 1. Коэффициенты разложения (14) ОВ для МВ
|
ОВ на входе МВ |
b 1 |
b 2 |
b 3 |
b 4 |
|
11,| . | ) |
VV2 |
-1/42 |
0 |
0 |
|
|-1,Н ) |
0 |
0 |
1 |
0 |
|
11,-Н ) |
1/42 |
-1/42 |
0 |
0 |
|
|-1,-Н ) |
0 |
0 |
0 |
1 |
| ^ 1(М)^ = cos ц |1, |,|^ + sin ц |1, - |,| У
| V 2М)^ = sin ц |1, |.ф - cos ц |1, -|,| У (11)
I^ 3М)) = |- 1, |-| у Ц 4М)) = |- 1, - 1-| у
В следующем волокне рассматриваемой системы – САВ – поле записывается в виде суперпозиции мод (9):
Ψ( А ) ( z ) = ∑ с i Ψ i ( А ) exp( i β( i А ) z ).
Чтобы найти связь коэффициентов разложения (16) c i и (14) b i , используем условие непрерывности поля на границе МВ и САВ при z = z M ( z M – длина МВ):
£ b ^ / М))exp( i в( М ) z М ) = £ C i |^(А)) exp( e А z м ). (17)
Коэффициенты c i получаем в виде:
c1 = cos a exp( - i в (А) z М ) [ b cos ц exp( i в (М) z М ) + b 2 sin ц exp( i в 2М) z М ) + b 3 tg a exp( i в 3М) z М ) ] , c 2 = sin a exp( - i в 2А) z М ) [ b cos ц exp( i в (М) z М ) + b 2 sin ц exp( i в 2М) z М ) - b 3 ctg a exp( i в 3М) z М ) J , (18)
c з = exp( - i в 3А) z м ) [ b i sin ц exp( i в (М) z м ) - b 2 cos ц exp( i в 2М) z м ) ] , c 4 = b 4 exp( i ( в 4М) -в 4А) ) z м ).
Используя выражения для мод (9), запишем поле (16) в следующем виде:
|^<А) ( z a )) = d i,| < I1, ki)
+ d - i,|<|
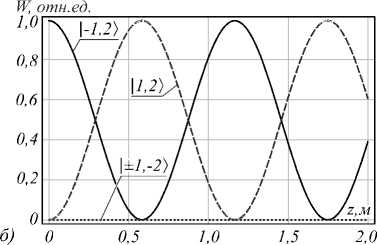
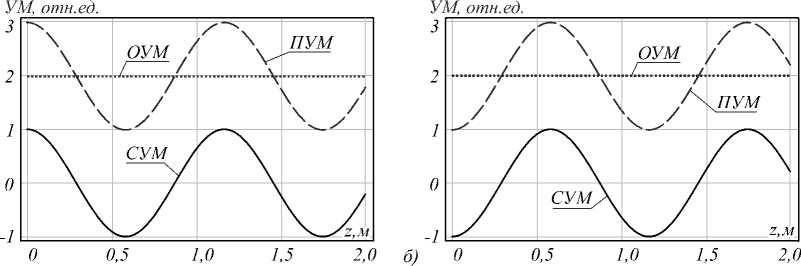
I-1’l +d 1,-1 <1|1- И)+d-1,-1 <11-1, - И), где d 1,|< = c1 cos a exp(iв(А)zA) + c2 sin a exp(iв2А)zA), d_1,|< = c1 sin a exp(iв(А)zA) - c2 cos a exp(iв(2А)zA), d 1,-|<| = c3 exp(iв3А)zA), d-1,-1 < = c4 exp^4"’zA), zA - длина САВ. Коэффициенты da,t позволяют определить энергию Wз,£, сосредоточенную в соответствующем парциальном ОВ поля (19): Wa,t = da,<| 2. (20) В качестве примера рассмотрим случай, когда | < | = 2. На рис. 3а,б продемонстрирована зависимость величины энергии парциальных ОВ Wт, ± 2 на выходе системы М-А в зависимости от длины САВ. Параметры МВ и САВ в данном примере заданы в рамках диапазонов типичных значений оптических волокон. Величина скрутки такова, что оба волокна системы М-А находятся в резонансных режимах, в которых реализуется особая модовая структура: (9) в САВ и (11) в МВ при параметрах скрутки qA=60,5 м–1 и qM = 30,2 м–1 [22] соответственно. Рис. 3а соответствует случаю, когда на входе системы М-А возбуждается правоциркулярно поляризованный ОВ с отрицательным знаком топологического заряда |1,-2). Длина МВ фиксирована и выбрана равной zM = 0,25 м, что обусловлено особенностью распределения энер- гии в МВ на этой длине [22]. Действительно, оказывается, что благодаря связи правоциркулярно поляризованных ОВ с противоположным знаком топологического заряда в резонансных модах МВ (11) можно выбрать такие параметры волокна, что на некоторой длине МВ (zM = 0,25 м в рассматриваемом примере) энергия ОВ |1,-2) полностью аккумулируется в ОВ |1,2), и наоборот. Таким образом, если на вход системы М-А подается ОВ |1,-2), при указанной длине МВ на входе САВ оказывается ОВ |1,2) (см. рис 3а при zA =0). Аналогично из структуры мод САВ (9) видно, что ОВ |1,2) в САВ может быть преобразован в ортогональный ОВ с тем же знаком топологического заряда |-1,2). На рис. 3а показано, что на длине САВ zA=0,6 м вся энергия сконцентрирована в ОВ |-1,2). Таким образом, действие системы М-А сводится к преобразованию поля |1,-2) в ОВ с противоположным знаком циркулярной поляризации и топологического заряда: 11, -2) ^1-1,2). (21) Соответствующие величины ОУМ, спинового (СУМ) и полного углового момента (ПУМ) поля на выходе системы М-А представлены на рис. 4а. Отметим, что инверсия ОУМ входного ОВ в системе М-А происходит вне зависимости от длины САВ. На рис. 3б и 4б показано распределение энергии и величины угловых моментов поля (19) при возбуждении системы ОВ |-1,2). Такой ОВ является модой МВ, поэтому не преобразуется в первом волокне системы. При этом в САВ на длине zA =0,6 м входной ОВ полностью трансформируется в ОВ с ортогональной поляризацией: |-1,2) ^ |1,2>. (22) Рис. 3. Распределение энергии поля (19) по парциальным ОВ в системе М-А в зависимости от длины САВ, если на входе системы возбуждается ОВ: \1,-2) (а), 1—1,2) (б). Параметры волокон в системе М-А: волноводный параметр V=6,58, Л=0,01, ro=5XHe-Ne, p44=0,0 75, 5=10-4, qM=3 0,2м-1, zm=0,25м, 8eah=8-№7, qA=60,5м-1 а) Рис. 4. ОУМ, СУМ и ПУМ поля (19) в зависимости от длины САВ, если на входе системы М-А возбуждается ОВ: \1,-2>(а), \-1,2>(б). Параметры волокон в системе М-А: волноводный параметр V=6,58, Л=0,01, ro=5XHe-Ne, p44=0,0 75, 3=1^4, qM=3 0,2м-1, zm=0,25м, 5sah=8-10-7, qA=60,5м-1 Кроме того, установлено, что энергия входящего ОВ |1,2>в рассматриваемой системе волокон полностью переходит в энергию ОВ с противоположным знаком топологического заряда: 11,2>^ 1 —2. (23) Такая трансформация ОВ происходит в МВ на длине zM = 0,25 м, так что на входе САВ в этом случае оказывается его собственная мода - ОВ |1,-2>, поэтому конверсия (23) не зависит от длины САВ. Отметим, что при отклонении величины шага скрутки от резонансного значения энергетическая эффективность преобразований (21 –23) снижается. В рассматриваемом примере в МВ энергетическая эффективность снижается на 5 %, если шаг скрутки отклоняется на 5 мм, а в САВ – при отклонении шага скрутки на 1 мм. При этом отклонение от оптимальной длины МВ на 1 см снижает эффективность трансформации ОВ на 0,4%. Отклонение величины длины САВ от оптимальной в рамках 1 см не оказывает заметного влияния (см. рис. 3а,б) – эффективность преобразования снижается менее чем на 0,1 %. Наконец, ОВ |-1,-2>, являясь собственной модой как МВ, так и САВ, не претерпевает изменений в системе, состоящей из данных оптических волокон: |-1, -2) ^|-1, -2). (24)
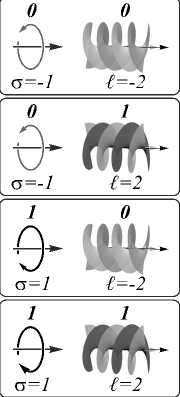
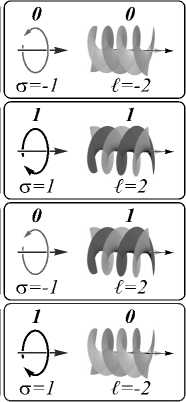
3. Схема квантовых гейтов SWAP→CNOT Используя установленные преобразования ОВ (21 – 24), покажем, что система волокон М-А может быть использована для реализации логической схемы для ОВ, эквивалентной последовательному выполнению двух фундаментальных квантовых логических вентилей SWAP и CNOT. Логические элементы SWAP и CNOT имеют два входа и два выхода и могут быть описаны соответствующими таблицами истинности (табл. 2), где A, B обозначают сигнал на входе, A', B' – на выходе логического элемента. Таблица истинности логической схемы, состоящей из вентилей SWAP и CNOT, записывается в форме, приведенной в табл. 3. Табл. 2. Таблицы истинности SWAP и CNOT гейтов SWAP CNOT A B A’ B’ A B A’ B’ 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 1 1 1 1 1 1 1 0 Табл. 3. Таблица истинности схемы последовательного выполнения SWAP и CNOT A B A’ B’ 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 В качестве входного кубита A будем рассматривать состояние поляризации ОВ на входе системы оптических волокон М-А, а в качестве кубита B – его топологический заряд. Пусть а =-1 соответствует A = 0, а = 1 - A = 1, / = -2 - B = 0, / = 2 - B = 1. Подавая на вход системы М-А с установленными длинами МВ (zм = 0,25м) и САВ (za = 0,6м) ОВ |-1,-2>, |-1, 2), |1,-2), |1, 2>, на выходе системы получим ОВ согласно выражениям (21 – 24). На рис. 5 показаны состояние поляризации и топологического заряда ОВ на входе и выходе М-А. Сравнивая полученный результат с табл. 3, можно заключить, что система М-А с установленными параметрами применима для реализации операции последовательного выполнения двух квантовых гейтов SWAP и CNOT. Анализ показывает (см. рис. 3), что точный подбор параметров оптических волокон в системе М-А позволяет добиться высокой энергетической эффективности преобразования ОВ (до 100%), требуемой для корректного выполнения предлагаемой логической схемы SWAP и CNOT гейтов. Может показаться, что рассмотренная схема последовательного выполнения двух гейтов SWAP и CNOT сводится к реализации гейта SWAP в первом МВ системы, а гейта CNOT – во втором САВ. Однако это не является истиной. Более того, особенностью данной системы оказывается тот факт, что если придерживаться выбранного выше правила соответствия поляризации ОВ кубиту A, а его топологического заряда – кубиту B, то оказывается, что в МВ реализует- ся гейт CNOT [21], а не SWAP, как можно было бы предположить. При этих условиях в САВ не очевидна возможность реализации какой-либо базовой логической операции. Вход Выход Рис. 5. ОВ на входе и выходе в системе М-А: реализация логической схемы двух квантовых гейтов SWAP и CNOT. Параметры волокон в системе М-А: V=6,58, ∆=0,01, r0=5λHe-Ne , p44=0,075, δ=10–4, qM=30,2 м–1, zM=0,25 м, δεAн=8⋅10–7, qA=60,5 м–1 Заключение В данной работе исследовано распространение ОВ, обладающих целым на фотон ОУМ, в системе последовательно соединенных оптических волокон: МВ и САВ. Показано, что при определенных резонансных режимах оптических волокон такая система позволяет осуществлять управление знаком топологического заряда и циркулярной поляризации выходного поля посредством изменения знака ОУМ и СУМ входного оптического вихря. На основе этого эффекта предложена полностью волоконная реализация логической схемы, состоящей из двух квантовых гейтов SWAP и CNOT. Численно установлены параметры МВ и САВ, позволяющие обеспечить эффективную реализацию логической схемы SWAP и CNOT гейта в системе М-А. Работа выполнена при поддержке Совета по грантам Президента Российской Федерации, грант № МК-329.2020.2 (исследование управления угловым моментом оптических вихрей), и РФФИ, проект № 2047-910001 (численный подбор параметров волокон для реализации вентилей SWAP и CNOT).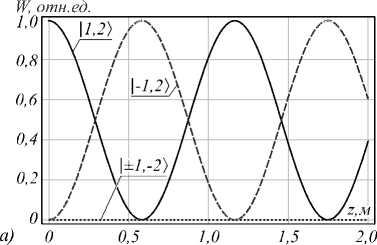
Список литературы Полностью волоконный вентиль SWAP-CNOT для оптических вихрей
- Shen, Y. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities / Y. Shen, X. Wang, X. Zhenwei, C. Min, X. Fu, Q. Liu, M. Gong, X. Yuan // Light: Science & Applications. - 2019. - Vol. S. - 90. - DOI: 10.1038/s41377-019-0194-2.
- Friese, M.E.J. Optical alignment and spinning of laser-trapped microscopic particles / M.E.J. Friese, T.A. Nieminen, N.R. Heckenberg, H. Rubinsztein-Dunlop // Nature. - 1998. - Vol. 394. - P. 348-350.
- Garces-Chavez, V. Transfer of orbital angular momentum to an optically trapped low-index particle / V. Garces-Chavez, K. Volke-Sepulveda, S. Chavez-Cerda, W. Sibbett, K. Dholakia // Physical Review A. - 2002. - Vol. 66. -063402.
- Spektor, B. Singular beam microscopy / B. Spektor, A. Normatov, J. Shamir // Applied Optics. - 2008. -Vol. 47. - P. A78-A87.
- Foo, G. Optical vortex coronograph / G. Foo, D.M. Palacios, G.A. Shwartzlander, Jr. // Optics Letters. -2005. - Vol. 30. - P. 3308-3310.
- Swartzlander, G.A., Jr. Peering into darkness with a vortex spatial filter / G.A. Swartzlander, Jr. // Optics Letters. -2001. - Vol. 26. - P. 497-499.
- Soifer, V.A. Vortex beams in turbulent media: review / V.A. Soifer, O. Korotkova, S.N. Khonina, E.A. Shchepakina // Computer Optics. - 2016. - Vol. 40(5).- P. 605-624. - DOI: 10.18287/2412-6179-2016-40-5-605624.
- Bozinovic, N. Terabit-scale orbital angular momentum mode division multiplexing in fibers / N. Bozinovic, Y. Yue, Y. Ren, M. Tur, P. Kristensen, H. Huang, A.E. Willner, S. Ramachandran // Science. - 2013. -Vol. 340. - 1545.
- Qiao, W. Approach to multiplexing fiber communication with cylindrical vector beams / W. Qiao, T. Lei, Z. Wu, S. Gao, Z. Li, X. Yuan // Optics Letters. - 2017. - Vol. 42. - P. 2579-2582.
- Карпеев, С.В. Передача через атмосферу высокоскоростного сигнала формата 1000BASE-SX/LX вихревыми пучками ближнего ИК-диапазона при помощи модифицированных SFP-трансиверов DEM-310GT / С.В. Карпеев, В.В. Подлипнов, Н.А. Ивлиев, С.Н. Хонина // Компьютерная оптика. - 2020. - Т. 44, № 4. - С. 578-581. - DOI: 10.18287/2412-6179-CO-772.
- Yao, M. Orbital angular momentum: origins, behavior and applications / M. Yao, M.J. Padgett // Advances in Optics and Photonics. - 2011. - Vol. 3. - P. 161-204.
- Willner, E. Optical communications using orbital angular momentum beams / E. Willner, H. Huang, Y. Yan [et al.] // Advances in Optics and Photonics. - 2015. - Vol. 7. -P. 66-106.
- Padgett, M.J. Orbital angular momentum 25 years on / M.J. Padgett // Optics Express. - 2017. - Vol. 25, Issue 10. - P. 11265-11274. - DOI: 10.1364/OE.25.011265.
- Essiambre, R. Capacity trends and limits of optical communication networks / R. Essiambre, R. Tkach // Proceedings of the IEEE. - 2012. - Vol. 100. - P. 1035-1055.
- Wang, J. Terabit free-space data transmission employing orbital angular momentum multiplexing / J. Wang, J.Y. Yang, I.M. Fazal, N. Ahmed, Y. Yan, H. Huang, Y. Ren, Y. Yue, S. Dolinar, M. Tur, A.E. Willner // Nature Photonics. - 2012. - Vol. 6. - P. 488-496.
- Wang, F.-X. Scalable orbital-angular-momentum sorting without destroying photon states / F.-X. Wang, W. Chen, Z.-Q. Yin, S. Wang, G.-C. Guo, Z.-F. Han // Physical Review A. - 2016. - Vol. 94. - 033847.
- Dudley, A. All-digital wavefront sensing for structured light beams / A. Dudley, G. Milione, P.R. Alfano, A. Forbes // Optics Express. - 2014. - Vol. 22. - P. 14031-14040.
- Franke-Arnold, S. Uncertainty principle for angular position and angular momentum / S. Franke-Arnold, S. Barnett, E. Yao, J. Leach, J. Courtial, M. Padgett // New Journal of Physics. - 2004. - Vol. 6. - 103.
- Yavorsky, M.A. Polarization-dependent orbital angular momentum flipping in fibers with acousto-optic interaction / M.A. Yavorsky, D.V. Vikulin, E.V. Barshak, B.P. Lapin, C.N. Alexeyev // Journal of Physics: Conference Series. -2019. - Vol. 1368. - 022067. - DOI: 10.1088/17426596/1368/2/022067.
- Yavorsky, M.A. All-fiber polarization-dependent optical-vortex-controlling via acousto-optic interaction / M.A. Yavorsky, D.V. Vikulin, E.V. Barshak, B.P. Lapin, C.N. Alexeyev // Days on Diffraction (DD). - 2019. -P. 238-243. - DOI: 10.1109/DD46733.2019.9016567.
- Yavorsky, M.A. Spin-dependent OAM flipping in multihel-ical optical fibres / M.A. Yavorsky, E.V. Barshak, D.V. Vikulin, C.N. Alexeyev // Journal of Optics. - 2018. -Vol. 20, Issue 11. - 115601. - DOI: 10.1088/2040-8986/aae3ff.
- Alexeyev, C. Toffoli gate in twisted anisotropic and multiheli-cal optical fibers / C. Alexeyev, E. Barshak, D.V. Vikulin, B. Lapin, M. Yavorsky // Days on Diffraction (DD). - 2020. -P. 7-12. - DOI: 10.1109/DD49902.2020.9274577.
- Barshak, E.V. Twisted anisotropic fibers for robust orbital-angular-momentum-based information transmission /E.V. Barshak, C.N. Alexeyev, B.P. Lapin, M.A. Yavorsky // Physical Review A. - 2015. - Vol. 91. - 033833. - DOI: 10.1103/PhysRevA.91.033833.
- Barshak, E.V. Robust higher-order optical vortices for information transmission in twisted anisotropic optical fibers / E.V. Barshak, D.V. Vikulin, B.P. Lapin, S.S. Alieva, C.N. Alexeyev, M.A. Yavorsky // Journal of Optics. - 2021. - Vol. 23, Issue 3. - 035603. - DOI: 10.1088/2040-8986/abda85.
- Alexeyev, C.N. Transformation of optical vortices in elliptical and anisotropic optical fibres / C.N. Alexeyev, A.V. Volyar, M.A. Yavorsky // Journal of Optics A: Pure and Applied Optics. - 2007. - Vol. 9, Issue 4. - 387. - DOI: 10.1088/1464-4258/9/4/013.
- Alexeyev, C.N. Multi-helix chiral fibre filters of higherorder optical vortices / C.N. Alexeyev, A.V. Volyar, M.A. Yavorsky // Journal of Optics A: Pure and Applied Optics. - 2007. - Vol. 9, Issue 5. - 537. - DOI: 10.1088/1464-4258/9/5/018.
- Alexeyev, C.N. Helical-core fiber analog of a quarter-wave plate for orbital angular momentum / C.N. Alexeyev, B.P. Lapin, A.V. Volyar, M.A. Yavorsky // Optics Letters. -2013. - Vol. 38, Issue 13. - P. 2277-2279. - DOI: 10.1364/OL.38.002277.
- Optical waveguide theory / A. Snyder, J.D. Love. - London: Chapman and Hall, 1983.


