Полные системы в задачах восстановления сигнала

ставляют раздел прикладных исследований под названием «PHASE RETRIEVAL» (возвращение, воспроизведение фазы).

Пионерской работой в этом направлении является работа [3], в которой была доказана теоретическая возможность точного восстановления сигнала (с точностью до унимодулярного множителя), если в качестве системы представления используются полные избыточные системы.

Дальнейшее развитие идет по двум направлениям:

• 1)    поиск таких систем «измерительных» векторов которые позволят восстановить произвольный сигнал по набору вещественных чисел

• 2)    обоснование возможности восстановления произвольного сигнала с большой вероятностью для относительно небольшого числа «случайно выбранных» измерительных векторов.

Второй подход близок теории сжатого зондирования.

Следующее определение конкретизирует свойство инъективности отображения

17^{|{17,^г)|},е/, которое является ключевым в описываемом круге вопросов.

Определение. Набор векторов<— = ; ■^■}'. = ■ в jx" (или )о") обеспечивает воспроизведение фазы (ВФ), если для любых          (или    ), таких, что для всех получается равенство         где         для

(и       для где — единичная окруж ность на комплексной плоскости).

Фреймом конечномерного пространства называется любая полная система векторов, состоящая из, возможно, линейно зависимых элементов. Полнота системы означает, что ее линейная оболочка равна [1, 2].

Фрейм в обеспечивает восстановление фазы тогда и только тогда, когда он обладает свойством альтернативной полноты.

Известия Самарского научного центра Российской академии наук, т.17, №2(5), 2015

Альтернативная полнота системы означает, что при произвольном выборе ^S С { 1_; _ , N ^} либо {Ф п ^} n _{е s} , либо {Ф п ^} n _е SC ^полны в

В частности, полный спарк, содержащий,

по крайней мере, ² M

^^^^^^^е

1 векторов, допускает

г у^ г уДО восстановление фазы. Если допускает восстановление фазы в , то N > 2M -1, никакое подмножество из 2M - 2 элементов не может обеспечить восстановление фазы.

Спарком системы называется мощность наименьшего линейно зависимого подмножества этой системы. Если спарк системы больше размерности пространства, то любое подмножество из M элементов линейно независимо, в этом случае систему называют полным спарком [7] .

В пространстве свойство альтернативной полноты является лишь необходимым условием инъективности, а известный критерий [5] имеет лишь теоретическое значение.

Как для вещественного, так и для комплексного пространства актуальны поиски алгоритмов восстановления.

Для комплексного пространства до сих пор неизвестно минимально возможное количество векторов системы, обеспечивающей восстановление фазы. Довольно давно высказана гипотеза, что такое число равно .

Однако недавно был построен пример системы в R ^A4, состоящей из 11 векторов и допускающей восстановление фазы. Что это: особенность 4-мерного пространства или выражение общей закономерности, неизвестно.

Переходим к рассмотрению другого подхода решения задачи восстановления фазы. Он основан на синтезе идей сжатого зондирования и т. н. «подъема фазы» [8]. Подъем фазы поднимает нелинейную задачу в более высокие размерности и превращает ее в линейную.

Пусть

Вещественные числа предполагаются известными результатами измерения амплитуды.

Определим вещественное -мерное про-

Заметим, что – линейный оператор, и А хх* (п) = Гг[ф*хг*ф_п] = Л (ж)(п).

Полученное равенство показывает, что при таком расширении процесс измерения амплитуды становится линейным за счет увеличения размерности пространства. Добавим теперь к проделанному подъему фазы вероятностные идеи сжатого зондирования. Задача восстановления фазы допускает вероятностную формулировку: минимизировать Г г [^ на множестве неотрицательных матриц       таких, что здесь независимые одинаково распределенные векторы в

В комплексном пространстве в качестве векторов рассматривают векторы с равномерным распределением на комплексной сфере радиуса или с нормальным распределением +i

В вещественном пространстве, соответственно, - равномерное распределение на сфере радиуса или нормальное распределение лг(о, i_My

Теорема [8].

Для всех или точное решение задачи подъема фазы существует с вероятностью >1-о(е^ если количество измерений где и    абсолютные константы.

Таким образом, точное восстановление сигнала с большой вероятностью возможно сразу для всех входящих сигналов.

Если измерения искажены шумом

т

bn = l(x0,

о минимизируется

N

сумма

^jTrt^xj-M на множестве всех неотрицательных матриц

Решение последней задачи (обозначим его

) по случайным векторам равномерного и нормального распределения с вероятностями той же асимптотики, что указана в предыдущей теореме, удовлетворяет оценке

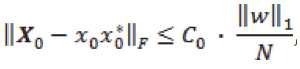
с некоторой абсолютной константой

странство матриц.

Для заданного векторов»

самосопряженных

множества «измерительных определяется оператор

матричного анализа ношениемАН(п) = <Н,<рпф^Н5>

соот- здесь

Работа выполнена при финансовой поддержке Минобрнауки России в рамках базовой части государственного задания, проект №204.

обозначает скалярное произведение Гильберта-Шмидта, индуцирующее матричную норму Фробениуса [9].

Подробнее,

.