Полуаналитический метод расчета упруго-гидродинамического контакта

Введение. В современном мире практически любой инженер, проектирующий подвижную механическую систему, сталкивается с решением контактных задач в узлах трения. Современные тренды проектирования узлов трения летательных аппаратов ставят жесткие условия: максимальное облегчение узла при полном сохранении его прочностных качеств. Одними из самых сложных являются контактные задачи упругогидродинамического взаимодействия двух тел, так как требуют одновременного учета множества факторов, таких как деформация упругих поверхностей, зависящая от давления и температуры вязкость жидкого слоя и вспенивание смазочного материала в зонах низкого давления. Наибольшую сложность в решение упругогидродинамической задачи вносит деформация упругой поверхности, так как при больших нагрузках она существенно влияет на величину геометрического зазора в жидком слое. Существует ряд приближенных аналитических решений таких задач [1–6], полученных в рамках упрощающих допущений, которые не позволяют решить контактную задачу с высокой точностью. В настоящее время широкое распространение получили различные мультидисциплинарные программные CAD/CAE (CAD – Computer Aided Design – компьютерная поддержка конструирования, САЕ – Computer Aided Engineering – компьютерная поддержка инженерного анализа) комплексы (ANSYS, SolidWorks, COMSOL Multiphysics и т. д.). Однако применение таких комплексов для расчета нестационарных упругогидродинамических задач наталкивается на значительные трудности, обусловленные наличием очень тонких слоев, огромными перепадами давления и жесткостью нестационарных задач, требующих выбора очень мелких шагов по времени и пространству. Все это приводит к очень большим вычислительным и временным затратам. В этом случае, для решения конкретных инженерных задач имеет смысл сочетать аналитические методы с ограниченным численным моделированием. Такой подход «гибридного» моделирования позволяет строить полную цифровую динамическую модель проектируемого или же реального узла и изучать его работоспособность при изменении различных внешних факторов. Это особенно актуально для трудно доступных или полностью необслуживаемых узлов, таких как центробежные насосы, использующиеся для систем охлаждения на космических аппаратах [7]. В качестве примера для описания методики решения задач будем использовать подшипник скольжения, схематично изображенный на рис. 1.

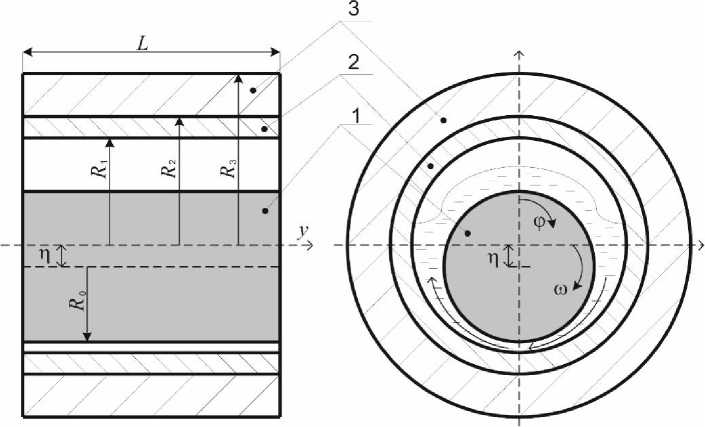
Рис. 1. Геометрическая схема подшипника скольжения: 1 – вал; 2 – бронзовый вкладыш; 3 – корпус

Fig. 1. Geometric diagram of a plain bearing: 1 – shaft; 2 – bronze liner; 3 – case

Здесь ω – угловая скорость вращения вала; φ – азимутальный угол, отсчитываемый в направлении часовой стрелки от точки максимального зазора; η и R 0 – эксцентриситет и радиус цилиндрического вала; R 1 – внутренний радиус вкладыша; R 2 и R 3 – внутренний и внешний радиусы цилиндрического корпуса; L – длина подшипника. В расчетах используем нулевые граничные условия для деформаций на заданной внешней границе корпуса подшипника. Между валом и вкладышем располагается тонкий слой жидкой смазки, называемый смазочным слоем. Также ставим нулевые граничные условия для давления на торцах подшипника.

Разделение упругой и гидродинамической задач. Одним из перспективных путей упрощения общей упругогидродинамической задачи является разбиение ее на последовательно решаемые более простые задачи: гидродинамическую задачу, связанную с определением давления в жидком слое, и контактную задачу, основанную на определении упругой деформации.

Связь упругой деформации и давления в общем виде можно представить в следующем виде:

8( x) = j P (x') K (x - x') dQ ,

n где δ и P – прогиб поверхности и соответствующее давление; Ω – площадка контакта. Функцию K(x – x′), являющуюся ядром линейного функционала, будем называть функцией податливости.

Функция податливости K ( x – x′ ) является ключевым элементом в данном методе решения упругогидродинамической задачи. Важно отметить, что эту функцию можно определить независимо от решения гидродинамической задачи. Так, задавая некоторое распределение давления на границе тел, можно определить соответствующую функцию прогиба δ в результате решения задачи упругости для тел контакта. Далее, при известных функциях δ и P равенство (1) можно рассматривать как интегральное уравнение относительно функции K ( x – x′ ), которое можно решать путем разложения по некоторому ортогональному базису:

K (x - x)=E [Mk Ф k (x - x')+ N Tk (x - x)].              (2)

k = 0

где M k и N k – коэффициенты ортогонального разложения. В большинстве случаев область Ω можно считать прямоугольной и выбирать тригонометрические функции в качестве базисных, для которых справедливы следующие равенства:

Ф k (x - x') = ф k (x )Tk (x)- Tk (x )Ф k (x').T (x - x) = T (x )Tk (x)+ Ф k (x )Ф k (x)

Подставляя (3) в (1), получим следующую систему уравнений

IIФkl12 [Mk (P-Фk)+ N(P'Tk )]=(8-Фt),IITk 112 [Mk (P' Tk )- N (P 'Ф k )] = (8- Tk)

где

II ф k |I² =|T k |Г =(Ф k 'Ф k )=(T_t -T k ) .                        (5)

В результате решения системы (4) вычисляются коэффициенты ортогонального разложения M k и N k , тем самым определяется функция податливости (2). Важно отметить, что восстановление функции податливости является «некорректной задачей» [8], в которой мелкомасштабные погрешности в исходных данных вызывают значительные отклонения в итоговых результатах. Поэтому для сглаживания функции податливости необходимо применять регуляризацию [9].

Расчет давления. Распределение давления P в смазочном слое определяется из уравнения Рейнольдса [10]

div

h— V P

12 ц

= - v ( k h ) +^{d h} 2 ^{V !}   61

где h – толщина жидкого слоя; V – сумма скоростей тел в точке контакта

—►      —*      —*

v = V + v2 .

При этом толщина жидкого слоя h учитывает как геометрический зазор между контактирующими телами h g , так и деформацию упругой 8 поверхности. вызванную избыточным давлением в слое.

2п h = 1 + цcos(ф)+ jP (ф1)K(ф-ф1)dф, P > 0;

V V h = 0. P <  0.

где K (φ-φ’) – функция податливости, не зависящая от распределения давления в слое, но учитывающая геометрические и упругие свойства контактирующих материалов [11].

Заметим, что уравнение (7) учитывает эффект кавитации (вспенивания) для отрицательного давления.

Важно отметить, что вязкость смазочного слоя ц сильно зависит от температуры T и давления P . Существуют множество эмпирических моделей изменения вязкости жидкого слоя [12; 13], однако наиболее точной из них является формула Петрусевича, которая аппроксимирует зависимость вязкости от температуры и давления в экспоненциальном виде:

ц( P, T ) = ц oexp( aP -Ц, T),

где a - пьезокоэффициент, характеризующий изменение вязкости в зависимости от давления; ц о - динамическая вязкость при P 0; Qu так называемый коэффициент крутизны вискограммы.

Тепловой расчет. Расчет мощности тепловыделения Q для подшипника скольжения, работающего в гидродинамическом режиме, определяется выражением

( д P ) 2

Q = —

12 ц (д У J

( д P ) 2

⁺ R 12 Ьф^

₊ Ц V 2 . h

Запишем уравнение теплопроводности в цилиндрических координатах:

1 д ( д T )    1 д ² T „

1 r — l +  —7 = 0.

r д r ( д r J r дф

Решение уравнения (10) можно представить в виде разложения Фурье:

^

T = a0 + Z [ak cos(kФ) + bk sin kФ)] + T0.

k = 1

На внутренней границе при r = R 1 имеем граничное условие для потока тепла из смазочного слоя:

⁹ T

Q = -^Х^Г , д r

где Q – мощность тепловыделения в смазочном слое, определяемая формулой (9). Функцию мощности тепловыделения также разлагаем по Фурье гармоникам:

ГО

Q = ©0 + Z1°k cos(kФ)+ ©k sin( kФ)], k=1 2п                                   2n

0 k = - I Q ( ф )со$( k ф ) d ф ,   © k =- [ Q ( ф )sin( k ф ) d ф , ( k = 1,2,3...);

ⁿ 0                         ⁿ 0

На внешней границе задаем температуру окружающей среды T 0 :

T ( R 3 ) = T o .

Применяя разложение Фурье к формуле (12), получаем уравнения:

।  2n

д ak   „

^-X= © k , о r

—

д b к   ,х

X    = © k .

д r

Здесь коэффициенты a k , b k удовлетворяют дифференциальным уравнениям:

1 д ( дa_k ) k

--1 r—k- l- — a_k = 0, r д r (   д r J r

1 д ( д b_k ) k^г, _n

—I r ^ l--r b_k = 0, r д r (   д r J r ²

1 £| r^ | = о . (16)

r д r (   д r J

Решая уравнения (16), определяем коэффициенты a k и b k :

a k , j = © k , j a k ,   b k , j =© k , j a k ,

ak =

R 3

k

X

f Ri

X k -1

к R 3 j

+

/    x k +1

R к RiJ

k

[ t 1

—

k

X к R i J

RR a_n = —In . 0 x    R i

Нестационарная нагрузка. При резких изменениях внешней нагрузки F возникают возмущения скорости центра масс, вызывающие нестационарные изменения толщины жидкого слоя и распределения давления в зоне контакта. Это приводит к изменению силовой реакции жидкого слоя на внешнюю нагрузку, связанной с давлением уравнением

WW = J PINdx' . (18)

При малых возмущениях скорости центра масс уравнение (18) можно представить в виде разложения

W ' = И ' о ( x c ) — ^ x c .

Здесь левая часть уравнения учитывает стационарную несущую способность W0, а правая – возмущение скорости центра масс, тензорный коэффициент λ представляет собой матрицу коэффициентов демпфирования слоя. Данные коэффициенты определяют релаксацию давления в смазочном слое при нестационарных переходных процессах. Найденные функции стационарной несущей способности и коэффициентов демпфирования позволяют записать уравнение динамики тела в следующем виде:

Mxc + X Xc — W0 (xc) = — F. (20)

Выше изложенный метод позволяет находить самосогласованное нестационарное решение задачи упругогидродинамического взаимодействия тел с любыми геометрическими параметрами и учетом их деформации. На основе данного метода написана программа (подробнее [14]), которая позволяет эффективно вычислять самосогласованное распределение давления в смазочном слое подшипника качения, но, изменяя в ней уравнение зазора в смазочном слое для другого вида контакта, программа становится универсальной.

Сравнение предлагаемого метода расчета с CAD/CAE программами. Расчет смазочного слоя подшипника скольжения (рис. 1) по изложенному выше методу сравниваем с аналогичным расчетом с использованием программного комплекса ANSYS, основанного на методе конечных элементов. Блок-схема расчета для обоих методов представлена на рис. 2.

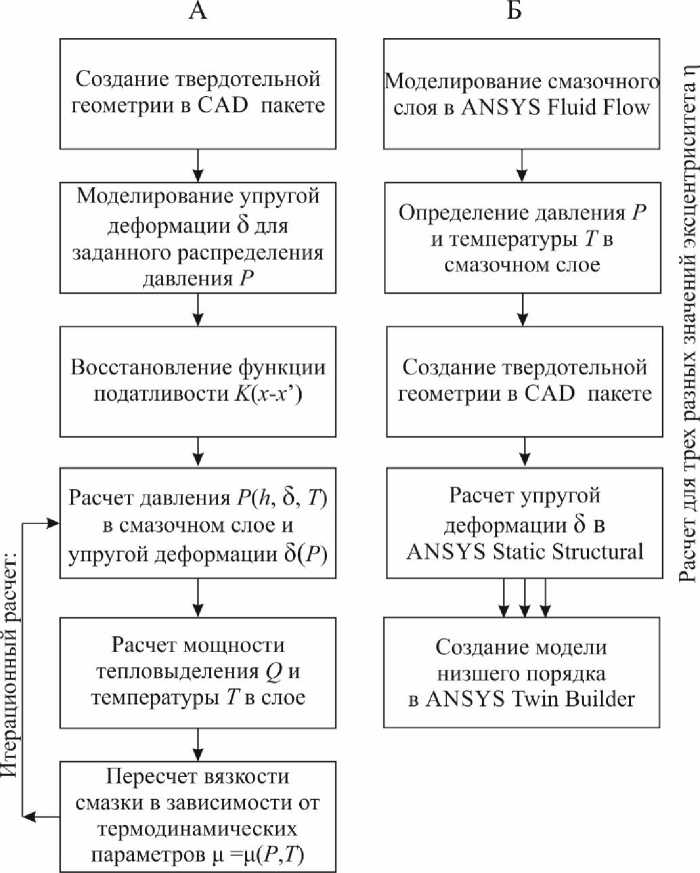
Рис. 2. Блок-схема методов расчета подшипника скольжения;

А – предлагаемый «гибридный метод»; Б – методика расчета в ANSYS

• Fig. 2.    A flowchart of methods for calculating a plain bearing;

A – the proposed "hybrid method"; B – calculation method using ANSYS

Рассмотрим рис. 2 более детально. На первом этапе «гибридного» метода моделируем упругий прогиб подшипника скольжения в программе ANSYS (можно использовать любую другую расчетную программу, это не принципиально) и в качестве нагрузки задаем произвольное распределение давления вдоль поверхности. В результате расчета определяем упругий прогиб вкладыша. На этом использование сложных CAD/CAE программ заканчивается.

Далее, зная распределение давления в смазочном слое и соответствующие упругие деформации, восстанавливаем функцию податливости по методу, описанному выше. После этого переходим к итерационному расчету смазочного слоя [14], который учитывает переменную вязкость смазки, эффект кавитации, изменение температуры в слое и деформацию упругой поверхности. Важно отметить, что данный алгоритм легко реализуется практически в любой программной среде и достаточно быстро и точно производит расчет для любых значений нагрузок и эксцентриситетов.

При выполнении полного расчета в пакете ANSYS сначала нужно смоделировать смазочный слой в ANSYS Fluid Flow, что на первый взгляд не должно вызывать сложностей. Но при значениях относительного эксцентриситета подшипника больше 0,8 возникают трудности в моделировании, так как значение толщины смазочного слоя становится меньше допустимого (10-7 м). При таких значениях большинство CAD/CAE программ выдают ошибку при моделировании и строят поверхность, а не твердое тело. Кроме того, нет возможности в пакетах CAD/CAE учитывать эффект кавитации, что сказывается на максимальном значении давления. С учетом указанных ограничений, моделируем смазочный слой и определяем создаваемое им давление, а также рассчитываем мощность тепловыделения и температуру в смазочном слое.

Далее переходим к моделированию корпуса подшипника, производя те же самые действия, что и при моделировании деформации упругого слоя в «гибридном» методе. Разница заключается лишь в том, что распределение давление по упругому слою импортируется из ранее рассчитанного смазочного слоя. Для перехода к нестационарному расчету нужно произвести расчеты минимум для трех разных смазочных слоев, то есть для трех разных значений относительного эксцентриситета. Полученные результаты импортируем в пакет ANSYS Twin Builder. На основе ранее полученных данных, данный пакет путем численной аппроксимации результатов строит модель подшипника скольжения низшего порядка, которая позволяет в режиме реального времени определять, как изменится прогиб вкладыша и давление в смазочном слое при плавном изменении нагрузки.

Сравним результаты решений (рис. 3), полученные при помощи «гибридного» моделирования и моделирования в пакетах ANSYS и СOMSOL Multiphysics [15]. Расчет выполнялся для следующих параметров: L = 0,125 м; R 1 = 0,25 м; μ = 0,19 Па∙с, относительный эксцентриситет ῆ = 0,5; скорость вращения вала 1000 об/мин.

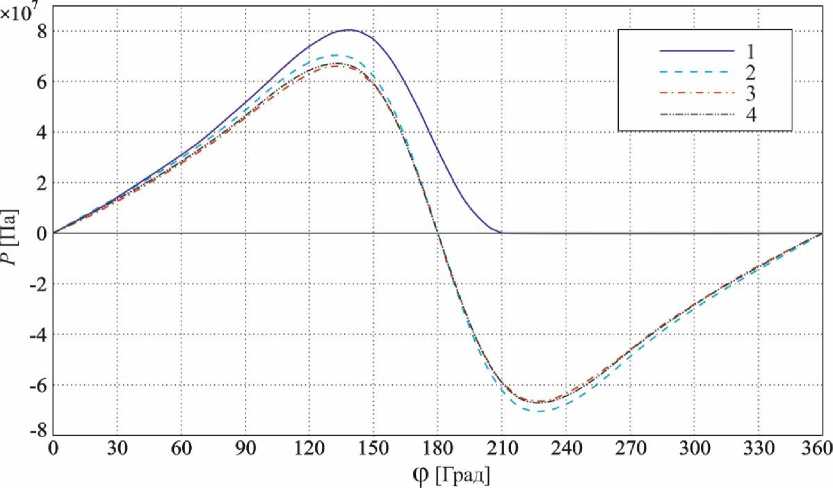
Рис. 3. Давление в смазочном слое подшипника скольжения:

1 – полуаналитическое решение, учитывающее кавитационный эффект;

2 – полуаналитическое решение без учета кавитационного эффекта;

3 – моделирование в СOMSOL Multiphysics; 4 – моделирование в ANSYS

• Fig. 3.    Pressure in the lubricating layer of the plain bearing:

• 1    – semi-analytical solution that takes into account the cavitation effect;

• 2    – semi-analytical solution without taking into account the cavitation effect;

• 3    – modeling in COMSOL Multiphysics; 4 – modeling in ANSYS

Из рис. 3 видно, что расчеты, выполненные в пакетах ANSYS (кривая 4) и СOMSOL Multiphysics (кривая 3), показывают одинаковые результаты (различие не более 1 %). При этом оба расчета не учитывают эффект кавитации, что приводит к снижению максимума давления на 15 % по сравнению с «гибридным» методом расчета, учитывающим кавитационный эффект и исключающим возникновение областей отрицательного давления (кривая 1). Результаты расчета с помощью «гибридного» метода без учета кавитации хорошо согласуются с расчетами в CAD/CAE пакетах, расхождение максимальных давлений в слое не превышает 6 %.

Сравнительный анализ описанных выше результатов позволяет сделать вывод, что полуаналитический «гибридный» метод расчета при своей экономичности показывает хорошую точность расчетов. При этом он имеет ряд преимуществ над численными расчетами в CAD/CAE программах. Первым и довольно весомым плюсом является «стоимость расчета». CAD/CAE пакеты, позволяющие провести ряд описанных выше расчетов и обладающие нужным функционалом, имеют очень высокую стоимость, в то же время для «гибридного» моделирования подойдет любой пакет, умеющий проводить статический расчет (например пакет ANSYS Student). Вторым преимуществом «гибридного» моделирования являются невысокие требования к вычислительным ресурсам, в то время как для расчетов в CAD/CAE пакетах требуются мощные компьютеры, которые так же имеют высокую стоимость. Расчетным и самым важным преимуществом «гибридного» моделирования является возможность нестационарного расчета тяжело нагруженной работы подшипника скольжения или иного вида контактного взаимодействия (методика расчета будет отличаться лишь уравнением зазора для конкретного вида контакта). Во-первых, в «гибридном» моделировании возможно задать любой размер минимального зазора без ограничений для сверхтяжелых нагрузок. При этом моделирование в CAD/CAE пакетах имеет ограничение для минимальных значений зазора. Во-вторых, «гибридное» моделирование позволяет учитывать дополнительные важные физические факторы, сильно осложняющие расчет: эффект кавитации, существенно влияющий на пик давления, переменную вязкость смазочного слоя, зависящую от термодинамических параметров, а также резкий рост пика давления в слое при резком скачке нагрузки. В CAD/CAE пакетах этот скачок не учитывается и рост давления происходит плавно от начального значения к новому, соответствующему изменившейся нагрузке.

Заключение. Предложен метод «гибридного» моделирования, позволяющий с минимальными экономическими и расчётными ресурсами производить расчет нестационарного упругогидродинамического контакта с учетом таких факторов, как деформация упругой поверхности, переменная вязкость смазочного слоя и эффект кавитации. Данный метод расчета может использоваться в различных конструкторских или технологических бюро для предварительной оценки проектируемого узла, оптимизации уже существующего, а также создания цифрового двойника эксплуатируемого узла трения и определения условий его нормальной работы в тех или иных условиях.