Получение кривой намагничивания дисперсии парамагнитных наночастиц путем нахождения намагниченности и намагничивающего поля методом ЯМР

Дисперсии магнитных наночастиц (магнитные жидкости) имеют большие перспективы применения [1, 2], поэтому их исследование является актуальным. Основным свойством магнитных жидкостей, используемым при их практических применениях, является их взаимодействие с магнитным полем, которое в значительной степени определяется кривой намагничивания. Для получения этой кривой обычно используют индукционный метод, в котором намагниченность I определяют путем интегрирования производной d I d H ₀ , измеряемой в переменном внешнем поле H ₀ , а для нахождения стационарного значения I производят экстраполяцию к нулевой частоте [3]. Получаемая экспериментальная зависимость I от H ₀ не описывается теоретической формулой Ланжевена, и для ее объяснения приходится предположить, что с ростом H ₀ эффективный диаметр наночастиц d значительно уменьшается [2]. При использовании предлагаемого метода можно находить зависимость I не от H ₀ , а от напряженности намагничивающего поля H_H . В результате получается кривая намагничивания, адекватная теоретической формуле Ланжевена при неизменном d , что дает возможность по виду этой кривой определять диаметр наночастиц, а также константу эффективного поля λ .

МЕТОД ИЗМЕРЕНИЯ

В предлагаемом методе для определения I и λ используется взаимосвязь напряженности внешне- го магнитного поля H0 , напряженности поля внутри дисперсии H и напряженности намагничивающего поля HH :

H h = H + 1,                  (1)

H = H 0 + (1 - N ) I .             (2)

Экспериментально намагниченность I и константу λ можно находить по формулам (1), (2),

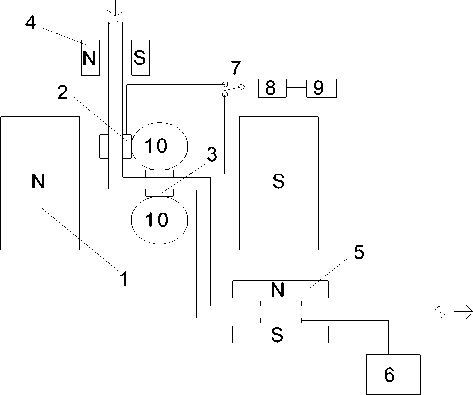
Рис. 1. Схема установки для измерения намагниченности дисперсии парамагнитных наночастиц.

1 — полюса магнита; 2, 3 — катушки датчика нутации; 4 — поляризатор; 5 — анализатор; 6 — детектор сигнала ЯМР; 7 — ключ; 8 — генератор радиочастоты; 9 — частотомер; 10 — образец с магнитной жидкостью измеряя напряженность поля магнита H0 без образца; напряженность HH нормальной индукции внешнего поля снаружи образца вблизи его поверхности и напряженность H в прямоугольной полости, вырезанной в образце параллельно индукции поля [4]. Вследствие малых напряженностей и значительной неоднородности полей для их измерения был применен ЯМР в проточной жидкости (метод нутации) [5].

Схема экспериментальной установки приведена на рис. 1. Она содержит магнит 1, между полюсами которого расположены датчики нутации 2, 3, включенные в проточную водяную магистраль между поляризатором 4 и анализатором 5. Сигнал ЯМР в анализаторе регистрируется прибором 6. Напряжение на катушки датчиков 2, 3 подается через ключ 7 от генератора 8; его частота, измеряемая частотомером 9, пропорциональна напряженностям поля в датчиках.

Рядом с датчиками 2, 3 имеется место для установки образцов 10, заполненных исследуемой магнитной дисперсией. При этом нормальная индукции стенка образца располагается около катушки 2, а катушка 3 оказывается в промежутке между образцами.

При отсутствии в магните образца с исследуемой жидкостью по показаниям частотомера 9 измерялась напряженность H ₀ . Затем в магнит помещались образцы с исследуемой жидкостью и по показаниям частотомера переключением 7 измерялись напряженности h_H в датчике 2 и H в датчике 3.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Предмет исследования — коллоидный раствор в воде наночастиц магнетита с объемной концентрацией твердой фазы C = 2.7 %. Измерялись значения H и H_H при разных напряженностях H ₀ . На рис. 2 точками представлена полученная по формуле (1) экспериментальная зависимость I = H H - H от H H . Она должна соответствовать теоретической формуле

I = ^La (% ),                (3)

где I_H — намагниченность насыщения; La ( ^ ) =

= cth ^ -— — функция Ланжевена; £ = a ■ H_H ; a — ξ ^H коэффициент, определяемый эффективным магнитным моментом наночастицы P_m

µ0Pm a ;

KT

µ ₀ , K , T — магнитная постоянная, постоянная Больцмана, температура.

Так как экспериментальная кривая намагничивания, найденная электромагнитным методом, в которой принято H H = H 0 , согласуется с теорией Ланжевена только при условии, что в формуле (4) коэффициент а при £ <  0.5 на 80-100 % больше, чем при £ >  1 [2], определим значения а , при которых формула (4) соответствует начальному и конечному участкам экспериментальной зависимости, представленной на рис. 2.

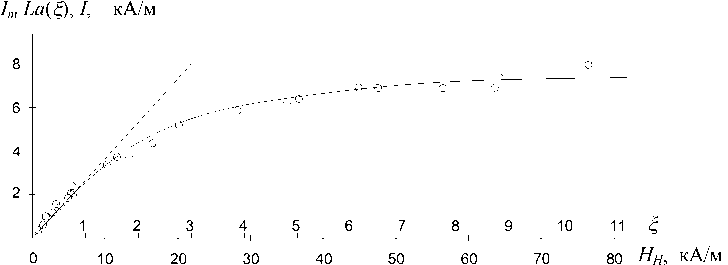
Рис. 2. Экспериментальная зависимость I = H H - H от H H (точки) и теоретическая зависимость I = I m La( ^ ) (линия)

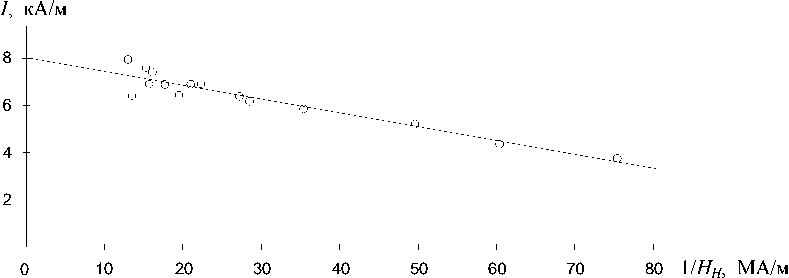
Рис. 3. Экспериментальная зависимость I от 1/ H H

Для определения а при ^ >  1 на рис. 3 по 15 точкам рис. 2 построена экспериментальная зависимость I от 1 H_H . Методом наименьших квадратов зависимость рис. 3 можно представить эмпирическим выражением

I — a —

b

HH

где а — 8026 А/м, b — 58.35 - 10 6 А ²/ м² .

Согласно (3), зависимость (5) можно с достаточной точностью представить теоретической формулой

I ^— I H

—

ξ

^— I H

—

I H

αHH

Сравнив (5) и (6), находим намагниченность насыщения исследуемой дисперсии I_H — а — 8026А/м и коэффициент а — IH/b — 13.7 - 10 ^{— 5}м/А. Следует отметить, что полученное значение I_H близко к значению I_H — 8100А/м, найденному для этой же дисперсии при значительно большей напряженности H ₀ [6].

Для определения а при £ <  0.5 на рис. 2 про-

ведена касательная к начальному участку экспериментальной кривой намагничивания. Ее угловой коэффициент, рассчитанный методом наименьших квадратов по первым 10 экспериментальным точкам, составил c — 0.365. Согласно (3), при § <  0.5

зависимость I от H_H можно представить в виде I — I_H^/ 3 — I_HаH_H /3, откуда угловой коэффици

ент c —

d I

Iα

— —— и а —

3 c

— 13.6 - 10 ^{— 5}

м

d H    3        I          А

HH

Таким образом, на начальном и конечном участках кривой намагничивания α имеет практиче-

ски одинаковые значения. Зная α и H_H , можно найти значения ^ — аН_Н и, подставляя ^ в (4), построить теоретическую зависимость I от H_H , представленную на рис. 2 сплошной кривой. Можно констатировать, что экспериментальная зависимость адекватна формуле Ланжевена при постоянном α .

Подставив полученное значение α в (4), находим магнитный момент P m — 4.4 - 10 ^{— 19}А - м². Он связан с диаметром частиц d :

P m — I m в , (7) 6

где I M — 4.5 - 10 5 А/м — намагниченность насыщения магнетита, в — 0.8 — содержание магнитной составляющей в твердой фазе [2]. Подставив значения в , P m , I M в (7), находим d ® 13.3 нм. Эта величина превышает d = 8.1 нм и d = 10.8 нм, полученные на начальном и конечном участках кривой намагничивания электромагнитным методом [2].

Пользуясь формулами (1), (2), можно найти константу эффективного поля:

Л — H — H ⁰ + N . (8) Н н — Н

На рис. 4 приведена найденная по экспериментальным результатам и формуле (7) зависимость величины λ от напряженности внешнего поля H ₀ . (Для использованного в эксперименте цилиндрического образца с осью, нормальной H ₀ , принято N = 0.5 [7]). Из рисунка видно, что величина λ практически не зависит от H ₀ , и ее среднее значение составляет около 0.23, что соответствует значению, полученному в сильном поле [8]. Разброс экспериментальных точек на рис. 2, 3 можно

λ

0.3

0.2

0.1

0       10       20       30       40       50       60       70

H , кА/м 80      ⁰

Рис. 4. Экспериментальная зависимость λ от H ₀

объяснить эффектом гистерезиса намагниченности, вызванного структурообразованием в дисперсии наночастиц [8].

ЗАКЛЮЧЕНИЕ

Несоответствие формуле Ланжевена экспериментальной кривой намагничивания, получаемой электромагнитным методом, можно объяснить двумя причинами.

• 1.    Построением кривой намагничивания в виде зависимости I от напряженности внешнего поля H ₀ , в то время как формула Ланжевена подразумевает зависимость I от напряженности намагничивающего поля H_H .

• 2.    Определением I не из классической зависи

мости (1), а по формуле I = — - H 0 .

µ ₀

Полученное в настоящей работе соответствие теории и опыта показывает, что если строить зависимость I от напряженности намагничивающего поля H_H = H ₀ + (1 + 1 - N ) I , а намагниченность находить из классической зависимости (1), то экспериментальная зависимость получается адекватной формуле Ланжевена.

Выводы

Таким образом, предлагаемый метод определения намагниченности, основанный на измерении методом нутации внешнего и внутреннего магнитных полей в магнитной жидкости, позволяет оценивать диаметр наночастиц магнетита, константу эффективного поля и дает перспективу исследования влияния структурообразования на внутренние магнитные поля.