Получение примеров точных решений уравнений Навье-Стокса для винтовых течений методом суммирования скоростей

Недавно была обобщена теорема Томсона [1] о сохранении циркуляции по контуру, состоящему из одних и тех же частиц идеальной баротропной жидкости. Для небаротропной и вязкой жидкости найдена скорость движения воображаемых частиц. При этом движении сохраняется циркуляция скорости жидкости по контуру, состоящему из воображаемых движущихся частиц [2].

Этот новый закон сохранения еще не заложен в основу численных методов. Поэтому в работе [2] предложено использовать его для проверки численных расчетов. Численные решения, как правило, получаются с некоторой ошибкой – с некоторым отклонением от точного решения. Точное выполнение закона сохранения на численном решении невозможно. Для выбраковки неприемлемых решений необходимо решить вопрос о величине ошибки, превышение которой свидетельствует о нарушении закона сохранения.

Вопросы подобного рода еще не изучались. В качестве первого шага предполагается провести ряд численных экспериментов для выяснения точности, с которой выполняется закон сохранения [2] в случае, когда численное решение имеет некоторую «приемлемую» точность. В рамках такого эксперимента требуется вычислять как ошибку выполнения закона сохранения, так и отклонение численного решения от точного решения. Для этого требуется запас различных точных решений. Следует заметить, что некоторые точные решения трудно реализовать в эксперименте или наблюдать в реальной обстановке. Это связано со сложностью создания граничных условий (которые должны быть взяты из самих решений). Но если речь идет о верификации, то есть о проверке точности численного алгоритма, не обязательно иметь техническую возможность реализовать краевые условия в эксперименте. Большинство численных алгоритмов работают с любыми граничными условиями. Поэтому для упомянутых выше численных экспериментов можно использовать и такие точные решения, для которых трудно создать реальные граничные условия, и которые до сих пор считались практически непригодными. К ним относятся точные нестационарные решения уравнений Навье–Стокса, полученные методом Тркала из стационарных винтовых решений уравнений Эйлера. Винтовыми в настоящей статье называются решения, у которых векторы скорости и завихренности связаны постоянным по пространству и времени скалярным коэффициентом. Тркал в статье [3] в общем пространственном случае показал, что для несжимаемой жидкости скорость стационарного винтового решения уравнений Эйлера, умноженная на exp( -at ), где t - время, при надлежащем выборе параметра a будет удовлетворять уравнениям Навье–Стокса. Считается [4], что этот результат Тркала является логическим продолжением идей, высказанных Тейлором и Кальдонаццо. В качестве стационарных винтовых решений уравнений Эйлера можно использовать, например, ABC -решение или осесимметричные решения Громеки–Бельтрами [5, 6], которые были получены независимо Громекой и Бельтрами в 1881 и в 1889 годах соответственно. (Текст [5] можно найти в [7].) В этих решениях проявляется сложное взаимодействие движений жидкости в разных направлениях. Однако решения Громеки–Бельтрами имеют ось симметрии, а ABC -решение обладает свойством периодичности: оно состоит из одинаковых кубических ячеек.

Отметим, что известны и другие винтовые решения – точные решения Богоявленского, обладающие кристаллографической симметрией [8–10]. Этот класс течений описывает солитонные течения на сфере, которые в общем случае являются квазипериодическими по координатам [8–10]. Кроме того, в недавней работе [11] приведены новые геометрические алгоритмы построения винтовых векторных полей. Это позволило построить новые классы точных винтовых решений уравнений Эйлера [12].

Представляется, что результаты численных экспериментов по выяснению «приемлемой» точности будут более информативными, если в запас точных решений включить точные решения с более сложной структурой, в которой нет симметрии и периодичности. Для этого в данной работе предложено использовать метод получения таких сложных решений, названный методом векторного суммирования. Этот метод был известен ранее для винтовых решений уравнений Эйлера. Основная научная новизна данной работы состоит в обосновании возможности использовать этот метод для винтовых решений уравнений Навье–Стокса.

С теоретической точки зрения метод векторного суммирования очень прост. Но его практическая реализация связана с громоздкими формулами, которые невозможно найти в одной книге. Учитывая это, в четвертом разделе и в Приложениях приведены справочные сведения, достаточные для компьютерного представления новых точных решений, и приведен пример представления одного из таких решений. Это сделано для того, чтобы данную статью можно было использовать как пособие по построению новых точных решений с целью верификации компьютерных программ.

Для знакомства с теоретической частью данной статьи можно опустить чтение четвертого раздела и Приложений.

• 2.    Уравнения движения

Рассмотрим течение ньютоновской вязкой несжимаемой жидкости в потенциальном по ле массовых сил. Будем использовать следующие безразмерные переменные: V - скорость; Q = rotV - завихренность; p - давление, отнесенное к плотности; П - потенциал объемных сил; Re - число Рейнольдса, t - время. С учетом равенства A V = — rot Q , верного для несжимаемой жидкости, движение описывается уравнениями Навье–Стокса в форме [1]:

V + — rot Q + Q х V = — dt Re

V p + V- +П , div V = 0 .

В случае д V = 0 при нулевой вязкости эти уравнения упрощаются и принимают вид уравнений Эйлера для несжимаемой жидкости [13]:

V ^-

Q х V = —V р + —+П , div V = 0 .

Здесь и далее знак волны над символом означает, что речь идет о решении уравнений Эйлера.

В данной работе уравнения (1) и (2) будут рассматриваться в ограниченной замкнутой области. Все выкладки и рассуждения будут проводиться в предположении, что компоненты скорости, давление и потенциал объемных сил имеют непрерывные вторые производные по пространственным координатам и непрерывные первые производные по времени. Чтобы далее не обсуждать вопросы гладкости функций, заметим, что это требование для компонент скорости и для давления будет выполнено в полученных ниже точных решениях при условии, если оно будет выполнено для потенциала объемных сил.

• 3.    Получение точных решений уравнений Навье–Стокса методом Тркала

Говорят, что скорость V удовлетворяет уравнениям Навье-Стокса (уравнениям Эйлера), если существует давление p, составляющее вместе с этой скоростью решение уравнений Навье-Стокса (уравнений Эйлера). Соленоидальность (div V = 0) является необходимым условием того, чтобы скорость удовлетворяла уравнениям Навье–Стокса. Но этого недостаточно. Если взять произвольную соленоидальную скорость, то может оказаться невозможным «подобрать» соответствующее давление p. Поэтому не всякая соленоидальная скорость удовлетворяет уравнениям Навье–Стокса. Аналогичная ситуация имеет место и для уравнений Эйлера.

В данной работе исследуются винтовые решения. Это решения, в которых

Q = rot V = k V , k = const .

(Здесь равенство k = const означает постоянство и в пространстве и во времени.) Скорость, удовлетворяющую условию (3), будем называть винтовой.

Заметим, что винтовые решения являются подклассом течений Бельтрами, в которых

Q x V = 0, а величина k, вообще говоря, зависит от пространственных координат и времени.

Для винтовых течений уравнения Навье–Стокса (1) и уравнения Эйлера для стационарной скорости (2) имеют соответственно вид

V + -1 rot Q = -V Рр + V- +ПІ , div V = 0 ,

∂t Re                  2

и

0 = -V

"    V - p˜ + 2 +Π

nz

, div V = 0 .

Из уравнения (5) следует важный для поиска точных винтовых решений вывод, позволяющий при поиске скорости точного решения исключить из рассмотрения давление и потенциал объемных сил. Для винтовых решений поиск стационарной скорости, удовлетворяющей уравнениям Эйлера для несжимаемой жидкости, сводится к поиску стационарной скорости V, удовлетворяющей уравнению (3) и уравнению неразрывности div V = 0. Если такая скорость найдена, то давление может быть вычислено по формуле р = ро -

V-

^{- п} ,

где p ˜ 0 – произвольная константа, обеспечивающая неотрицательность давления p ˜ в рассматриваемой области течения. Выбор такой константы p ˜ 0 всегда возможен в ограниченной замкнутой области в силу требований к гладкости, сформулированных в конце второго раздела. Существование давления (6), удовлетворяющего уравнениям (5), означает, что скорость V удовлетворяет уравнениям Эйлера. Такие решения ( V ,р~) будем называть стационарными винтовыми решениями уравнений Эйлера.

Метод Тркала. Пусть р, V и Q = rotV = k V - давление, скорость и завихренность винтового решения уравнений Эйлера со стационарной скоростью. Рассмотрим зависящую от времени скорость V = V exp( -tk ^- /Re). Эта скорость соленоидальна, поскольку div V = exp( -t k ^- /Re) div V = 0. Завихренность этой скорости

Q = rotV = rotV exp( - tk ^- / Re) = k V exp( - tk ^- / Re) = k V .

Следовательно, для скорости V выполнено условие (3) и rot Q = k ^- V .

Поэтому левая часть (4) равна

∂       1                k ²                        k ²

dt ^{V +} Re ^rotQ = ^- Re ^V exp^{( -}tk ^{/ R}e) ⁺ Re ^V = ° .

Правая часть (4) будет равна нулю, если давление вычислить по формуле

V ²

p = p о - “2“

- П = p о--— exp( - 2 1 k ^- / Re) - П .

Таким образом, ( V , p ) будет винтовым решением уравнений Навье-Стокса. Такой способ получения решений уравнений Навье–Стокса предложен Тркалом в [3].

Обратим внимание на отличие давлений р и р. При постоянном во времени поле П давление р непостоянно во времени и вычисляется по формуле (7), а давление р не зависит от времени и вычисляется по формуле (6).

Итак, каждому стационарному винтовому решению уравнений Эйлера соответствует нестационарное винтовое решение уравнений Навье–Стокса. Учитывая это, будем искать скорость V стационарных винтовых решений уравнений Эйлера. И не будем каждый раз напоминать, что скорость V = V exp( —tk ² /Re) и давление, вычисленное по формуле (7), будут решениями уравнений Навье–Стокса.

• 4.    ABC -решение и решения Громеки–Бельтрами

Напомним известные способы суммирования стационарных винтовых решений на примере ABC -решений и решений Громеки–Бельтрами.

ABC-решение. Пусть Oxyz - прямоугольная декартова система координат; i, j, k - базисные векторы этой системы. И пусть A, B, C,k - произвольные константы. Непосредственной проверкой можно убедиться, что если u = A sin( kz) + C cos( ky), v = B sin(kx) + A cos(kz),                               (8)

w = C sin(ky) + B cos(kx), то скорость V = u i + v j + w k будет удовлетворять уравнениям div V = 0 и rot V = k V. То есть V будет скоростью винтового решения уравнений Эйлера. В виде (8) это решение предложено в [14]. Однако частные случаи ABC -решения были известны значительно раньше. Например, в 1919 году (для случая A = 1, B = C = 0) оно было приведено в статье [3] в качестве примера винтового течения.

Суммирование ABC -решений. Различным наборам чисел A, B , C, k соответствуют различные винтовые решения. Сумма решений, соответствующих наборам A 1 ,B 1 ,C 1 ,k 1 и A 2 , B 2 , C 2 , k 2 , в случае k 1 = k 2 дает новое винтовое решение, соответствующее набору A 1 + A 2 , B 1 + B 2 , C 1 + C 2 , k 1 . Если же k 1 = k 2 , то суммарная скорость не будет винтовой скоростью и в общем случае не будет удовлетворять уравнениям Эйлера.

Решения Громеки–Бельтрами. Введем цилиндрическую систему координат r, ϕ, χ с началом в точке Ө и будем рассматривать симметричные относительно оси Ө х течения. «Необычное» использование греческих букв Ө и х объясняется тем, что в следующем разделе эта система координат будет рассматриваться одновременно с прямоугольной декартовой системой координат Oxyz , оси которой могут не совпадать с осью Ө х •

Параметры осесимметричного течения не зависят от окружной координаты ϕ . Пусть e r , e , , e х — правая тройка единичных векторов в радиальном, окружном и осевом направлениях соответственно. Вектор скорости закрученного ( V , = 0) течения имеет вид:

V = Vr er + V,e, + Vxex, где функции Vr, V,, Vx зависят от r, х и не зависят от ^. Пусть k - произвольная константа, а функция ф = ф (г, х) удовлетворяет уравнению

/ (1 ^) + д (1 ^) = —k2 Ф, r> 0-(9)

∂r r ∂r     ∂χ r ∂χ r

В работах [5, 6] показано, что для произвольного потенциала П = П ( г, х ) набор функций

Vr =1(10)

r ∂χ

• V, = —kr,(11)

Vx = —1 дФ,(12)

r ∂r р — po — 0.5 (V2 + V,2 + VX2) — П является винтовым решением уравнений Эйлера, а функция ф = ф(г, х) постоянна вдоль линий тока и поэтому называется функцией тока.

Таким образом, любое решение уравнения типа (9) «порождает» точное винтовое решение уравнений Эйлера для несжимаемой жидкости.

Все решения уравнения (9) до сих пор не найдены. Громека [5] и Бельтрами [6] искали решения в виде произведения ф = ф ( r, х ) = R ( r )X( х ) (метод разделения переменных). Но в их статьях представлены не все решения, которые можно получить таким методом. Во-первых, они не рассматривали решения, которые имеют особенность на оси симметрии. Во-вторых, статьи Громеки и Бельтрами опубликованы в то время, когда еще не были исследованы цилиндрические функции мнимого аргумента (Macdonald functions). Поэтому в статьях Громеки и Бельтрами отсутствуют решения, которые выражаются с использованием таких функций.

Приведем все известные в настоящее время решения (9), которые можно получить методом разделения переменных. Все эти решения следует называть решениями Громеки–Бельтрами.

Для каждого фиксированного числа к = 0 решением ф = ф(г, х) уравнения (9) является произвольная линейная комбинация функций вида rIi(p 1 r) sin(m 1 х),    rI1(P 1 r) cos(m 1 х),    m i = к2 + P2;

rK i ( P 2 r ) sin( m 2 х ) ,  rK i ( p 2 r ) cos( m 2 х ) ,  m 2 = к ² + P 2 ;

rJ i ( P 3 r ) sin( m 3 х ) ,   rJ i ( P 3 r ) cos( m 3 х ) ,   m 3 = к ² - P 2 ;

rY l ( p 4 r ) sin( m 4 х ) ,  rY l ( p 4 r ) cos( m 4 х ) ,   m 4 = к ² — P 4 ;

rJ i ( P 5 r ) exp( m 5 х ) ,  rY l ( p 5 r ) exp( m 5 х ) ,    m 5 = p 5 - к ² ;

sin( кх ); cos( кх ); r ² sin( кх ); r ² cos( кх ); rхJ i ( |к| r ); r хY l ( |к| r ) ,          (13)

где p 1 p 2 – произвольные положительные константы, а константы p 3 ,p 4 ,p 5 положительны и выбраны так, что p 3 < к ² , p 4 < к ² , p 5 ф к ² . J 1 , Y l - функции Бесселя и Неймана первого порядка; I ₁ и K 1 – цилиндрические функции мнимого аргумента первого порядка.

Некоторые из приведенных выше решений Громеки–Бельтрами имеют особенность на оси симметрии. Они могут использоваться для тестирования программ расчета течений в зазоре между двумя соосными поверхностями вращения. Такие течения не содержат ось симметрии.

Суммирование решений Громеки–Бельтрами с общей осью симметрии. Приведем пример применения известного метода суммирования винтовых решений с общей осью симметрии. Этот метод указан в работах [5, 6] и основан на возможности сложения различных решений уравнения (9), полученных для одинаковых значений коэффициента k . Рассмотрим линейную ко м бинацию двух функций тока для случая к = 2: ф ' = rJ i (V3 r ) sin( х ) и ф" = rJ i (V5 r ) exp( — х )• Соответствующие скорости /                                                                ''

V = V' e _r + V ^ , e ф + V ^ e _x и V = V'' e _r + V ^ ' e ^ + V X ' e _x вычисляются по формулам (10) -(12):

1 дф

V-(г,х) = -ф-= = J1(V3r) cos (х),V'(г,х) = —к— = — 2Ji(V3r) sin(х), r r ∂χ                      ϕ

VX((г,х) = — -^-ф’1 = —V3Jo(V3r) sin(х);(14)

r ∂r

V ' ' ( г,х ) = — J i ( V 5 r ) exp( —х ) ,V ^^ ( г,х ) = — 2 J i ( V s r ) exp( —х ) ,

VX(г,х) = —V5Jo(V5r) exp(—х),(15)

где J0 – функция Бесселя нулевого порядка. На рис. 1 показаны в осевой плоскости линии '''

тока радиально-осевых скоростей Vrx = V'er + Vxex и Vrx = V'er + V'ex каждого из этих течений.

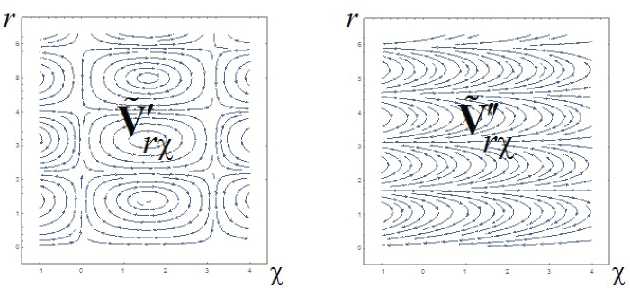
Рис. 1. Линии тока радиально-осевых скоростей в осевой полуплоскости

„                         Ст' Ст11

Оба поля скорости V и V имеют общую ось симметрии и одинаковый коэффициент 1           // к = 2. В силу линейности уравнения (9) сумма скоростей V = V + V соответствует функции ^ = ^' + ^" = rJi(V3r) sin(x) + rJ1 (V5r) exp( — x) и поэтому является решением уравнений Эйлера. Линии тока суммарного течения изображены в двух разных масштабах на рис. 2. (Этот пример и рис. 1 и 2 заимствованы из статьи [15]).

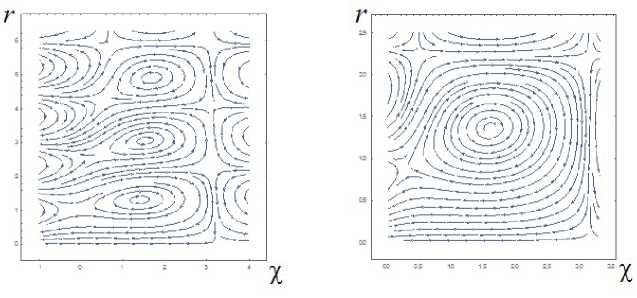
Рис. 2. Линии тока суммарного течения в осевой полуплоскости в разных масштаба

Этот пример показывает, что различные линейные комбинации скоростей стационарных винтовых решений уравнений Эйлера с общей осью симметрии и с одинаковым коэффициентом k могут давать различные и интересные сложные течения. Еще раз заметим, что возможность получать новые решения с помощью такого суммирования давно известна [5, 6]. При этом все суммарные решения остаются осесимметричными.

• 5.    Векторное суммирование решений

Рассмотрим две разные прямоугольные декартовы системы координат Oxyz и Oxy z.

Л Л Л

z ^ z

Пусть i , j , k и i , j , k - базисные векторы этих систем координат. Пусть, далее, A, B, C,k -произвольные скалярные константы. Запишем ABC -решение в системе Oxyz:

u = A sin( kz) + C cos( ky ) , v = B sin( kx ) + A cos( kz ) , tz = C sin( ky ) + B cos( kx ) .

w            Z4         Z4           Zs

Вектор скорости V = u i + v j + wz k может быть представлен через базисные векторы i,j,k, то есть может быть представлен в виде: V = u i + vj + w k. В Приложении 1 приведены формулы для расчета компонент u, v, w через координаты x, y, z. В общем случае точки O л л л

с

и O могут не совпадать, а тройки базисных векторов ij , k и i , j , k могут иметь произвольное взаимное расположение. Поэтому в системе Oxyz скорость V = u i + v j + w k является «сдвинутым и повернутым» ABC -решением. В Приложении 1 показано, что в общем случае взаимного расположения систем координат Oxyz и Oxyz невозможно подобрать константы A, B , C, k так, чтобы компоненты u, v, w оказались представлены в виде (8). То есть в системе координат Oxyz скорость V = u i + v j + w k в общем случае не будет являться ABC -решением (поскольку в общем случае ее невозможно записать в виде (8)). Поэтому формально можно считать, что «сдвинутое и повернутое» ABC -решение является новым точным решением для тестирования численных алгоритмов. Однако по своей физической сущности это решение остается ABC -решением. В частности, оно, как и «классическое» ABC -решение, состоит из периодически расположенных одинаковых ячеек с одинаковыми картинами течения.

Аналогичная ситуация имеет место для решений Громеки–Бельтрами. Для те- стирования численного алгоритма можно «замаскировать» осесимметричность решения Громеки–Бельтрами. Достаточно расположить ось симметрии решения Громеки–Бельтрами так, чтобы она не совпадала с осями прямоугольной декартовой системы координат Oxyz. А затем выразить компоненты скорости и давление через x, y, z. Техника такого представления описана в Приложении 1. Компьютерная программа не сможет воспользоваться осесимметричностью решения.

У такого подхода есть один существенный недостаток. Дело в том, что ось симметрии хотя и «замаскирована», но все-таки существует. Поэтому в течении могут отсутствовать процессы, которые имеют место в общем пространственном случае. В этой связи заметим, что симметрия иногда существенно упрощает свойства течения. Так, например, в статье [16] для осесимметричных течений вязкой жидкости удалость получить аналоги теорем Гельмгольца о вихрях, которые в общем пространственном случае верны только для идеальной жидкости.

Предложим способ получения несимметричных и непериодичных (по пространственным координатам) решений. То есть непериодичных течений, у которых нет оси симметрии, нет плоскости симметрии и нет центра симметрии. Как было показано выше, разные ABC -решения с одинаковым коэффициентом k в уравнении (3) можно складывать и получать в результате новое ABC -решение. Это эквивалентно сложению векторов скорости ABC -решений, записанных в одной системе координат Oxyz . Аналогичным свойством обладают решения Громеки–Бельтрами (с одинаковым коэффициентом k ). Получение функции тока нового решения Громеки-Бельтрами сложением двух функций тока ф ' и ф '' эквивалентно сложению векторов скорости решений Громеки–Бельтрами, имеющих общую ось симметрии. Оказывается, что такая возможность сложения векторов является следствием более общего свойства, присущего всем винтовым течениям.

Пусть V 1 и V 2 - две соленоидальные винтовые скорости с одинаковым коэффициентом k :

div V 1 = div V 2 = 0 , rot V 1 = k V 1 , rot V 2 = k V 2 , k = const .

Например, V 1 может быть скоростью ABC -решения, а V 2 - скоростью одного из решений Громеки–Бельтрами. (У этих решений должны быть равны коэффициенты k .)

Рассмотрим векторную линейную комбинацию V = a V 1 + b V 2 , где а и b - произвольные скалярные константы. Она соленоидальна:

nz            nz                        nz                      nz div( a V1 + b V2) = a div V1 + b div V2 = 0, или divV = 0.

Завихренность этой скорости равна nz            nz                          nz                         nz                    nz                 nz              nz rot (aV1 + bV2) = rot (aV1) + rot (bV2) = akV1 + bkV2 = kV, или rot V = к V. (17)

Как показано в третьем разделе (абзац после формулы (5)), условий (16) и (17) достаточно, чтобы скорость V являлась скоростью винтового решения уравнений Эйлера. Поэтому любая векторная линейная комбинация скоростей винтовых решений уравнений Эйлера с одинаковым коэффициентом k в уравнении (3) является скоростью винтового решения уравнений Эйлера с тем же коэффициентом k .

В частности, это означает возможность суммирования скоростей решений Громеки–Бельтрами со скоростями ABC -решений, а также возможность суммирования скоростей нескольких решений Громеки–Бельтрами с несовпадающими осями симметрии. Представляется естественным назвать такой метод получения новых винтовых решений методом векторного суммирования . Заметим, что метод векторного суммирования «автоматически» распространяется на решения уравнений Навье–Стокса, полученные методом Тркала.

Несмотря на то, что метод векторного суммирования давно известен для винтовых течений идеальной несжимаемой жидкости [17], возможность его использования для вязких течений не была замечена ранее и представляется впервые в данной работе. Так, например, в статьях [18, 19] обсуждалась возможность суммирования различных решений уравнений Навье–Стокса. Авторы этих статей указывают лишь на возможность умножения на константу. Другими словами, они заметили, что V = a V i будет скоростью винтового решения уравнений Навье-Стокса, если V i является скоростью винтового решения уравнений Навье-Стокса. Однако «полноценная» линейная комбинация V = a V i + b V 2 винтовых решений в работах [18, 19] не исследована.

Для практического использования метода векторного суммирования можно записывать разные винтовые решения уравнений Эйлера в одной прямоугольной декартовой системе координат Oxyz . И затем складывать компоненты скоростей этих решений.

Продемонстрируем возможности метода векторного суммирования на примере. Сложим компоненты скоростей трех решений с одинаковым коэффициентом к = 2 в одной прямоугольной декартовой системе координат Oxyz .

Первое решение. Это решение Громеки-Бельтрами, соответствующее функции ф ' , рассмотренной выше в четвертом разделе. Ось симметрии Ө ' х ' этого решения совместим с осью Oz так, как это показано на рис. 3. (Единичный вектор e х , направленный вдоль оси Ө ' х ' , в базисе i , j , k основной системы координат представляется в виде: e х = 0 • i + 0 • j + 1 • к .) В цилиндрической системе координат Ө ' ХХХ функция тока ф ' имеет вид ф ' = ф ' ( т ' , Х ) = т ' J i (V3 т ' ) sin( х ' ).

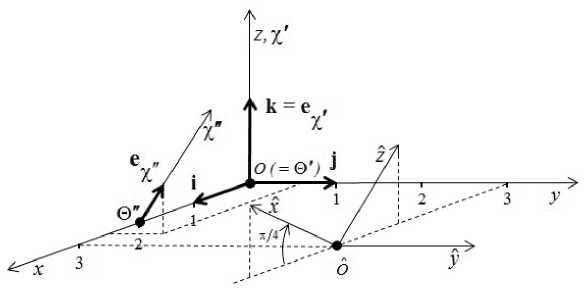
Рис. 3. Расположение осей трех решений в системе координат Oxyz

Второе решение. Это решение Громеки-Бельтрами, соответствующее функции ф " , рассмотренной в четвертом разделе. Зададим еще одну цилиндрическую систему координат Ө '' т '' X ' Х ' . Точку Ө ” расположим так, чтобы в системе Oxyz она имела координаты (2 , 0 , 0).

Единичный вектор e х ", направленный вдоль оси Ө "х" , в базисе i , j , k основной системы координат зададим следующим образом: e у, = 1/V3 • i + 1/V3 • j + 1/V3 • k . Положение оси Ө "х" показано на рис. 3. В цилиндрической системе координат Ө "г" ф"Х' функция тока ■ф " имеет вид: ф " = ф ” ( r " ,Х ) = r " J 1 ( V 5 r " ) exp( — х" )•

Третье решение. Это «сдвинутое и повернутое» ABC -решение, которое является «классическим» ABC -решением с параметрами А = 1 , B = 2 , ( 7 = 3 , к = 2 в системе координат Oxyz. Систему координат Oxyz расположим следующим образом. Точку O расположим так, чтобы в системе Oxyz она имела координаты (3 , 3 , 0). Оси системы OXyz получим вращением осей системы Oxyz вокруг оси Oy на угол п /4 , как показано на рис. 3.

Компоненты скоростей этих трех винтовых решений в системе Oxyz обозначим соответственно u ' , v ' , w ' , u " , v " , w " и u, v, w . Эти три скорости являются соленоидальными винтовыми скоростями с одинаковым коэффициентом к = 2. Поэтому их сумма

'V s = ( u ' + u " + u ) i + ( v ' + v " + v ) j + ( w ' + w " + w ) k (18)

является скоростью винтового решения уравнений Эйлера с тем же коэффициентом k . В Приложении 2 получены формулы для вычисления u ' , v ' , w ' , u '' , v '' , w '' и u, v, w через координаты x,y,z . Представлять отдельно громоздкие формулы для величин ( u ' + u '' + u ) , ( v ' + v " + v ) и ( w ' + w '' + w ) представляется излишним. Поэтому будем считать, что в Приложении 2 получены формулы, выражающие компоненты скорости (18) в системе Oxyz , через координаты x, y, z .

Для произвольного потенциала внешних массовых сил П = П(x, y, z, t) давление p = p о — П — V S/2(19)

и скорость (18) вместе будут составлять винтовое решение уравнений Эйлера.

При этом скорость

'V s exp(—41/Re)(20)

и давление

"V 2

p = p0--2s exP(—81 /Re) — П(21)

вместе будут составлять винтовое решение уравнений Навье–Стокса.

Таким образом, формулы Приложения 2 вместе с формулами (18) и (19) дают новое винтовое решение уравнений Эйлера. А вместе с формулами (18), (20) и (21) – новое винтовое решение уравнений Навье–Стокса. Это новое решение не периодично. У него нет оси симметрии, нет плоскости симметрии и нет центра симметрии.

• 6.    Заключение

• 7.    Приложение 1. Представление решений в прямоугольной декартовой системе координат

Показано, что линейная комбинация скоростей нестационарных решений уравнений Навье–Стокса, полученных методом Тркала, с одинаковым коэффициентом k в уравнении (3) является скоростью некоторого нестационарного решения уравнений Навье–Стокса. Такой метод получения новых винтовых решений предложено называть методом векторного суммирования. В качестве примера приведено новое точное решение, представляющее собой сумму двух решений Громеки–Бельтрами с непараллельными и непересекающимися осями симметрии и одного «сдвинутого и повернутого» ABC -решения. Методом Тркала (с помощью формул (20) и (21)) это новое стационарное винтовое решение Эйлера легко пересчитывается в новое нестационарное решение уравнений Навье–Стокса. Это решение не периодично. У него нет оси симметрии, нет плоскости симметрии и нет центра симметрии. То есть представлено решение, обладающее качественно новой и более сложной картиной течения.

Предложенный метод значительно обогащает запас точных решений уравнений Эйлера и точных решений уравнений Навье–Стокса со сложной топологией течения. Кроме того, некоторые новые решения могут использоваться для описания неосесимметричных волн произвольной амплитуды в рамках недиссипативных уравнений магнитной гидродинамики [20].

Такие решения пригодны не только для теоретических исследований, но и для проверки методов численного интегрирования уравнений сплошной среды.

Основная система координат и матрица перехода. Пусть ij , k - базисные векторы системы Oxyz . И пусть эти векторы имеют такую взаимную ориентацию, что выполнено векторное равенство k = [ i х j ]. Эту систему координат будем называть основной системой координат или, для краткости, основной системой. В точке O , которая в основной системе Oxyz имеет координаты ( x о , у о , z 0 ), расположим другую прямоугольную декартову систему координат OxyZ. Оси этой системы координат могут быть не параллельны осям системы Oxyz . Их направления определяются матрицей перехода:

S =

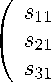
s 12 s 13

s 22 s 23

s 32 s 33

Z4 Z4 Z4

Столбцы матрицы перехода состоят из компонент единичных базисных векторов i , j , k си

Л

)

стемы Ox у) в базисе i,j,k. Например, j = s 12 • i + s 22 • j + s 32 • k. В трехмерном случае семейство таких матриц является трехпараметрическим. С учетом требования k = [i х j, все возможные варианты матрицы S могут быть представлены в виде cos в cos ү cos a sin ү — sin в

sin a sin в cos ү — cos a sin ү cos a sin в cos ү + sin a sin ү \ sin a sin в sin ү + cos a cos ү cos a sin в sin ү — sin a cos ү ,      (П. 1)

sin a cos в                    cos a cos в где a, в, ү — произвольные константы. (Например, s23 = cos a sin в sin ү — sin a cos ү.)

Таким образом, при фиксированной основной системе координат Oxyz , задавая числа x о , У о ,) о и a, в, ү , можно задавать различные системы координат O x у) . Числа x о , у о ,z о определяют положение точки O , а числа a, в, ү — направление осей системы Oxу) .

Любая точка в пространстве имеет координаты как в основной системе Oxyz, так и в системе Oxу). Эти координаты связаны между собой через транспонированную матрицу перехода:

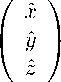
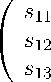
s 21

s 22

s 23

s 31

s 32

s 33

x — x о

у ^— у о

(П . 2)

) — ) о

Перечисленные выше сведения из аналитической геометрии позволяют представлять «сдвинутые и повернутые» известные решения уравнений Эйлера в основной системе ко- ординат.

ABC -решение. Представим «сдвинутое и повернутое» ABC -решение в системе координат Oxyz. Пусть A, B, C, k – произвольные скалярные константы. Согласно (8), скорость V = n i + vj + w k будет скоростью ABC-решения в системе Ox у), если представить n , v, w в виде n = A sin( kz) + C cos( ку), v = B sin(kx) + A cos(kz), w = C sin(ку) + B cos(kx).

Вектор скорости этого ABC -решения V = базисные векторы ij , k , то есть может быть

ZK            ZK               Z4

й i + v j + г) k может быть представлен через w

представлен в виде: V = u i + v j + w k , где

u \ ( s ii s 12 s із \ ( A ^sm( kz) + C cos( ky ) v = s 21 s 22 s 23 B ^sm( kx ) + A cos( kz) w J \s 3i s 32 s 33 / \ C sin( ky ) + B cos( kx )

(П • 3)

Последовательное применение формул (П.2) и (П.3) позволяет представить компоненты u,v,w соленоидальной винтовой скорости в базисе i,j,k через координаты x,y,z. Это скорость «сдвинутого» и «повернутого» ABC -решения. Задавая различное расположение системы координат O xyz, можно получать различные «сдвинутые» и «повернутые» ABC -решения. Хотя по своей физической сущности эти решения являются ABC -решениями, их в общем случае невозможно представить в системе координат Oxyz в «классическом» виде (8). Например, для случая а = 0, в = 0, ү = п/3, x о = у о = z о = 0 матрица S будет иметь вид

/  1/2   -Va/2  о

S =   V3/2   1/2   0

\   0       01

а компонента скорости и , при значении k = 1, вычисленная по формуле (П.3), будет равна: и = 0 . 5 A sln( z ) + C cos( xV 3/2 — у /2) — V 3 B sln( x /2 + у ^/2) — V 3 A cos( z )] . Эта компонента u зависит от координаты x , что невозможно для «классического» ABC -решения.

Решение Громеки–Бельтрами. Получим выражения компонент скорости решения Громеки–Бельтрами в основной системе координат Oxyz . Чтобы отличать эти выражения от полученных выше выражений компонент скорости для ABC -решения, будем использовать обозначения со штрихом. (Это значит, в частности, что используемые ниже обозначения, подобные V ' , не являются обозначением производной.) Чтобы задать решение Громеки–Бельтрами, во-первых, нужно выбрать положение цилиндрической системы координат Ө ' r ' ^ ' X , которое определяется положением точки Ө ' и единичным вектором e х , направленным вдоль оси Ө ' х ' • Это можно сделать, задав координаты x 0 , у 0 , z 0 точки Ө ' в системе координат Oxyz и задав компоненты d i , d 2 , d 3 единичного вектора e х ' = d ' i • i + d 2 • j + d 3 • k в базисе i , j , k основной системы координат. Во-вторых, нужно выбрать функцию тока ^ ' = ^ ' ( г, х ) одного из решений Громеки-Бельтрами. То есть выбрать некоторую линейную комбинацию функций вида (13), соответствующую некоторому выбранному числу k = 0.

Пусть числа x 0 , у ' , z 0 , d i , d 2 , d 3 и функция тока ^ ' = ^ ' ( г, х ), соответствующая числу k = 0, выбраны. Рассмотрим вспомогательную прямоугольную декартову систему координат O ' х ' у ' z ' , у которой начало O ' совпадает с началом Ө ' системы Ө ' г ' ^ ' х ' , а ось O ' z ' совпадает с осью Ө ' X • Очевидно, что эти условия однозначно определяют положение оси O ' z ' , но положения осей O ' х ' и O 'у)' определяются этими условиями с точностью до поворота вокруг оси O ' z ' . Эта неоднозначность выражается в том, что условию совпадения осей (O ' z ' и Ө ' х ' соответствуют различные матрицы перехода от базиса i , j , k системы Oxyz к базису i ' , j ' , k ' системы O ' х ' у ' ) ' :

s ' ii s ' i2 s ' i3

S ' = I s ' 2i s ' 22 s ' 23

s ' 3i s ' 32 s ' 33

Действительно, представим эту матрицу перехода S' в виде (П.1), но вместо символов а, в, Y для обозначения констант будем использовать символы а', в', Ү'. Условие совпадения осей O'z' и Ө'х' означает равенство k' = eх = d'i • i + d2 • j + d3 • k, которое (согласно определению матрицы перехода) однозначно определяет только коэффициенты третьего

столбца матрицы S ' :

cos a sin в ' cos ү ' + sin a ' sin ү ' = d 1 , < cos a sin в ' sin ү ' — sin a cos ү ' = d ' 2 , cos a cos в ' = d 3 •

Поскольку eу = d'i • i + d2 • j + d3 • k - единичный вектор (то есть (d'1)2 + (d2)2 + (d3)2 = 1), то эта система из трех уравнений имеет бесконечное количество решений. Различным ре-

шениям будут соответствовать, вообще говоря, различные положения осей Ox ' и O ' y ' при

А/ М Г                           « заданном положении оси O ж'. Выберем одно из этих решений:

d з >  0;

d з <  0;

' = J — arcsin( d ₂ ) ,

( п + arcsin( d 2 ), в' =

arcsin( d 1 / V 1 — d 22 ) , — arcsin( d 1 / V 1 — d ' 22 ) ,

0 ,

d з >  0 ,  d 22 = 1;

d з <  0 ,  d 22 = 1;

d 22 = 1;

(П • 4)

ү ' = 0 •

Соответствующая этому набору констант a ' , в ' , ү ' матрица перехода имеет вид

S ' =

S11  S12  S із s' 21  s 22 s 23

s ' 31    s ' 32    s ' 33

cos в ' 0 — sin в '

sin a sin в ' cos a sin a cos в '

cos a sin в ' — sin a cos a cos в '

(П • 5)

Транспонированная матрица перехода S ' T позволяет вычислить координаты любой точки в системе O ' x ' y ' z ' через координаты этой же точки в основной системе Oxyz :

x А     / s 11 s 21 s 31 \ ( x — x ' 0

У ' I = I S 12 S 22 S 32 II y — y ' 0

(П • 6)

z '           S 13 s 23 s 33 Z — z ' 0

Теперь запишем выражения для компонент скорости одного из решений Громеки-Бельтрами в системе координат O ' j ' y ' z ' . Пусть функции V ' = V _r' ( r, х ), V ^p = V p ( r, X ), V X = V X ( r, X ) получены по формулам (10) - (12) для выбранной функции тока ф ' = ф ' ( г, х ) и выбранного числа к = 0. Тогда скорость V ' = V ' ( г ' , х ' ) e r ' + Үф ( г ' ,х ' ) e p ' + V X ( r ' ,x ' ) e у будет скоростью одного из решений Громеки–Бельтрами.

Если выбрано решение Громеки–Бельтрами, не имеющее особенностей на оси симметрии, то скорость V ' = V' e r ' + V ^, e ^i + Ү. ^ . e у ' в базисе i ' , j ' , k ' записывается в виде: V ' = u ' i ' + v ' j ' + W3 ' k ' . При этом функции u ' , v ' , w ' вычисляются через координаты ж ' , yj ' , z '

следующим образом. Сначала вычисляются координаты г ' и х ' :

r ' = V x ' ² + y ' ² , х = z ' •

(П • 7)

(П • 8)

Затем функции u ' , v ' , w ' вычисляются по формуле

( x ' V ' r ( г ' ,х ' ) — y ' V Р ( г ' ,х ' ))/ r' \

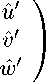
( y ' V ' r ( r ' ,х )+ x ' V ' p ( г ' ,х ' ))/ r '       , r ' = 0;

V ' х ( г ' ,х ' )              /

0            ,            r ' = 0 •

\ V ' х (0 ,х ) /

Наконец, вектор скорости V ' = V ' e г + V ^ e ^ + V^ e у

Z\                zs                   zs

= й ' i ' + v ' j ' + wo ' k ' может быть

представлен в базисе i , j , k в виде: V = й ' i + V j + w ' k , где

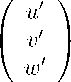
s 11  s 12  s 13 \  / s21   s'22   s'23  I  I

(П • 9)

S 31  s' 32  s' 33

Последовательное применение формул (П.4) – (П.9) позволяет представить компоненты й',v' ,w соленоидальной винтовой скорости решения Громеки-Бельтрами в базисе i, j, k через координаты x, y, z.

Интересно отметить одно свойство формул (П.4) – (П.9). Как сказано выше, выбор констант а', в ' , ү ' , обеспечивающий совпадение осей O ' ) ' и Ө ' X , неоднозначен. Формулы (П.4) дают лишь один из возможных вариантов. При другом выборе констант а ' , в ' , Ү ' , обеспечивающим совпадение осей O ' ) ' и Ө ' X , матрица перехода (П.5), вообще говоря, изменится. Но окончательный результат последовательного применения формул (П.5) – (П.9) не изменится. Без доказательства заметим, что это свойство следует из наличия осевой симметрии у решения Громеки–Бельтрами.

Геометрический смысл констант α, β, γ . Иногда ориентацию осей прямоугольной декартовой системы координат OXу) относительно основной системы Oxy) удобно задавать как результат последовательного выполнения некоторых поворотов. В этом случае для вычисления матрицы перехода полезно использовать геометрический смысл констант α, β, γ , которые являются углами некоторых поворотов. Матрица перехода не зависит от положения точки O . Поэтому, для простоты, рассмотрим случай O = O и покажем, какие именно повороты приводят к системе O)у) .

Первый поворот – это поворот системы Oxyz вокруг оси Oz на угол γ . При этом положительным считается угол такого поворота, при котором винт с правой резьбой продвигается в положительном направлении оси Oz . В результате получается промежуточная система Ox 1 y 1 z 1 .

Второй поворот – это поворот промежуточной системы Ox 1 y 1 z 1 вокруг (новой) оси Oy 1 на угол β . При этом положительным считается угол такого поворота, при котором винт с правой резьбой продвигается в положительном направлении оси Oy 1 . В результате получается вторая промежуточная система Ox 2 y 2 z 2 .

И, наконец, третий поворот – это поворот второй промежуточной системы Ox 2 y 2 z 2 вокруг оси Ox 2 на угол α . При этом положительным считается угол такого поворота, при котором винт с правой резьбой продвигается в положительном направлении оси Ox 2 .

В результате получается система O)у). При использовании этого геометрического свойства констант α, β , γ следует иметь в виду, что в общем случае приведенный выше порядок выполнения поворотов имеет существенное значение.

• 8.    Приложение 2. Примеры представления точных решений в прямоугольной декартовой системе координат

В пятом разделе данной работы предложено просуммировать скорости трех винтовых решений. Получим выражения компонент скорости для каждого из этих решений в системе Oxyz по отдельности.

Первое решение. Для получения выражений компонент скорости первого решения воспользуемся обозначениями Приложения 1. Согласно описанию первого решения, начало цилиндрической системы координат Ө'r'XX совпадает с началом системы Oxy). То есть все три числа )0, у0, )0, определяющие положение точки Ө', равны нулю. Если использовать обозначения Приложения 1, то условие eX> = 0 • i+0 • j + 1 • k, задающее направление оси Ө'х', означает, что d1 = 0, d2 = 0, d'3 = 1. Отсюда по формулам (П.4) получаем а' = в' = Y' = 0, и формула (П.5) дает следующую матрицу перехода:

/ sii  s 12  sіз         i   оо \

S' =   s 21 s 22 s 23   =   0 10

(П . 10)

\ s31  s32  s'33         0  01 /

Для первого решения выбрана функция тока X = X ( r ' ,X ) = r ' J 1 (Va r ' ) sin( X )• Она задает скорость V ' = V ' ( r ' , X ) e r ' + V / ( r ' ,X ) ^e ^ ' + V X ( r ' ,X ) ^e x ' винтового решения, где функции V' = V' ( r,X ), V = V( r ' ,X ), V X = V X ( r,X ) вычисляются по формулам (14). Например: V /( r ,X ) = — 2 J 1 ( V a r ' ) sin( X )• Последовательное применение формул (П.10), (П.6), (П.7), (14), (П.8), (П.9) позволяет представить столбец компонент скорости решения Громеки – Бельтрами, в системе координат Oxyz :

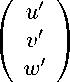
( xJ 1 ( V a r ' ) ( yJ 1 ( V a r ' )

Формула (П.11) позволяет

cos (z) +2yJ1(Var') sin(z))/r' \ cos (z) — 2xJ1(Var') sin(z))/r'     , r' = Vx2 + у2 = 0;

— V J o ( V 3 r ' ) sin( z )

/       0       \

0          ,                   V x ² + у ² = 0 .

—V a sin( z )

(П. 11) вычислить компоненты u',v',w' скорости первого решения через переменные x, y, z.

Второе решение. Этому решению соответствует другая цилиндрическая система координат Ө"r''X'X'• Далее все обозначения с двумя штрихами будут иметь тот же смысл, какой имеют эти же обозначения с одним штрихом в Приложении 1. По условию, точка Ө'' в системе Oxyz имеет координаты x0 = 2, у0 = 0, z0' = 0, а положительное направление оси Ө'X'' задается единичным вектором eу = 1 / Va • i + 1 / Va • j + 1 / Va • k. Поэтому d' = 1 / Va, d2 = 1 / Va, d3 = 1 / Va.

Отсюда по формулам (П.4) получаем а " = — arcsin(1 /W ,

(П.5) дает следующую матрицу перехода:

в ' = п /4 , ү '' = 0, и формула

( s' 11  s' 12  s' 13         1/V2   — 1/Ve  1/Va\ s'' = I s'21  s'22  s'23  I = I 0     V2/Va  1/Va s'31 s'32 s'33        — 1/V2  — 1/V61

Для второго решения выбрана функция тока X ' = X ' ( r '' ,X ' ) = r '' J i (V5 r '' ) exp( — X ' ). Соответствующие ей функции V _r'' = V _r'' ( r " ,Х ' ), V/ ' = V/ ' ( r ' ,Х ' ), V X ' = V X c ( r ' ,X. ' ) вычисляются по формулам (15). Матрица перехода S ' не так проста, как матрица (П.10). Поэтому столбец компонент скорости выбранного решения Громеки–Бельтрами в системе координат Oxyz удобнее представить не в виде одной громоздкой формулы, а как результат последовательного применения нескольких формул:

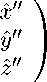
/ 1/V2     0     — 1/V2 \ / x — 2 \

(П . 12)

(П . 1a)

— 1 / ^V 6 ^V 2 / ^V a — 1 / ^V 6        у ,

\ 1/Va 1/Va   1/Va        z r" = Vx''2 + H''2, X' = z'',

( —x"J 1 ( V 5 r" ) exp( -X' ) + 2 у " J 1 ( V 5 r" ) exp( —X' ) )/ ^r" \

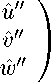
( — y '' J 1 ( V 5 r '' ) exp( -X ' ) — 2 x '' J 1 ( V5r '' ) exp( — X ' ) )/ r '' I , r" = 0;

-v 5 J o ( V 5 r '' ) exp( —X ' )

/        0

0                ,               r '' = 0 .

\ ^—V 5 exp^{( —}x " ) )

(П . 14)

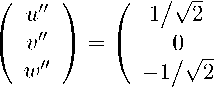
—1/V6  i/Va \ / u''\

(П . 15)

V2 / Va  1/Va       v''

—1/V6  1/Va ) \ w'')

Последовательное применение формул (П.12) – (П.15) позволяет вычислить компоненты u '' , v '' , w " скорости второго решения через переменные x, y, z .

Третье решение. Согласно описанию третьего решения, оси системы Oˆxˆyˆzˆ получаются вращением осей системы Oxyz вокруг оси Oy на угол π/4 в направлении, показанном на рис. 3. Воспользуемся геометрическим смыслом констант α, β, γ, описанным в конце Приложения 1. Учитывая правило для определения положительного направления поворота, получаем, что системе Oˆ xˆyˆ zˆ соответствует последовательность поворотов с углами ү = 0, в = —п/4, а = 0. Поэтому матрица перехода, вычисленная по формуле (П.1), имеет вид

S =

1  20

\ 1/ V 2 0

— 1/V2

1 / ^V 2

Точка O задается координатами x 0 =3 , третьего решения имеет вид

/ x \    / 1 / V 2

y ˆ   =      0

\ z /    \ — 1 / V 2

y 0 =3 ,z 0 =0. Поэтому формула (П.2) для

0 1 / V 2 \ / x — a \

1     0 y — a .                     ( п . 16)

0 1 / V 2        z

В системе координат Ox ˆ y ˆ z ˆ третье решение является «классическим» ABC -решением с параметрами A =1 , B =2 , C =3 ,k =2. Поэтому формула (П.3) имеет вид

/ u \    / 1/V2 0 — 1/V2 \ / sin(2 z ) + acos(2 У ) \

(П . 17)

v =     01    0         2 sin(2 x ˆ) + cos(2 z ˆ)     .

у w /     \ 1 / V 2 0  1 / V 2 У \ asin(2 y )+2cos(2 x ) У

Таким образом, компоненты скорости третьего решения в системе координат Oxyz вычисляются через переменные x, y, z в результате последовательного применения формул (П.16) и (П.17).