Полуэмпирическое уравнение вязкости трехкомпонентных неорганических стекол

Автор: Машанов Алексей Алексеевич, Мантатов Владимир Владимирович, Сандитов Дамба Сангадиевич

Журнал: Вестник Бурятского государственного университета. Химия. Физика @vestnik-bsu-chemistry-physics

Статья в выпуске: 1, 2016 года.

Бесплатный доступ

Рассмотрено применение нового уравнения к температурной зависимости вязкости трехкомпонентных стекол GeO2 - Na2O - PbO, GeO2 - Na2O - BeO, B2O3 - CaO - Al2O3, B2O3 - PbO - Al2O3. Уравнение находится в удовлетворительном согласии с экспериментальными данными, за редкими исключениями. По полученным значениям эмпирических постоянных рассчитана энергия делокализации атома и потенциал перескока кинетической единицы в новое положение.

Силикатные стекла, делокализация мостикового атома, вязкое течение, свободная энергия активации текучести

Короткий адрес: https://sciup.org/148316648

IDR: 148316648

Текст научной статьи Полуэмпирическое уравнение вязкости трехкомпонентных неорганических стекол

Недавно предложено трехпараметрическое уравнение вязкого течения стеклообразующих расплавов [1], которое можно записать в виде:

П = A exp s--+ exp где А, B и C – эмпирические постоянные. Было показано, что уравнение находится в удовлетворительном согласии с экспериментальными данными ряда двухкомпонентных (в основном, щелочносиликатных) стекол в широком интервале температур.

Настоящее сообщение посвящено применению данного соотношения к трехкомпонентным германатным и боратным стеклам.

Кратко о выводе формулы (1). Предполагается, что вероятность перехода кинетической единицы W из одного равновесного положения в другое определяется, во-первых, вероятностью локального изменения структуры W 1 у данной кинетической единицы и, во-вторых, вероятностью W 2 того, что она обладает достаточной энергией Δ F ∞ для перескока в новое положение

W = W 1 W 2

При повышенных температурах в аморфных системах всегда имеются «разрыхленные микрообласти» и поэтому нет надобности в локальном изменении структуры: W 1 = 1. В данной области молекулярная подвижность определяется вероятностью перескока кинетической единицы в одну из этих «готовых» микрообластей W 2 .

С понижением температуры, в области стеклования, структура расплава упорядочивается, уплотняется и в подвижности молекул существенную роль начинает играть вероятность локального изменения структуры W 1 , которую в рамках модели делокализованных атомов [2, 3] можно выразить с помощью определенной формулы в виде “двойной экспоненты” [1].

Полагаем, что делокализация активного атома – его смещение из равновесного положения – сопровождается перемещениями соседних частиц и отражает локальное конфигурационное изменение структуры в аморфных веществах.

Используя известную связь между вязкостью η и величиной W в соответствии с теорией Стокса-Эйнштейна, а также соответствующие соотношения для W 1 и W 2 , приходим к уравнению вязкости [1]

Гаf Г f ае ) ,11

П = n n exp 1--- + exp ---- - 1 г

0 I kT I kT J I ,

которое можно представить в виде эмпирического выражения (1). Здесь Δ F ∞ – потенциал перескока атома, Δε e – энергия делокализации атома.

Постоянные A , B и C в соотношении (1) имеют следующий физический смысл ( R – газовая постоянная)

B = Δ F ∞ /R, C = ∆ε е /R, A = η 0 , коэффициент пропорциональности А равен предельной вязкости η 0 при T → ∞.

Сравнение с экспериментом и обсуждение результатов. В уравнение (1) входят три параметра A, B и C. Предэкспоненциальный множитель А, соответствующий предельной вязкости η0 при повышенных температурах, находится путем экстраполяции (с помощью полинома Лагранжа) кривой вязкости lgη – 1/T к температуре T → ∞ (рис. 1) [4]. Зная А, за счет подгонки оставшихся двух параметров В и С по уравнению (1) можно рассчитать вязкость.

В качестве объектов исследования выбрали трехкомпонентные германатные и боратные стекла (табл. 1). На графиках в координатах lg η – 1/ T точки соответствуют экспериментальным данным [5], а кривые – расчету по уравнению (1). Как видно, расчетная кривая ложится на экспериментальные точки (рис. 1 и 2). В табл. 1 приводятся значения параметров A , B и C , при которых расчет согласуется с экспериментом. Однако надо отметить, что у ряда боратных стекол наблюдается отклонение от уравнения (1). В качестве примеров в табл. 2 приводится сравнение рассчитанных (lg η расч. ) и экспериментальных (lg η экс. ) значений вязкости для некоторых стекол. Согласие между расчетом и экспериментом, можно считать удовлетворительным. Отклонение расчета от опыта в среднем составляет около 2–3%, хотя в отдельных случаях (для боратных стекол) достигает 6– 8%.

По данным об эмпирических постоянных В и С были рассчитаны энергетические параметры уравнения (2) Δ F ∞ и Δ ε e . Обращает внимание относительное постоянство энергии делокализации атома Δ ε e у стекол одного класса. Например, у германатных стекол она составляет Δ ε e = 23-28 кДж/моль, а у боратных систем B 2 O 3 – CaO – Al 2 O 3 – равна Δ ε e ≈ 31-33 кДж/моль (табл. 1).

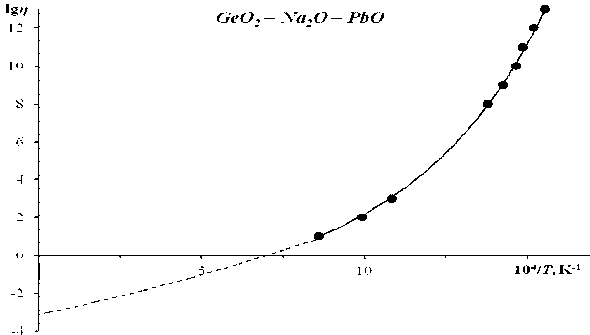
Рис. 1. Температурная зависимость вязкости стекла GeO 2 – Na 2 O – PbO в координатах lg η – 1/ T . Вязкость дана в пуазах (П).

Точки – экспериментальные данные, кривая – расчет по уравнению (1), пунктирная кривая – экстраполяция с помощью полинома Лагранжа. Содержание окислов, мол.%: GeO 2 – 52.39, Na 2 O – 10.35, PbO – 37.26. Параметры уравнения (1): lg( А , П) = - 3.12, В = 6375 К , С = 2766 К .

Ранее было развито представление о том, что процессу «делокализация атома» в неорганических стеклах и их расплавах соответствует некоторое критическое смещение мостикового атома (типа атома кислорода в мостике Si – O – Si ), связанное с локальной низкоактивационной вязкоупругой деформацией сетки валентных связей. Например, у силикатных стекол величина Δ ε e равна около 20 кДж/моль и характеризует работу, необходимую для смещения мостикового атома кислорода в мостике Si – O – Si [3]. По-видимому, энергия делокализации атома Δ ε e ≈ 25-30 кДж/моль (табл. 1) у исследованных нами оксидных неорганических стекол связана с работой смещения мостикового атома кислорода в мостиках Ge – O – Ge и B – O – B .

Потенциал перескока атома Δ F ∞ ≈ 30-40 кДж/моль (табл. 1) у трехкомпонентных германатных и боратных стекол оказывается примерно в два раза меньше, чем у двухкомпонентных щелочносиликатных стекол Δ F ∞ ≈ 100 кДж/моль [1].

Таблица 1

Параметры уравнений (1) и (2) для трехкомпонентных германатных и боратных стекол. Использованы данные [5]

Содержание окислов,			lg ( A , П)	В С		Δ F ∞ 1 Δ ε e
	мол.%		lg ( A , П)	К		кДж/моль
GeO 2	Na 2 O	PbO		GeO 2	– Na 2 O –	PbO
67.84	11.48	20.68	-2,67	3608	3007	30	25
60.54	17.93	21.53	-3,12	5894	2826	49	23
52.39	10.35	37.26	-3,12	6375	2766	53	23
GeO 2	Na 2 O	BeO		GeO 2	– Na 2 O –	BeO
83.1	14.67	2.84	-2,49	4811	3368	40	28
74.85	22.17	2.98	-2,20	3608	3247	30	27
78.3	15.46	6.24	-2,11	4811	3368	40	28
B 2 O 3	CaO	Al 2 O 3		B 2 O 3	– CaO – Al 2 O 3
54.38	23.89	21.72	-2,83	4811	3729	40	31
57.83	17.47	24.7	-2,60	4450	3608	37	30
59.73	22.05	18.22	-3,06	4330	3849	36	32
60.72	24.46	14.82	-3,71	4330	3969	36	33
69.48	15.99	14.54	-2,88	4811	3729	40	31
B 2 O 3	PbO	Al 2 O 3		B 2 O 3	– PbO – Al 2 O 3
75.4	23.6	1	-4,87	14674	1924	120	16
75.55	22.46	1.99	-2,98	5172	3007	43	25
76.32	20.14	3.54	-2,13	4210	3007	35	25

Таблица 2

Сравнение расчета по уравнению (1) с экспериментальными данными трехкомпонентных стеклообразующих расплавов

GeO 2 – Na 2 O – PbO			B 2 O 3 – CaO – Al 2 O 3			SiO 2 – CaO – Al 2 O 3
GeO 2 1 Na 2 O		PbO	B 2 O 3	CaO Al 2 O 3		SiO 2	CaO	Al 2 O 3
Содержание окислов, мол.%
67.84	11.48	20.68	69.48	15.99	14.54	47.98	38.34	13.68
Сравнение lg η расч и lg η экс
T , ⁰C	lg η экс	lg η расч	T , ⁰C	lg η экс	lg η расч	T , ⁰C	lg η экс	lg η расч
904	1	0,72	1126	1	0,91	1261	0,98	1,08
737	2	2,02	955	2	2,15	1237	1,14	1,28
656	3	3,08	867	3	3,16	1213	1,31	1,50
598	4	4,17	808	4	4,08	1188	1,51	1,74
478	8	8,17	672	8	7,59	1164	1,75	1,99
453	9	9,54	645	9	8,67	859,6	8,14	7,95
439	10	10,44	620	10	9,86	839,3	8,85	8,68
427	11	11,29	598	11	11,07	822,9	9,53	9.34
413	12	12,41	578	12	12,35	792,9	10,7	10,65
401	13	13,49	557	13	13,91	779,7	11,44	11,30

Примечание: Вязкость дана в пуазах (П). Использованы данные [5].

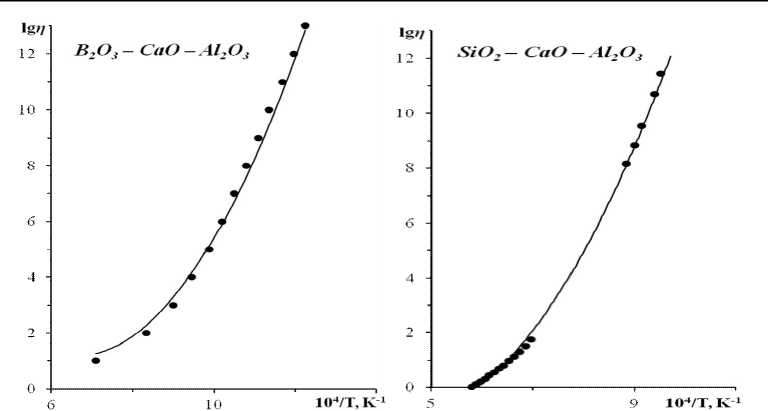
Рис. 2. Температурная зависимость вязкости стекол SiO 2 – CaO – Al 2 O 3 (а) и B 2 O 3 – Na 2 O – Al 2 O 3 (b). Точки – экспериментальные данные, кривая – расчет по уравнению (1).

Заключение

Новое уравнение вязкости [1] находится в удовлетворительном согласии с данными для трехкомпонентных германатных и боратных стекол. Оно лучше выполняется для германатных стекол (с преимущественно сеточной структурой), чем у боратных стекол (с линейной и линейно-разветвленной структурой).

Список литературы Полуэмпирическое уравнение вязкости трехкомпонентных неорганических стекол

Сандитов Д. С., Мункуева С. Б., Сангадиев С. Ш. Конфигурационно- активационная теория вязкого течения сильновязких жидкостей // Вестник Бурятского госуниверситета. Химия. Физика. - 2016. - Вып. 3. - С. 112-119.
Сандитов Д. С. Модель делокализованных атомов в физике стеклообразного состояния // ЖЭТФ. - 2012. - Т. 142, Вып.1 (7). - С. 123- 137.
Сандитов Д. С., Бадмаев С. С. О делокализации атома в стеклах и их расплавах // Физика и химия стекла. - 2015. - Т.40, № 5. - С. 612-630.
Сандитов Д. С., Машанов А. А. Математическая обработка экспериментальных данных о вязкости расплавов стекол в широком интервале температур // Физика и химия стекла. - 2010. - Т. 36, № 1. - С. 55- 59.
5MDL® SciGlass-7.8. - Institute of Theoretical Chemistry, MA: Shrewsbury, 2012. - www.sciglass.info.

Статья научная