Polyphase Structure Based Eigen Design of Two-Channel Quadrature Mirror Filter Bank
Автор: S. K. Agrawal, O. P. Sahu
Журнал: International Journal of Image, Graphics and Signal Processing(IJIGSP) @ijigsp
Статья в выпуске: 10 vol.6, 2014 года.
Бесплатный доступ
This paper presents a method for the design of two-channel quadrature mirror filter (QMF) banks with linear phase in frequency domain. Low-pass prototype filter of the QMF bank is implemented using polyphase decomposition. Prototype filter coefficients are optimized to minimize an objective function using eigenvalue-eigenvector approach without matrix inversion. The objective function is formulated as a weighted sum of four terms, pass-band error and stop-band residual energy of low-pass analysis filter, the square error of the overall transfer function at the quadrature frequency and amplitude distortion of the filter bank. The simulation results clearly show that the proposed method requires less computational efforts in comparison to the other state-of-art existing design methods.
Nonlinear optimization, Polyphase decomposition, Sub-band coding, Perfect reconstruction
Короткий адрес: https://sciup.org/15013437
IDR: 15013437
Текст научной статьи Polyphase Structure Based Eigen Design of Two-Channel Quadrature Mirror Filter Bank
Published Online September 2014 in MECS
Quadrature mirror filters (QMF) are based on the concept of splitting the bandwidth of the original spectrum in two halves, the low and the high bands. This is done by designing special purpose low-pass and high-pass filters [1]. Two-channel QMF bank finds applications in various signal processing fields, such as multicarrier modulation systems [2], design of wavelet bases [3], image coding [4], digital trans-multiplexers [5], discrete multi-tone modulation systems [6], ECG signal compression [7], antenna systems [8], speech compression [9], biomedical signal processing [10] and acoustic echo-cancellation [11].
Various unconstrained and constrained optimization techniques [12—25] have been developed for the design of two-channel QMF banks in both time and frequency domains. Analysis and synthesis sections of a typical QMF bank are shown in Fig. 1. Using the low-pass and high-pass analysis filters H 1 ( z ) and H 2 ( z ), an input signal x ( n ) is divided into two equally spaced frequency subbands. These sub-band signals are decimated by a factor of 2 to accomplish signal compression. At the receiver end, sub-band signals are interpolated and recombined using similar set of synthesis filters to obtain the reconstructed output signal. Due to the fact that filters H 1
( z ), H 2 ( z ), G 1 ( z ), and G 2 ( z ) are not ideal, the output signal y ( n ) suffers from three errors: aliasing distortion (ALD), phase distortion (PHD) and amplitude distortion (AMD) [26, 27]. Thus, the design problem for the two-channel QMF bank is to find the optimal filters for the analysis/synthesis sections such that the reconstructed signal y ( n ) approximates the original signal x ( n ).
The expression for the overall transfer function of the alias free two-channel QMF bank can be written as [16-23]
T (z)= ^H^z)-H2(-))]
where synthesis filters are defined in terms of analysis filters as given below for alias cancellation
Gi ()) = H2(-)) and G2()) = -H(-)),(2)
and mirror image analysis filters H 1 ( z ) and H 2 ( z ) are related to each other by following equation
H ()) = Hi(-))
Equation (1) indicates that the overall design task reduces to the determination of the optimized filter coefficients of the low pass analysis filter H 1 ( z ) only, which is known as low-pass prototype filter. To obtain the exact reconstruction QMF bank, PHD and AMD should also be eliminated, in this case the overall transfer function T ( z ) must be a pure delay, i. e.,
T (z) = c) ""n ° (4)
Let the low-pass filter H 1 ( z ) is selected to be a linearphase finite impulse response (FIR) with even filter length N , then from (1), T ( z ) also becomes linear phase FIR and PHD of QMF bank is eliminated completely. The inverse Z transform h 1 ( n ) of H 1 ( z ) is given by
Mn) = ^(W-1-n) (5)
The corresponding frequency response has the form
H (e J'“ ) =e-jM(N" i)/2 HR(w) (6)
where H R ( ω ) is the amplitude function. For real impulse response h 1 ( n ), the magnitude response | H 1 ( ejω ) | is an even function of ω , therefore, by substituting (6) into (1)
yields the overall frequency response of QMF bank as follows:
Prototype low-pass filter
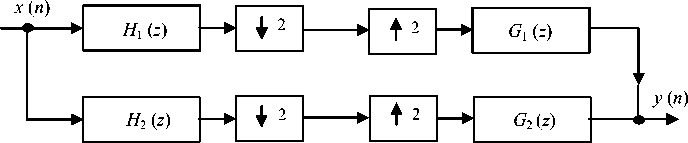
Analysis Bank-
Synthesis Bank-
Fig. 1. Two-band QMF bank
Т (e] " )
(е - jaQV- 1) )
= 1—_—^[|H i (e] « )|2(-i)a v - Цщ^ е^ - " )р]
If filter length ( N ) is selected to be odd, then the above equation gives severe amplitude distortion at quadrature frequency. Therefore, N must be chosen to be even and the condition for exact reconstruction (ER) can be written [1]
| Т^ “ )| = |771(е]й,)|2 + |772(е] " )|2 = с, for all го . (8)
After eliminating ALD and PHD completely, we can only minimize amplitude distortion [26] rather than completely eliminated due to mirror image symmetry constraint of (3). If the characteristics of prototype filter are assumed ideal in pass-band and stop-band regions then |T ( ejω ) | will be constant in the pass bands of H 1 ( z ) and H 2 ( z ) and ER condition is automatically satisfied in these regions. The main hurdle comes in transition band region. Thus, the aim is to find the optimal coefficients for the FIR low-pass prototype filter such that the flat exact reconstruction condition must be satisfied given in (8).
This paper proposes an improved technique for the design of QMF bank by representing the low-pass prototype filter using polyphase structure and minimization of a quadratic error function by unconstrained iterative method without any matrix inversion. In section 2, polyphase representation and formulation of design problem are discussed. Section 3 presents the design algorithm. Section 4 describes the simulation results with design examples. Finally, conclusions are drawn in section 5.
-
II. Polyphase Representation Of Qmf Bank
The polyphase decomposition can be used to implement the analysis and synthesis sections of a filter bank in a very computationally efficient manner [1, 26]. In general, M-fold decimation filter or interpolation filter can be implemented with approximately M-fold reduction in the number of multiplications per unit time (MPUs) and number of additions per unit time (APUs) by using the polyphase representation. Polyphase component based complete two-channel QMF bank requires only about (N-1)/2 MPUs and (N-1)/2 APUs [1], where N is the filter length of H1 (z). Type1 polyphase representation [1] of analysis filters is given by
771 Ю = E((z 2)+ z"1 Е( (z2 )
Н2(z) = E((z2)- z -1 E^z2)
Where
Ei(z) = Mh(2n)z-n and E((z) = '^^(2n +1)z-n n=0
where M = ( N —2)/2
then, E 2 ( z ) can be expressed as
E2 (z) = z-cv-2) / 2E1(z- ^ (13)
By using the above concept, the polyphase structure for two-channel QMF bank with noble identities described in [26] can be modified as depicted in Fig. 2.
By substituting E 2 (z ) from (13) into (9), we obtain
H1 (z) = E((z2 )+ z “ 1.z_(w-2)£'1(z_ 2) (14)
The frequency response of prototype filter is given by
Нг (e1 " ) = E((e2i“) + e"j^N1 ^Ede"2^ (15)
Where
( N - 2)/2
E ( ( ) Y e ( n)e j (16)
n = 0

-Analysis Bank-
Synthesis Bank-
Fig. 2. Complete two-band QMF bank using proposed polyphase form
( N - 2)/2
H ( (e1 “ ) = £ e ( n ) [ e ™ + e j ( N - 1) e 2 ™ ] (17)
n = 0
Comparing (17) with (6) yields
Hr (to) =
( N - 2)/2 /
Eb cos ™ 2n -n n=0 V
( N - 1) )
2 )
bTc (to)
c (<*>) =
[costo (o - (^" 1)) c OSto (2 - (^" 1)) - . cOS to (( ^" 1) -
1)]T (20)
A. The Objective Function
The objective function should reflect the stop-band energy as well as the accuracy of pass-band and transition band. In this paper, the QMF design problem is formulated as a multi-objective unconstrained optimization problem. A novel objective function is formulated as a weighted sum of four terms:
E = a(Ep + a2E+ + a3 E+ + a4. Em (21)
where α 1, α 2 , α 3 and α 4 are real constants, and E p , E s , E t and E m are the pass-band error, stop-band residual energy, square error of the T ( z ) at ω = π /2, and amplitude distortion, respectively. For exact reconstruction, the | T ( ejω ) | must be equal to | H 1 ( ejω ) | 2 at ω = 0. Consequently, at ω = π /2 the exact reconstruction condition of (8) can be expressed as
HR (я/2)= 0.707 HR0O) (22)
where H R ( π /2) and H R (0) are the amplitude responses of prototype filter at ω = 0 and ω = π /2, respectively. Using (19) and (22), the square error E t in transition band can be implemented as
Et = [Hr(я/2)- 0.707 Hr(0)]2(23)
Et = [bTq — 0.707 bTc(0)]2 = [bTq - HR(]2
where vector q is equal to vector c(to), when it is evaluated at ω = π /2, and H R1 = 0.707 bTc(0) .
Similarly, E p and E s can be obtained
™ Pd
Er = J [|Hr (0)1 - Hr (™)|]2 —(25)
= bTF b where F is symmetric and positive definite matrix, given by
™ p
F = f [ c (0) - c ( to ) ][ c (0) - c ( to ) ] T d ™
П
Г । 12 d ™
E, = J H r ( ® )| —
П ms
= bT G b
where G is symmetric and positive definite calculated as
matrix,
=
π ∫ d ω c ( ω ) c ( ω )
π
ω s
E m can be realized as
^т = |Т(ejM)|- to |т(ejM)|
-
III. Optimization Algorithm
Substituting (24), (26), (29) and (31) into (21) yields
E= ат bTFb + a2 bT G b + «3 [bTq - H^ ]2+ a4 ․
= + «3 [-2HRibTq + Hri2]+α4 Em(32)
Where matrix R is
R= + a2 G + «з S and S = qqT
R is a real, symmetric and positive definite matrix and objective function E is in quadratic form. So, the minimization problem can be formulated to calculate optimal b as an eigenvector corresponding to the minimum eigenvalue λ min of R . The standard methods for finding the eigenvalues of a large matrix are not efficient. In this paper a modified Power method without any matrix inversion [1] is used to determine minimum eigenvalue and corresponding eigenvector in the eigenspace for the minimization problem. Power method is an iterative method which starts with an initial arbitrarily chosen vector p 0 and generates a sequence of approximations p k to get optimized filter coefficients corresponding to λ min of R .
A step-by-step algorithm for designing the prototype low-pass filter based on the principle discussed above is as follows:
-
(9) Compute maximum eigenvalue (λmax1) of matrix R from step (7) and define a new matrix A = λmax1.I ─ R, which is positive semi-definite.
-
(10) Again compute the maximum eigenvalue (λmax2) for matrix A using same procedure in step (6) and step (7) for matrix R.
-
(11) Minimum eigenvalue (λmin) for matrix R can be calculated by the relation λmax2 = λmax1─ λmin without involving any matrix inversion.
-
(12) The optimum solution is b = bi+1 and finally compute h1(n).
-
IV. Design Examples and Discussion
In this section, we present MATLAB based computer simulations for QMF bank using the above algorithm. A desktop computer equipped with Intel Core 2 Duo CPU @ 2.10 GHz, 1 GB RAM is used to test the programs. The performance and effectiveness of the algorithm is evaluated in terms seven significant quantities: Peak reconstruction error (PRE) in dB = to |10log| T ( eito )|| - to |10log| T ( eiM )||, Pass band error ( E p ), Stop band error ( E s ), Computational time (CPU time), number of iterations (NOI), stop-band edge attenuation ( A s ) = - 20 log 10 ( H 1 (ω s )) and stop-band first lobe attenuation ( A L ). The constants α 1, α 2 , α 3 and α 4 are selected by trial and error method to find the best possible solution. Table 1 demonstrate the comparison of the proposed method with other state-of-art existing method for filter length ( N ) = 24 in terms of significant quantities with similar design specifications.
-
A. Design Examples
0.013591,
h
1
(12) = - 0.000551,
h
1
(13) = 0.024433,
h
1
(14) = - 0.003557,
h
1
(15) = - 0.041045,
h
1
(16) = 0.013497,
h
1
(17) = 0.066259,
h
1
(18) = - 0.034971,
h
1
(19) = -
0.107700,
h
1
(20) = 0.084400,
h
1
(21) = 0.199042,
h
1
(22) = - 0.261766,
h
1
(23) = - 0.929945.
0.940639.
Example 1 : For N = 48, ω s = 0.6π, ω p = 0.4π, α 1 = 0.95 , α 2 = 0.1, α 3 =0.05 and α 4 = 10-2, the following filter tap weights for the FIR low-pass prototype filter ( H 1 ( z )) yields after 12 iterations:
h 1 (0) = - 0.000030, h 1 (1) = 0.000069, h 1 (2) = 0.000157, h 1 (3) = - 0.000357, h 1 (4) = - 0.000456, h 1 (5) = 0.001185, h 1 (6) = 0.000951, h 1 (7) = - 0.00310119, h 1 (8) = - 0.00151, h 1 (9) = 0.00689464, h 1 (10) = 0.001689, h 1 (11) = -
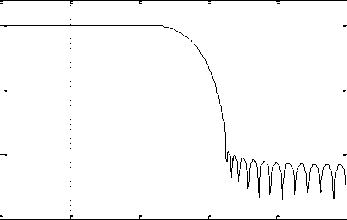
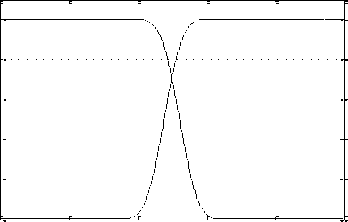
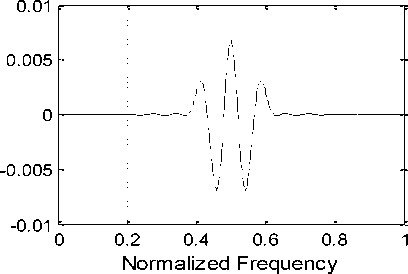
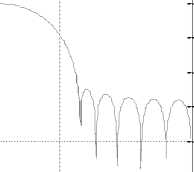
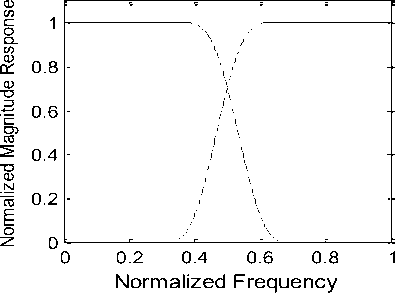
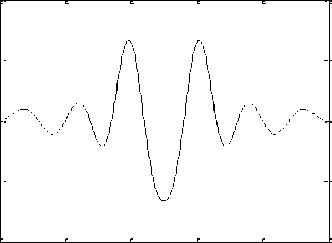
The significant quantities obtained are E p = 2.725×10-11, E s = 7.224×10-12, A s = 67.7 dB, A L = 97.65 dB, CPU-time = 0.0686 sec., and PRE = 0.0068 dB. For example 1, the resulting magnitude response of low-pass prototype filter is shown in Fig. 3a. The normalized magnitude plots of analysis filters H 1 ( z ) and H 2 ( z ) are displayed in Fig. 3b. Figures 3c and 3d depict the reconstruction error (in dB) and overall magnitude response of the QMF bank, respectively.
Example 2: For N = 24, ωs = 0.6π, ωp = 0.4π, α1 = 0.61, α2 = 0.9, α3 = 0.06 and α4 = 10-2, the following filter tap weights for the FIR low-pass prototype filter (H1 (z)) yields after 06 iterations:
h 1 (0) = - 0.002162, h 1 (1) = 0.006417, h 1 (2) = 0.003313, h 1 (3) = - 0.020964, h 1 (4) = -0.000133, h 1 (5) = 0.048519, h 1 (6) = - 0.015659, h 1 (7) = - 0.097246, h 1 (8) = 0.062790, h 1 (9) = 0.198991, h 1 (10) = - 0.243114, h 1 (11) = -
The significant quantities obtained are Ep = 1.9471×10-7, Es= 9.6599×10-7, As = 34.18 dB, AL = 49.96 dB, CPUtime = 0.0288 sec., and PRE = 0.0266 dB. For example 2, the resulting magnitude response of low-pass prototype filter is shown in Fig. 4a. The normalized magnitude plots of analysis filters H1 (z) and H2 (z) are displayed in Fig. 4b. Figures 4c and 4d depict the reconstruction error (in dB) and overall magnitude response of the QMF bank, respectively.
It can be clearly observed from table 1 that the performance of the proposed design technique is better than all other methods in terms of E , A , A , number of s, s, , iteration (NOI) required and the CPU time of the processor. The performance in terms of reconstruction error is also comparable with other existing methods. Consequently, the main advantage of proposed technique is reduction in computational burden and it is suitable for various engineering fields such as image and speech compression.
-50
-100
-150
0 0.2 0.4 0.6 0.8 1
0.8
0.6
0.4
0.2
0 0.2 0.4 0.6 0.8 1
Normalized Frequency (a)
Normalized Frequency (b)
(c)
Fig. 3 (a) Magnitude response of low-pass analysis filter for N = 48 (b) Normalized Magnitude responses of analysis filters H1 (z) and H2 (z) (c) Reconstruction error in dB (d) Overall magnitude response of the QMF bank
1.02

1.01
0.99
0.2 0.4 0.6 0.8
0.98 0
Normalized Frequency (d)
-20
-40
-60
-80
-100
-120
0 0.2 0.4 0.6 0.8
Normalized Frequency (a)
(b)
0.04
CQ
0.02 о ш о 0 Z5 О -0.02 о -0.04 0 0.2 0.4 0.6 0.8 1 Normalized Frequency (c) (d) Fig. 4 (a) Magnitude response of low-pass analysis filter for N =24 (b) Normalized Magnitude responses of analysis filters H1 (z) and H2 (z) (c) Reconstruction error in dB (d) Overall magnitude response of the QMF bank Table 1: Performance comparisons of proposed method with state-of-art existing methods for N = 24 Methods Es Ep PRE (dB) As (dB) AL (dB) NOI CPU time(s) Ghosh et al. [23] 1.30×10-4 9.14×10-7 0.030 20.11 30.93 ----- ------ (MJADE_pBX algorithm) Upendar et al. [19] 7.99×10-5 1.84 ×10-7 0.019 22.78 34.43 122 1.48 PSO [20] 4.69×10-5 1.28 ×10-7 0.017 28.86 38.8 128 1.69 Yue -Dar J. [24] --- --- 0.043 22.05 --- 09 --- Steepest-Descent [21] 7.06×10-5 1.32 ×10-7 0.031 25 34.7 76 0.81 A. Kumar et al. [18] 1.74×10-5 7.86 ×10-8 0.017 28.31 37 21 0.11 Sahu [17] 8.45×10-5 9.23 ×10-8 0.025 23.03 35.83 109 0.64 Proposed Method 9.65×10-7 1.95 ×10-7 0.0266 33.18 48.91 06 0.028 V. Conclusion A computational efficient method for designing of two-channel QMF bank has been presented in this paper. The prototype filter for the filter bank was designed using polyphase concept to reduce the CPU time. The objective function for the design problem also includes the amplitude distortion term for better results. The improved eigenvalue-eigenvector approach was used for optimization that does not require any matrix inversion which generally affects the effectiveness. The computational burden is very little for the proposed technique in comparison of other state-of-art existing techniques. The proposed method is also very effective for higher filter orders. The extension of this approach for designing more than two-band QMF bank is under investigation. This type of design methods may be suitable various engineering fields such as image and speech compression.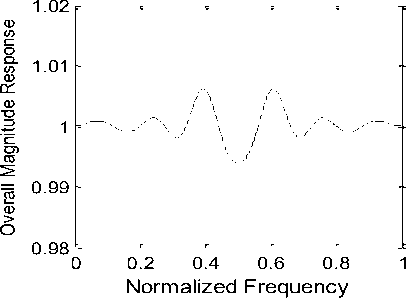
Список литературы Polyphase Structure Based Eigen Design of Two-Channel Quadrature Mirror Filter Bank
- P. P. Vaidyanathan, Multirate systems and filter banks, Prentice Hall, Englewood Cliffs, NJ, 1993.
- Da Chen, Daiming Qu, Tao Jiang, and Yejun He, “Prototype filter optimization to minimize stopband energy with NPR constraint for filter bank multicarrier modulation systems,” IEEE Trans. on Signal Processing, vol. 61, no. 1, pp. 159-169, January 2013.
- S. C. Chan, C. K. S. Pun, and K. L. Ho, “New design and realization techniques for a class of perfect reconstruction two-channel FIR ?lter banks and wavelet bases,” IEEE Trans. Signal Process., 52 (7), pp. 2135–2141, 2004.
- T. Xia, and Q. Jiang, “Optimal multi?lter banks: Design related symmetric extension transform and application to image compression,” IEEE Trans. Signal Process., 47 (7), pp. 1878–1889, 1995.
- M. G. Bellanger, and J. L. Daguet, “TDM-FDM trans-multiplexer: Digital polyphase and FFT,” IEEE Trans. Commun. 22 (9), pp. 1199–1204, 1974.
- M. Vetterli, “Multidimensional sub-band coding: Some theory and algorithms,” Signal Process., vol. 6, pp. 97–112, 1984.
- V. X. Afonso, W. J. Tompkins, T. Q. Nguyen, S. Luo, “ECG beat detecting using filter banks,” IEEE Trans. Biomed. Engg., 46(2), pp. 192-202, 1999.
- S. Chandran, “A novel scheme for a sub-band adaptive beam forming array implementation using quadrature mirror filter banks,” Electron. Lett., 39(12), pp. 891-892, 2003.
- Noureddine Aloui, Ben Nasr Mohamed, Adnane Cherif, "Genetic Algorithm For Designing QMF Banks and Its Application In Speech Compression Using Wavelets", IJIGSP, vol. 5, no. 6, pp. 1-8, 2013. DOI: 10.5815/ijigsp.2013.06.01.
- A. Kumar, G. K. Singh, and R. S. Anand, “An improved method for the designing quadrature mirror filter banks via unconstrained optimization,” J. Math. Model. Algorithm, 9(1), pp. 99-111, 2010.
- Q. G. Liu, B. Champagne, D. K. C. Ho, “Simple design of oversampled uniform DFT ?lter banks with application to sub-band acoustic echo-cancellation,” Signal Process. 80(5), pp. 831–847, 2000.
- C. K. Chen, and J. H. Lee, “Design of quadrature mirror ?lters with linear phase in the frequency domain,” IEEE Trans. Circuits Syst. 39 (9), pp. 593–605, 1992.
- V. K. Jain, and R. E. Crochiere, “Quadrature mirror ?lter design in time domain,” IEEE Trans. Acoust. Speech Signal Process., ASSP-32 (4), pp. 353–361, 1984.
- H. Xu, W. S. Lu, A. Antoniou, “An improved method for the design of FIR quadrature mirror image filter banks,” IEEE Trans. Signal Process., 46 (6), pp.1275–1281, 1998.
- K. Nayebi, T. P. Barnwell III, M. J. T. Smith, “Time domain filter analysis: A new design theory,” IEEE Trans. Signal Process., 40 (6), pp.1412–1428, 1992.
- W. S. Lu, H. Xu, A. Antoniou, “A new method for the design of FIR quadrature mirror-image filter banks,” IEEE Trans. Circuits Syst. II: Analog Digital Signal Process., 45(7), pp. 922–927, 1998.
- O. P. Sahu, M. K. Soni, and I. M. Talwar,” Marquardt optimization method to design two channel quadrature mirror filter banks,” Digital Signal Process., 16(6), pp. 870-879, 2006.
- A. Kumar, G. K. Singh, and R. S. Anand, “An improved method for the design of quadrature mirror filter bank using the Levenberg-Marquardt Optimization;” , DOI: 10.1007/s11760-011-0209-9.
- J. Upendar, C. P. Gupta, and G. K. Singh, “Designing of two channel quadrature mirror filter bank using Partical Swarm Optimization,” Digital Signal Processing, 20(10), pp. 304-313, 2010.
- A. Kumar, G. K. Singh, R. S. Anand, “Design of Quadrature Mirror Filter Bank using Particle Swarm optimization (PSO)”, Int. Journal of Recent Trends in Engineering, vol. 1, no. 3, pp. 213-217, 2009.
- O. P. Sahu, M. K. Soni, and I. M. Talwar, “Designing quadrature mirror filter banks using steepest descent method,” Jorunal of Circuits Systems and Computers, vol. 15, no. 2, pp. 29-42, 2006.
- A. Gupta, and S. K. Agrawal, “Designing of Two Channel Polyphase Quadrature Mirror Filter Bank using Power Optimization Method,” International Conference on Computer & Communication Technology (ICCCT), 2011.
- Pradipta Ghosh, Swagatam Das and Hamim Zafar, “Adaptive-differential-evolution-based Design of two-channel quadrature mirror filter banks for sub-band coding and data transmission,” IEEE Transactions On Systems, Man, and Cybernetics-Part C: Applications and Reviews, vol. 42, no. 6, pp. 1613-1623, 2012.
- Yue-Dar Jou, “Design of two-channel linear-phase quadrature mirror filter banks based on neral networks,” Signal Processing, 87, pp. 1031-1044, 2007.
- S. K. Agrawal, and O. P. Sahu, “Two-Channel Quadrature Mirror Filter Bank: An Overview,” ISRN Signal Processing (Hindawi), vol. 2013, Article ID 815619, 10 pages, doi:10.1155/2013/815619, 2013.
- P. P. Vaidyanathan, “Multirate digital filters, filter banks, polyphase networks and applications: A tutorial,” Proc. IEEE, 78 (1), pp. 56–93, 1990.
- Jyotsna v. Ogale, Alok Jain, "Cosine Modulated Non-Uniform Filter Bank with Improved Computational Efficiency", IJIGSP, vol. 4, no. 2, pp. 1-8, 2012.


