Ползучесть композиционных материалов с абсолютно жёсткими включениями

Рассмотрим многокомпонентный композиционный материал, первый компонент которого является матрицей, а другие – отдельными, хаотически распределенными в матрице

включ ениями различных материалов, имеющ их шар овую форму. Индексом m будем обозначать характеристики материала матрицы, индексом s - материала включений, 5 = 0, 1, 2, ..., n , (индекс 0 соответствует порам).

Запишем локальные уравнения материала

Здесь и далее Г . ( t ) , J m ( t ) - ядро ползучести и функция ползучести (податливость) при 0

чистом сдвиге материала матрицы; _m , – мгновенный модуль упругости сдвига материала матрицы; _m , K_m , _s , K_s – сдвиговые и объёмные модули упругости компонентов композиционного материала; f ij .( r , t ) , £• ( r , t ) – компоненты тензоров напряжений и де-

матрицы ком позиционного материала в виде:

t

² Mm e , (г, t ) = S , (r, t ) + J^r m ⁽ t ^- ^S , (r, )ddT,

£ kk ^(r , t ) = ^67kk ^ t )

3 K m

или:

,

t ei, (r, t) =J Jm (t — )ddSy (r, ^

ekk ^{( r} , t ) =

°kk ^{( r} , t )

формаций; ^^{( г} , t ) = , ^{( r} , t ) ^- 3 jkk ^{( r} , t ) , e y ^{( r} , t ) = e ij ^{( r} , t ) ^- ^5,8_tt ⁽ r , t ) - девиаторные составляющие тензоров напряжений и деформации; _ij – символ Кронекера; t – время; r = ( X 1 , x 2 , x 3 ) .

Функция ползучести материала матри- J ( t )

цы ^m определяется по экспериментальным кривым ползучести при чистом сдвиге (s₁₂ (r, t ) = s ₁₂ (r, 0) = S 0 = const ) :

то есть будем считать, что объёмные деформации не обладают наследственными свойствами. Пусть локальные свойства материалов включений не

проявляют наследственных свойств и имеют вид:

ej^, t ) =

^у ^{( r} , t ) ² Ms

ekk ^{( r} , t ) =

^kk ^{( r} , t )

3 K s

Запи си (1) и (2) девиаторных соотношений для материала матрицы отличаются тем, что в соотношении (2) отсутствует мгновенный модуль упругости сдвига.

J . ( t ) = e ¹²# .             (4)

^S 12

Ядро ползу чести материала матрицы определяется соотнош ением:

г . ( t ) = 2a⁰ dJ m T t ) .           (5)

dt

Применяя к (2), (3) преобразование Лапласа– Карсона, получим в пространстве изображений определяющие соотношения упругого деформирования компонентов композиционного материала:

^Sy ^(r , P ) = ² Ц. ⁽ P ) e ij ^(r , P X

(6) ^kk ^(r) = ³ K m^kk ^(r) ,

S .^(r) = ² M S e i, ^(r) 5 kk ⁽ r) = ³ K_s8_kk ⁽ r) . (7)

,

Здесь чертой сверху обозначены трансфор-

манты Лапласа-Карсона; для постоянных модулей упругости K m = K m , Tl, = И _ , K_s = K_s ;

ZjL m ( p ) = ^——— p — параметр преобразования. ^Jm ⁽ P )

В пространстве изображений соотношения для определения эффективных модулей упруго

сти матричного композиционного материала с шаровыми включениями [1] запишутся в виде:

хотя его компоненты таких свойств не проявляют. Отмеченное свойство объясняется сложным перераспределением во времени системы внутренних напряжений в композиционном материале в процессе его деформирования.

В качестве ядра ползучести материала матрицы рассмотрим ядро вида:

У ⁽ Ps - Рт ⁽ P )) ^Cs«s ⁽ P )

Д * ⁽ P ) = Д т ⁽ P ) + ~------ n----------- c m ⁺У ^Cs«s ⁽ P )

s = 0

_     _ У ( K - K m ) ( P )

K • ( P ) = Km + 2:0------n-----------, cm +У CsYs (P)

s = 0

K

Am (t) = У A.e-"- k=1

Подставляя это выражение в (1), получим

е (л = 212_ e12( t)        0

2Р

kt

1 + У A k J e ^{—l k l, —}° dT

⁰ s 12

2М⁰ 1

k A

1+У т (’—e k=1 Лк

—.

k t

Отсюда и из (4) следует:

1 + 6 Km ^{+ 2} Mm ⁽ P ) ⁽ Ps ^— Pm ⁽ P Д ’

^{5 3 K} m ^{+ 4} Д m ⁽ P ) Д m ⁽ P )

^Y‘ ‘ ^P ) = 1 , X K s - K m ) ’

3 K m + 4Д m ( P )

Jm (t) = e12^ = s12

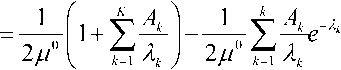
t

Таким образом, в пространстве изображений

эффективный закон деформир ования компози-

ционного материала будет иметь вид:

s i s _y ^{( r} , P )) = ²Д* ⁽ P ) ejiA ’» P )}>

^kk ^{( r} , P Д = ³ K * ⁽ P )(^^{( r} , P )}•

Параметры в выражении функции ползучести можно определить методом наименьших квадратов при сравнении с экспериментальными данными.

В пространстве изображений функция ползучести (14) имеет вид:

Здесь C_m , C_s - объёмные концентрации компонентов композиционного материала, звёздочкой обозначены макроскопические (эффективные) величины, угловыми скобками - средние по объёму ком позиционного материала значения.

Применяя к этим соотношениям операцию обращения и учитывая, что для сдвиговых и объёмных функций ползучести J ( t ) , U ( t ) выполняются соотношения:

J *( P ) = —¹— U *( P ) = -J—_; (11) 2м (P )     ⁴    3 K * ( P ) , ⁽ )

, окончательно найдём макроскопический закон ползучести:

t

/ X x \           Г XT * X           X , X / X X \ X

\ey(t)/ ==J J (t- )dd(\s4 M/)’ t                                       (12)

(^kk ⁽ t )) = J U * ⁽ t ^- )d ^{d (}(^ kk ⁽ H) )•

^Jm ⁽ P ) =

Из (15) получим:

P m ⁽ P ) =

2" J m ( P )

Из выражений (8), (9), (10), (11), (12) следует, что композиционный материал обладает объёмными наследственными свойствами,

¹ A k ^P

2м0 ty \ p + Xk"

В предположении, что C ₀ = 0 (композиционный материал не содержит пор) и включения матр ично го композиционного материала являются абсолютно жёсткими, то есть, m_s ^^ю , s = 1, 2, ..., n из (8), (9) следует:

5 c       ММ

*1 ⁽ P ) = Рт ⁽ P ) I ^{1 +} т;—I ^c = У ^Cs , ⁽¹⁷⁾ V 21 — C ;      1:1

, или с учётом (16):

то есть:

A * ( p ) =

1 I 1 5 c )

• 1 +             ,

2 J m ( P ) I ²¹ - C )

J (p)=

2M*( P)

^Jm ⁽ P )

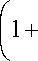
5 .)

21 - c J

После применения обратного преобразования Лапласа - Карсона, получим эффективную функцию ползучести рассматриваемого композиционного материала:

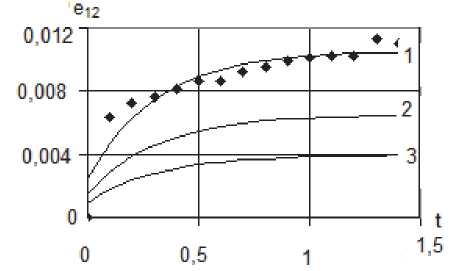
Рис. 1. Кривые ползучести материала матрицы ( c = 0) и композиционного материала при различных объёмных концентрациях абсолютно жёстких включений;

– экспериментальные данные;

1 - ( c = 0) ; 2 - ( c = 0,1) ;3 — ( c = 0,4)

J * ( t ) =

2M0

x

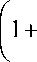
⁵ JL_ T ¹

21 - c J

Рассмотрим соотношение

) e- ^

J

x

t

(e 1 ₂ ⁽ t )) = J J * ⁽ t — )d а^ 12 ⁽ t )),     (21)

после интегрирования которого запишем макроскопический закон ползучести композиционного материала в виде:

( ^e 12 ⁽ t ))

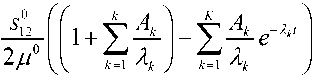
x

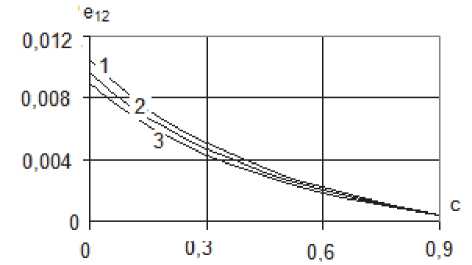
Рис. 2. Зависимости значений деформации

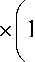
5 c ^ ¹ 21 - c ^J

композиционного материала от объёмной концентрации абсолютно жёстких включений в различные моменты времени;

1 - ( t = 1,5) ; 2 - ⁽ t = ^0,7) ; 3 - ⁽ t = ^0,5)

Для модельного композиционного материала с абсолютно жёсткими включениями на рис. 1 приведены экспериментальные и расчётные значения кривых сдвиговой ползучести при различных объёмных концентрациях включений; на рис. 2 – зависимости значений деформации композиционного материала от объёмной концентрации включений в различные моменты времени. Время t измеряется в условных единицах.