Помехоустойчивость алгоритмов приёма сигналов с многоимпульсной позиционно-импульсной модуляцией

Лазерная техника открывает большие возможности для совершенствования систем связи, локации и радиоуправления. Эти возможности связаны, в первую очередь, с громадным коэффициентом усиления передающих оптических антенн, что позволяет получить большое отношение сигнал/шум в приемнике в широкой полосе частот при маломощном передатчике, а также с возможностью использования очень широкой полосы частот при передаче и приёме оптических сигналов. Мощность передатчика во многом определяется используемым методом модуляции. Одним из наиболее выгодных методов передачи сообщений в лазерных системах связи с прямым детектированием, позволяющих использовать передачу с минимальной мощностью, является цифровая позиционно-импульсная модуляция (ПИМ или PPM в английской аббревиатуре ( PulsePosition Modulation )) [1]. Как показано в [2], для классических оптических каналов при ограничениях на пиковую и среднюю мощности, PPM может обеспечить близкую к оптимальной ёмкость канала. Подобный метод модуляции широко используется в оптоволоконных и спутниковых системах [3, 4], кроме того, он применяется и в сверхширокополосных радиокоммуникационных системах [5].

При классическом способе формирования сигналов с PPM символьный интервал [0; T ] разбивается на

L подынтервалов (слотов) длительностью τ ₀ каждый. Передаче l -го символа соответствует передача импульса с временным положением ( l – 1) τ ₀. Очевидно, максимальное количество возможных передаваемых сообщений в этом случае не превосходит L . Интересной альтернативой PPM является многоимпульсная позиционно-импульсная модуляция ( Multipulse PulsePosition Modulation (MPPM)) [6], которая имеет преимущества по сравнению с классической PPM в уменьшенном отношении пиковой мощности к средней. При таком подходе передаётся уже не один, а K импульсов в течение тех же L слотов. В этом случае количество передаваемых сообщений существенно увеличивается по сравнению с классической PPM. Например, если количество слотов L = 10, то при классической PPM можно осуществить передачу 10 различных сообщений (отличающихся временными положениями передаваемых импульсов), в то время как при использовании MPPM количество разных сообщений будет определяться числом сочетаний С_L^K (например, при L = 10 и K = 2 это количество становится равным 45). Следует отметить, что MPPM превосходит PPM также по частотной эффективности [7].

В дальнейшем будут рассматриваться многоимпульсные PPM (MPPM) с точки зрения разработки новых методов их демодуляции. Существующие методы приёма (демодуляции) таких сигналов основы- ваются на методах турбодекодирования с использованием алгоритма Витерби с мягким принятием решения [8], что бывает не просто реализовать на практике. Учтём, что информация о передаваемых сообщениях закодирована во временных положениях (позициях) передаваемых K импульсов. Следовательно, демодуляция (приём) может заключаться в оценке этих временных положений. Однако при цифровой обработке таких сигналов могут возникнуть сложности, связанные с необходимостью обработки огромного количества отсчётов и их перебора. Отметим, что аналогичные проблемы возникают везде, где используется поток коротких импульсов, например, при исследовании нейронной активности, при формировании и обработке биоизображений [9], при сверхширокополосной связи [10] и пр.

1. Алгоритм оценки временных положений и амплитуд периодической последовательности сверхкоротких импульсов с использованием идеального фильтра нижних частот

Постановка задачи

Предположим, что излучаемый сигнал представляет собой сумму K достаточно коротких импульсов, в идеале – дельта-функций. Представим такой сигнал в виде K - 1      ∞

s ( t) = Е A k Е ^§ ( t - t k - nT ),                   (1)

k=0 n=-∞ где Ak и tk – амплитудные множители (в дальнейшем просто амплитуды) и временные положения отдельных импульсов на периоде T, предполагаемые априори неизвестными, а число таких импульсов K на периоде предполагаем известным. Теоретически спектр такого сигнала бесконечен, что при дискретизации потребует бесконечно малого интервала дискретизации (бесконечно большого количества отсчётов). Пройдя среду распространения с известной импульсной характеристикой, дельта-импульсы расширяются во времени так, что вместо (1) полезный сигнал будет иметь вид

K - 1      ∞

s ( t) = Е A k Е F ( t - t k - nT ),                   (2)

k=0 n=-∞ где F(t) – известная функция времени, описывающая форму импульсов, прошедших канал распространения и получающихся в результате вычисления свёртки входного сигнала с импульсной характеристикой канала. Подобный сигнал будет иметь вид также на выходе преобразователя лазерного (инфракрасного) излучения в электрические импульсы. Для такого преобразования обычно используется детектор сигнала (pin-фотодиод) [11].

Учитывая периодический характер, представим сумму по n в (2) в виде ряда Фурье

∞∞

Е F ( t - nT) = Е fm exp(2 n jmt I T), n =-∞              m =-∞

1T где f =    F(t) exp(-2πjmt/T) dt .

m _{T 0}

Тогда (2) перепишется как

K -1

s ⁽ t ) = Е A k Е f m exP^{(2 n jm (} t ^- t k )/^T ) = k = 0 m =-∞

∞

= Е fm exp(2njmtIT)Е Ak exp(-2njmtk IT) = m=-∞

∞

= Е fmXm exP(2njmt/T), m=-∞ где

K - 1

Xn=Е Ak exp(-2njntk / T) ■ k=0

Учтём, что в оптической связи длительности импульсов, описываемых функцией F ( t ), чрезвычайно малы (пикосекунды и менее). Следовательно, при их цифровой обработке потребуется огромное количество отсчётов, что в настоящее время может привести к существенным аппаратным и финансовым затруднениям. Поэтому для уменьшения ширины спектра подадим такой сигнал на идеальный фильтр нижних частот (ФНЧ) с импульсной характеристикой вида h ( t ) = B sinc ( π Bt ), где sinc ( x ) = sin ( x ) / x . Частота среза такого фильтра равна π B рад/с, в дальнейшем, не умаляя общности, будем считать величину π B чётной. В результате на выходе такого фильтра сигнал примет вид

s(t ) = j s ( v ) h ( t -v )d v = -∞

∞∞

= Е f m X m j exp(2 n jm v I T)h ( t -v )d v =

-∞

m =-∞

( 2nm ^

= Е fmXmH 1^-1 exP(2njmt/T)■ m=-^          x 1 7

Здесь H ( ω ) – частотный коэффициент передачи рассматриваемого идеального ФНЧ с импульсной характеристикой h ( t ).

С учётом того, что H (2 π m / T )=0 при | m |> BT /2= M , имеем

M

»(t) = Е fmXm eXP(2njmt/T) = m=-M

M

= Е X1 m exp(2njmtIT), m=-M

где X 1 m = f m X m .

Несложно заметить, что максимальная частота в спектре сигнала (4) равна π B , что и следовало ожидать, т.к. широкополосный сигнал (2) был пропущен через идеальный ФНЧ с частотой среза π B . Следовательно, его можно продискретизировать в соответствии с теоремой отсчётов с шагом ∆ t ≤ π / π B = 1/ B . Причём количество необходимых отсчётов на периоде N становится весьма небольшим: N ≥ T / ∆ t + 1 = 2 M + 1 . Учтем также, что X_n – отсчёты суммы K комплексных экспонент (3). Как известно [12], для нахождения их амплитуд и фаз достаточно иметь N ≥ 2 K отсчётов. Однако M = BT / 2. Следовательно,

_{B ≥} 2 K _.

T

Таким образом, оказывается, что параметр B идеального ФНЧ определяется количеством импульсов на периоде K , а число необходимых отсчётов выходного сигнала фильтра

M                        ________ sn = E X1 m exp(2njmnAt / T), n = 0, N-1,     (6)

m=-M должно удовлетворять условию

N >  2 K + 1,                                  (7)

и, следовательно, зависит лишь от количества импульсов на периоде, а не от их длительности.

Итак, если сигнал (2) предварительно подать на ФНЧ с указанными характеристиками, то дискретная обработка выходного сигнала фильтра потребует незначительного количества равноотстоящих отсчётов, зависящих не от спектральных характеристик входного сигнала, а от количества этих сигналов. Таким образом, с учётом вышеизложенного, задача определения временных положений t_k и амплитуд A_k импульсов в (2) сводится к следующему. Выбираем идеальный ФНЧ с параметром (5) и подаём на него сигнал (2). Выходной сигнал этого фильтра равномерно дискретизируем на периоде T , получая N отсчётов (6), количество которых удовлетворяет условию (7). Формула (6) представляет собой, по сути, систему из N уравнений с 2 М + 1 неизвестными X n . Если отношение T / A t выбрать целым, то эта система уравнений легко решается. Например, если T / A t = N , то (6) - это обычное обратное дискретное преобразование Фурье. Следовательно, X_n может быть найдено как прямое преобразование Фурье от s i n . Если T / A t <  N , то её решение может быть найдено через псевдообращение матрицы. Таким образом, находим N отсчётов X_n , которые в соответствии с (3) представляют собой сумму K комплексных экспонент с амплитудами A k и временными положениями t k . Как известно [12], при выпол нении условия (7) эти параметры ( A k и t k , n = 0, K - 1) могут быть найдены любыми известными способами. В частности, для решения подобной задачи могут быть использованы методы Прони [13], Annihilating Filter [14], MUSIC [13] и пр.

Отметим, что рассмотренная выше задача является идеализированной, прежде всего, из-за отсутствия в наблюдаемых данных всегда присутствующих в реальности случайных искажений – шумов. Представим наблюдаемые данные в виде аддитивной смеси сигнала (2) и гауссовского белого шума n ( t ) с односторонней спектральной плотностью мощности N ₀: x ( t ) = s ( t ) + n ( t ). Тогда на выходе идеального ФНЧ будем иметь y ( t ) = .?( t ) + n(t ), где i ( t ) описывается формулой (4), а n ɶ ( t ) – гауссовский центрированный случайный процесс с корреляционной функцией K ( t ) = ( N ₀/2) B sinc( n B т ). Тем не менее, и в этом случае для нахождения оценок параметров A k и t k , n = 0, K - 1, сигнала (2) можно воспользоваться аналогичным подходом, описанным выше, и применить перечисленные методы анализа [13, 14], а также метод Cadzow [15], специально разработанный для работы в шумах.

Результаты моделирования

В среде Matlab было выполнено моделирование алгоритмов оценки временных положений t ^ˆ _k и амплитудных множителей A ^ˆ _k сигнала (2), наблюдаемого на фоне аддитивного гауссовского шума. С этой целью формировались отсчёты процесса y ( t ) с шагом, обеспечивающим среднеквадратическую погрешность аппроксимации, не превышающую 10 %. По каждой сформированной реализации с использованием алгоритмов Annihilating Filter, Cadzow и MUSIC находились оценки t k и A k ( k = 1, K ) при разных значениях K и отношениях сигнал/шум (ОСШ) z ² , выраженного в децибелах (дБ). Далее определялись нормированные рассеяния оценок временных положений и амплитуд импульсов

K - 1            2

V=   2 E (?k - tk) и

KT k = 0

• 1        K - 1 -         \²

VA = -K-1   E ( "Ak - Ak )

K E A k ^{2 k} = 0 k = 0

для всех алгоритмов и для всех (не менее 10000) испытаний. Окончательные значения рассеяний V t и V A получались путём усреднения по всем испытаниям (опытам). При моделировании использовались специальные функции, реализующие алгоритмы Annihilating Filter, Cadzow и MUSIC. Первые две из них были написаны самостоятельно, а для реализации третьего алгоритма использована функция rootmusic из библиотеки Matlab. На рис. 1 и 2 изображены зависимости этих нормированных рассеяний от ОСШ z ² (дБ). Кривые 1 построены с использованием метода Annihilating Filter, кривые 2 – с использованием метода Cadzow и кривые 3 – с использованием метода MUSIC. Сплошными линиями изображены соответствующие зависимости при K = 2, а штриховыми – при K = 7 (для рис. 1) и K = 5 (для рис. 2).

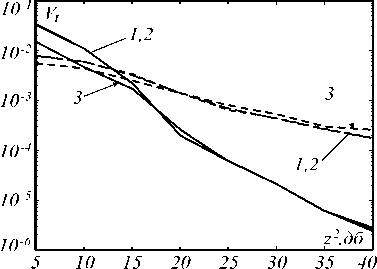
Рис. 1. Зависимость нормированного рассеяния оценки временных положений от отношения сигнал/шум

Анализ приведённых рисунков свидетельствует об ухудшении точности оценок рассматриваемых параметров с увеличением количества сигналов K . Кроме того, приведённые результаты свидетельствуют о том, что используемые методы оценки (Annihilating Filter, Cadzow, MUSIC) обладают приблизительно одинаковой точностью.

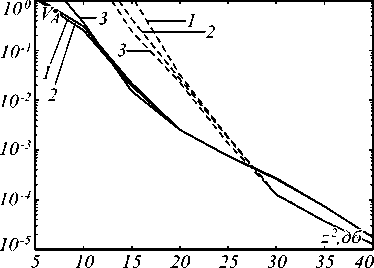
Рис. 2. Зависимость нормированного рассеяния оценки амплитуд от отношения сигнал/шум

Действительно, на рис. 1 и рис. 2 кривые 1–3 отличаются друг от друга в пределах погрешности измерений. Поэтому в дальнейших исследованиях использовался только один из этих методов – алгоритм MUSIC. Следует, однако, отметить, что при моделировании временные положения импульсов выбирались хотя и случайным образом, но при некотором ограничении.

Это ограничение выглядит следующим образом: минимальное расстояние между двумя соседними импульсами должно быть не меньше, чем T /10. Если уменьшить это минимальное расстояние между соседними импульсами, то точность измерения резко падает.

Приведённые результаты были получены в соответствии с (7) при наименьшем возможном количестве отсчётов N = 2 K + 1. В работе было выполнено также моделирование аналогичных алгоритмов с увеличенным количеством отсчётов N . При этом было показано, что увеличение этого количества отсчётов приводит к повышению точности оценок соответствующих параметров. Например, при K = 5 увеличение количества отсчётов с минимально необходимых N = 2 K + 1 = 11 до 17 позволило уменьшить рассеяние оценок временных положений приблизительно в полтора раза при не очень малых значениях ОСШ.

Такой фильтр широко используется в качестве сглаживающего фильтра, предназначенного для компенсации искажений, вносимых каналом связи. Изменение параметра в этого фильтра приводит к изменению формы его АЧХ. Так, при в = 0 из (8) получаем рассмотренный ранее идеальный ФНЧ, а при в = 1 — это будет известный фильтр типа приподнятого косинуса.

Результаты моделирования

Выполним моделирование рассмотренных алгоритмов оценки временных положений и амплитуд импульсов, заменив в них идеальный ФНЧ на фильтр Найквиста (8). При расчётах, очевидно, необходимо будет изменить характеристики шума на выходе этого фильтра, так как они будут отличаться от аналогичных характеристик на выходе идеального ФНЧ. Результаты моделирования при использовании фильтра Найквиста приведены на рис. 3–5.

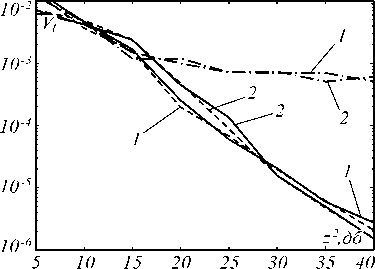
Рис. 3. Зависимость нормированного рассеяния оценки временных положений от отношения сигнал/шум

2. Алгоритм оценки временных положений и амплитуд периодической последовательности сверхкоротких импульсов с использованием фильтра Найквиста

Постановка задачи

Одним из возможных недостатков изложенного подхода к оценке временных положений и амплитуд импульсов в (2) является использование идеального ФНЧ, который, как известно, не реализуем на практике. В связи с этим рассмотрим возможность замены этого фильтра на другие. В частности, используем для подобной замены фильтр, относящийся к классу фильтров Найквиста с амплитудно-частотной характеристикой (АЧХ) вида [16]

1, |ю|<л B (1 -в ),

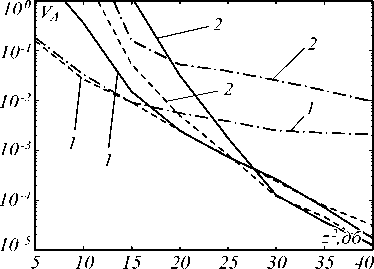
Рис. 4. Зависимость нормированного рассеяния оценки амплитуд от отношения сигнал/шум

| H (®)| = J 2

1 + cos

H-n B l- P )

(    2в B    J

л B (1 -в ) <|ю|<л B (1 + ₽ ), 0, |и|>л B (1 + в ).

0.2     0,4      0,6      0,8     1,0

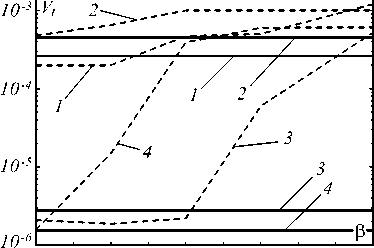
Рис. 5. Зависимость нормированного рассеяния оценки временных положений от параметра фильтра Найквиста β

Для исследования степени влияния параметров этого фильтра на характеристики оценок временных положений и амплитуд импульсов на этих же рисунках приведены соответствующие характеристики оценок и для идеального ФНЧ.

Так, на рис. 3 сплошными линиями изображены нормированные рассеяния оценок временных положений при использовании идеального ФНЧ, штриховыми линиями – нормированные рассеяния оценок временных положений при использовании фильтра Найквиста при в =0,1, а штрихпунктирными линиями - аналогичные зависимости при р = 1. Кроме того, кривые 1 на этом рисунке построены при K =2, а кривые 2 – при K =5.

На рис. 4 приведены аналогичные зависимости, только для рассеяний оценок амплитуд импульсов.

Анализ приведённых зависимостей свидетельствует о следующем. Применение фильтра Найквиста, вместо идеального ФНЧ, вполне допустимо при выборе не очень больших значений параметра р . Так, независимо от количества импульсов и при любых (не очень малых) ОСШ, рассеяния оценок временных положений при использовании фильтра Найквиста незначительно отличаются от аналогичных характеристик при использовании идеального ФНЧ при р = 0,1. Увеличение параметра р приводит к ухудшению точности оценок временных положений импульсов, начиная примерно с z ² > 20 дБ. Что касается оценок амплитуд импульсов, то в этом случае выбор параметра фильтра Найквиста р оказывает несколько более существенное влияние на характеристики этих оценок. Замена идеального ФНЧ на фильтр Найквиста при р = 0,1 целесообразна при не очень малых значениях ОСШ (если K = 2 – при z ² > 20 дБ, в то же время, если K = 5, то уже при z ² > 30 дБ).

Рассмотрим более подробно влияние параметра фильтра Найквиста р на характеристики оценок временных положений импульсов (как наиболее информативных параметров по сравнению с амплитудами). Это влияние можно проследить из анализа рис. 5, на котором изображены нормированные рассеяния оценок временных положений импульсов при использовании как идеального ФНЧ (сплошные линии), так и фильтра Найквиста (штриховые линии). На этом рисунке кривые 1 построены при K = 2 и z ² > 20 дБ, кривые 2 – при K = 5 и z ² > 20 дБ, кривые 3 – при K = 2 и z ² >40 дБ, кривые 4 – при K = 5 и z ² >40 дБ.

Анализ приведённых зависимостей показывает, что замена идеального ФНЧ на фильтр Найквиста действительно целесообразна лишь при выборе малых значений параметра р . Например, при K =2 параметр р< 0,3 ^0,5, а при K = 5 параметр р не должен превышать 0,1.

• 3. Оценка временных положений и амплитуд импульсов последовательности классическим методом максимального правдоподобия

Рассмотрим теперь возможность решения поставленной задачи (оценка временных положений и амплитуд импульсов последовательности (2)) классиче- ским методом максимального правдоподобия. Для этого в соответствии с (3) предположим, что наблюдению доступны N отсчётов аддитивной смеси полезного сигнала (6) и гауссовского центрированного случайного процесса с элементами корреляционной матрицы вида Kj = (N0/2)Bsinc(nBAt(i-j)), i, j = 1, N : Yi = si + ni. Необходимо определить оценки параметров tk и Ak (k = 1, K). В соответствии с методом максимального правдоподобия ищется логарифм функции правдоподобия, который в нашем случае выглядит следующим образом:

N - 1 N - 1

Л [ t , A ] = EE ( Y - m i ( t , A ) ) ( Y j - m j ( t , A ) ) C j , (9) i = 0 j = 0

где m i ( t , A ) = s , C j - элементы матрицы, обратной корреляционной матрице шума с элементами K ij .

Оценки амплитуд импульсов можно достаточно просто найти из решения системы уравнений ( дЛ / д A )|- = 0, l = 1, K . Действительно, вектор оценок амплитуд можно представить в виде A = uR ^-1, где u – вектор размера 1× K с элементами

N - 1 N - 1

U = EE C j YG i ( j A t ), i = 0 j = 0

' a0 Рс,1 в0,2". ₽0,k-1 ) R= Р,0 ... a1 ... в1,2... ... P1,K-1 ... ч в K-1,0 в K-1,1 в K-1,2... a K-1 y матрица размера K×K с элементами

N - 1 N - 1

a i = EE C ij G i ( i A t ) G ( j A t ), i = 0 j = 0

N - 1 N - 1

в i , k = EE j ( i A t ) G k ( j A t ). i = 0 j = 0

Значительно сложнее дело обстоит с оценкой временных положений импульсов tk сигнала (2). Для этого найденные оценки амплитуд Aˆk необходимо подставить в (9), в результате получится функция Л, зависящая от K переменных tk. Необходимо осуществить поиск абсолютного максимума этой многомерной функции. Подобная задача может быть решена без существенных вычислительных затрат лишь для K = 1 и K = 2. Увеличение количества импульсов в наблюдаемых данных на единицу приводит к тому, что всякий раз размерность функции Л будет увеличиваться в Nt2 раз, где Nt – количество отсчётов по возможным временным положениям функции правдоподобия. В связи с вышеизложенным в работе была выполнена оценка по методу максимального правдоподобия параметров tk и Ak (к = 0, K -1) только для случая K=2. Как показали расчёты, точность этих оценок не существенно отличается от точности оценок анализируемых параметров, производимых предлагаемым в работе методом, что подтверждает его высокую эффективность. Действительно, при K = 2 и z2 ≤ 40 дБ рассеяние оценки временных положений при использовании метода максимального правдоподобия отличается от рассеяния оценки по предложенному методу не более, чем на 30 %. Отличие рассеяний оценок амплитуд для этих методов для тех же условий не превышает 50 %. Однако ещё раз подчеркнем, что практическая реализация алгоритма оценки временных положений и амплитуд импульсов по методу максимального правдоподобия уже при K ≥ 3 весьма затруднительна (временные затраты возрастают настолько, что оценки не могут быть найдены в реальном режиме времени). Следовательно, несмотря на некоторый проигрыш в эффективности измерений, в реальных условиях целесообразно использовать предлагаемый в работе алгоритм вместо алгоритма максимального правдоподобия.

Отметим, что приведённые результаты справедливы в случае, если количество импульсов на периоде K априори известно. В то же время значительный интерес может представлять аналогичная задача при неизвестном количестве импульсов. Решение этой задачи может быть выполнено, например, с использованием теории Compressive Sensing [17–19], однако решение подобной задачи оставим на будущее.

Заключение

В работе показано, каким образом можно оценивать временные положения и амплитуды периодической последовательности импульсов по незначительному, зависящему лишь от числа этих импульсов количеству отсчётов. Определены условия, при которых вместо идеального ФНЧ можно использовать фильтр Найквиста. Показано, от чего зависит выбор параметров этого фильтра. Отмечено, что в отличие от метода максимального правдоподобия практическая реализация предложенного алгоритма значительно более простая, не требующая формирования и поиска максимума функции большого числа переменных. В то же время характеристики точности оценок временных положений и амплитуд импульсов при использовании этих двух методов отличаются незначительно. Показано, что, если точность оценки временных положений при использовании минимально необходимого числа отсчётов N = 2K + 1 недостаточна, можно несколько повысить эту точность путём незначительного увеличения количества этих отсчётов. Действительно, как показано ранее, увеличение количества отсчётов приблизительно в 1,5 раза (от 11 до 15–17) от минимально необходимого приводит к повышению точности измерения временных положений не менее чем в 1,5 раза (при не очень малых значениях ОСШ z2 ≥ 20 дБ). Однако дальнейшее увеличение количества используемых отсчётов не приведет к существенному выигрышу в эффективности оценки временных положений. В то же время подобное увеличение количества отсчётов, как показывают исследования, практически не оказывает никакого влияния на эффективность оценки амплитуд. Таким образом, в оптических системах с MPPM, в которых количество K передаваемых импульсов определяет не только энергетическую и частотную эффективности, но и скорость передачи информации, использование предлагаемого подхода позволяет осуществлять детектирование без существенных временных и аппаратных затрат с достаточно высокой точностью.