Помехоустойчивость и помехозащищенность командной радиолинии управления, работающей с широкополосными ЛЧМ-сигналами

Ш ирокополосные сигналы с линейной частотной модуляцией впервые нашли применение в радиолокации для ликвидации извечного противоречия между дальностью обнаружения и разрешающей способностью [1]. Представляет интерес оценка того, в какой степени и для каких помеховых условий оправдано применение таких сигналов в командных радиолиниях, в которых помехоустойчивость системы оценивается с использованием статистического критерия оптимального обнаружения сигнала – критерия Неймана–Пирсона, который характеризует прием команд не только при наличии полезного сигнала (правильный прием), но и при его отсутствии (ложный прием).

В работе рассматривается радиолиния управления, работающая с сигналами относительной фазовой телеграфии (ОФТ), в которых широкополосность сигнала достигается путем линейной частотной модуляции (ЛЧМ) каждого символа двоичной комбинации. За время, равное длительности символа Т_э , частота передаваемого сигнала будет изменяться по линейному закону от f₁ до f₂ , при этом спектр излучаемого широкополосного ЛЧМ-сигнала будет иметь форму, близкую к прямоугольной, а ширина спектра будет практически равна

∆f = f 2 – f 1

Модель радиолинии показана на рис. 1.

Рис. 1. Модель радиолинии, работающей с широкополосными ЛЧМ-сигналами

Модель содержит полосовой фильтр Ф , перемножитель сигналов X , линию задержки ЛЗ , фильтр нижних частот ФНЧ , согласованный фильтр СФ , ограничитель О , декодирующее устройство ДУ и пороговоеустройство ПУ . Полосовойфильтр Ф настроен на среднюю частоту широкополосного сигнала f₀ = 0,5(f₁ + f₂) и имеет АЧХ почти прямоугольной формы с полосой пропускания, совпадающей с шириной спектра широкополосного сигнала. В линии задержки ЛЗ сигнал задерживается на время, равное длительности двоичного символа Т_э . На выходе фильтра нижних частот ФНЧ выделяется двоичный видеосигнал, с элементом которого согласован фильтр СФ .

Командные радиолинии управления с точки зрения информационного назначения относятся к классу радиотехнических систем передачи информации – дискретных сообщений (команд). В них, в отличие от систем связи, помехоустойчивость системы оценивается критерием, который характеризует прием команд не только при наличии полезного сигнала (правильный прием), но и при его отсутствии (ложный прием) – статистическим критерием Неймана–Пирсона. При этом помехоустойчивость командной радиолинии оценивается двумя основными параметрами – вероятностями Р_л1 и Р_к . На практике удобно дополнительно использовать (особенно при сравнении различных вариантов построения) и такие параметры, как коэффициенты помехоустойчивости и помехозащищенности. За коэффициент помехоустойчивости К_пу принимается отношение напряженности Е_п поля флюктуационных (шумовых) помех, взятой в полосе 1 кГц, к напряженности Е_с поля сигнала в точке приема, при котором Р_к = 0,5 [2]. Можно также оперировать не с напряженностями поля, а с напряжениями на входе приемного устройства. За коэффициент помехозащищенности К_пз принимаются аналогичные отношения, но в полосе по всей ширине спектра широкополосной преднамеренной помехи или только в полосе помехи, равной информационной полосе сигнала.

рокополосной радиолинии будет производиться при следующих исходных данных:

• ♦    заданная вероятность ложного приема команды от случайных помех за время Т_а = 8,64 ×10⁵ с составляет Р л1 = 10^-5 ;

• ♦    заданная вероятность воспроизведения команды противоборствующей стороной за то же время при условии, что рабочая частота радиолинии известна, равна Р л2 = Р л1 = 10^-5 ;

• ♦    ширина спектра широкополосного сигнала Af = 2 МГц;

• ♦    длительность команды управления Т к = l c;

• ♦    разрядность кода n = 64 .

Примечание. При обработке ОФТ-сигнала теряется один разряд двоичной комбинации, поэтому далее при расчетах будет использоваться n = 63 .

Известно, что вероятность ложного приема одноблочной команды от случайных помех определяется по формуле где Cni – число сочетаний из n по i

C _n i

n

s!(n - s)!

В нашем примере неравенство (1) выполняется при s = 5 .

Как отмечалось выше, помехоустойчивость радиолинии будет оцениваться по величине коэффициента К_пу , за который принимается отношение напряженности поля помех Е_п , взятой в полосе 1 кГц, к напряженности поля сигнала Е_с в точке приема, при котором вероятность правильного приема команды Р_к равно 0,5. За коэффициент К_пз принимается отношение Е_п /Е_с в полосе, равной полосе широкополосной помехи.

При достаточно большой разрядности кода вероятность правильного приема символа двоичной комбинации, соответствующую Р_к = 0,5 , можно определить по простой формуле

Рэ = 1 – s/n

Постановка и решение задачи

Предполагается, что команда управления состоит из одного блока двоичной комбинации с разрядностью n . Команда считается принятой правильно при правильном приеме n - s символов из n , т.е. допускается не более s ошибок в приеме символов, причем место ошибки может быть любое.

Оценка помехоустойчивости и помехозащищенности ши-

В нашем примере имеем Р_э = 58/63 = 0,9206.

Процесс на выходе согласованного фильтра имеет нормаль-

ное распределение, следовательно, вероятность правильно-

го приема символа будет равна

Р э = Ф

V

U m σ 1

д

= Ф (q 1),

где Ф(х) – интеграл вероятности Лапласа.

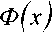
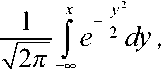
где U_m – амплитуда видеосигнала;

σ₁ - СКО шума в полосе согласованного фильтра СФ, определяемое исходя из мощности шума σ₁² в этой полосе;

q₁ – отношение с/ш на выходе фильтра СФ, которое в нашем примере равно q₁ = U_m /σ₁ = F(P_Э) = 1,409 , где F(x) – функция, обратная интегралу вероятности Лапласа.

Коэффициенты помехоустойчивости и помехозащищенности широкополосной радиолинии найдем, пересчитав отношение с/ш q₁ к полосе частот 1,0 кГц и к полосе пропускания фильтра Ф соответственно. На выходе перемножителя получаем произведение z(t) двух суммарных процессов

z(t) = [s(t)+x(t)] [s(t–T)+x(t–Т)] = s(t) s(t–T) + s(t) x(t–T) +

+ x(t) s(t–T) + x(t) x(t–T),                                 (4)

где s(t) – широкополосный ЛЧМ-сигнал на выходе фильтра Ф ; x(t) – узкополосный шумовой процесс в полосе фильтра Ф ; Т – время задержки, равное длительности Т_э .

При перемножении сигнал и помеха вступают друг с другом во взаимодействие, и процесс на выходе перемножителя содержит три составляющие:

• ♦    СС — составляющую, обусловленную взаимодействием сигнала с самим собой (взаимодействие задержанного сигнала с незадержанным);

• ♦    ХХ — составляющую, обусловленную взаимодействием помехи с самой собой (взаимодействием задержанного шума с незадержанным);

• ♦ СХ — составляющую, обусловленную взаимодействием сигнала с помехой.

Составляющая СС образует сигнал, а составляющие XX и СX – помеху на выходе перемножителя.

Перейдя к автокорреляционным функциям этих составляющих и определив спектральную плотность мощности шума на выходе фильтра ФНЧ , найдем отношение с/ш в полосе согласованного фильтра СФ .

Автокорреляционная функция (АКФ) процесса на выходе перемножителя определяется выражением где Rс(θ) – АКФ широкополосного сигнала; Rс2(θ)– АКФ квадрата этого сигнала; Rх(θ) – АКФ узкополосного шума, действующего на выходе перемножителя.

АКФ узкополосного шума определяется по формуле

R_x ( 6 ) ^- о 2

sin (^9/2) ( ^ о 6 X 2)

cos ( о 6 ) ,

где σ² – мощность узкополосного шума на выходе фильтра Ф ; ω₀ – частота настройки фильтра Ф ; ∆ω – полоса пропускания фильтра Ф .

В рассматриваемом случае автокорреляционную функцию сигнала определим, пренебрегая ЛЧМ

V ²

R_c( 6 ) = -у cos ( ^ о 6 ) .                   (7)

Мощность СС-составляющей процесса на выходе фильтра ФНЧ (мощность сигнала) равна

P _{С С} = R ( 0 ) = V ^m .                           (8)

Низкочастотная часть АКФ СХ-составляющей шума, действующая на выходе фильтра ФНЧ, равна

2 ₂s/n(^M)_

^R cx⁽ 9 ) V    (Д _ю6/2)    ,            ⁽⁹⁾

а низкочастотная часть АКФ ХХ-составляющей шума равна

R XX ( 0 ) = у X

sin ² ( 2 to 0 /2 ) ( ^ to0 /2У

Определим по формуле Винера–Хинчина спектральные плотности мощностей СХ- и ХХ-составляющих шума

W_a( m ) = 4 J R_a< e ) cos ( me )d m =

8V ² о ² 7 sin ( A me /2)

= —m — J — ^-------- cos ( me )d e    ⁽¹¹⁾

A m о e         '

∞ w„ (m) = 4 f R„(6 ) cos(rn9 )d0 =

2 q ⁴ 7 sin ²( A toO /2)

= ( i my !—9 ^^{cos ( ю6 )d 6} =

= -5^( 1 - m / Д га ) .                   (12)

2 ^ f

При ω = 0 имеем

Wxx (0) = — .                      (13)

XX^{х 7}    2 A f

Имея в виду, что полоса пропускания фильтра Ф во много раз превышает полосу пропускания согласованного фильтра, определим мощности составляющих шума СХ и ХХ в полосе согласованного фильтра:

x-2x = W-x (x-x)№ = -V- ,(14)

CXCX

2m1

< = Wxx -0)AF = 2m- •<

Здесь m₁ = Δf/ΔF – отношение полос пропускания фильтров Ф и СФ .

Отношение с/ш в полосе согласованного фильтра СФ равно q 2 =   P CC    =    V m4 m 1    = 2 q 4 m 1 .(16)

¹   σ C ² X +σ X ² X    2 ( V m ²σ²+σ⁴ ) 2q²+1

Поскольку в полосе фильтра Ф величина q₂ во много раз меньше 1, можно пользоваться упрощенной формулой

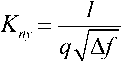
q 12 = 2 m 1 q 4 ,                                   (17)

откуда следует

q 2 =

q 1

где ∆f – полоса пропускания согласованного фильтра Ф в кГц.

Поскольку полоса пропускания согласованного полосового фильтра равна

∆f = 1/Тэ = 0,063 кГц ,

В нашем примере q₁ = 1,409 , m₁ = 31746 , следовательно, получаем q = 0,0748 .

Таким образом, коэффициент помехозащищенности радиолинии управления, работающей широкополосными ОФТ+ЛЧМ сигналами с параметрами, приведенными в исходных данных, составляет

К пз = 1/q = 13,37,

а коэффициент помехоустойчивости при этом будет равен [2]

к п у

Кпз = 13,37 = f ^2000

0,299

.

Полученное значение коэффициента помехоустойчивости К_пз = 13,37 реализуется только в том случае, когда преднамеренная помеха также широкополосная и со спектром, ширина которого совпадает с шириной спектра широкополосного сигнала. Однако радиолиния не защищена, как и при работе с узкополосными сигналами, от сосредоточенных по спектру помех, когда ширина спектра преднамеренной помехи совпадает с шириной спектра информационного сигнала.

Далее сравним помехоустойчивость и помехозащищенность радиолиний управления, работающих с широкополосными и узкополосными ОФТ-сигналами, для чего ниже представлены полученные расчетные данные для узкополосной радиолинии.

Модель радиолинии, работающей с узкополосными ОФТ-сигналами, практически не отличается от модели широкополосной радиолинии, представленной на рис. 1 , разница лишь в том, что здесь полосовой фильтр Ф будет согласован с символом ОФТ-сигнала, а фильтр СФ в низкочастотном тракте будет отсутствовать.

Вероятность правильного приема символа ОФТ-сигнала в данном случае определяется по формуле

то коэффициент помехоустойчивости радиолинии, работающей с ОФТ-сигналами, составит 2,936.

При оценке коэффициента помехозащищенности радиолинии мы исходим из предположения, что ширину спектра преднамеренной помехи выбирает противник. Наибольший эффект при подавлении сигнала управления при этом достигается, когда ширина спектра преднамеренной шумовой помехи совпадает с шириной спектра сигнала. Следовательно, в случае ОФТ (т.е. узкополосного) сигнала получим

Кпз = Ку Jf = о, 73 7.

При этом следует иметь в виду, что приведенные выше данные для узкополосной радиолинии могут быть получены только при достаточно высоких требованиях к стабильности частоты радиосигнала, которую можно оценить следующим образом.

При уходе частоты сигнала от своего номинального значения на величину ∆ω₀ относительное изменение амплитуды видеосигнала составит

γ = ∆ V m = 1 - 1 ^T ∫ ^Э cos ( ∆ ω ₀ t ) d t = 1 - sin ( ω 0 T Э ) .   (22)

VmTЭ0                  ∆ω0TЭ

Определим требование к стабильности частоты сигнала, исходя из допустимого 5% снижения амплитуды видеосигнала

sin (o0T3) ^<»0 T3

> 0,95.

Из (23) следует

∆ f 0 ≤ 0 , 0 8 8

f 0      f 0 T Э

В нашем примере на частоте f₀ = 100 МГц получается

Р Э = 1 – 0.5 exp (–q²) ,

Δf 0 /f 0 ≤ 5,54 ×10^-8 .

где q² – отношение с/ш в полосе согласованного фильтра Ф .

Из (19) следует

Г 1"

q = ln--------. N 2(1-P3)

Стабильность частоты такого уровня в реальных условиях можно обеспечить лишь путем термостатирования опорного кварцевого генератора (что связано с резким увеличением потребляемого приемным прибором тока), которое в случае использования автономного питания приборов в большинстве случаев неприемлемо. Снижение требований к стабильности частоты возможно также при уменьшении длительности символа (увеличением разрядности кода), однако при этом соответственно будет

ухудшаться помехоустойчивость и помехозащищенность радиолинии.

Из сравнения полученных выше результатов легко видеть, что переход от узкополосной радиолинии, работающей с ОФТ-сигналами, к широкополосной радиолинии, работающей ОФТ-сигналами с линейной частотной модуляцией, сопровождается:

• ♦    резким увеличением коэффициента помехозащищенности, в нашем примере в 18,14 раз (от 0,737 до 13,37), что говорит о преимуществе такой радиолинии по сравнению с узкополосной при работе в условиях широкополосных помех;

• ♦    многократным снижением коэффициента помехоустойчивости, в нашем примере в 9,82 раза (от 2,936 до 0,299), что говорит о проигрыше широкополосной радиолинии узкополосной при работе в условиях узкополосных помех.

Приведенные данные позволяют видеть следующие основные недостатки рассмотренной широкополосной радиолинии:

• ♦    достаточно низкий коэффициент помехозащищенности радиолинии при воздействии сосредоточенной (т.е. узкополосной) помехи, что приведет к соответствующему снижению надежности приведения в действие исполнительных устройств в случае организованной постановки такого вида преднамеренных помех;

• ♦    существенное снижение коэффициента помехоустойчивости, что приведет к соответствующему снижению надежности приведения в действие исполнительных устройств в случае большой загрузки канала узкополосными помехами, в частности непреднамеренного характера;

• ♦    сложность формирования высокочастотного ОФТ-сиг-нала с линейной частотной модуляцией на передающей стороне и не меньшая сложность обработки сигнала на приемной стороне, что связано в основном с построением линии задержки на большое время задержки высокочастотного ЛЧМ-сигнала.

Выводы

Указанные недостатки могут сыграть решающую роль при определении целесообразности и технической приемлемости применения широкополосных ОФТ-сигналов с линейной частотной модуляцией в командных радиолиниях управления. В этом случае единственным достоинством широкополосной радиолинии является высокая скрытность сигналов управления, которая присуща всем системам, работающим с широкополосными сигналами, независимо от их структуры и особенностей технической реализации