Помехоустойчивость инвариантной системы передачи информации, основанной на когерентном приеме и при наличии слабых корреляционных связей

Инвариантные системы передачи информации могут базироваться на разных способах обработки информации, основанных на принципе относительной амплитудной модуляции. Этот принцип предполагает снижать действие мультипликативной помехи путем применения алгоритма частного информационного параметра к обучающему [1].

Авторами рассмотрены ранее четыре способа обработки сигналов с помощью инвариантной относительной амплитудной модуляции и различной коррелирован-ности отсчетов шума.

В работе [1] рассмотрена инвариантная относительная модуляция (ИОАМ) при идеальных условиях. В работе [2] рассмотрена инвариантная некогерентная система обработки информации. В работе [3] рассмотрены качественные характеристики ИОАМ при наличии помехи в генераторе. В работе [4] получены качественные характеристики ИОАМ в случае слабой коррелированности соседних отсчетов информационного и обучающего сигналов.

Постановка задачи. Имеем канал связи, ограниченный частотами fн и fв. Состояние канала связи определяет- ся интервалом стационарности, внутри которого действие мультипликативной помехи описывается постоянством коэффициента передачи сигнала k(t) на определенной частоте.

Мультипликативная помеха одинаково искажает информационные и обучающие части блока передаваемых сигналов. Однако отношение энергии информационного сигнала к энергии обучающего сигнала являются постоянными на интервале стационарности.

Помимо этого каждый передаваемый блок подвергается действию аддитивной помехи.

В данном исследовании предполагается, что ближайшие отсчеты аддитивной помехи слабо коррелированны между собой.

Необходимо произвести расчет вероятности попарного перехода инвариантов в рассматриваемой системе. Для этого необходимо найти аналитическое выражение плотности вероятности оценки инварианта.

Данная работа завершает исследование поведения ИОАМ при слабой коррелированности отсчетов информационного и обучающего сигналов.

Решение поставленной задачи. Структура приемной части инвариантной относительной амплитудной модуляции представлена на рис. 1. Такая структура содержит синхронный детектор (умножитель, ФАПЧ и ФНЧ) и спец-вычислитель.

На передающей стороне модулирующий параметр включен в отношение энергии информационного сигнала к энергии обучающего сигнала.

В силу того, что мультипликативная помеха одинаково воздействует на обе части каждого передаваемого блока, то алгоритм демодуляции сигналов приема, с учетом выбранного способа обработки сигналов, будет заключаться в вычислении оценки инварианта, описываемой следующим выражением:

N

Е ( к ■ INV + ^( i ))

^INV L =       -- ⁵ ОБ .      (1)

• 1    ЕЕ ( к ■ 5 ОБ + n( m , j ))

L j =1 m =1

В числителе выражения (1) представлена сумма N мгновенных отсчетов сигнала информационной посылки. Информационный сигнал образован прямоугольной огибающей с амплитудой к ■ INV l + ^( i ), где , ( i ) - отсчеты аддитивной помехи, распределенные по нормальному закону [5].

В знаменателе формулы (1) представлена сумма N мгновенных отсчетов сигнала обучающей посылки, образованного прямоугольной огибающей к ■ 5ОБ + n(m, j), где n(m, j) — помеха в m-й реализации обучающего сигнала, распределенная по нормальному закону [6].

Без ограничения общности полагаем, что 5 _ОБ = 1. Если 5 _ОБ * 1, то все исходные параметры, а именно INV l и с , (среднеквадратичное отклонение помехи , ( i ), n ( m , j )) можно масштабировать на величину 5 _ОБ. Тогда формула (1) с учетом введенных ограничений перепишется в виде

N

Е ( к ■ INV i + К i ))

INV * = —--------------= A ,      (2)

L NL

7 ЕЕ ^{( к} ■ ⁵ ОБ ⁺ n^{( m , j} ))

L j =1 m =1

где к ■ INV l - мгновенный отсчет сигнала информационной части посылки, поступающей из канала; , ( i ) - i -е мгновенное значение помехи в информационном сигнале; к - коэффициент передачи канала; n ( m , j ) - j -е мгновенное значение в m -й реализации обучающего сигнала.

Будем полагать, что случайные величины , ( i ) и n ( m , j ) одинаково распределены по нормальному закону с нулевым математическим ожиданием и дисперсией g , ². Кроме этого, предполагается, что в каждом блоке зависимы только соседние случайные величины. Тогда

CORR (,(i),,(i -1)) = CORR (n(m, j), n(m, j -1)) = R, где R - коэффициент корреляции.

Все остальные случайные величины, входящие в каждый принимаемый блок, будут независимыми. Для реализаций этой модели необходимо, чтобы [5]

I R | <  1/V2.

Воспользуемся известным подходом оценки вероятности попарного перехода, описанным, формулой полной вероятности

Zp                ∞

^Р пер = ^P 1 J w ⁽ z ) ^dz ⁺ P i J ^W 1 ⁽ z ) ^dz ^{,         (3)}

0                 Zp где Рпер - вероятность перехода INV1 в INVi и наборот; P1 -вероятность появления INV1; Pi - вероятность появления INVi. Первый интеграл - вероятность появления INVi, когда послан INV1. Второй интеграл - вероятность появления INV1, когда послан INV.; Zp - пороговое значение, необходимое для вычисления Pпер; при известных Р 1 и Pi оно определяется с помощью полученной байесовской оценки путем минимизации Рпер по Zp. При неизвестных Р 1 и Pi выбираем Р 1 = Р. = 0,5.

Из анализа (3) видно, что для вычисления Р _пе р необходимо знать аналитические выражения W 1 ( z ) и W ( z ) плотности вероятности оценки инварианта.

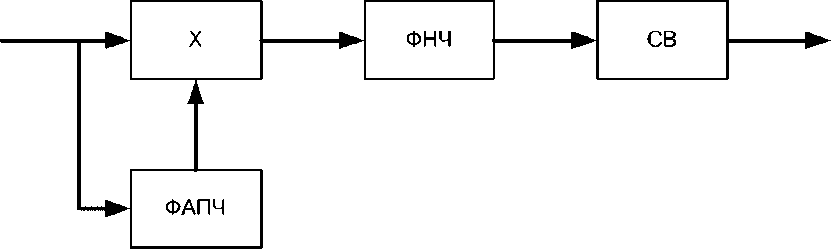
Рис. 1. Структурная схема инвариантной системы передачи информации: ФАПЧ - устройство фазовой автоподстройки частоты; ФНЧ - фильтр нижних частот; СВ - спецвычислитель

На основании выражения (2) вычислим математическое ожидание и дисперсию случайных величин А и В.

Математическое ожидание числителя будет равно [7]

m A = N ■ k ■ INVl.                   (4)

Математическое ожидание знаменателя будет равно [7]

m B = N ■ k.

Дисперсия числителя будет равна [7]

o A = D ( ^ ^( i )) = N ■ o + 2( N - 1)co<( i \ ^( i + 1)) =

= N ■ 02 + 2(N -1)R ■ 02 = o2(N + 2(N-1)R).(6)

Дисперсия знаменателя будет равна [7]:

oB = L 0(N + 2( N -1) R).(7)

Расчет частного двух случайных величин производится по следующей формуле [7]

„                _ ( zx - m A )² _ ( x - m B )²

W (z) =f----^-e   2oA ■ e 2oB Ixldx,(8)

-L 2no Ao B где уА и уB определяются выражениями (6) и (7); mA и mB определяются выражениями (4), (5).

Следует отметить, что в формуле (3) при расчете W ₁( z ) используется INV₁ и при расчете W_i ( z ) – INV _i , где i = 2, 3, 4, 5, 6, 7. Значение вероятности попарного перехода Р _пер находилось методом численного интегрирования. Число накоплений с усреднениями равно 40 [1].

Полученные данные ограничены первыми шестью парами сравниваемых инвариантов, когда INV₁ = 1, INV _i = 2, 3, 4, 5, 6, 7.

Вероятность попарного перехода вычисляется при значениях h – отношения «сигнал/шум», которое находилось по формуле, определяемой отношением мощности сигнала и мощности шума [6]

• 2    k ²INV _l ² h =----B—.

N σ_ξ²

Пороговые значения Z_p отыскивались минимизацией Р _пер в формуле (3).

Результаты расчетов для различных значений коэффициента передачи канала k , коэффициента корреляции R и величины INV ₁ = 1; INV _i = 2; 3; 4; 5; 6; 7 сведены в табл. 1, 2.

Если в формулах (6) и (7) положить R = 0 (отсчеты шума некоррелированы), то общее выражение плотности вероятности оценки инварианта, полученное в данной работе, переходит в соотношение по расчету аналогичного параметра, полученного авторами ранее при действии некоррелированных отсчетов белого шума [1]. Однако полученное выражение плотности в данной работе является уточняющим и наиболее полно отражает реаль- ную ситуацию.

Особенностью любой инвариантной системы, основанной на принципе инвариантной относительной амплитудной модуляции является то, что по каналу передаются амплитудно-модулированные сигналы, образованные INV _l и S _ОБ.

Передача этих сигналов обеспечивается на основе классических алгоритмов обработки информации и имеет невысокую помехоустойчивость.

Кривая 3 на рис. 2 и рис. 3 соответствует вероятности ошибки Р _ош, является аналогом вероятности попарного переход Р _пер и рассчитывается по известным формулам [5] и только после обработки этих сигналов в соответствии с алгоритмом частного по выражению (1), получаем оценку инварианта, по сути являющуюся числом, а не сигналом.

Как видно, вероятность попарного перехода в инвариантной системе определяется величинами (10–1…10–33) (рис. 2, 3). При тех же значениях «сигнал/шум» вероятность ошибочного приема единичного символа в классических системах лежит в пределах (10–1…10–7).

1     2    3    4    5    6    7

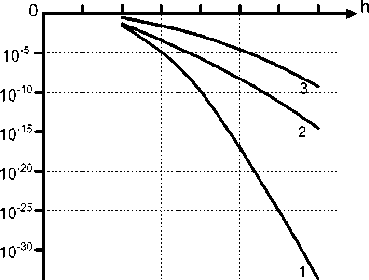
10'35.

Pom' '

Рис. 2. Помехоустойчивость ИОАМ при k = 1 и INV₁ = 1;

INV _i = 2; 3; 4; 5; 6; 7: кривая 1 – вероятность попарного перехода в ИОАМ при некоррелированности отсчетов шума (теоретический предел); кривая 2 – вероятность попарного перехода ИОАМ при R = 0,7; кривая 3 – вероятность ошибки классической АМ

Проведенный анализ инвариантной системы показывает, что инвариантная система передачи информации при слабой корреляции отсчетов аддитивной помехи обладает в ысокой помехоустойчивостью. Вероятность ошибки классического алгоритма с амплитудной модуляцией как минимум на два порядка больше вероятности попарного перехода в инвариантной системе. Поэтому данную систему следует использовать в телекоммуникационных системах, системах телеуправления и других

Таблица 1

Значения Z p при заданных K , R

K = 1				R = 0,7
Z p	1,627	2,057	2,488	3,062	3,516	4,162

Таблица 2

Значения Z p при заданных K , R

K = 0,7 R = 0,7 Zp 1,820 2,226 2,632 3,038 3,646 4,078 системах, предъявляющих высокие требования к помехоустойчивости.

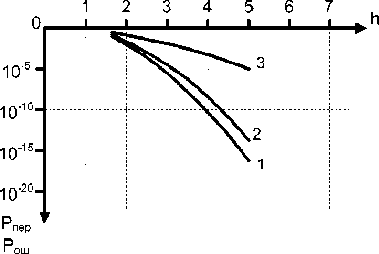
Рис. 3. Помехоустойчивость ИОАМ при k = 0,7 и INV₁ = 1;

INV _i = 2; 3; 4; 5; 6; 7: кривая 1 – вероятность попарного перехода в ИОАМ при некоррелированности отсчетов шума (теоретический предел); кривая 2 – вероятность попарного перехода ИОАМ при R = 0,7; кривая 3 – вероятность ошибки классической АМ