Помехоустойчивость канала передачи данных с ППРЧ при мягком декодировании с использованием оценок спектральной плотности мощности помехи

В каналах передачи данных с псевдослучайной перестройкой рабочей частоты (ППРЧ) часто используется каскадное кодирование, на внутренней ступени которого применяется ансамбль ортогональных сигналов, а на внешней – код Рида-Соломона (РС) [1]. В [2, 3] получены математические выражения для квазиоптимальных оценок спектральной плотности мощности шумовой помехи, формируемых по наблюдению выходов когерентного и некогерентного многоканальных устройств различения ортогональных сигналов. Такие оценки необходимы для реализации близкой к потенциальной помехоустойчивости канала за счет мягкого декодирования РС-кода.

Доказано [4], что при ППРЧ с большим числом рабочих частот наихудшая помеха в каждый момент времени равномерно выбирает часть из них, на которую действует с одним превышением, а на оставшуюся часть – с другим. Такая помеха может быть представлена как смесь двух помех – заградительной и сосредоточенной в части полосы ППРЧ [5]. Первая помеха для приемника имеет непрерывный характер, вторая – импульсный [6–8]. Для условий действия – 844 – непрерывной и наихудшей импульсной помех в [9] исследована помехоустойчивость когерентного канала передачи данных с ортогональными сигналами и РС-кодом при его жестком декодировании.

Цель работы - получить характеристики помехоустойчивости когерентного канала передачи данных с ППРЧ, ортогональными сигналами и РС-кодом при его мягком декодировании с использованием оценок спектральной плотности мощности помехи, представляющей совокупность двух гауссовских шумовых помех – заградительной и сосредоточенной в части полосы ППРЧ.

Описание канала передачи данных

По каналу передаются блоки кода РС ( n,k ). Каждый из n символов блока кода передается на своей частоте, выбранной по псевдослучайному закону. С вероятностью р выбранная частота находится под воздействием помехи, сосредоточенной в ρ-й части полосы ППРЧ, 0 < ρ ≤ 1. Такая помеха со значением р = р * , максимизирующим требуемое для обеспечения заданной достоверности отношение сигнал/помеха, является наихудшей [10, 11].

Для передачи каждого i -го, , символа блока используется один из М ортогональных равноэнергетических сигналов (априорные вероятности передачи каждого из М сигналов равны). Прием блока кода осуществляется на временном отрезке [0, nT ], где Т -длительность символа.

На входе демодулятора (многоканального устройства различения ортогональных сигналов) приемника при (i - 1) T <  t <  iT действует наблюдение

5(t) = sj(t) + n (tX где n(t) - белый гауссовский шум (БГШ) со спектральной плотностью N, неизвестной приемнику.

В соответствии с целью работы n (t) = n o(t) + 5 in i(t), где n0(t) - модель заградительной помехи в виде БГШ со спектральной плотностью N0; 5in ^(t) -модель помехи, сосредоточенной в части полосы ППРЧ; 5i - дискретная случайная величина, принимающая два возможных значения: 1 с вероятностью ρ, 0 с вероятностью (1 – ρ); n\(t) - БГШ со спектральной плотностью N1 / р, где N1 - средняя спектральная плотность мощности помехи, сосредоточенной в части полосы ППРЧ.

При приеме каждого i -го символа блока кода в каждом из М каналов демодулятора формируются корреляционные интегралы

%„ =  ! 5UY4_mVVil. m = l.M .

(Mr

Решение /_; о том, какой из М сигналов (символов) был передан на интервале ( i - 1) T < t <  iT, формируется по максимуму корреляционного интеграла. Для сформированного решения вычисляют оценку его апостериорной вероятности. В соответствии с известным выражением для апостериорной вероятности [12] ее оценка формируется следующим образом:

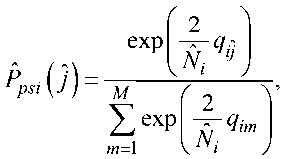
где Nj - оценка неизвестной спектральной плотности помехи n(t), сформированная на интервале (i - 1) T <  t <  iT.

Совокупность решения i_t и оценки P_psj ( /) его апостериорной вероятности является мягким решением [13, 14].

Для вычисления оценки апостериорной вероятности используется квазиоптимальная (по максимуму правдоподобия) оценка спектральной плотности помехи [2, 3]

,

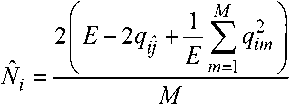
т где              – энергия сигнала.

о

Последовательность из n мягких решений декодируется по алгоритму, основанному на алгоритме минимального обобщенного расстояния (МОР) [13]: в соответствии с алгоритмом МОР порождается небольшое множество кодовых слов, из порожденного множества в качестве решения выбирается кодовое слово, наиболее близкое по Хеммингу к последовательности решений /у.

Методика получения характеристик помехоустойчивости

Характеристики помехоустойчивости были получены имитационным компьютерным моделированием на основе соотношения для вероятности неправильного декодирования блока

РН.БЛ. = P1 + (1 — P1) • P2, где P1 - вероятность того, что в порожденном множестве нет переданного кодового слова; P2 -вероятность того, что переданное кодовое слово не будет выбрано в качестве решения при условии, что в порожденном множестве оно есть.

Вероятность P ₂ для исследуемых кодов пренебрежимо мала по сравнению с P 1 [14, 15]. P 1 оценивается с помощью достаточно простого моделирования, не требующего реализации наиболее сложных функций кодера и декодера. Моделируется только блок сортировки символов, обеспечивающий упорядочение последовательности решений в соответствии с их апостериорными вероятностями. После сортировки анализируется количество ошибок в наиболее достоверных (нестертых) k, k+2, … , n решениях. Если хотя бы в одной из таких последовательностей упорядоченных решений количество ошибок не более количества исправляемых (например, при k+2 допустима одна ошибка), декодирование блока будет правильным.

Для моделирования потребовалась нормировка показателей экспонент в (1). Эта операция позволила задавать математические ожидания и дисперсии генерируемых при моделировании – 846 – корреляционных интегралов через отношения сигнал/помеха Q0 = 2E / N0 и Q1 = 2E / N1. Нормировка была выполнена следующим образом:

,

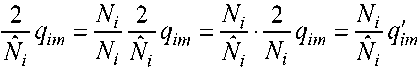
где 4im грал.

2                       „                                           „                    „

^—   9 ini – формируемый при моделировании нормированный корреляционный инте-

Nj

При моделировании приема на частоте, пораженной помехой в части полосы ППРЧ, дисперсии нормированных корреляционных интегралов всех М каналов приема равны математиче- скому ожиданию нормированного корреляционного интеграла согласованного канала и равны

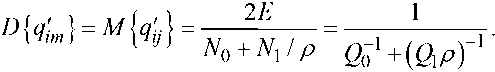
Для остальных каналов, кроме согласованного, математическое ожидание равно нулю.

При моделировании приема на частоте, не пораженной помехой в части полосы ППРЧ, для канала, согласованного с принимаемым сигналом, M^ = Q₀ (для остальных каналов математическое ожидание равно нулю). Для всех каналов WlmbSo .

Результаты компьютерного моделирования

По результатам моделирования определяли отношение з=<е_ь^4;_в , где N 10 = N 0 + N 1 , энергии сигнала, приходящейся на один бит передаваемой информации, к спектральной плотности суммарной помехи, требуемое для обеспечения вероятности ошибки в бите 10 ^-4 . По минимуму этого параметра для наихудшей помехи аналогично [16] были определены оптимальные РС-коды, представленные в табл. 1.

Характеристики помехоустойчивости канала передачи данных при применении опти-

Таблица 1. Оптимальные РС-коды

Table 1. Optimal PC codes

M (Eb / N0)dB 5 10 15 32 (31,19) (31,15) (31,13) 64 (63,39) (63,33) (63,31) 128 (127,79) (127,69) (127,67) мальных РС-кодов представлены на рис. 1–3.

Характеристики показывают существенный выигрыш мягкого декодирования (МД) относительно жесткого (ЖД) как по требуемому отношению сигнал/помеха, так и по граничному значению ρ гр параметра ρ: при ρ <ρ гр требуемая достоверность достигается независимо от мощности помехи. Для оптимальных РС-кодов (табл. 1) сравнение ρ_гр приведено в табл. 2.

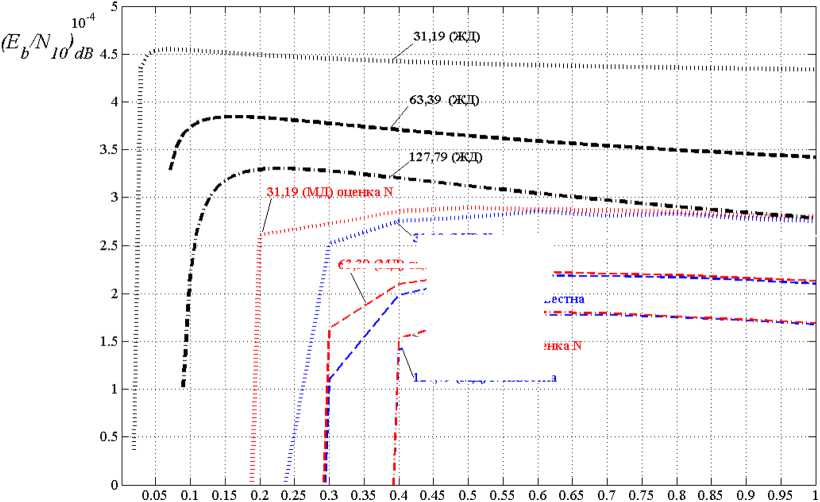
31,19 (МД) N известна

63,39 (МД) оценка N;     ;___■ _

' 63.39 (МД)Хтв

Рис. 1. Помехоустойчивость канала передачи данных при ( E b / N 0 ) dB = 5 dB

J-"'^'.12'79 (M.l) 6ц

127,79 (МД) N известна

Fig. 1. Noise immunity of the data transmission channel at ( E b / N 0 ) dB = 5 dB

О О.О5 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95   1

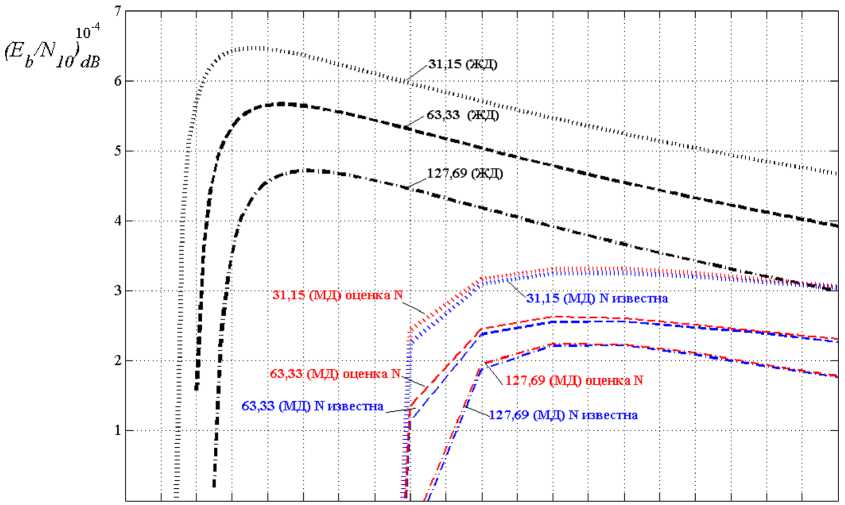
Рис. 2. Помехоустойчивость канала передачи данных при ( E b / N 0 ) dB = 10 dB

Fig. 2. Noise immunity of the data transmission channel at ( E b / N 0 ) dB = 10 dB

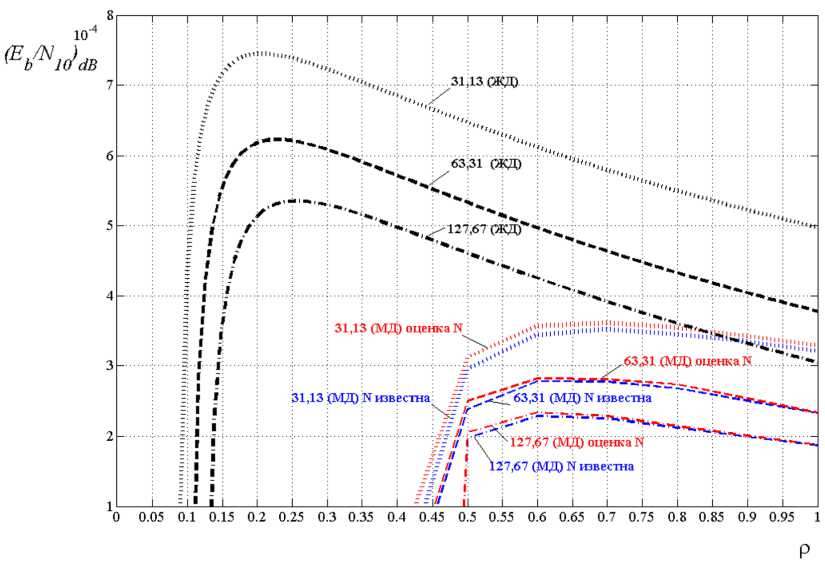
Рис. 3. Помехоустойчивость канала передачи данных при ( E b / N 0 ) dB = 15 dB

Fig. 3. Noise immunity of the data transmission channel at ( E b / N 0 ) dB = 15 dB

Таблица 2. Сравнение ρ гр для оптимальных РС-кодов

Table 2. Comparison of ρгр for optimal PC codes

М		( Eb / N 0) dB
		5	10	15
32	МД	0,29	0,34	0,35
	ЖД	0,02	0,06	0,08
64	МД	0,27	0,37	0,40
	ЖД	0,05	0,09	0,10
128	МД	0,32	0,40	0,41
	ЖД	0,08	0,11	0,12

Для более точного сопоставления помехоустойчивости канала передачи данных при МД с известной спектральной плотностью N_i и неизвестной, когда формируется и используется ее оценка N^ , на рис. 4–6 соответствующие характеристики представлены отдельно.

Из сравнения кривых видно, что при увеличении М помехоустойчивость канала передачи данных при МД с неизвестной спектральной плотностью помехи, когда формируется и используется ее оценка N^ , приближается к помехоустойчивости при известной спектральной плотности N_i , являющейся потенциальной для МД. Для количественной оценки приближения к потенциальным характеристикам были использованы среднеквадратическая мера

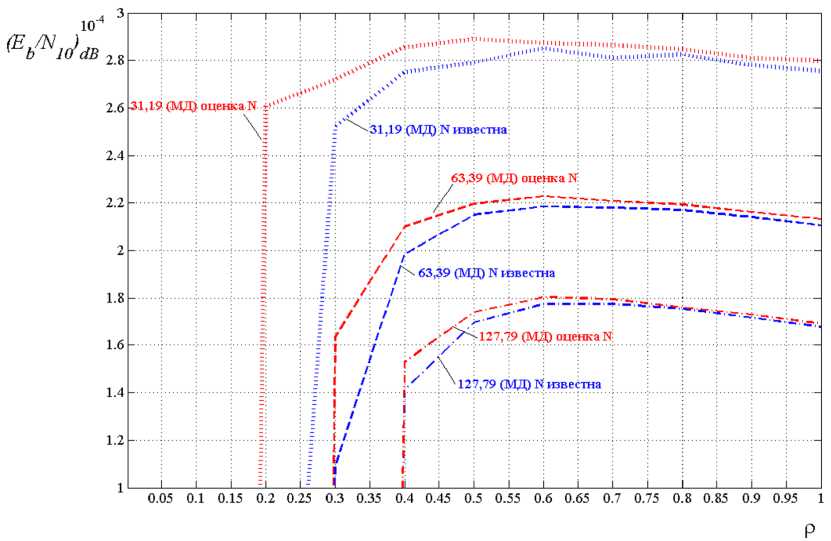
Рис. 4. Помехоустойчивость канала передачи данных при ( E_b / N ₀) _dB = 5 dB при мягком декодировании

Fig. 4. Noise immunity of the data transmission channel at ( E b / N 0 ) dB = 5 dB with soft decoding

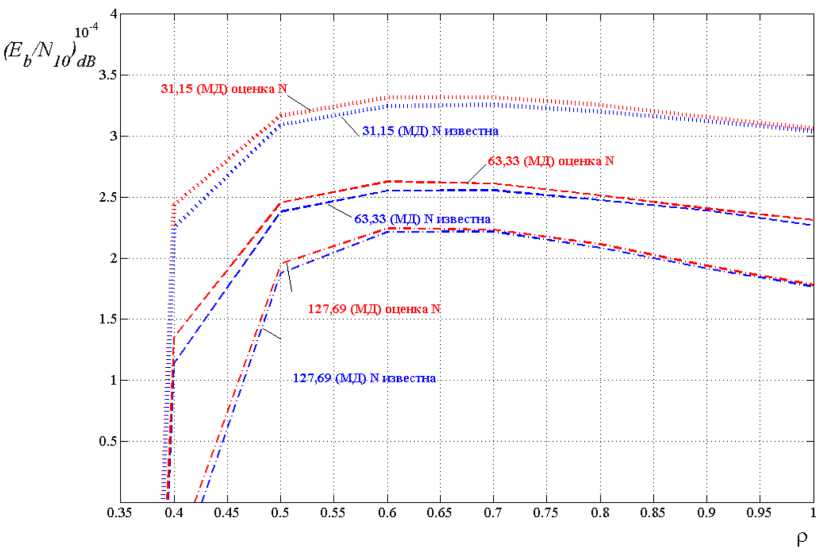
Рис. 5. Помехоустойчивость канала передачи данных при ( E_b / N ₀) _dB = 10 dB при мягком декодировании

Fig. 5. Noise immunity of the data transmission channel at ( E b / N 0 ) dB = 10 dB with soft decoding

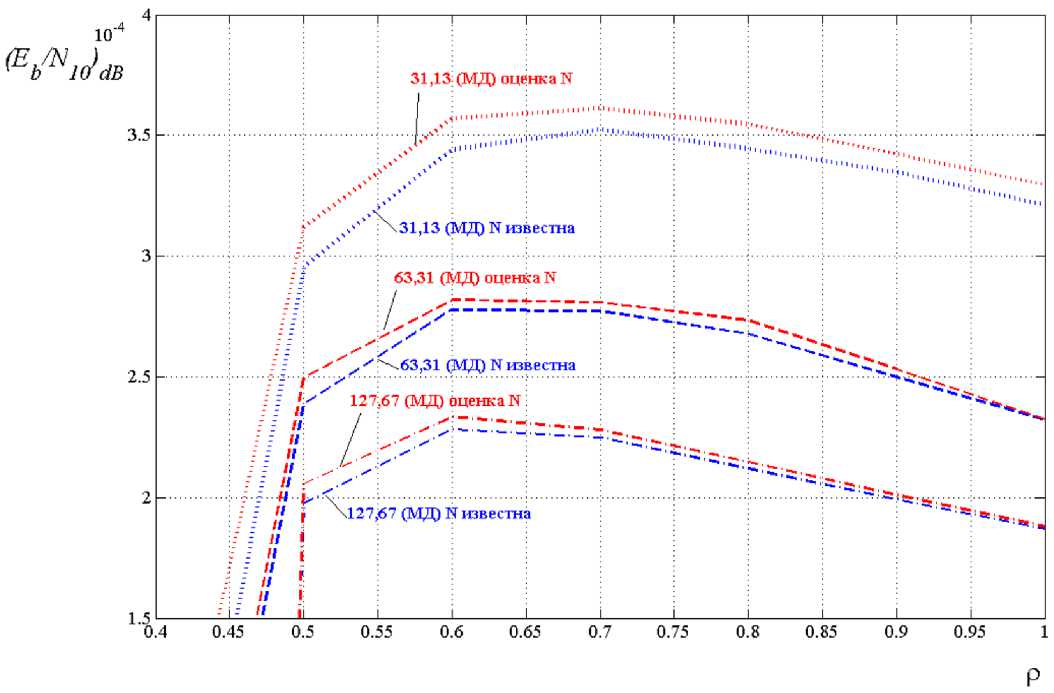
Рис. 6. Помехоустойчивость канала передачи данных при ( E_b / N ₀) _dB = 15 dB при мягком декодировании

Fig. 6. Noise immunity of the data transmission channel at ( E b / N 0 ) dB = 15 dB with soft decoding

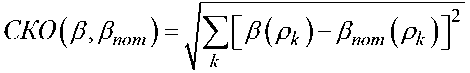
и мера Кульбака [12], имеющая с учетом того, что β измеряется в децибелах, следующий вид:

A'

Мера Кульбака в отличие от среднеквадратической меры подчеркивает важность «хвостов» распределения, придает им большую значимость, что очень существенно для учета различий характеристик помехоустойчивости в области ρгр.

Результаты расчетов среднеквадратической меры представлены в табл. 2, меры Кульбака – в табл. 3.

Таблица 3. Среднеквадратическая мера

Table 3. Root-mean-square measure

M	( E b / N 0 ) dB
	5	10	15
32	1,28	0,07	0,19
64	0,18	0,08	0,07
128	0,04	0,06	0,03

Таблица 4. Мера Кульбака

Table 4. Kulbak's measure

M	( E b / N 0 ) dB
	5	10	15
32	0,85	0,1	0,2
64	0,13	0,08	0,07
128	0,03	0,05	0,04

Заключение

Таким образом, полученные результаты исследования помехоустойчивости канала передачи данных с ППРЧ при мягком декодировании с использованием оценок спектральной плотности мощности помехи показали, что при увеличении объема ансамбля ортогональных сигналов помехоустойчивость повышается за счет повышения точности оценки спектральной плотности мощности помехи, что в свою очередь обеспечивает повышение точности оценки апостериорной вероятности, используемой при декодировании мягких решений. Это является дополнительным к известным положениям обоснованием целесообразности увеличения объема ансамбля ортогональных сигналов.