Помехоустойчивость поиска широкополосных сигналов с минимальным сдвигом частотной манипуляции радионавигационной системы при воздействии структурных помех

В радионавигационных системах (РНС) с широкополосными сигналами (ШПС) возможно воздействие взаимных и структурных помех, которые представляют собой ШПС такого же типа, что и используемые в широкополосных РНС – сигналы, излучённые опорными станциями (ОС) [1]. Приём сигнала бортовой станцией (БС) РНС может осуществляться в условиях воздействия помех в виде мешающих сигналов: сигналов поверхностных волн других ОС и сигналов пространственных волн тех ОС, которые удалены от БС на расстояния не менее 100 км с учётом рабочих частот. Для РНС «Спрут» с рабочей частотой ≃ 2 МГц на расстояниях до 1000 км воздействием пространственной волны можно пренебречь [2], тогда для РНС

«Спрут» с тремя опорными станциями число мешающих сигналов относительно приёма БС составит не более двух.

При использовании в качестве модулирующих псевдослучайных последовательностей циклические сдвиги кода, общего для всех опорных станций, показанные мешающие сигналы могут рассматриваться как помехи в виде копий полезного сигнала, циклически сдвинутые по времени. Когда в точке приёма БС мощности излучённых сигналов ОС приблизительно равновелики, то такие мешающие сигналы можно отнести ко взаимным помехам и анализ необходимого сигнала возможен на основе обычного кодового разделения [3]. В случае, когда мощность P_s анализируемого сигнала существенно меньше мощности P n мешающего сигнала ( K - 20 - 30 аА , K = 10 Lg ( P n I P s ) - интенсивность помехи), ОС мешающего сигнала расположена существенно ближе к БС, чем ОС анализируемого сигнала), то мешающий сигнал представляет собой структурную помеху (СП). Воздействие мощных структурных помех в форме широкополосных сигналов с ФМ на анализируемый ФМ сигнал подробно исследовано в работе [4].

В рассматриваемой РНС «Спрут» опорные станции расположены в вершинах равностороннего треугольника со стороной 300–400 км. Каждая из ОС излучает ШПС с частотной манипуляцией при минимальном сдвиге (ЧММС) [5], у которого модулирующий код { d_nl } представляет собой циклически сдвинутую на n элементов исходную M -кодовую последовательность. При распространении сигналов между ОС над поверхностью моря на расстояние до 350 км происходит подавление сигнала на 34 дБ [2]. Отсюда мощность сигнала, излучаемого ближайшей ОС для БС будет превышать мощность сигнала, излучаемого от наиболее удалённой ОС для той же БС на 34 дБ. В этом случае сигнал s_п ( t ) с наибольшей мощностью P_n , отличающейся от мощности P_s полезного сигнала s ( t ) на величину K интенсивности помехи, будет представлять собой структурную помеху s_п ( t ) . Воздействие структурной помехи при поиске широкополосного сигнала с ЧММС на сегодня в литературе отсутствует, что явилось побудительным мотивом для анализа воздействия структурных помех на поиск ШПС – ЧММС сигналов опорных станций наземной РНС, позволяющего в значительной степени снизить влияние структурных помех на «поиск» широкополосных сигналов с ЧММС.

Помехоустойчивость параллельного поиска ШПС – ЧММС

Исполним алгоритм параллельного поиска [6] в форме выполнения оптимальной процедуры обнаружения и распознавания одного из L сигналов, отличающихся временным циклическим сдвигом т k = ( к - 1) т э ( к = 1, L , L - длина модулирующей кодовой последовательности, т э - длительность элемента сигнала или элемента модулирующей кодовой последовательности { d_kl } ) [7]. Для оценки помехоустойчивости используем в качестве критерия вероятность правильного определения номера квадратурного коррелятора (КК), на выходе которого вычисленный модуль V_k корреляции анализируемого и опорного сигналов окажется наибольшим среди L - 1 значений. Отсюда вероятность правильного распознавания сигнала будет иметь место, если из всех значений модулей V 1 ,V ₂,..., V_L - 1 наибольшим окажется V_k . Следовательно, вероятность Р _пр правильного распознавания сигнала есть вероятность того, что если V k = V max , то все остальные L- 1 значения ( V 1 ,V 2 ,...,V L , кроме V_k ) меньше V _max , т. е. вероятность Р пр соответствует значению функции распределения модуля V k на интервале [0, +~ ] при плотности распределения f ( V_k ) модуля V_k :

то

Р пр = Р(V k = V max ) = J ₀ f (V k ) dV k .                            (1)

Плотность распределения f ( V_k ) модуля V k корреляции можно выразить через L - 1 кратное интегрирование L -мерной плотности вероятности модулей V 1 ,..., V_L - W ( V ) [8]:

Vk Vk f (Vk) = J ... J W(V)dV1... dVl ... dVL .

0 0              l * k

При действии флуктуационной помехи совместно с сигналом на входы L квадратурных корреляторов значения V1,V2,...,VL будут являться функциями от ортогональных сигналов. Можно сказать, что каждый из модулей будет являться независимой случайной величиной и тогда распределение W(V) можно выразить через произведение распределений независимых случайных величин (модулей) V1,...,VL . С учётом поведения основного выброса модуля норми- рованной периодической автокорреляционной функции (НПАКФ) [5] широкополосного сигна- ла при ЧММС

R (т) = ^

1 -

)

2 L э J cos

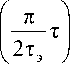
+—Sin π

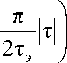
I^T ^ 2^T э

0,

|T| > 2Tэ.

L -мерную плотность вероятности W ( V ) можно выразить через произведение:

– одномерной плотности W ₁ ( V_k ) на выходе синхронного квадратурного коррелятора (где опорный сигнал по форме соответствует анализируемому сигналу) по закону Рэлея – Райса при 2

квадрате математического ожидания M ( V k ) = ET /2 ( E = AT /2 - энергия сигнала, A - амплитуда сигнала,

T = L т_э - длительность сигнала) и дисперсии а² = D ( V ) = N o T / 4 модуля V k [7]

W i ( V k ) =

V k

D ( V )

<77 Л

^Vk ^{+ M} 2 ⁽ Vk )

2 D ( V )

e ^{V            J}

I o

( V_k M V ) ) = V k I УР У ) e- ^{(Vk /}^) - h ² I

( D ( V ) J    7D V )                o

₂   ^V k   _h

D ( V )

где I 0 ( * ) - модифицированная функция Бесселя нулевого порядка [9], 2 h ² = M ²( V )/ D ( V ) = ( ET /2)/( N o T 14) - отношение Сигнал/ Шум на выходе КК при оптимальной корреляционной обработке сигналов в k -м квадратурном корреляторе;

– двух одномерных плотностей распределения модулей V _τ на выходах соседних (относительно синхронного) в k + 1 -м и k - 1 -м квадратурных корреляторах (код модуляции в опорных сигналах сдвинут на ± т _э ) по закону Рэлея - Райса при квадрате математического ожидания 22

M ( V _T ) = PTR (т _э )/2 ( с учётом НПАКФ (3)) и дисперсии а = D ( V ) квадратурных составляющих модуля V _т с подстановкой u = V k ² /2 D ( V ) получим

2 л ^Vk ^-

W ₂ ( V ) = П--- [Ve

^{2 T} | = | D ( V ) J ^т

V ² + M ²( V т) R ²(т э )

2 D ( V )

V τ M ( V τ ) R (τ э )

D ( V )

dV _т =

' _ V l

² W) I o [ 2 hR (т _э )V U ]

e [ u + h ² R ²( т э )]

du

; (5)

- одномерных распределений W (Vl) на выходах остальных L - 3 квадратурных коррелято рах по закону Рэлея при дисперсии а2 = D(V)

L - 3    1 ^Vk

W 3 ( V ) = П---- [V/e ^{3 l}   У D ( V ) ^{J l}

Vl

2 D ( V )

V

у

L - 3 ^Vk ^{2/2D( V} ) ^dV i = n J

I = 1      0

^Vk ²

e" x dx = (1 - e ^{2D( V} ) ) L ^{- 3}

.

Введя обозначения р = V_k I а, u = V _т / а и интегрируя L - 3 кратное распределение Рэлея (5) по V_l / σ многомерное распределение W ( V ) для (2) запишем в следующей форме:

W ( V ) = W i (V_k )W 2 (V k ) W 3 ( V k ) =

V k D ( V ) D ( V )

I ( 2    ^{V k}    h )

^o      D ( V )

( Vk I VD y ) ² + h 2 e ²

V _k ²

2 D ( V )

J

Io (2hR(τэ) u) du e (u+h 2 R 2(т э))

~ ""I L —3 ^k

1 - e ^{2D( V} )

.

Тогда вероятность правильного обнаружения максимального модуля V_k квадратурным коррелятором с номером k при анализе принятого сигнала, с учётом (1)–(7) и замены переменных р ^{- 2}12 ^ р будет определяться как

_ ^J I o ^[ 2 Vp h ] ’"= i "FT"

ρ

J

Io [2 JuhR(тэ)] ] r

_{2 2} n ^] du Г 1 - e "^P ] d P .

u+h2R2(тэ) I             LJ eL            ]

Формула (8) используется в предположении, что эквивалентная циклическая задержка τ _l анализируемого сигнала может принимать значения, кратные 0,1т_э, 2т_э,...,( L- 1)т_э. В этом случае анализируемый и опорные сигналы синхронны относительно времени с точностью до τ_э и по завершению поиска устанавливается идеальная кодовая синхронизация. Временные диаграммы, поясняющие синхронность анализируемого и опорного сигналов, приведены на рис. 1. В последнем случае, когда моменты t_p (начало p элемента анализируемого сигнала s_r ( t )) и t_o (начало действия опорного сигнала s_o ( t ) или обработки s_r ( t ) сигнала) должны совпадать, то должно выполняться тождество t p = t ₀ (рис. 1). Этому соответствует нулевая временная отстройка т = t p - t ₀ = 0 опорного сигнала «синхронного» квадратурного канала относительно анализируемого сигнала (значение модуля V_k будет соответствовать максимуму НПАКФ, рис. 1, в ). Хотя вероятность такой «синхронности» практически равна нулю, но при имитационном моделировании можно задать условие t p = t ₀ и определить вероятность ошибки синхронизации при заданном отношении Сигнал/ Шум. С учётом (8) вероятность ошибочного обнаружения максимального значения модуля квадратурным коррелятором с номером l ^ k будет ^р о = ^{1 - р} пр .

При т = 0 выходу V_k квадратурного коррелятора с номером k соответствует максимальная вероятность правильного распознавания Р _пр|т = ₀ = P(V_k >  V l ), l = 1, L - 1, l ^ k , которой соответствует вероятность ошибочного обнаружения

J

P o = ¹ - J

I o [ 2VP h ] p ⁺ h ^{2 ]} e ^{L     ]}

ρ

J

Io [2 JuhR (тэ)] ] r

Г _{2 2} и ^] du [ 1 - e "^P ] d P •

I u+h2R2(тэ )l             LJ eL            ]

В случае, когда ошибка синхронизации т может оказаться равной значению ± тэ 12 - это наименее благоприятный случай и по завершении «поиска» погрешность кодовой синхронизации может составить ± тэ. В этом случае выходы Vk-1, Vk и Vk+1 квадратурных корреляторов (с номерами k -1, k и k +1), при опорных сигналах с соответствующими временными отстройками тэ 12 , -тэ 12 и -3тэ 12 относительно анализируемого сигнала, определяются соот- ветственно значениями основного выброса НПАКФ (3) как R(-тэ /2), R(тэ /2) и R(3тэ /2). При этом вероятность ошибки распознавания можно определить посредством учёта в распределениях W1(p), W21(p) и W22(p) значений НПАКФ R(тэ /2), R(-тэ /2) и R(3тэ /2) соответственно. В силу чётности НПАКФ (3) относительно τ распределения W1 (ρ) и W2.1 (ρ) будут совпадать по форме. При «поиске» с момента to ошибке синхронизации соответствует значение т = to - tp . Момент to относительно момента tp (временной координаты максимума основного выброса НПАКФ сигнала) можно рассматривать как случайную величину, распределённую равномерно на интервале [- тэ /2,+тэ /2]. В этом случае условные вероятности правильного обнаружения при временной отстройке т = + тэ /2 и при временной отстройке т = -тэ / 2 (в силу чётности НПАКФ относительно τ ) будут одного значения. Тогда полная условная вероятность правильного обнаружения будет определяться через удвоение и условная вероятность ошибочного обнаружения максимального модуля квадратурным коррелятором с номером к при «поиске» с конечным значении временной отстройки т = |тэ / 2| принимает следующий вид:

^P 0.5τ _э

= 1 -

то

2J

I o ( 2TP hR (т э /2) ) ( р + h ² R ²( т _э /2) ) e

р I o ( 2 VUhR ( - т _э /2 )

^J       ( u + h ² R ²( - т _э /2) )

0 e

^р I o ( ²^ hR (Зт э /2 )

J      ( u + h 2 R 2 .3т э /2) )    d^{U ( 1 -} e

0 e                      _

L - 3

■ ^-р )      d р.

а )

s_r ( t )

^ г + 1 ⁽ t )

iii

^p i _{t p}

p +1 i i i

L -1

L

iii

б )

[V T )

в )

^p i _{t 0}

i     i R ( T )   [

\ ।    i R ( Т э )

I     I >I\ T p

p +1 i _{t 1}

i i i L -1

L

0 т    2т   3т э        ээ

R (-Т э )

iii p-1 p i i i

I R (-Т э + т )

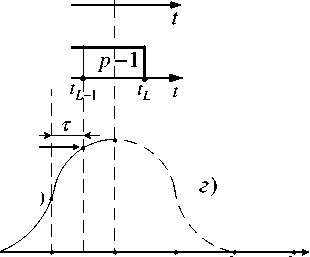
t

( L - 2) т _э ( L - 1) т _э Lт _э

T 2т  3т э ээ

Рис. 1. Эпюры анализируемого s_r ( t ) и опорного s ₀ ( t ) сигналов

Fig. 1. Time diagrams of analyzed s_r ( t ) and comparison s ₀ ( t ) signals

Формулы (9) и (10) определяют вероятность ошибки в двух крайних случаях: ошибка синхронизации т = 0 и |т| = т_э /2 соответственно. Учитывая случайный характер параметра т , целесообразно определить среднее значение вероятности ошибки, полагая случайную величину τ равномерно распределённой на интервале [ - т_э /2, + т_э / 2]:

2 т э 7 I o [ ² Ур ^{hR (т)} ] ср ' ^- т э i ^J 0 e [-+ h ² R ² 'I

p I_o |^2 4uhR (т + т _э ) ]

^J       e [ u + h ² R ²(т + т э ) ]

du

P. I o [ 2 4uhR (т - т э ) ]

^J        [ u + h ² R ²(т - т э ) ]

du

L - 3

||1 - e P ]    dp

d τ

На рис. 2. представлены графики зависимости вероятности ошибки P _o, Р _ср, P _{o 5 т} э от отношения Сигнал/ Шум h ² при L = 2¹⁴ - 1 = 16383, рассчитанные по формулам (9)-(11). График 1

построен для вероятности P_o и соответствует синхронному поиску при отсутствии ошибки синхронизации (т = 0). График 2 построен для средней вероятности ошибки Р ср и соответствует «поиску» при возможной случайной временной ошибке равномерно распределённой на интервале [ - т_э /2, + т_э /2]. График 3 построен для вероятности Р ₀ . _5т э при «поиске» с ошибкой |т| = т_э /2 синхронизации. Согласно рис. 2 (графики 2-3) с практической целесообразностью наиболее приемлемо проводить поиск с вероятностью ошибки не хуже 1*10^–3 при отношении Сигнал/ Шум h ² = 15 ^ 16 дБ.

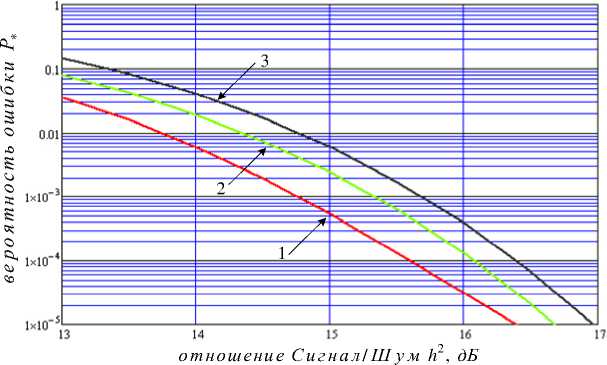
Рис. 2. Зависимости вероятности ошибки от отношения Сигнал/ Шум

1 - т = 0; 2 - {т} = (-т э /2,+т э /2); 3 - |т| = т э /2

Fig. 2. Dependence of the error probability on the Signal-to-Noise ratio

1 - т = 0; 2 - {т} = (-т э /2,+т э /2); 3 - |т| = т э /2

Метод расчёта энергетических потерь анализируемого сигнала при действии СП

Помехозащищённость алгоритма поиска бортовой станции сигнала s ( t ) при совместном воздействии структурной s_n ( t ) и флуктуационной помехи ξ( t ) исследуем посредством схемы оптимального двоичного распознавания ортогональных сигналов с неизвестной фазой.

Как известно [7], распознавание одного из двух дискретных сигналов (модулирующий код каждого из сигналов отличается на такой циклический сдвиг n _min , при котором коэффициент взаимной корреляции R mi _n( n _min т э ) равен минимальной величине R min = 1/ L ) со случайной фазой в присутствии флуктуационной помехи производится посредством схемы, приведенной на рис. 3.

Схема распознавания включает в себя две пары синфазных и квадратурных корреляторов K_i и K q действующих на едином временном интервале {t } = 0, T ( T = т_э L ):

– для вычисления составляющих Y_k и Y ^ˆ _k модуля V_k корреляции принятой реализации в форме s ( t ) + s n ( t ) + ^( t ) и опорного сигнала s o k ( t ), вычислитель B k модуля V k .

s ( t ) - анализируемый сигнал [9] в форме

L

s ( t ) = A Z ^rect [ t — ( l — 1)т э ]cos [ 2л ( d ki f + d^f ) t + n( b k! © D_r ) ] ,              (12)

i = 1

Здесь A - амплитуда; f н (в) - манипулируемые нижняя (верхняя) частоты; dkl е {0,1} и bkl е {0,1} - двоичные символы, принадлежащие циклически сдвинутой на к элементов исход- ной M -кодовой последовательности и соответствующие частотной и фазовой манипуляции l элемента сигнала; Dr - информационный символ, соответствующий дополнительной фазовой манипуляции.

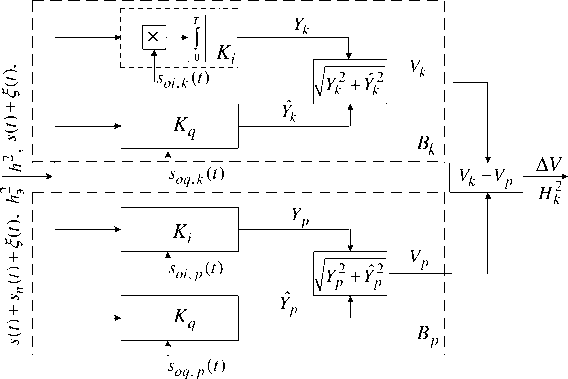
Рис. 3. Структурная схема распознавания ШПС-ЧММС сигналов

Fig. 3. Block diagram of ВВS-MSK signal recognition sn (t) - структурная помеха в форме сигнала, действующего от ближайшей опорной станции:

s n ⁽ t) = A n Z rect [ t ^{- ( l - 1)т} э ^]cos [ ²ⁿ ( d nl f н ⁺ d nl f 3 ) t ^{+ n( b}nl ® D n ) ^] ,               ⁽¹3)

здесь A n - амплитуда; f н _(в) - манипулируемые нижняя (верхняя) частоты; d_nl е {0,1} и b_nl е {0,1} - двоичные символы, принадлежащие циклически сдвинутой на n элементов исходной M -кодовой последовательности и соответствующие частотной и фазовой манипуляции l элемента сигнала; D_n - информационный символ, соответствующий дополнительной фазовой манипуляции.

^( t ) - флуктуационная помеха с равномерной (в полосе частот сигнала) спектральной плотностью мощности N_o .

s o k ( t ) - опорный сигнал, действующий в синхронном квадратурном корреляторе:

s o к ⁽ t ) = A o Z rect [ t ^{- ( l - 1)т} э ^]cos [ ²ⁿ ( d kl f н ⁺ d kl f в ) t ^{+ n b} kl ^] ,                ⁽¹⁴⁾

здесь A_o - амплитуда, можно принять равной 1;

• –    для вычисления составляющих Y_p и Y ˆ _p модуля V_p корреляции принятой реализации в форме s ( t ) + s n ( t ) + ^( t ) и опорного сигнала s o p ( t ), действующего в асинхронном квадратурном корреляторе, вычислитель B_p модуля V_p ;

• –    схему сравнения, по существу схему вычитания.

На рис. 4. представлены возможные диаграммы сигналов, действующих в схеме (рис. 3). Здесь sn (t) - сигнал действующей структурной помехи (13), в момент 10 начала анализа модулирующий код {dnl } соответствует циклически сдвинутой на n элементов исходной M -двоичной последовательности {dl} (для примера); so к (t) - опорный сигнал (14), в момент t0 начала анализа модулирующий код {dkl } соответствует циклически сдвинутой на k элемен- тов исходной M -двоичной последовательности {dl}; s(t) - анализируемый сигнал (12), в момент t0 начала анализа модулирующий код {dkl } соответствует циклически сдвинутой на k элементов исходной M -двоичной последовательности {dl}; so p (t) - опорный сигнал, в момент t0 начала анализа модулирующий код {dpl } соответствует циклически сдвинутой на p = nmin элементов исходной M -двоичной последовательности {dl}.

^s n ⁽ t )    • • П — 1

^s o , к ⁽ t ) • • к — 1

Т t o

^S o , p ⁽ t ) • • Р ^{— 1}

n

X

n + 1

ITT

• • • П — 1

к + 1 к + 2

k т =т a

• • • к — 1

^{s (} t ) • • к — 1

к	к + 1	к + 2	• • • к — 1

• • •

t p +1 p + 2

• • • Р — 1

p

• • •

t

• • •

t

• • •

t

Рис. 4. Диаграммы сигналов, действующих в схеме распознавания

Fig. 4. Diagrams of signals acting in the recognition scheme

Ошибочное решение при распознавании одного из двух ортогональных сигналов имеет место тогда, когда разность V_k — V_p имеет отрицательный знак, хотя выход нижнего вычислителя В_p не содержит распознаваемого сигнала. На выходах синхронного В_k и несинхронного В_p вычислителей формируются модули V_k и V_p с математическими ожиданиями и дисперсиями M ( V_k ) , M ( V_p ) и D ( V_k ) , D ( V_p ) соответственно. Для надёжной передачи информации при фазовой модуляции с вероятностью ошибки не хуже 1*10^–5 требуется отношение Сигнал/ Шум h = P т_э L / N o >  10 дБ ( P = A /2) — относительно сильный сигнал. При сильном сигнале можно аппроксимировать закон распределения модулей Рэлея – Райса нормальным законом. Тогда вероятность ошибки распознавания одного из двух сигналов можно определить как

P e = 1 — Ф ( Н к ),                                   (15)

где Ф ( Н_к ) — интеграл вероятности [10]; Н к — отношение Сигнал/ Шум на «выходе» схемы вычитания (рис. 3) определяется соотношением [11]:

н к = ( M ( V_t ) — M ( V p ) ) ²/ ( D ( V_t ) + D ( V p ) ) ,                        (16)

где M ( V k ), M ( V p ) и D ( V k ), D ( V p ) – математические ожидания и дисперсии модулей V_{p ( k )} на выходах синхронного В k и несинхронного В p вычислителей (рис. 3).

Также вероятность ошибки двоичного распознавания ортогональных сигналов, посредством некогерентной схемы (рис. 3), с энергией P τ _эL сигнала при действии помехи ξ( t ) со спектральной плотностью N_o можно определить через отношение h ² Сигнал/ Шум, используя известное выражение [7]

P e = e h /2 /2,                                      (17)

где h2 = PтэL / No, отношение Сигнал/Шум, при котором на входе схемы (рис. 3) действует сигнал, длительностью τэ L. Приравняв (15) и (17), по значению Hk2 , можно определить эквивалентное отношение hэ2 Сигнал/ Шум на входе схемы распознавания ортогональных сигналов с помощью формулы h2 = -2Ln{2[1 -Ф(Hk)]} .

Действие на входе схемы (рис. 3) дополнительно структурной помехи sn (t) приведёт, с учётом (15) и (17), к вероятности ошибки распознавания, которая будет определяться теперь уже эквивалентным отношением hэ2 Сигнал/ Шум, вычисляемым выражением (18). Здесь отношение Сигнал/ Шум Hk2 на «выходе» схемы вычитания (рис. 3) будет теперь определяться воздействием помехи sn (t) . Отсюда, теперь можно определить и эквивалентные энергетические потери a hk=h2 - нк,

обусловленные совместным действием сигнала с отношением Сигнал/ Шум h ² и структурной помехи s_n ( t ) , приводящей к эквивалентному отношению Сигнал/ Шум h _э² в сигнале схемы вычитания (рис. 3).

Модули V_k и V_p в (16), как случайные величины, распределены по закону Рэлея – Райса с параметрами математического ожидания и дисперсии [12]

M ( V , ) = a^ F , ( h , ²) = =kl

f 23 ^

1 + t । к 2 У

o

fh 2 ^

t

к У

+ h i I, 2¹

f h2)

к

- н 2

D V ) = 2a²

f A?) 1+1

к 2 У

- M ² V ),

где a - среднеквадратическое отклонение квадратурных составляющих модуля V , , отношение сигнал/шум на «выходах» квадратурных корреляторов:

h , ² = [ M ²( Y , ) + M ² (Y , )]/ a 2 = { M ² [ R_ki y , cos(ф) + n_y ] + M ² [ R_ki y_; sin(ф) + n y ]}/ ( N 0 T / 4) =

= R k_t ( AT / 2)² / ( N 0 T / 4) = 2 R PT / N_o = 2 R ^ ² E / N o = 2 h ² R ^ ² ,

здесь Rk , - коэффициент взаимной корреляции анализируемого и опорного сигналов; Ir (*) - модифицированная первого рода функция Бесселя r порядка [9].

Дисперсия флуктуационной помехи в выходных сигналах корреляторов (модуля V )

D ( Y ) = a _м ² = LN ₀Т э /4.

С учётом (16) и (20), для H_k ² (16) с учётом (20) можно записать в форме

₂ _( M V k ) - M V ) ) ² _      2 ^[ F k ⁽ h ²) ^{- F} p ^{( h} p ) ]

^k "  D ( V k ) + D ( V p )   " ₄ , 2 ,2_ ^ПГ _F2_№2_{) + F}2_r,2₎l .

^{1       4 + h} k ^{+ h} p 2 L F k ⁽ h k ) ^{+ F} p ^{( h} p ) ]

На «выходе» синхронного коррелятора (рис. 3, B_k ) будут присутствовать два отклика – на анализируемый сигнал s ( t ) и на структурную помеху s_n ( t ) , определяемые периодической автокорреляционной функцией (ПАКФ) сигнала s ( t ) и периодической взаимной корреляционной функцией (ПВКФ) сигналов s ( t ) и s_n ( t ) . Совместно будет действовать также и отклик на флуктуационную помеху.

Математические ожидания для синфазной и квадратурной составляющих [7] модулей V_{k ( p )}

синхронного и асинхронного квадратурных корреляторов (рис. 3, 4, B_k и B_p ) могу быть записаны в форме

M ( y_fc ) = PPTT TR_kk ^(т) COS(to o ^T + ф) + V P ^{2 2} TR nk ^(T n ) COS(to o ^T n + Ф n ) M ( l k ) = PF2TTR kk (T) sin(to o т + ф) + PnP /j T TR nk (т n ) sin(to o т n + ф n ) М ( У р ) = Pp2T TR kp (T)COS(_M o T + ф) + pi /j T TR np (t n )cos(to o T n + ф n )’ M (F p ) = pmTR kp (T)sin(_M o T + ф) + P /J T TR np (T n )sin(to o T n + ф n )

где i - мощность анализируемого сигнала; i n = A n / 2 - мощность структурной помехи, R_kk (т) - коэффициент нормированной ПАКФ анализируемого сигнала s ( t ) c модулирующим кодом { d_kl }, соответствующему циклически сдвинутой на k элементов исходной M -двоичной последовательности { d l } и опорного сигнала s o _k ( t ) c модулирующим кодом { d_kl }, соответствующему циклически сдвинутой на k элементов исходной M -двоичной последовательности { d l }; т - задержка начала действия k -го элемента опорного сигнала s o , _k ( t ) относительно начала действия k -го элемента анализируемого сигнала s ( t ) (рис. 4); R_nk (т _n ) - коэффициент нормированной ПАКФ структурной помехи s_n ( t ) с модулирующим кодом { d_nl }, соответствующему циклически сдвинутой на n элементов исходной M -двоичной последовательности { d_l } и опорного сигнала s_{o , k} ( t ) C модулирующим кодом { d_kl } , соответствующему циклически сдвинутой на k элементов исходной M -двоичной последовательности { d_l } ; T _n - задержка начала действия n -го элемента структурной помехи s_n ( t ) относительно начала действия p -го элемента опорного сигнала s_{o , p} ( t ) (рис. 4); R_kp (T) - коэффициент нормированной ПАКФ анализируемого сигнала s ( t ) и опорного сигнала s o _p ( t ) с модулирующим кодом { d_p l }, соответствующему циклически сдвинутой на p элементов исходной M -двоичной последовательности { d l }; R_{n p} (т _n ) - коэффициент нормированной ПАКФ структурной помехи s_n ( t ) и опорного сигнала s o _p ( t ); to _o - циклическая центральная частота; ф и ф _n - дополнительные набеги фаз [12], обусловленные параметрами трассы распространения поверхностной электромагнитной волны; cos( * ) и sin( * ) - корреляционные функции высокочастотных заполнений на центральной частоте.

Используя соотношения для тригонометрических функций [13], находим из (21) и (23) отношение Сигнал/ Шум в «выходе» синхронного квадратурного коррелятора Вк (рис. 3) в виде hk = { [ VPT2 TRkk (т) cos(tooт + ф) + VPn 22 TRnk (тn ) cos(tooTn + фn )]2 +

+ [ 4pTT TR kk T ) sin(to o т + ф) + ppT TR nk (т n ) sin(to o т n + ф n ))]²}/ ( N o T / 4) =

= 2 h ² [ R ² (т) + KR n²k (т n ) + 2 ^R nk (T n ) R kk (т) cos ( ф( t ) ) ] ,                  (25)

где h ² = ( PT ²/2)/( N_oT /4) = 2 E / N o - отношение Сигнал/ Шум для анализируемого сигнала в «выходе» синхронного квадратурного коррелятора В_к; K = i n / i - интенсивность помехи;

cos[v( t )] = cos[to _o (т - т _n ) + ф - ф _n ]                            (26)

- совместная корреляционная функция высокочастотного заполнения на центральной частоте to _o .

Отношение Сигнал/ Шум в выходном сигнале (модуль Vp) несинхронного квадратурного коррелятора Вр (рис. 3.) можно определить посредством (20) и (23) и с учётом тригонометрических функций [13] получим h2 = { [ Vp?2 TRkp (т) cos(tooт + ф) + 4Рп 22 TRnp (Tn ) cos(tooTn + фn )]2 +

+ [ 4PT2 TR kp (т) sin(to o т + Ф) + J- T TR np (t _n ) sin(® o т _n + ф _n )]²}/( NT /4) =

= 2 h ² [ R 2p (t) + KR ^ (t n ) + 2 4KR kp (t) R^ (t _n) cos ( V( t) ) ] .                  (27)

Согласно (25) и (27), отношения Сигнал/ Шум h_k ² и h_p ² определяются cos[ψ( t )] , где фазовый угол ψ( t ) (26) нестационарный случайный процесс [14] и учесть его значение в аппаратуре обработки принимаемых сигналов бортовой станцией практически невозможно. Область изменения ф( t ) составляет ± п, то верхней и нижней границам вероятности ошибки синхронизации при поиске будет соответствовать cos[^( t )] = ^1. Таким образом, при поиске отношения

Сигнал/ Шум hk2 и hp2 могут находиться в границах двух экстремальных значений, определяе- мых формулами h2 = 2h2 [Rkk ± VKRnk ]2 h2 = 2h2 [Rkp ± VKRp ]2

Оценка воздействия СП при поиске ШПС – ЧММС

В РНС «Спрут» с целью обеспечения кодового разделения каждый из сигналов ОС сформирован в соответствии с циклически сдвинутым модулирующим кодом относительно исходного M -кода. В соответствии с этим коэффициенты корреляций (28) могут принимать значения уровня главного и боковых выбросов модуля (рассчитанный по формулам [15]) нормированной периодической автокорреляционной функции (НПАКФ) для широкополосного сигнала с ЧММС, при модулирующей кодовой последовательности (длины L = 16383), формируемой в генераторе M -последовательности (14-разрядный регистр с соответствующими отводами обратной связи). Согласно [15], форма вычисленной НПАКФ носит равнобочную (вверх и вниз сходящую) трапецию. При этом для вверх и вниз сходящих значений корреляционной функции, определяемых приблизительно равными интервалами (2500 τ _э ) задержек. На интервале 2501 т э ^ 13883 т э значение максимального выброса НПАКФ составляет 1,8*10^-2, среднее значение выбросов НПАКФ составляет 4,2*10^–3. В силу поведения главного выброса (3) минимальное значение 6,1*10^-6 может быть на интервале 3 т э ^ 16382 т э временных задержек. Согласно (28), при cos[^( t )] = - 1 коэффициент R_nk (т) должен принимать минимально возможное значение.

C учётом сказанного, наиболее приемлемым будут значения коэффициента R_nk (τ) , определяемого вверх сходящимся участком вычисленной НПАКФ на интервале задержек 3 т_э ^ 2500 т _э .

Если опорные станции удалены друг от друга на расстояние r =350 км, то при этом задержка распространения поверхностного сигнала составит τ_р ≃ 1,167 мс (используя скорость и - 3*10⁸ м/c распространения сигнала, совершаем ошибку порядка 0,1 %) и при т _э = 2,5*10^-6 с будет соответствовать «циклической задержке» n o = r / (и т_э) на 466 - 467 модулирующих двоичных символов { d_nl } . На рис. 5 представлены фрагменты излучаемого сигнала с циклическим сдвигом n i - 1 удалённой опорной станцией ( ОС i , i = 1,3 - возможные номера удалённых опорных станций), и принимаемого бортовой станцией ( БС _i ) того же сигнала, с учётом задержки т _p при его распространении, и приёма бортовой станцией ( БС_к , к = 1,3 - возможные номера ближайших опорных станций) излучённого сигнала с циклическими сдвигами n_k - 1 ближайшей опорной станцией ( ОС_k ). Здесь коэффициент корреляции R_nk (τ) будет определяться как задержкой т _p , так и циклическими сдвигами ( n_k - 1 и n i - 1) модулирующего кода { d_nl } исходной M -кодовой последовательности:

ОС i

БC i

^Т э ^L

Т э

ni- n i + 1 ••• L — 1| L\ 1 I 2 ••• ni- — 1

^ti 1

^T p   ^по ^т э

n i ^+ 1 1 •

VT”

tБi

n i I n i + 1 •••

t2;

t

• • L — 1 L ' 1 '2 • • • ni- — 1

n i I n , + 1 •••

^T ik •

t

^{Б C}k n k n k + 1 ••• n_k + n_o — 1 n k + no... l| 1 ••• n_k

^{1 n}k n kk ^{+ 1} •••

^tk 1

Т э L tk2

t

Рис. 5. Фрагменты излучаемых ОС и принимаемых БС сигналов

Fig. 5. Diagrams of the emitted FS and received AS signals

R nk (т) = R nk (T ik ) = R nk [( n k — 1)т э + т p — ( n i — 1)т э ] = R nk [( n_k + n_o — n i )т э ].             (29)

Для указанных опорных станций возможны следующие сочетания номеров удалённой и ближайшей опорных станций относительно бортовой станции: 1 и 2, 1 и 3, 2 и 3, 2 и 1, 3 и 1, 3 и 2. Выбираем циклические сдвиги модулирующего кода {dnl } исходной M -кодовой последовательности для OC1 : n1 — 1 = 0, OC2 : n2 — 1 = 24 , OC3 : n3 — 1 = 49 . Отсюда при известном no = 466 и возможных сочетаниях номеров ОС через (28) будут получены следующие тактовые номера задержек τik :

ОС1 и ОС2 ^ 25 + 466 - 1 = 490;

ОС1 и ОС3 ^ 50 + 466 - 1 = 515;

ОС2 и ОС3 ^ 50 + 466 - 25 = 491;

ОС2 и ОС1 ^ 1 + 466 - 25 = 442;

ОС3 и ОС1 ^ 1 + 466 - 50 = 417;

ОС3 и ОС2 ^ 25 + 466 - 50 = 441.

На рис. 6 представлен фрагмент вверх сходящегося графика модуля НПАКФ для ЧММС сигналов при дополнительной ФМ на интервале [361τ_э,540τ_э ] тактовых задержек (с целью получения высокого разрешения). Как видно из рис. 6, значение максимального выброса составляет не более 4*10^–3 и при значениях тактов 417, 441, 442, 490, 491 и 515 значения выбросов так же составляют не более 4*10^–3. Отсюда возможные значения коэффициента R_kn (τ) на интервале [361τ_э,540τ_э ] тактовых задержек не смогут превысить величину 4,0*10^–3 при тактовой задержке распространения сигнала n o.

Теперь рассмотрим возможные значения коэффициентов корреляций в (28) на интервале [361τэ,540τэ ].

Коэффициент R_kk (τ) соответствует синхронному вычислителю В k (рис. 3), то его значение соизмеримо с единицей (|т| <  т э / 2) и можно принять равным 1.

Как выше было показано, значения коэффициента R_kn (τ) не смогут превысить величину 4,0*10^–3.

При работе схемы распознавания (рис. 3) для второго сигнала выбирается циклический сдвиг n min = 5 относительно первого сигнала, при котором коэффициент взаимной корреляции

R min ( n mi n т э ) равен минимальной величине R min = 1/ L =5,1*10 ⁵ (рис. 7) и тогда коэффициент R_kp (τ) = R _min можно принять.

• ••

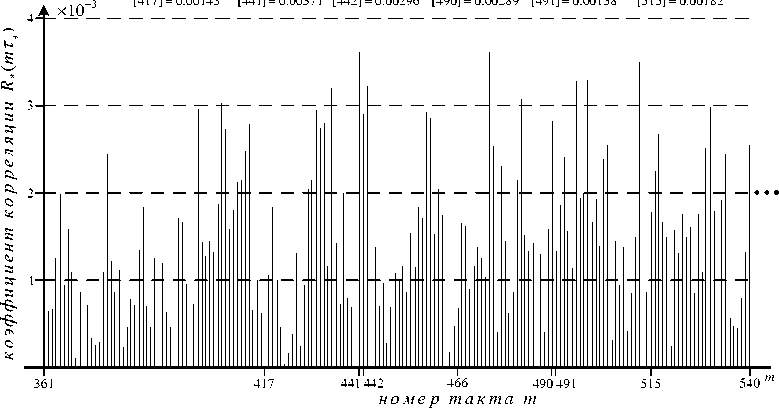
Рис. 6. Фрагмент графика модуля НПАКФ для ЧММС сигналов с дополнительной ФМ на интервале тактов [361,540]

Fig. 6. Fragment of the diadram normalized PACF module for MSK signals with additional FM on the clock interval [361,540]

Относительно второго сигнала (рис. 3–6) значения коэффициента R_np (τ) также будут находиться в интервале [361τ_э,540τ_э ] тактовых задержек и не превысят 4*10^–3.

Посредством (18), (17), (22) и (28) можно определить возможные эквивалентные потери энергии АhЭ анализируемого сигнала (ЭПЭАС) при заданном значении отношения Сигнал/ Шум h2 , обусловленные действием структурной помехи в форме сигнала sn (t) интенсивностью K , возможных значениях коэффициентов Rkn и Rnp и экстремальных значениях cos[^(t)] = ±1. На рис. 8 показана зависимость ЭПЭАС при h2 ^ 10 дБ и коэффициентах корреляций Rkn , максимальном 3,9*10–3 и (для примера) определяемых возможными сочетаниями номеров удалённой и ближайшей опорных станций относительно бортовой станции: 3 и 2 ^ 3,71*10-3, 1 и 2 ^ 2,89*10-3, 2 и 3 ^ 1,38*10-3. Из анализа рис. 8 следует, что поиск сигналов совместно со структурной помехой при её интенсивности K может проводиться в пределах верхней (cos(^(t)) < 0) и нижней (cos(^(t)) > 0) границ вероятности ошибки синхронизации. При поиске сигналов и cos(^(t)) > 0 отрицательное действие структурной помехи sn (t) исключается. Из поведения графиков (рис. 8) следует, что меньшему значению коэффициента Rkn(p)(τ) соответствуют и меньшие ЭПЭАС. При действии структурной помехи с интенсивностью не более 34 дБ допустимыми эквивалентные потери энергии анализируемого сигнала составят не более 3 дБ (при минимальном значении коэффициента корреляций Rkn =1,38*10–3 – не более 2 дБ) и эквивалентное отношение Сигнал/ Шум h2 составит не более h2 - Аh2 = 7 дБ. Таким образом, чтобы обеспечить надёжный поиск анализируемого сигнала при отношении Сигнал/ Шум h2 ~ 10 дБ (обеспечить вероятность ошибки синхронизации не хуже 1*10-3 при ошибке синхронизации |т| < тэ / 2 , рис. 2) необходимо обеспечить h2 ~ 15 -16 дБ, но с учётом потерь Сигнал/ Шум составляет h2 ~ 7 дБ, что для поиска потребует дополнительного некоге- рентного накопления до 15–16 дБ. Величине 7 дБ соответствует относительно сильный сигнал и тогда обобщённый закон Релея распределения модуля Vk можно аппроксимировать нормальным законом с математическим ожиданием M(Vi) и дисперсией D(Vi) (20), и тогда для обеспечения h2 ~ 15 -16 дБ необходимо произвести 8-кратное линейное накопление, и тогда «параллельный» поиск можно будет провести за 8Lтэ < 0,33 с (в РНС «Спрут» L = 16383, тэ = 2,5 мкс - длительность элемента сигнала).

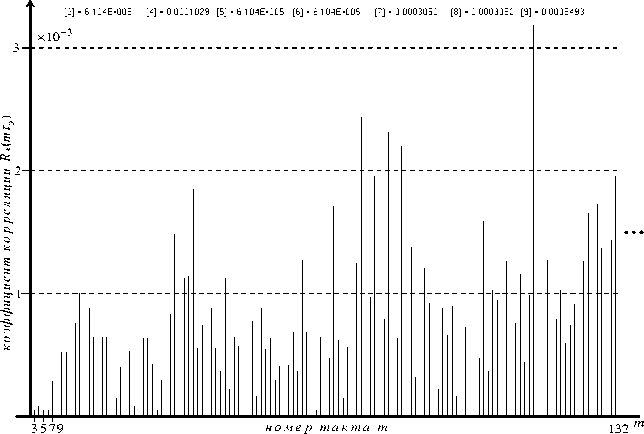
Рис. 7. Фрагмент графика модуля НПАКФ для ЧММС сигналов с дополнительной ФМ на интервале тактов [3,132]

Fig. 7. Fragment of the diadram normalized PACF module for MSK signals with additional FM on the clock interval [3,132]

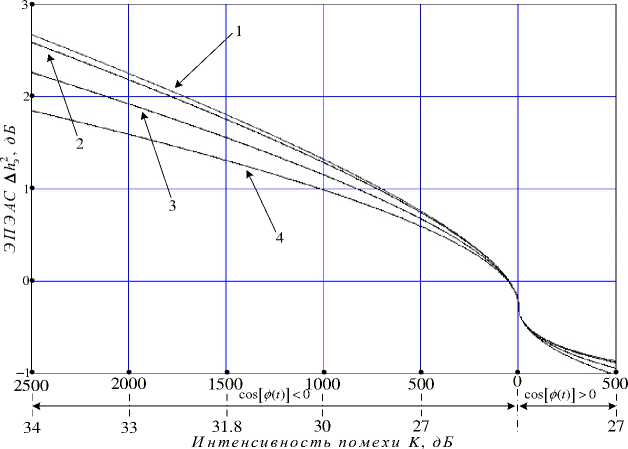
Рис. 8. Зависимость энергетических потерь анализируемого сигнала от интенсивности K :

1 - при R kn = 3,9*10^-3; 2 - при R kn = 3,71*10^-3; 3 - при R kn = 2,89*10^-3; 4 - при R kn = 1,38*10^-3

Fig. 8. The dependence of the energy losses of the analyzed signal on the intensity K :

1 - при R kn = 3,9*10^-3; 2 - при R kn = 3,71*10^-3; 3 - при R kn = 2,89*10^-3; 4 - при R kn = 1,38*10^-3

На рис. 9. представлена рабочая зона РНС (для РНС «Спрут» рабочая зона построена с учётом принятия максимального удаления от опорной станции до D _max = 600 км), образованная посредством 3-х совмещённых секторов, пересекающихся в точках П_ik , центрами которых являются местоположения ОС_i (для примера, на островах), а дуги d_i есть геометрическое место точек с максимальным удалением ( R ₁ = R ₂ = D _max ) от ОС_i . При движении бортовой станции от пункта П_a (ближайшее к OC ₂ место расположения БС ) к пункту П_b происходит удаление БС от всех OC и можно сказать, что происходит нарастание задержки распространения сигналов как от удалённой опорной станции OC ₁ , так и ближайшей опорной станции OC ₂ . В этом случае, при изменении трассы ∆ r ₁ распространения сигнала от OC ₁ и изменении трассы ∆ r ₂ распространения сигнала от OC ₂ относительно БС, коэффициент корреляции R_nk (τ _ik ) будет определяться

R_nk (τ _ik ) = R_nk [( n_k - 1)τ _э + τ _p + Δτ₁ - Δτ₂ - ( n_i - 1)τ _э ] = R_nk [( n_k + n_o - n_i )τ _э + Δτ] , (29)

Здесь Δτ₁ = Δ r ₁ / v - изменение задержки распространения сигнала от OC ₁ , Δτ₂ = Δ r ₂ / v - изменение задержки распространения сигнала от OC ₂ ( v - скорость распространения поверхностной электромагнитной волны). Разность изменения задержек Δτ при движении БС в правой полуплоскости относительно OC ₂ будет всегда отрицательной, так как Δ r ₂ ≥ Δ r ₁ , а при движении в левой полуплоскости уменьшается и τ _p , что говорит о невозможности превышения максимальной возможной величины τ _ik и коэффициент R_nk (τ _ik ) не превысит 3,9*10^–3. То же самое можно сказать и о поиске сигнала при остальных сочетаниях номеров удалённой и ближайшей опорных станций.

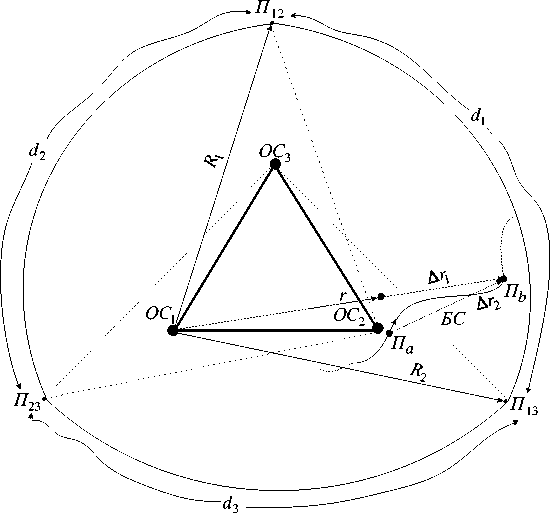
Рис. 9. Рабочая зона РНС с учётом расположения опорных и бортовой станций

Fig. 8. The working area of the RNS, taking into account the location of the support and on-board stations

Заключение

Предложенный в данной статье метод анализа воздействия структурных помех на поиск сигналов, у которых в качестве модулирующих кодов используют выбранные соответствующим образом, циклические сдвиги на n_i элементов одной и той же M -последовательности длины L = 16383. Показанный выбор циклических сдвигов позволяет использовать коэффициенты корреляций НПВКФ структурных помех на порядок меньше максимального (2,8*10^–2), что приводит к эквивалентным энергетическим потерям сигнала – поиска не более 3 дБ. Показанные условия поиска сигналов ОС в широкополосной РНС средневолнового диапазона позволяют эффективно применять кодовое разделение сигналов при использовании совмещённого радиоканала (для навигационных измерений и передачи данных) без ограничения рабочей зоны РНС, определяемой максимальным значением дальности D _max = 600 км.