Помехоустойчивость спутниковой связи при активных помехах и ограниченной полосе когерентности канала
Автор: Коротков Сергей Юрьевич, Пашинцев Владимир Петрович, Солчатов Максим Эриксович, Яремченко Сергей Владимирович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.11, 2013 года.
Бесплатный доступ
Разработана методика оценки вероятности ошибочного приема широкополосных сигналов в системах спутниковой связи в условиях возникновения частотно-селективных замираний из-за ограниченной полосы когерентности трансионосферного канала связи и одновременного воздействия узкополосной замирающей активной помехи на вход приемника.
Вероятность ошибки, спутниковая связь, широкополосный сигнал, трансионосферный канал, частотно-селективные замирания, активная помеха, коэффициент взаимного различия
Короткий адрес: https://sciup.org/140191659
IDR: 140191659 | УДК: 621.396.2
Текст научной статьи Помехоустойчивость спутниковой связи при активных помехах и ограниченной полосе когерентности канала
Постановка задачи
Известно [1-3], что в системах спутниковой связи (ССС) широкое применение находят сложные широкополосные сигналы (ШПС) с полосой спектра порядка 1 … 10 МГц. Они обеспечивают уменьшение вероятности ошибочного приема сигналов оптимальной схемой их обработки на фоне флуктуационных шумов (например некогерентной) при воздействии сосредоточенной по спектру активной помехи (АП). С другой стороны, известно [4-5], что при возмущениях ионосферы на высотах 150 … 400 км слоя F (например путем выброса химических веществ) образуются интенсивные неоднородности, вызывающие многолучевое распространение радиоволн и ограничение полосы когерентности спутникового (трансионосферного) канала связи (КС) до значений FK < 100кГц.
В этих условиях при передаче ШПС с типовыми параметрами:
-
- полоса спектра
-
- скорость
-
- длительность
-
- база
выполняется условие возникновения частотноселективных замираний (ЧСЗ) принимаемых сигналов Ш<1 при отсутствии их межсимвольной интерференции (МСИ) тл »1 • Появление ЧСЗ в принимаемых ШПС приведет к снижению достоверности приема (то есть к росту PQJ в ССС. Если ширину спектра передаваемых ШПС уменьшить с целью выполнения условия отсутствия ЧСЗ (FK/FO»1),то может существенно снизиться достоверность приема сигналов ССС к воздействию узкополосных АП. Отсюда следует, что в условиях одновременного ограничения полосы когерентности трансионосферного КС и действия АП имеется оптимальное значение полосы спектра ШПС, при которой обеспечивается наибольшая достоверность (минимальная ^ош) приема этих сигналов в ССС. Для определения этой частоты необходимо получить аналитическую зависимость ^ош от степени ЧСЗ (характеризуемой отношением FjFj принимаемых ШПС и степени влияния АП на обработку этих сигналов.
Целью статьи является разработка аналитической методики оценки помехоустойчивости широкополосных ССС в условиях ограниченной полосы когерентности трансионосферного канала и воздействия активных помех, позволяющей определить оптимальную полосу спектра ШПС по критерию обеспечения минимальной вероятности ошибки "
Решение задачи
Поставленную цель можно достичь на основе развития известной [5-6] методики оценки помехоустойчивости некогерентной (НК) схемы обработки ортогональных сигналов с ЧСЗ, реализованной на согласованных фильтрах (СФ) и квадратичных детекторах огибающей (КДО). Данная методика позволяет получить зависимость ^ош =^оЛч ^Ч'^/ЛЛ вероятности ошибки от отношения ho=E,jN6 энергии принимаемого сигнала Er к спектральной плотности мощности шума N^ и от коэффициента энергетических потерь rk^W^jF^ 1 при НК-обработке ШПС, подверженных ЧСЗ.
Эта зависимость получена при следующих предположениях:
-
- осуществляется передача двоичных символов (1 или 0) и соответствующих им ШПС с комплексными огибающими (КО) ^(Z) или S0(z);
-
- двоичный канал связи является симметричным, то есть FOUI=F(0/1) = F(1/0);
-
- передаваемые сигналы имеют одинаковые длительности ^Ts ) и энергии:
Ts Ts
E = Ex = Fo = J | S, (Z) 12 dt = J | So (012 dt; о 0
-
- КС является гауссовским, стационарным в широком смысле с некоррелированным рассеянием, регулярная составляющая отсутствует (то есть выполняется условие FJFO < 1 возникновения ЧСЗ);
-
- влияние МСИ на прием ШПС не учитывается, поскольку выполняется условие их отсутствия ТЛ »i •
Кроме этих традиционных допущений будем считать, что помимо гауссовских флуктуационных шумов на входе приемника действует узкополосная активная помеха. Поскольку полоса ее спектра намного меньше полосы ШПС: ^«Л» то будем считать, что при распространении помехи через возмущенную ионосферу выполняются условия отсутствия ЧСЗ: FjFn»\ и возникновения общих замираний (ОЗ) рэлеевского типа.
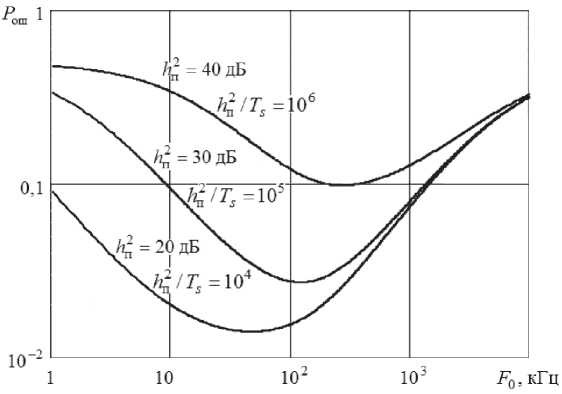
Тогда при передаче, например, сигнала Sx (Z) по многолучевому трансионосферному КС на вход НК-схемы обработки поступает аддитивная смесь комплексных огибающих принимаемого r сигнала Sr\(0 > подверженного ЧСЗ, гауссовского шума «(0 и активной помехи *^/ n(0 • xr^ = srXMVn = jS^t'-r) b(r) dr + n(t) + Srn(t). Здесь t' = t — t ; т = M(t) – среднее значение (математическое ожидание) времени запаздывания лучей в точку приема; t – отклонение времени запаздывания относительно T ; 6(r) -низкочастотная импульсная функция КС с рассеянием по времени. Входящие в (1) случайные процессы MO и 6(r) согласно сделанным предположениям являются гауссовскими и описываются нулевыми математическими ожиданиями (W[/i(Z)] = 0, Л/[6(т)] = 0) и корреляционными функциями вида: M [/7(Z) «(г/)] = N08(t—и); . * (2) M\b^ bdOA = сг(г)(г —и), где звездочка * означает знак комплексного сопряжения; ^(-Y) – дельта-функция; o-(z-) – функция рассеяния КС по времени. Выражение (1) для комплексной огибающей принимаемой аддитивной смеси X г W отличается от известного [5-6] наличием дополнительного слагаемого ^ГП (0 * Пусть комплексная огибающая передаваемой в момент времени t1 активной помехи с энергией Еп и описывается выражением sm = 4eu/m, (3) где Уп 01 ) - нормированная комплексная огибающая передаваемой помехи. Тогда комплексная огибающая принимаемой одновременно с сигналом sr и) активной помехи определяется как й?МЛ(1'НМ(О. (4) Здесь S п ( t ) – комплексная огибающая передаваемой помехи, приходящей на вход приемника одновременно с передаваемым сигналом 5*1 (f'), то есть в момент времени f = tx-i3=t-T; b^ – комплексный коэффициент передачи КС для замирающей помехи. Если его модуль (\bn\ = var) распределен по закону Рэлея с дисперсией \b„\2=2<7^ равной коэффициенту ослабления ^oc мощности помехи в КС, то средняя энергия замирающей помехи на входе ПРМ будет равна энергии принимаемой помехи в КС без замираний: |6п|2=2<т2=^ос; Era=2cy2En=K0A=Em. В соответствии с (1) и (4) комплексная огибающая аддитивной смеси принимаемого сигнала, шума и АП описывается выражением Xr (?) = j ^ (?' - r) 6( r) dr + n(O +МЭД. (6) При воздействии на вход НК-схемы обработки аддитивной смеси (6) на выходах согласованных фильтров первого и второго каналов обработки (СФ1 и СФ0) формируются взаимные корреляционные функции (ВКФ), значения которых в момент времени t' = T, определяются как L^^X^S^dt'; (7) О ^хдпзд'^т-. О Отклик первого согласованного фильтра Zj определяется автокорреляционной функцией (АКФ) передаваемого сигнала iS) (Z) и коэффициентом взаимной корреляции активной помехи ^n (^ ) с передаваемым сигналом ^i co * ^x-O^J^a'-^^CO^'; (9) ^П1 = /^(Г')^!^')^^- (10) Отклик второго согласованного фильтра ^0 пределяется ВКФ передаваемых сигналов ЭД И so(t) и коэффициентом взаимной корреляции активной помехи Sn (?) с передаваемым сигналом 50 (?): (11) 0 ZnO=JZn(?')So(?')^'. (12) На выходах КДО первого и второго канала схемы НК-обработки формируются дисперсии откликов £i и Lo согласованных фильтров: D(L1) = M(LlLl); D(L0) = M(L0L0). При равных энергиях передаваемых сигналов E^E0=E, сохранении условия их ортогональности |Ao(^ho и допущении об одинаковой коррелированности помехи ^n co с передаваемыми сигналами ^i co и •^o d) ’ то есть равенстве Rnl=Rn0=Rn, выражения (13) и (14) принимают следующий вид: D(Lt^ J|Zll(r)|2C7(r)^ + 2(72 |Zn |2+TV0^; О(ЕЭД2<у2ь\Ёп\2 +N0E. (16) В соответствии с (15)-(16) отношение «сиг-нал/шум» (далее С/Ш) на выходе НК-схемы обработки сигналов, подверженных влиянию ЧСЗ и АП, определяется как naa-DOa D(L0) J| ^H (Z") |'o-(r)c7 э . (17) ^E + 2^ |An|- Чтобы установить зависимость отношения С/Ш на выходе НК-схемы обработки W от отношения С/Ш на ее входе Ao =EJNO, воспользуемся нормированными представлениями для описания входящих в (17) АКФ передаваемого сигнала ^n(r), функции рассеяния КС cr(r) и коэффициента взаимной корреляции активной помехи с сигналом ^n ' Учтем, что комплексную огибающую передаваемого сигнала S, (?) можно представить в виде произведения 5Л1) = лГЁу1(0, где Д (0 – нормированная комплексная огибающая данного сигнала с условием нормировки J|7(o|2^=J|7(o|2^=i- Поэтому АКФ передаваемого сигнала 5,0) согласно (9) можно записать в виде r, » ^ll(-O = J^1(/-O^(/)^,= RnX=\sat'VSxkOdt' = =4ё^unutw =№ 4/nV (2i) где VnX=\Ut'WW' = Rtil4E7E - (22) о нормированный коэффициент взаимной корреляции активной помехи ^n (^) с сигналом *91 (0 • В соответствии с выражениями (18)-(22) отношение С/Ш на выходе НК-схемы обработки можно представить через входное отношение С/Ш Ao как 2cr‘ E- J кп(г)|"<тн(г)(/г W =---------------------------=----. (23) 7V0£ + 2a;|(/n|-£En l + A^Onl’ Здесь }4=2^Е^й=Е>й=Ег1Нй (24) – это отношение средней энергии e,=^; eK = e,. принимаемого сигнала в КС с рэлеевскими ОЗ (соответствующей энергии принимаемого сигнала в КС без замираний) к спектральной плотности NQ шума; = ^j /1 (0 - 0 /1 (0) /0 = ^^11 (-0, (18) 0 |0п(Орн(О^?-< 1 где ^i i (-o=/ 7; o' - о J; o') dr=r, । <-a/e (19) – нормированная АКФ передаваемого сигнала S’] (?) с максимальным значением ^H(r = O) = J|/(/)pZ' = l. Учтем, что фун-о кцию рассеяния КС по времени можно предста- вить в виде o-(t) = 2ct; где 2ct^ – мощность коэффициента передачи КС с рэлеевскими общими замираниями (ОЗ), а o"„(0 – нормированная функция рассеяния КС. В соответствии с (3) для комплексной огибающей активной помехи ЁЛ^ = 4Ёпул^ ее коэффициент взаимной корреляции (10) с передаваемым сигналом S^^EMO можно за- писать в виде – коэффициент энергетических потерь (то есть уменьшения отношения С/Ш на входе приемника A,)) при НК-обработке сигнала, подверженного ЧСЗ; /гп2 =2<тХМ = д;х =E,.JNo =PrJjN6 (26) - отношение средней энергии помехи на входе приемника Ero=2aX=E (соответствующей энергии принимаемой помехи Em = P.-J, с мощностью P( в КС без замираний) к спектральной мощности шума Ng . В соответствии с (23) выражение для оценки величины ^OLU при НК приеме сигналов, подверженных влиянию ЧСЗ и АП, принимает вид °'" 2+w г+лХ/о+АпХ |2)' (27) В частном случае отсутствия АП отношение «помеха/шум» (далее П/Ш) на входе приемника A" =° и выражение (27) сводится к известному [5-6] виду Рош=1/(2 + И/) = 1/(2 + /г27ч), (28) характерному для оценки ^ош при НК-приеме сигналов в КС с ЧСЗ. Выражение для коэффициента энергетических потерь Лч (25) при НК-обработке сигнала с ЧСЗ в [7] конкретизировано для случая передачи ШПС по трансионосферному КС с ЧСЗ в виде Согласно (29) при возникновении ЧСЗ в принимаемых ШПС UfJFq< 1) значение 7Ч< Ь а при их отсутствии (FJF0^cc) величина 7ч = 1 и выражение (28) сводится к известному [2-3] виду Рош=1/(2 + Л2), характерному для НК-приема сигналов в КС с рэлеевскими ОЗ. В частном случае отсутствия ЧСЗ ( 7ч = 1 ) при действии АП выражение (27) сводится к виду 1 _________________1_________________ 2 + W 2 + Лц/(1 +А21 ^ |2) (30) Сравним полученное выражение (30) с известной [3] формулой для оценки ^ОШ при НК-приеме сигналов с рэлеевскими замираниями (когда 7ч =1 ) при воздействии сосредоточенной по спектру помехи (с полосой ^<7^), подверженной рэлеевским ОЗ: ^..=0,5 (А„+2) [1 + /?^ g2n/(Ag+2)] ’- (31) где g,7n – коэффициент взаимного различия принимаемого сигнала и активной помехи. Последний зависит от отношений С/Ш Ад и П/Ш A 2 на входе ПРМ и базы сигнала BS=TSFOкак gr. ^ p Л^- = p- p (32) h T F h P T F где g^P^F. - нормированное значение коэффициента взаимного различия сигнала и помехи; p - некоторая постоянная для заданных параметров сигнала и помехи величина {\ В частном случае отсутствия АП коэффициент g^-n= 0 и выражение (31) сводится к виду ^)Ш=1/(2 + Л2), характерному для КС с рэлеевскими ОЗ. Заметим, что формулу (31) можно записать в более удобном виде: " 2 + й2/(1 + й^;2п/2) — 7 2 1 . 7 2 M X — (33) г + ^Ди-л^^./г) ' ' "FaFpFhFFpPFTy Данное выражение при больших значениях входного отношения С/Ш (Ao »1) сводится к известному виду [3] h^pY-va'h1 g1 ) h^lpVA-a'h1p[T.F0Y (34) где значение a' = \/2 соответствует случаю передачи ортогональных сигналов с неперекрыва-ющимися спектрами. При передаче сигналов с перекрывающимися спектрами (что характерно для КС с ШПС) значение a' = 1 и выражение (34) сводится к виду On,~A2/(l + /,2g2 _______________1_______________ Wo+^/w’ Заметим, что полученное выше выражение (30) при больших значениях входного отношения С/Ш (/72»1) сводится к виду, аналогичному (35): °ш 2 + ^ Л2/(1 + Л>п|2) A2,,/ где коэффициент ^n =l/(l + /22 |^n J") < 1 характеризует энергетические потери (то есть уменьшение отношения С/Ш на входе приемника Ag) при НК-обработке сигналов из-за воздействия АП. Сравнительный анализ выражений (36) и (35) показывает, что квадрат модуля нормированного коэффициента взаимной корреляции активной помехи и передаваемых сигналов I ^П | соответствует нормированному коэффициенту взаимного различия сигналов и помехи g,2nH (32), зависящему от базы сигнала: I ^„ |2 - gL - p!tsf0' Подстановка (38) в (37) позволяет получить зависимость энергетических потерь при НК-приеме ШПС из-за воздействия АП от отношения «помеха/шум» на входе приемника h^ к базе сигнала (Bs = TSFOY r?n=l/(l + hlp/TsF0) Согласно (39) по мере расширения полосы ^Q спектра ШПС энергетические потери при НК-приеме сигналов из-за воздействия АП снижаются (^П ^0- Ранее отмечалось, что для произвольной АП с сосредоточенным спектром в полосе Fu значение p лежит в пределах (<р<Т^<Т^. Поэтому значение нормированного коэффициента g™ = кп I будет находиться в пределах i/^^knl^^H^1. В частном случае воздействия идеализированной сосредоточенной помехи, под которой понимается гармоническое (синусоидальное) колебание с частотой, совпадающей с одной из гармонических составляющих сигнала, значения pи К I будут минимальными: p = 1; \^=g^=VTsF0. В этом случае коэффициент ^n (39) принимает наибольшее значение ^i/U+k Itsf^y которое можно использовать согласно (36) рош~^п„ для определения границы * В соответствии с (37) выражение (27) для оценки величины ^ОШ при НК-приеме сигналов, подверженных влиянию одновременно ЧСЗ и АП, целесообразно представить в виде p^x^h^n.Y (40) Для случая передачи ШПС входящий в (40) коэффициент энергетических потерь при НК-обработке сигнала из-за ЧСЗ зависит согласно (29) только от степени ЧСЗ Пч -'iAFJFp. а коэффициент энергетических потерь при НК-обработке сигнала из-за АП согласно (39) зависит от отношения П/Ш на входе ПРМ и базы сигнала Пп=/№л)- С учетом этих зависимостей искомое выражение для оценки величины ^ош при НК-приеме ШПС, подверженных влиянию одновременно ЧСЗ и АП, будет иметь следующий вид: 2 + Ао'7ч Пч Анализ полученной зависимости (41) Pom=ip(h^,FjF0,h;/TsF0)показывает, что по мере расширения полосы спектра F» передаваемых ШПС при заданных значениях отношения С/Ш на входе приемника h^ 5 полосы когерентности транстионосферного КС к<) и отношения i1n /Ps (соответствующего согласно (26) отношению мощности принимаемого сигнала к спектральной плотности шума PrJ^ =h;!T, ) влияние ЧСЗ на величину ^ОШ возрастает VFJFk ^co, rp -^0), а влияние АП – ослабля- ется иг^ТЛ^, Пч^ и наоборот. Так, при передаче ШПС с очень узкой полосой спектра (F0«FK,F0«h;jTa обеспечивается отсутствие ЧСЗ (Пч~^ при сильном влиянии АП (Пи « 1), а при выборе очень широкой полосы спектра ШПС (F0»FK,Fti»h;/Taобеспечи-вается отсутствие влияния АП (Пп » О при сильном влиянии ЧСЗ (Пч « !)• Рис. 1. Зависимость помехоустойчивости ССС от полосы спектра ШПС при ограниченной полосе когерентности канала ( F1( = 100 кГц) и различной мощности помех(PrjNo=h;/Ts=lOA;lO5; IO6) Результаты решения задачи В соответствии с выражением (41) на рис. 1 построены графики зависимости ^ш=^о) вероятности ошибочного приема ШПС от выбора полосы его спектра при заданных значениях отношения С/Ш на входе приемника hg ~ 20 дБ, полосы когерентности трансионосферного канала F = 100 кГц, величины p= 1 и различных отношений мощности принимаемого сигнала к спектральной плотности шума PrnlNn=hHT = ^\^, 106. Анализ графиков на рис. 1 указывает на существование оптимального значения полосы спектра Л, = ^op, передаваемых ШПС (Bs=TsF0»n, при которой обеспечивается минимальная величина ^ош при ^0 = const, зависящей от полосы когерентности FK трансионосферного КС и параметра h^T, влияния АП. Полученные аналитические зависимости (41) позволяют определить аналитическое выражение для оценки оптимальной полосы спектра F0=Fop, передаваемых ШПС при заданных значениях hg, FK, h^/Ts= const, обеспечивающее минимальное значение MINP_. Для этого необходимо найти производную по Fo от величины энергетического проигрыша Ю при НК-обработке сигналов из-за воздействия ЧСЗ и АП: q. n/L 4F" о P ^n T F ’ 1 s1 о 7 приравнять ее к нулю и решить уравнение C№) = o. С учетом выражения (42) для Учп это уравнение приводится к виду Решение этого уравнения относительно F» дает искомое выражение ( TtF1 p op* ( 4 No J Анализ (44) для определения оптимальной полосы спектра Fopl передаваемых ШПС показывает, что значение ^opt возрастает по мере расширения полосы когерентности трансионосферного канала связи FK и увеличения мощности помехи на входе приемникаUi2jTs=Prn/N0Y Выводы На основе развития известной методики оценки зависимости pom=yUF,FjFa вероятности ошибки при НК-обработке в ССС сигналов с заданной степенью частотно-селективных замираний На основе (41) получено аналитическое выражение (44) Fopt = v/(FKXk) для оценки оптимального значения полосы спектра F() — -^opt передаваемых ШПС, обеспечивающее минимум ^O[[l при заданных значениях полосы когерентности трансионосферного канала связи FK и отношения мощности помехи к спектральной плотности шума на входе приемника h;)Ts =P,.JNO.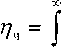
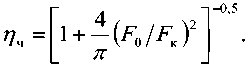
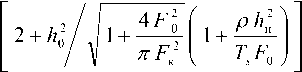
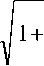
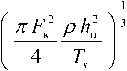
Список литературы Помехоустойчивость спутниковой связи при активных помехах и ограниченной полосе когерентности канала
- Ипатов В.П. Широкополосные системы и кодовое разделение каналов. Принципы и приложения. М.: Техносфера, 2007. -488 с.
- Варакин Л.Е. Системы связи с шумоподобными сигналами. М.: Радио и связь, 1985. -284 с.
- Сикарев А.А., Фалько А.И. Оптимальный прием дискретных сообщений. М.: Связь, 1978. -328 с.
- Богуш Р.Л., Гильяно Ф.У., Непп Д.Л. Влияние частотно-селективных эффектов распространения радиоволн на автоматическое слежение за сигналом в приемниках широкополосных систем связи//ТИИЭР. Т. 69, № 7, 1981. -С. 21-32.
- Маслов О.Н., Пашинцев В.П. Модели трансионосферных радиоканалов и помехоустойчивость систем космической связи. Приложение к ИКТ. Вып. 4, 2006. -357 с.
- Пашинцев В.П., Тишкин С.А., Солчатов М.Э. Влияние частотно-селективных замираний и межсимвольной интерференции на помехоустойчивость высокоскоростных систем космической связи//Известия ВУЗов. Радиоэлектроника. №9, 2001. -С. 49-60.
- Пашинцев В.П. Влияние частотно-селективных замираний на измерение времени запаздывания сигналов систем космической связи//Радиотехника и электроника. Т. 43, № 4, 1998. -С. 410-414.


