Понижение порядка сложных моделей с помощью инструментов Robust Control Toolbox

В городе Березники (Пермский край) на протяжении уже нескольких лет проводится мониторинг зданий и сооружений. Это связано с проседанием почвы, так как практически под всем городом находятся не используемые выработки шахт калийного производства.

Для качественного анализа и прогнозирования необходимы достаточно точные модели. Порядок этих моделей может быть очень большим, что усложняет их дальнейшую обработку и увеличивает затрачиваемые ресурсы времени.

Цель данной статьи – рассмотреть набор инструментов Robust Control Toolbox для понижения порядка сложных моделей на конкретном примере.

Так как у нас нет доступа к данным мониторинга, то в качестве примера возьмем модель движения твердого тела здания больницы университета в городе Лос-Анджелесе. Модель взята из рабочей заметки SLICOT 2002-2 «Сборник эталонных примеров для редукции моделей линейных динамических систем, не зависящих от времени», авторы: Y. Chahlaoui и P.V. Dooren .

В здании восемь этажей, на каждом по три степени свободы – два смещения и одно вращение. В данных имеются отношения вход – выход для любого из этих смещений. В результате получается модель в пространстве состояний с 48 состояниями, где каждое из них представляет собой смещение или скорость его изменения.

В toolbox Robust имеется набор инструментов для работы с моделями высоких порядков. Такие модели, как правило, получаются при точной идентификации технологических объектов, когда мы используем функции взвешивания частоты для формирования отклика разомкнутого контура. Часто мы хотим упростить такие модели для целей моделирования или проектирования систем управления. Как правило, достаточно иметь точную модель вблизи частоты среза. Для моделирования достаточно зафиксировать существенную динамику в диапазоне частот сигналов возбуждения. Это означает, что часто можно найти приближения более низкого порядка для моделей высокого порядка. Модуль Robust Control Toolbox предлагает множество алгоритмов сокращения моделей, которые наилучшим образом соответствуют нашим требованиям и характеристикам модели [1].

Процесс редукции модели

Задача редукции модели обычно включает следующие шаги [2, 3].

• 1.    Анализ важных характеристик модели по ее откликам во временной или частотной области с помощью команд step или bode [4, 5].

• 2.    Определение порядка сокращения, вычислив сингулярные значения Ганкеля ( hankelsv ) исходной модели и построив по ним соответствующие гистограммы, чтобы определить, какие режимы (состояния) можно отбросить, не жертвуя ключевыми характеристиками. Обычно отбрасывают значения, близкие к нулю [6].

• 3.    Выбор алгоритма редукции. В наборе инструментов toolbox Robust доступны следующие функции сокращения: balancmr , bstmr , schurmr , hankelmr и ncfmr . Мы можем легко получить доступ к этим алгоритмам через интерфейс верхнего уровня с помощью команды reduce . В методах используются разные оценки «близости» между исходной и редуцированной моделью. Выбор зависит от используемых параметров команды [3].

• 4.    Проверка. На данном этапе мы проверяем наши результаты, сравнивая динамику сокращенной модели с исходной моделью. Нам может потребоваться скорректировать параметры редукции (выбор порядка модели, алгоритма, границ ошибок и т. д.), если результаты неудовлетворительны.

В рассмотренном выше здании восемь этажей, на каждом по три степени свободы – два смещения и одно вращение. В данных имеются отношения вход – выход для любого из этих смещений. В результате получается модель в пространстве состояний с 48 состояниями, где каждое состояние представляет собой смещение или скорость его изменения [7–9]. Применим методы редукции к данной модели.

Откроем модель и построим график логарифмической амплитудно-частотной и фазочастотной характеристики (АФЧХ). Для этого выполним команды:

В результате получим график, приведенный на рис. 1.

Как видно из частотной характеристики модели, основная динамика системы лежит в диапазоне частот от 3 до 50 рад/с. Величина падает как в очень низком, так и в высокочастотном диапазоне. Наша цель – найти модель низкого порядка, которая сохраняет информационное содержание в этом частотном диапазоне до приемлемого уровня точности.

Чтобы понять, какие состояния модели можно безопасно отбросить, вычислим сингулярные значения Ганкеля для нашей модели [10–12]. Для этого выполним команду hsv_add = hankelsv(G);

• и построим гистограмму сингулярных значений:

bar(hsv_add)

title('Hankel Singular Values of the Model (G)');

xlabel('Number of States')

ylabel('Singular Values (\sigma_i)')

line([10.5 10.5],[0 1.5e-3],'Color','r','linestyle','--','linewidth',1)

text(6,1.6e-3,'10 dominant states.')

В результате получим гистограмму, приведенную на рис. 2.

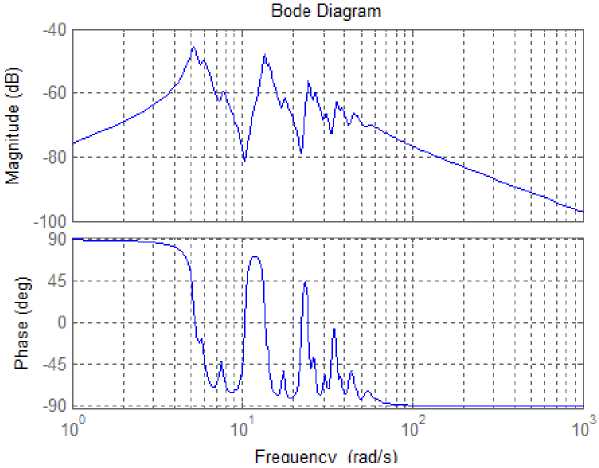
Рис. 1. График АФЧХ исходной системы Fig. 1. APАС plot of the original system

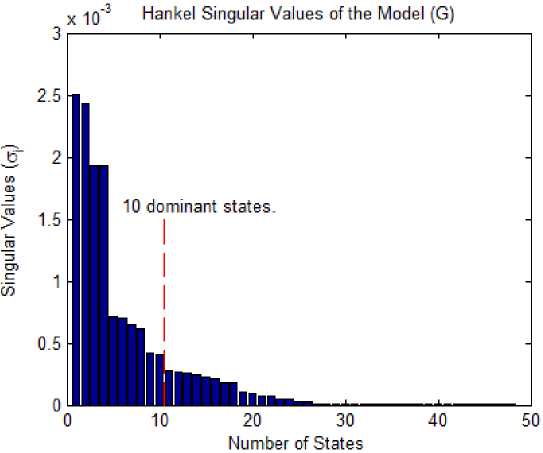
Рис. 2. Гистограмма сингулярных значений Ганкеля для исходной модели

Fig. 2. Hankel singular values for the original model

Из графика сингулярных значений Ганкеля видно, что в этой системе есть четыре доминирующих режима. Однако вклад остальных мод все же значителен. Мы проведем линию через 10 состояний и отбросим оставшиеся, чтобы найти сокращенную модель 10-го порядка ( Gr ), которая наилучшим образом приближает исходную систему ( G ).

Функция reduce является шлюзом ко всем процедурам редукции моделей, доступным в наборе инструментов [13, 14]. Мы будем использовать параметр усечения баланса квадратного корня по умолчанию ' balancmr ' для функции reduce как первый шаг. В этом методе для уменьшения порядка используется «аддитивная» граница ошибки, что означает, что он пытается поддерживать одинаково малую абсолютную ошибку аппроксимации по частотам.

Данный метод используется в функции по умолчанию.

Вычислим сокращенную модель 10-го порядка. Для этого выполним команду

[Gr_add,info_add] = reduce(G,10);

Для сравнения исходной ( G ) и редуцированной модели ( Gr_add ) построим графики их АФЧХ. Для этого выполним команды:

bode(G,'b',Gr_add,'r'), grid on title('Comparing Original (G) to the Reduced model (Gr\_add)')

legend('G - 48-state original ','Gr_add - 10-state reduced','location','northeast')

В результате получим графики, приведенные на рис. 3.

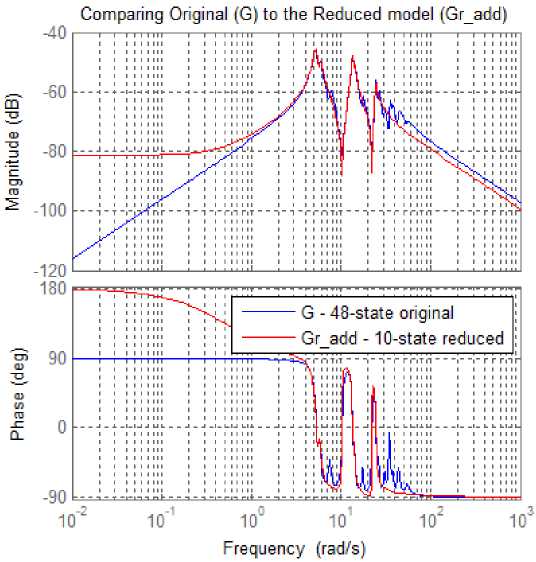
Рис. 3. АФЧХ исходной и редуцируемой модели Fig. 3. APFC original and reduced model

Как видно из графиков на рис. 3, упрощенная модель довольно хорошо улавливает резонансы ниже 30 рад/с, но согласование в области низких частот (< 2 рад/с) плохое. Кроме того, упрощенная модель не полностью отражает динамику в диапазоне частот 30–50 рад/с. Возможное объяснение больших ошибок на низких частотах – относительно низкий коэффициент усиления модели на этих частотах. Следовательно, даже большие ошибки на этих частотах мало влияют на общую ошибку [15, 16].

Чтобы обойти эту проблему, мы можем попробовать метод мультипликативной ошибки, такой как bstmr . Этот алгоритм делает упор на относительные ошибки, а не на абсолютные [17, 18]. Поскольку относительные сравнения не работают, когда коэффициенты усиления близки к нулю, нам нужно добавить порог минимального усиления, например, добавив сквозное усиление.

Под сквозным усилением понимается непосредственная связь входа с выходом. Такая связь существует, если значение матрицы d пространства состояний не равно нулю. Предполагая, что нас не беспокоят ошибки при усилении ниже –100 дБ, мы можем установить коэффициент усиления сквозной связи, равным 1e-5.

Для этого выполним команду

GG = G; GG.d = 1e-5;

Снова вычислим сингулярные значения Ганкеля и построим гистограмму:

Hsv_mult = hankelsv(GG,’mult’);

bar(hsv_mult)

title(‘Multiplicative-Error Singular Values of the Model (G)’);

xlabel(‘Number of States’)

ylabel(‘Singular Values (\sigma_i)’)

В результате получим гистограмму, приведенную на рис. 4.

Multiplicative-Error Singular Values of the Model (GG)

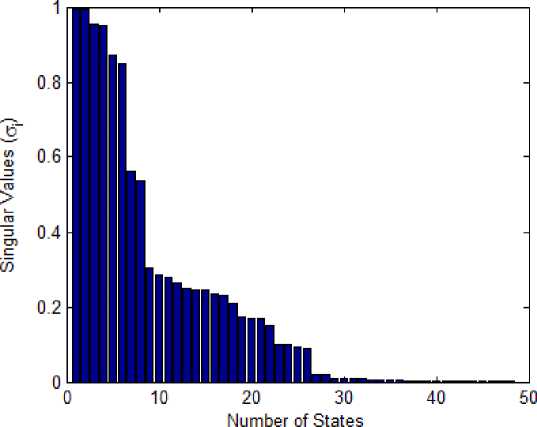
Рис. 4. Гистограмма сингулярных значений Ганкеля для редуцированной модели

Fig. 4. Histogram of Hankel singular values for the reduced model

Из диаграммы видно, что нам необходима модель 26-го порядка, но для сравнения с предыдущим результатом давайте придерживаться редукции на 10-й порядок. Используем опцию алгоритма bstmr для сокращения модели:

[Gr_mult,info_mult] = reduce(GG,10,'algorithm','bst');

Построим графики АФЧХ для исходной ( G ) и редуцированной ( Gr_add и Gr_mult ) модели:

bode(G,Gr_add,Gr_mult,{1e-2,1e4}), grid on title('Comparing Original (G) to the Reduced models (Gr\_add and Gr\_mult)')

legend('G - 48-state original ','Gr\_add (balancmr)','Gr\_mult (bstmr)','location','northeast')

В результате получим графики, приведенные на рис. 5.

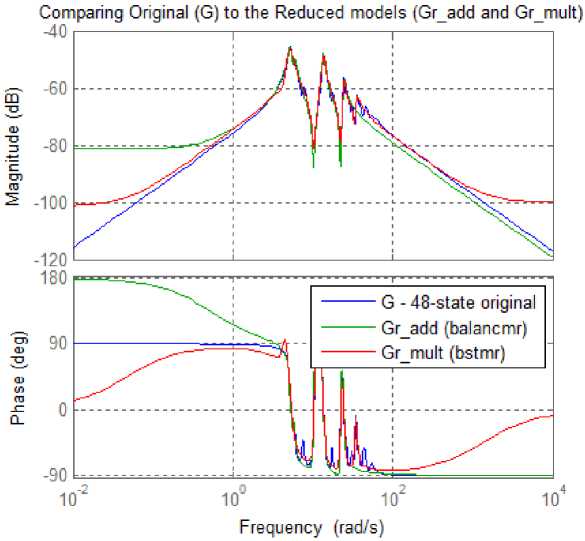
Рис. 5. Графики АФЧХ для моделей G, Gr_add, Gr_mult

Fig. 5. APFC plots for models G, Gr_add, Gr_mult

Соответствие между исходной и сокращенной моделями намного лучше при использовании метода мультипликативной ошибки даже на низких частотах. Чтобы подтвердить это, построим временные переходные процессы. Для этого выполним команды:

step(G,Gr_add,Gr_mult,15) %step response until 15 seconds legend(‘G: 48-state original‘,’Gr\_add: 10-state (balancmr)’,’Gr\_mult: 10-state (bstmr)’)

В результате получим графики, приведенные на рис. 6.

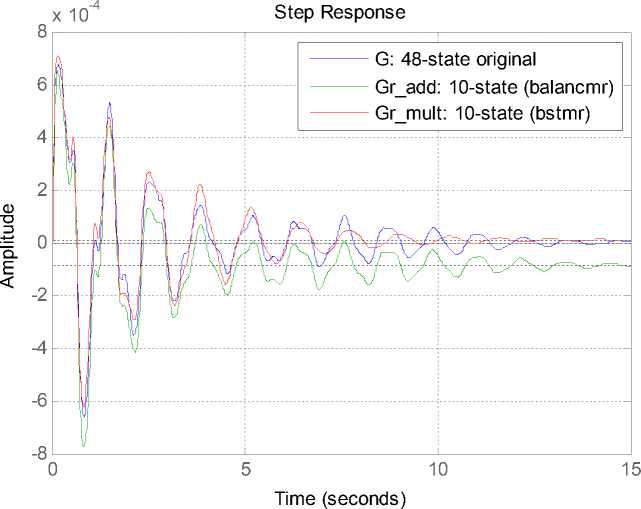
Рис. 6. Переходные процессы для моделей G, Gr_add, Gr_mult Fig. 6. Transients for models G, Gr_add, Gr_mult

Проверка результатов и корректировка модели

Все алгоритмы обеспечивают границы ошибки аппроксимации. Для методов аддитивной ошибки, таких как balancmr , ошибка аппроксимации измеряется пиковым (максимальным) коэффициентом усиления модели ошибки | G-Greduced на всех частотах. Максимальное значение можно получить, если вычислить бесконечную (Чебышевскую) норму вектора с помощью функции norm(A,inf). Теоретическая граница хранится в поле Error Bound структуры INFO, возвращаемой функцией reduce .

Для анализа выполним команды:

E1 = norm(G-Gr_add,inf)

E2 = info_add.ErrorBound

[E3,f] = norm(GG\(GG-Gr_mult),inf)

E4 = info_mult.ErrorBound

В результате получим:

E 1 = 6.004322380100927e–04 – абсолютная ошибка модели Gr_add ;

E 2 = 0.004718864240517 – теоретическое значение границы модели Gr_add ;

E 3 = 0.594921503759114 – максимальная относительная ошибка модели Gr_mult и соответствующая ей частота f = 17.2;

E 4 = 4.732954442311137e+02 – теоретическое значение границы модели Gr_multi .

Построим график относительных ошибок модели Gr_mult в частотной области. Для этого выполним команды:

figure;bodemag(GG\(GG-Gr_mult),{1e-2,1e3}); grid on text(0.1,-50,'Peak Gain: -4.6 dB (59%) at 17.2 rad/s')

title('Relative error between original model (G) and reduced model (Gr\_mult)')

В результате получим график, приведенный на рис. 7.

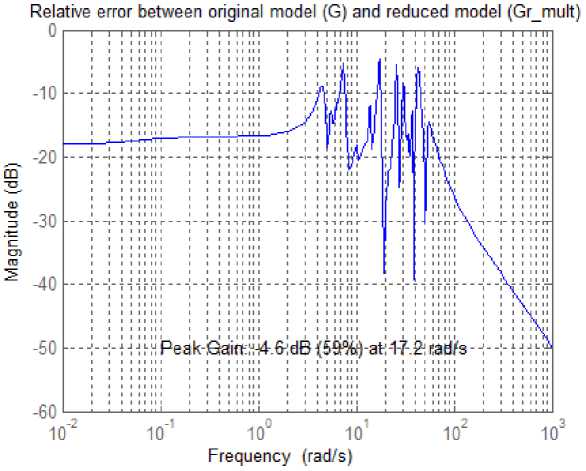
Рис. 7. График относительной ошибки модели Gr_mult Fig. 7. Graph of the relative error of the Gr_mult model

Из приведенного выше графика и сделанных расчетов можно увидеть, что максимальная относительная ошибка достигает 59 % при частоте 17,2 рад/с. В нашем случае это больше допустимого.

Функция reduce позволяет выбрать наименьший порядок, совместимый с желаемым уровнем точности. Чтобы повысить точность модели Gr_mult , нам придется увеличить порядок.

Зададимся максимальной ошибкой, равной 5 %, и выполним редуцирование с заданной точностью.

[Gred,info] = reduce(GG,'ErrorType','mult','MaxError',0.05);

Определим порядок полученного объекта:

P=size(Gred.a)

В результате получим P = 34. Следовательно, минимальный порядок модели, обеспечивающий 5%-ную ошибку, составляет 34.

Вычислим относительную ошибку и теоретическую границу модели Gred :

E5 = norm(GG\(GG-Gred),inf)

E6 = info.ErrorBound

В результате получим

E 5 = 0.0068 – максимальная относительная ошибка модели Gred .

E 6 = 0.0422 – теоретическое значение границы модели Gred .

Повышение точности достигнуто за счет увеличения порядка модели (с 10 до 34). Обратите внимание, что фактическая максимальная ошибка составляет 0,6 %, что намного меньше целевого показателя в 5 %. Это несоответствие является результатом функции bstmr , которая использует границу ошибки, а не фактическую ошибку, чтобы выбрать необходимый порядок.

И в заключение построим АФЧХ и переходные процессы исходной и редуцированной модели:

figure; bode(G,Gred,{1e-2,1e4}), grid on legend('G - 48-state original','Gred - 34-state reduced')

figure; step(G,'b',Gred,'r--',15),grid %step response until 15 seconds legend('G: 48-state original ','Gred: 34-state (bstmr)')

text(4,-5e-4,'Maximum relative error <0.05').

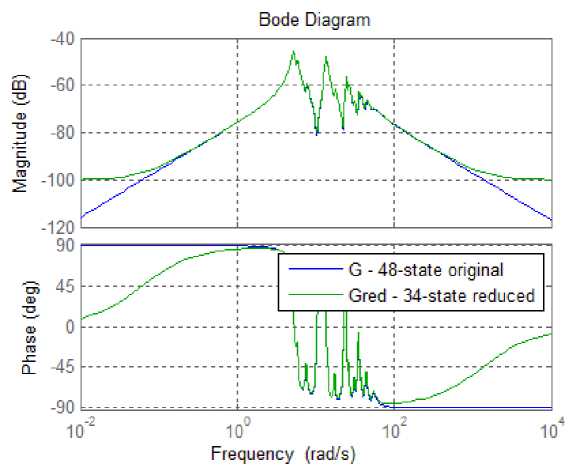
Рис. 8. АФЧХ исходной и редуцированной модели Fig. 8. APFC of the original and reduced model

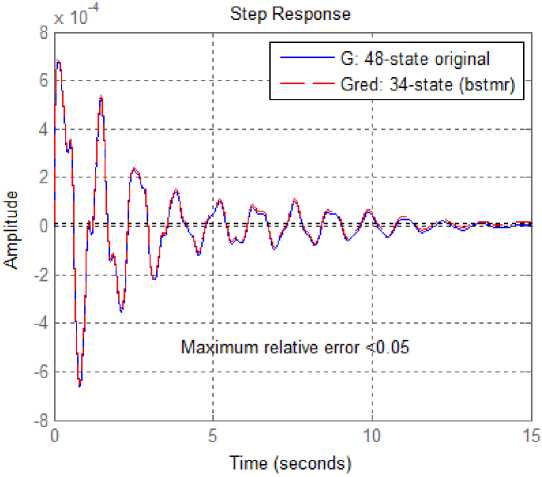
Рис. 9. Переходные процессы исходной и редуцированной модели Fig. 9. Transient processes of the original and reduced model

Анализируя рис. 8 и 9, мы видим, что графики в частотной области, где проявляется основная динамика объекта, практически совпадают. Ошибка аппроксимации составляет менее 5 %. В результате для адекватного описания системы мы смогли понизить ее размер на 14 порядков, что положительным образом должно сказаться на дальнейших расчетах и работе с данной моделью.