Поперечная интенсивность в остром фокусе цилиндрического векторного пучка второго порядка

Сканирующая ближнепольная оптическая микроскопия (СБОМ) занимает важное место в исследованиях в области плазмоники, нанофотоники и т.д. [1 – 3]. Благодаря СБОМ у исследователей есть возможность детектировать световые поля вблизи областей раздела двух сред в той зоне, где, помимо распространяющихся световых волн, фиксируемых средствами классической оптической микроскопии, присутствуют и затухающие волны, в регистрации которых обычный микроскоп бессилен.

Различают два типа кантилеверов для регистрации излучения в СБОМ: безапертурные (s-SNOM) и апертурные (a-SNOM). Несмотря на то, что в последнее время отмечается устойчивый рост использования без-апертурных СБОМ, интерес к апертурным СБОМ сохраняется, в том числе в силу большей сложности измерений с помощью безапертурных СБОМ методик.

Существует два типа апертурных СБОМ: на основе металлизированного заостренного волокна и полые пирамидальные кантилеверы. Отличительной особенностью апертурных СБОМ, как это ясно из названия, является наличие на конце зонда небольшого отверстия – апертуры, с помощью которой и осуществляется детектирование проходящего излучения. Диаметр отверстия колеблется от десятка до сотни нанометров. Само отверстие обычно имеет круглую форму. Однако для решения специфичных задач может использоваться и другая форма отверстия апертурного СБОМ кантилевера. В работе [4] исследовалась поляризационная чувствительность апертурных СБОМ кантилеверов с прямоугольным отверстием. Было показано, что пропускаемость излучения увеличивается, если поляризация падающего на кантилевер света направлена вдоль большей стороны прямоугольника.

В работе [5] апертурный СБОМ на основе волокна использовался для изучения интерференционной картины поверхностных плазмон-поляритонов, создаваемых светом разной поляризации. Интересный тип зондов был предложен в работе [6], где в отверстии пирамидального кантилевера была закреплена микросфера. Отдельного упоминания заслуживают апертурные кантилеверы с отверстием в форме «галстука-бабочки» (bowtie). Такие отверстия можно изготовить как на металлизированных волноводах [7, 8], так и в пирамидальных кантилеверах [9]. Такая форма отверстия работает как наноантенна, позволяя локально усиливать световое поле, например, для литографических целей. Поляризационные свойства пирамидальных кантилеверов исследовались в работах [10, 11], было показано, что в области ближнего поля такие кантилеверы более чувствительны к поляриза- ции проходящего через них излучения, чем вдали от раздела двух сред. Кантилевер с квадратным отверстием использовался в работе [12] для детектирования люминесцирующих наночастиц. В работе [13] исследовалась острая фокусировка лазерного излучения зонной пластинкой Френеля и было показано, что форма фокусного пятна, зарегистрированная стандартным пирамидальным СБОМ кантилевером ближе к форме поперечной составляющей интенсивности, а не суммарной интенсивности и не продольной компоненты вектора Пойнтинга.

Ранее нами численно исследовалась острая фокусировка цилиндрических векторных пучков второго порядка [14] и оптических вихрей с топологическим зарядом два [15] фазовыми зонными пластинками и было показано, что в центре фокусных пятен наблюдаются области, в которых направление вектора Пойнтинга противоположно направлению распространения пучка. Экспериментального исследования с помощью СБОМ острой фокусировки таких пучков ранее осуществлено не было.

Отметим, что зонные пластинки Френеля и металинзы на их основе получили широкое применение в области фокусировки излучения [16–21]. Отдельный интерес представляют спиральные зонные пластинки, которые позволяют одновременно формировать и фокусировать вихревой пучок [22–26]. В последнее время у научного сообщества возрос интерес к исследованию фокусировки более сложных векторных полей. Так, в [18] рассматривается металинза для эффективного управления амплитудой, фазой и поляризацией, которая была изготовлена на тонкой пленке аморфного кремния. При длине волны падающего излучения, равной 635 нм, наностержни из аморфного кремния сильно ограничивают магнитные дипольные резонансы с разностью фаз π и, таким образом, достигают высокого пропускания для кроссполяризации и нулевого коэффициента пропускания ко-поляризации. Изготовленная металинза показывает в 1,5 раза более высокую эффективность фокусировки, а также в 2,3 раза более высокую контрастность изображения, чем обычная ЗП на основе тонкой пленки хрома (100 нм). В работе [27] теоретически и численно исследовались характеристики радиально и азимутально поляризованных пучков после прохождения через плазмонные субволновые структуры в виде кольцевых щелей. В [28] c помощью FDTD-метода исследуется фокусировка цилиндрических векторных пучков спиральной металинзой с топологическим зарядом m = 1, числовой апертурой 1 и фокусным расстоянием, равным длине падающей волны. Показано, что данная линза создает вблизи поверхности фокальное пятно в форме круга с диаметром меньше дифракционного предела для падающих TE-волн или кольца для TM-волн, в картине интенсивности образующегося фокального пятна присутствуют локальные (симметричные и асимметричные)

области обратного потока энергии, которые могут располагаться как в центре, так и на периферии.

В данной работе рассмотрена фокусировка цилиндрического векторного пучка второго порядка амплитудной зонной пластинкой Френеля с фокусным расстоянием 532 нм и диаметром 15 мкм. Зонная пластинка изготавливалась средствами электронной литографии, химического травления и лифт-офф процесса в алюминиевой пленке толщиной 50 нм. Численно методом FDTD и с помощью формул Ричардса – Вольфа было показано, что такая зонная пластинка формирует в фокусном пятне на оси область, в которой направление вектора Пойнтинга противоположно направлению распространения пучка (область обратного потока энергии). И распределение продольной компоненты вектора Пойнтинга, и интенсивности имеют вид колец, но у продольной компоненты вектора Пойнтинга кольцо симметричное, а у интенсивности – асимметричное, обусловленное неравномерным вкладом различных составляющих. В частности, поперечная составляющая интенсивности ненулевая на оптической оси и имеет вид трех пиков, расположенных вдоль оси x . Затем область обратного потока исследовалась с помощью сканирующего ближнепольного оптического микроскопа Интегра Спектра (НТ-МДТ) на основе полого пирамидального апертурного кантилевера. Экспериментально фиксировалось пиковое распределение интенсивности в фокусе (с субволновыми размерами FWHMx=0,39λ и FWHMy=0,71λ). Данный факт является доказательством чувствительности кантилевера к поперечной составляющей интенсивности светового поля в области обратного потока энергии.

Дизайн и изготовление зонной пластинки

Зонные пластинки рассчитывались для освещения их длиной волны λ =532 нм и фокусировки на расстояние f = 0,532 мкм. Радиусы колец зонной пластинки рассчитывались по формуле r m =( m λ f – m ² λ²/4)^{1 ∕ 2}. Диаметр изготовляемых пластинок был равен 15 мкм. Числовая апертура линзы при таких параметрах равна NA=0,99749.

Для изготовления субволновых дифракционных оптических элементов использовалась технология, включающая литографию, химическое травление и лифт-офф процесс. В качестве подложки будущего элемента использовался кварцевый субстрат. Шероховатость поверхности составляла меньше 10 нм. Металлическая пленка напылялась на кварцевую подложку с использованием напыляющей магнетронной системы CarolineD12A (ESTO-Vacuum, Inc.). Металлический слой формировался в процессе осаждения алюминия. Все пленки осаждались при давлении в вакууме 10 –3 Па и мощности 300–700 Вт. Толщина алюминиевой пленки контролировалась временем напыления и составила 50 нм. Далее в центрифуге наносился резист для электронно-лучевой литогра- фии. Толщина нанесенного резиста была равна 400 нм (контролировалась на профилометре P-16 (KLA-Tencor, Inc.)). Экспозиция резиста выполнялась SEM-микроскопом с разрешением 10 нм. Затем химически осуществлялось удаление оставшейся маски из резиста. Получившаяся структура очищалась и запекалась для повышения адгезивных свойств. С помощью установки магнетронного напыления CarolineD12A (ESTO-Vacuum, Inc.) наносилась тонкая пленка хрома. Напыление происходило при следующих параметрах: 10 –3 Па и 700 Вт. Толщина пленки составляла 45 нм. Далее применялся лифт-офф процесс: с помощью ацетона удалялся резист вместе с пленкой хрома на нем. Это позволяло получить негативную маску в хроме по отношению к маске на резисте. Через пленку хрома металлический слой удалялся с помощью NaOH. На последнем этапе маска хрома удалялась гексацианоферратом (III) калия (K3[Fe(CN)6]) в течение 10 минут.

Изображение получившейся зонной пластинки показано на рис. 1.

Рис. 1. СЭМ - изображение изготовленной зонной пластинки

Численное моделирование методом FDTD

Моделирование было выполнено с помощью (FD)²TD-метода, реализованного в программном обеспечении FullWAVE (RSoft). При расчетах использовались следующие параметры сетки: шаг по пространственным координатам составил 15 нм, шаг по псевдовремени c Δ t был выбран равным 7,5 нм в соответствии с условием Куранта. В ходе анализа результатов моделирования производилось усреднение компонент поля по 10 периодам. Параметры зонной пластинки в моделировании (диаметр, фокусное расстояние, глубина рельефа) соответствовали параметрам изготовленной пластинки, но не учитывались возможные погрешности изготовления.

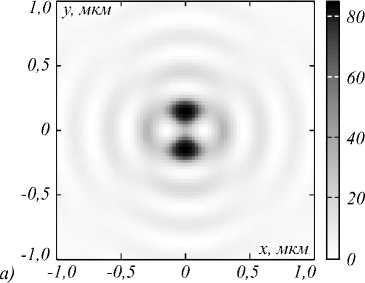
Интенсивность в фокусе рассчитывалась по формуле I = |Ex|2 + |Ey|2 + |Ez|2 = Ix + Iy + Iz, а вектор Пойн-тинга - по формуле S = Re (E* х H), где E и H - векторы напряженности электрического и магнитного по- лей в фокусе. Начальное световое поле было выбрано в виде E = (sin 2ф, cos 2ф, 0), где ф - азимутальный угол в плоскости X Y при z =0. Результаты фокусировки на расстоянии f = 532 нм показаны на рис. 2–3.

18 16

14 12

8 б

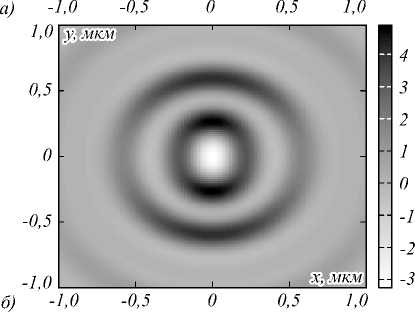
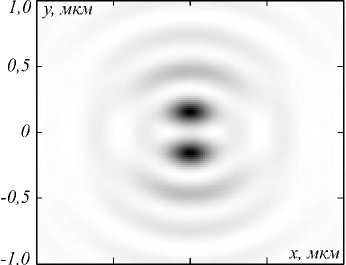
Рис. 2. Полная интенсивность (а) и продольная компонента вектора Пойнтинга (б) в фокальной плоскости

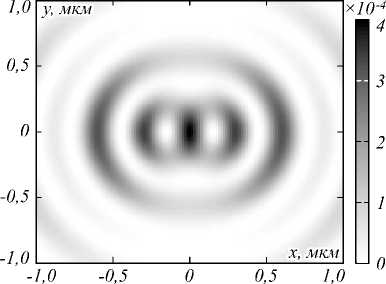
Рис. 3. Поперечная составляющая интенсивности I x +I y

Из рис. 2 и 3 видно, что распределение интенсивности и продольной компоненты вектора Пойнтинга в плоскости фокуса имеет вид колец: асимметричного в случае интенсивности (рис. 2а) и симметричного в случае с продольной компонентой вектора Пойнтинга (рис. 2б). При этом в центре кольца, формируемого продольной компонентой вектора Пойнтинга, наблюдаются отрицательные значения (обратный поток энергии). Асимметрия кольца интенсивности обеспечивается неравномерным вкладом в формирование этого кольца отдельных составляющих интенсивности – продольная составляющая формирует верхнюю и нижнюю части кольца (имеет вид двух пиков, расположенных вдоль оси y), а поперечная формирует правую и левую части кольца (имеет вид трех пиков, расположенных вдоль оси x). При этом именно поперечная составляющая интенсивности ненулевая на оси z (рис. 3).

Численное моделирование по формулам Ричардса–Вольфа

Проведем также моделирование фокусировки цилиндрического векторного пучка второго порядка (длина волны 532 нм) зонной пластинкой Френеля с помощью формул Ричардса–Вольфа [29]:

^a max ^{2 п}

U ( p , V , z ) = - if J J B ( 0 , ф ) T ( 0 ) l ( 0 ) P ( 0 , ф ) х ^X 0 0

х exp { ik [p sin 0 cos ( ф - v ) + z cos 0] } sin 0 d 0 d ф ,

где U ( p , V , z ) — напряжённость электрического или магнитного поля, B ( 0 , ф ) - электрическое или магнитное поле на входе широкоапертурной системы в координатах выходного зрачка ( 0 - полярный угол, ф - азимутальный), T ( 0 ) - функция аподизации линзы, f - фокусное расстояние, k = 2 п / X - волновое число, X - длина волны (в моделировании считалась равной 532 нм), « шах - максимальный полярный угол, определяемый числовой апертурой линзы (NA = sin a _max), l (9) - распределение входного поля в координатах выходного зрачка, P ( 0 , ф ) - вектор поляризации, для напряжённости электрического и магнитного полей имеющий вид:

линдрическим векторным пучком второго порядка в форме моды Лаггерра–Гаусса (0,1), имеющим в координатах выходного зрачка вид:

l ( 0 ) = tg ( 0 ) exp pP²

tg2 0 | v g   max

где параметр β равен отношению радиуса линзы к радиусу пучка β = R / ω. Параметр β был равен единице, что соответствует эксперименту.

Отметим, что формула (1) справедлива при фокусировке света в свободном пространстве, вдали от раздела двух сред, однако качественно результаты будут совпадать с расчетом методом FDTD. Результаты фокусировки приведены на рис. 4–5: на рис. 4 показано распределение интенсивности I = I x + I y + I z и продольной компоненты вектора Пойнтинга S z , а на рис. 5 – распределение поперечной I r = I x + I y и продольной I z составляющих интенсивности.

P ( 0 , ф ) =

1 + cos² ф ( cos 0- 1 ) sin ф cos ф ( cos 0- 1 ) - sin 0 cos ф

sin ф cos ф ( cos 0- 1 )

+

a ( 0 , ф ) +

1 + sin² ф ( cos 0- 1 ) \b ( 0 , ф ) ,

- sin 0 sin ф

где a ( 0 , ф ) и b ( 0 , ф ) - функции, описывающие состоя -ние поляризации x - и y -компонент напряжённостей фокусируемого пучка.

Для светового поля с цилиндрической поляризацией m -го порядка вектора Джонса будут иметь вид:

E ( 0 , ф ) =

^ a ( 0 , ф ) " _х ь ( 0 , ф ) _?

'" sin ⁽ m ф ) " _х cos ( m ф ) ^

для напряжённости электрического поля и

' a ^{( 0} , ф)М- cos ⁽ m ф ) " _х b ( 0 , ф)^ _х- sin ( m ф ) ^

для напряжённости магнитного поля. Вектор Пойн-тинга вычислялся по формуле S =Re ( E × H ^*). При расчете считалось, что зонная пластинка освещается ци-

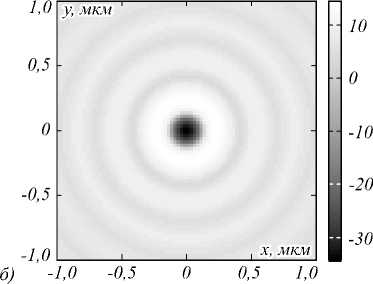
Рис. 4. Распределение полной интенсивности I = I x + I y + I z (а) и продольной компоненты вектора Пойнтинга S z (б) в фокальной плоскости

В данном случае наблюдаются качественно такие же распределения интенсивности, как и при моделировании FDTD-методом, но в распределении поперечной компоненты интенсивности центральный пик больше (рис. 5 а ), чем при фокусировке плоского волнового фронта (рис. 3). Вызвано это использованием моды Лаггерра–Гаусса (5), которая эквивалентна кольцевой апертуре. Центральная часть зонной пластинки не работает при таком освещении, а эффекты острой фокусировки усиливаются. Отметим также, что поворот исходного пучка на 90 градусов приведет к такому же повороту рис. 4 и 5 и максимумы попе-

речной составляющей (рис. 5 а ) будут расположены вдоль вертикальной оси.

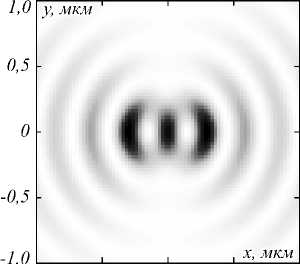
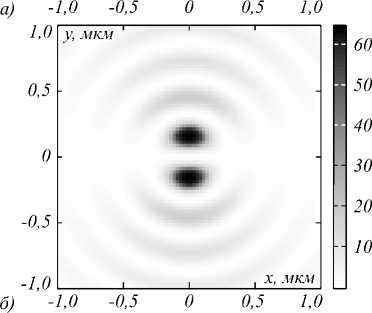
Рис. 5. Распределение поперечной I x + I y (а) и продольной составляющей интенсивности I z (б) в фокальной плоскости

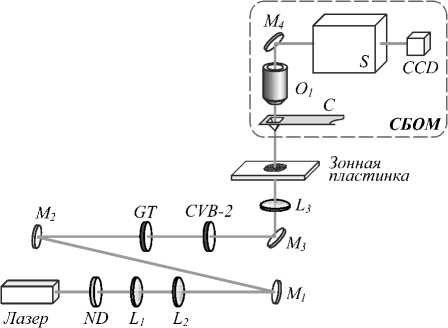
Рис. 6. Схема эксперимента. ND – фильтр нейтральной интенсивности, L 1 , L 2 , L 3 (f 1 = 35 мм, f 2 = 100 мм, f 3 = 10 мм) – линзы, M 1 , M 2 , M 3 , M 4 – зеркала, GT – поляризационная призма Глана–Тейлора, CVB-2 – преобразователь поляризации (Thorlabs WPV10-532), C – кантилевер (диаметр отверстия 100 нм, SNOM_C, NT-MDT), O 1 – 100× объектив (100X Mitutoyo Plan Apo Infinity Corrected Long WD Objective), S – спектрометр (Solar TII, Nanofinder 30), CCD-камера (Andor, DV401-BV)

Эксперимент средствами сканирующей ближнепольной оптической микроскопии

С помощью сканирующего ближнепольного микроскопа СБОМ Интегра Спектра изучалась фокусировка цилиндрического векторного пучка второго порядка. Схема эксперимента показана на рис. 6.

Кантилевер СБОМ имеет вид полой пирамидки из тонкого слоя алюминия с отверстием на вершине. Диаметр отверстия составляет около 100 нм. Попере-ченое сканирование области фокуса осуществлялось с точностью 35 нм.

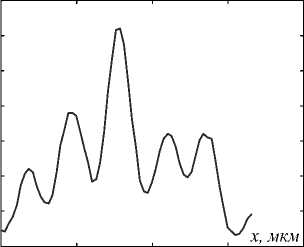
Измерения на СБОМ показали, что распределение интенсивности в фокусе имеет пиковый характер. Пример распределения интенсивности в фокусе (на расстоянии 0,6 мкм от поверхности) и его сечения показаны на рис. 7.

у, Л1КЛ1

X, Л1КЛ1

• а)  О 0,5      1,0      1,5

  
  
  

Интенсивность, отн.ед.

• б)    О 0,5       1,0       1,5      2,0

Рис. 7. Распределение интенсивности в фокусе, измеренное на СБОМ (а), и его сечение вдоль оси x (б)

Размеры фокусного пятна на рис. 7 составили FWHMx=0,39λ и FWHMy=0,71λ.

Из сравнения рис. 3, 5 а и 7 видно качественное согласование результатов, полученных на СБОМ (рис. 7), с распределением поперечной составляющей интенсивности светового поля Ix + Iy в моделировании (рис. 3 и 5 а ). Хотя в численном моделировании боковые пики вдоль оси y получились более выраженными, чем в эксперименте.

Заключение

В данной работе рассмотрена фокусировка цилиндрического векторного пучка второго порядка амплитудной зонной пластинкой Френеля с фокусным расстоянием 532 нм и диаметром 15 мкм, изготовленной средствами электронной литографии, химического травления и лифт-офф процесса в алюминиевой пленке толщиной 50 нм. Численно было показано, что такая зонная пластинка формирует в фокусном пятне на оси область, в которой направление вектора Пойнтинга противоположно направлению распро- странения пучка (область обратного потока энергии), а поперечная составляющая интенсивности ненулевая на оптической оси и имеет вид трех пиков, расположенных вдоль оси x. Область обратного потока исследовалась с помощью сканирующего ближнепольного оптического микроскопа Интегра Спектра (НТ-МДТ) на основе полого пирамидального апертурного кантилевера. Экспериментально фиксировалось пиковое распределение интенсивности в фокусе (с субволновыми размерами    FWHMx=0,39λ    и

FWHMy=0,71λ). Сравнение распределений интенсивности, детектируемой СБОМ кантилевером, и характеристик светового поля, рассчитанных с помощью метода FDTD и формул Ричардса–Вольфа, позволяет говорить о чувствительности кантилевера к поперечной составляющей интенсивности, а не суммарной интенсивности или компонентам вектора Пойнтинга в области обратного потока энергии.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение» и «Заключение», Российского научного фонда (грант № 18-19-00595) в части «Эксперимент средствами сканирующей ближнепольной оптической микроскопии», Российского фонда фундаментальных исследований РФФИ, (грант № 18-07-01380) в части «Дизайн и изготовление зонной пластинки», (грант № 18-29-20003) в части «Численное моделирование методом FDTD».