Поперечные колебания круглого биморфа с пьезоэлектрическим и пьезомагнитным слоями

Funding information: the research is done with the support from the RF Ministry of Education and Science (project part of state order no. 9.1001.2017/ПЧ) and the Government of the Russian Federation (contract no. 075-15-20191928).

Введение. В создании сенсорных и измерительных систем, современной малогабаритной бытовой техники, телефонов сотовой связи и беспроводных сенсорных систем для наблюдения и диагностики технического состояния различных объектов не требуются мощные источники энергии, однако мобильность и энергонезависимость вышеперечисленных устройств являются обязательными. Устройства накопления энергии с пьезоактивными элементами, прямо преобразующими энергию механических колебаний в электрическую энергию, широко применяются для питания такого рода аппаратов. В [1–3] исследованы устройства накопления энергии с использованием пьезоэлектрических генераторов при воздействии механических нагрузок.

Если система находится в переменном магнитном поле, созданном постоянными магнитами, установленными на вращающихся деталях машины, то пьезомагнитный слой деформируется вместе с пьезоэлектрическим элементом. За счет этого происходит образование электрического тока. Guo-Liang Yu и др. в [7, 8] обсуждали теоретические модели многослойных магнитоэлектрических композитов для магнитоэлектрического отклика на резонансных частотах, соответствующих колебаниям изгибной и экстенсиональной моды. Теоретическая модель магнитных энергетических собирателей, использующих функционально-градиентный композитный кантилевер, проанализирована для улучшения собирающей способности и регулировки резонансной частоты в [9]. В [10] Y.F. Zhanga и др. изучали бифуркации, периодическую и хаотическую динамику четырехгранной композитной многослойной пьезоэлектрической прямоугольной пластины с простыми опорами. В [11] изучались изгибные и свободные колебания магнитоэлектроупругой пластины с поверхностными эффектами.

В настоящей работе рассматриваются осесимметричные колебания устройства. Изучено влияние радиуса и толщины пьезоэлектрической и пьезомагнитной пластин на частотные характеристики устройства (собственные частоты резонанса и антирезонанса) и на эффективность преобразования энергии колебаний в электрическую энергию, которая характеризуется коэффициентом электромеханической связи. В качестве метода решения задачи выбран метод конечных элементов, реализованный в пакете ANSYS.

z - ось симметрии

Г

u_r=0     ■ Пьезомагнетная пластина

τ ^rz           Металлическая пластина

Рис. 1. Схема половины осевого сечения пьезомагнитоэлектрического генератора

Механика

Рассматриваемое устройство накопления энергии представляет собой осесимметричную конструкцию, которая состоит из металлического диска (подложка) с наклеенными на него двумя пьезоактивными слоями (рис. 1). Верхний слой — пьезоэлектрический, нижний — пьезомагнитный. Плоские поверхности пьезоэлектрического слоя покрыты электродами, которые подключены к внешней электрической цепи или один из электродов свободен, а на другом задан нулевой электрический потенциал. На пьезомагнитный слой действует переменное магнитное поле по гармоническому закону, внешний радиус подложки шарнирно закреплен. Математической моделью поперечных установившихся колебаний описанной конструкции является краевая задача линейной теории пьезомагнитоэлектроупругости [4]. В качестве инструмента решения выбран пакет ANSYS, в котором реализована модель пьезоэлектричества.

Краевая задача для пьезомагнитоэлектрического тела состоит из системы уравнений и граничных условий [4]:

• V-о + рf = р и, V-D = оп, V-B = 0(1)

о = c : е - e - E - h - H

D = e: е + к - E + a - H(2)

B = h : е + aT - E + д - H е = , (vu + (Vu)T), E = -Vф, B = -Vф,(3)

где о и е — тензоры механических напряжений и деформации; D и E — векторы электрической индукции и напряженности электрического поля; B и H — векторы магнитной индукции и напряженности магнитного поля; р — плотность материала; c — тензор упругих модулей; e — тензор пьезоэлектрических модулей; h — тензор пьезомагнитных модулей; к — тензор диэлектрических проницаемостей; a — тензор магнитоэлектрических модулей; д — тензор магнитных проницаемостей; f — вектор плотности массовых сил; о_п — объемная плотность электрических зарядов; u — вектор перемещений; ф и ф — электрический и магнитный потенциалы.

Граничные условия задаются для механических, электрических и магнитных компонент полей.

Механические граничные условия. Пусть поверхность 5 состоит из двух частей Г , и Г ₂, так что 5 = Г , и Г ₂, причём Г , п Г ₂ = 0 .

• u = U на Г,, n - о = p на Г2.(4)

Электрические граничные условия. Пусть поверхность 5 состоит из двух частей Г ₃ и Г ₄, так что 5 = Г ₃ и Г ₄, причём Г ₃ п Г ₄ = 0 .

ф = ф(x, t) на Г3, n - D = -о0 на Г4,(5)

где о ₀ — плотность поверхностных зарядов. Кроме того, в случае если электроды подключены к внешней цепи, необходимо добавить два условия:

ф|S = v, JJ n - DdS = I,(6)

E где sE — площадь электрода; v — неизвестный потенциал, который находится из второго условия; I — электрический ток.

Магнитные граничные условия. Пусть поверхность 5 состоит из двух частей Г ₅ и Г ₆ , так что 5 = Г ₅ и Г ₆, причём Г ₅ п Г ₆ = 0 .

ф = ф ( x , t ) на Г ₅, n - B = о , на Г ₆                                         (7)

где о , — плотность поверхностных свободных токов вдоль границы.

Для упругого слоя используются первые уравнения в системе (1)-(3), неизвестными являются компоненты вектора смещений u , для пьезоэлектрического к ним добавляются вторые уравнения, неизвестны u и электрический потенциал ϕ , а для пьезомагнитного к первым уравнениям добавляются третьи и к неизвестным смещениям — магнитный потенциал ф . При этом соотношения (2) преобразуются обнулением соответствующих констант.

Конечно-элементное моделирование. Компьютерная модель устройства построена в конечноэлементном пакете ANSYS. Металлическая подложка (сталь) имеет толщину h и радиус г. Пьезоактивные слои состоят из одной пьезокерамической и одной пьезомагнитной пластин, которые поляризованы по толщине, имеют толщину h_p и радиус г_р (рис. 1).

В конечно-элементной модели устройства для металлического и пьезоэлектрического слоев используются в качестве конечных элементов PLANE42 и PLANE13 соответственно. В этой работе пьезомагнитный слой моделируется конечным элементом PLANE13, в котором пьезоэлектрические свойства материала заменены на пьезомагнитные. Это возможно сделать по двум причинам: пьезослои между собой не контактируют, качественно уравнения для электрического и магнитного потенциалов совпадают.

Свойства пьезоактивных слоев, используемые в расчетах, представлены в таблицах 1–2: пьезокерамика — PZT-4, пьезомагнитный материал — CoFe2O4 [5, 6], клеевые слои не учитываются.

Таблица 1 Материальные свойства пьезокерамики PZT-4

С 1 E 1 , Гпа	С 1 E 2 , Гпа	С 1 E 3 , Гпа	С 3 E 3 , Гпа	С 4 E 4 , Гпа	e 31 , Кл/м2	e 33 , Кл/м2	e 15 , Кл/м2	k 11 / ε 0	k 33 / ε 0
139	77,8	74,3	115	25,6	–5,2	15,1	12,7	730	635

Здесь ε ₀ = 8, 85 × 10 ^{- 12} Ф/м, плотность пьезокерамики PZT-4 ρ = 7500кг/м³.

Таблица 2

Материальные свойства пьезомагнитного элемента CoFe2O4

M С 11 ,	M С 12 ,	M С 13 ,	M С 33 ,	M С 44 ,	Q 31 ,	Q 33,	Q 15,	λ 11 ,	λ 33 ,
Гпа	Гпа	Гпа	Гпа	Гпа	Н/А м	Н/А м	Н/А м	Н с2/Кл2	Н с2/Кл2
286	173	170	269,5	45,3	580,3	699,7	550	5,9x10-4	1,57x10-4

Плотность пьезомагнитного элемента CoFe₂O₄ ρ = 5290 кг/м³.

Упругие свойства изотропного материала подложки характеризуются модулем Юнга E и коэффициентом Пуссона ν , в расчетах использовались E = 200 ГПа, ν= 0,29 , плотность ρ = 7860 кг/м³ (сталь).

Для достижения высокой точности в расчетах размер конечного элемента металлической слоя установлен значением не выше 15 его толщины, размер конечного элемента пьезослоев автоматически установлен. Сетка конечных элементов устройства накопления энергии представлена на рис. 2.

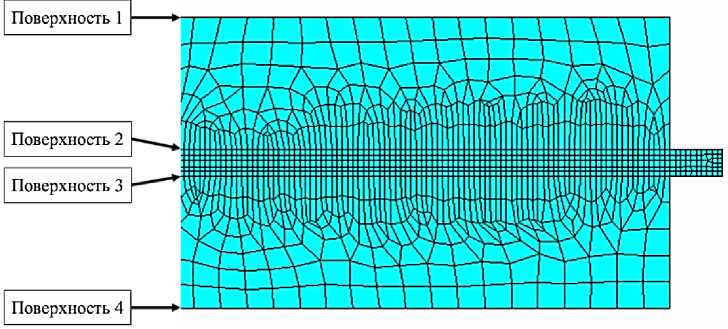
Рис. 2. Сетка конечных элементов устройства накопления энергии.

Поверхности 1, 4 — внешние поверхности пьезослоев; поверхности 2, 3 — контактные поверхности между пьезослоями и металлическим слоем

При анализе собственных колебаний пьезоэлектромагнитного устройства накопления энергии предполагается выполнение следующих механических и электромагнитных граничных условий. На левом конце заданы условия симметрии, правый конец шарнирно закреплен (рис. 1). Для вычисления частоты резонанса устройства электрические потенциалы заданы на поверхностях 1, 2; на поверхности 3 задан магнитный потенциал; плотность магнитного потока задана на поверхности 4. В случае вычисления частоты антирезонанса устройства на поверхностях 1–4 заданы такие же граничные условия, как для вычисления частоты резонанса. Однако электрический потенциал на поверхности 1 неизвестен и находится из условия (6).

Численные результаты . Рассматриваются собственные колебания пьезоэлемента, радиус которого составляет r p =9,8 мм, толщины пьезослоев h p =0,5 мм, радиус подложки r=10 мм, толщина подложки h=0,1 мм. В таблице 3 представлены первые три собственные частоты антирезонанса.

Механика

Таблица 3

№

Частота антирезонанса, кГц

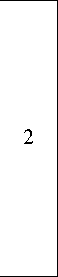
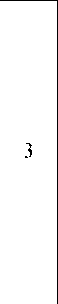
11,675

56,748

115,572

Собственные частоты антирезонанса

Распределение вертикального смещения на деформированном состоянии и распределение электрического и магнитного потенциала на недеформированном образце

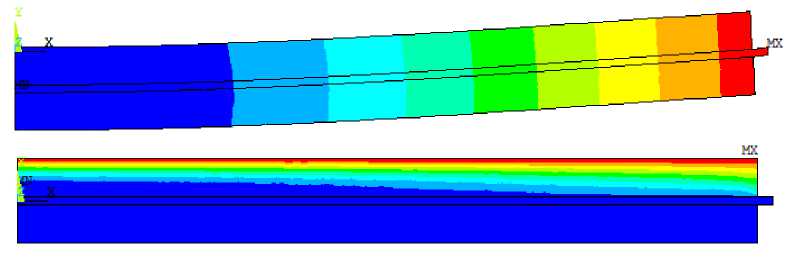
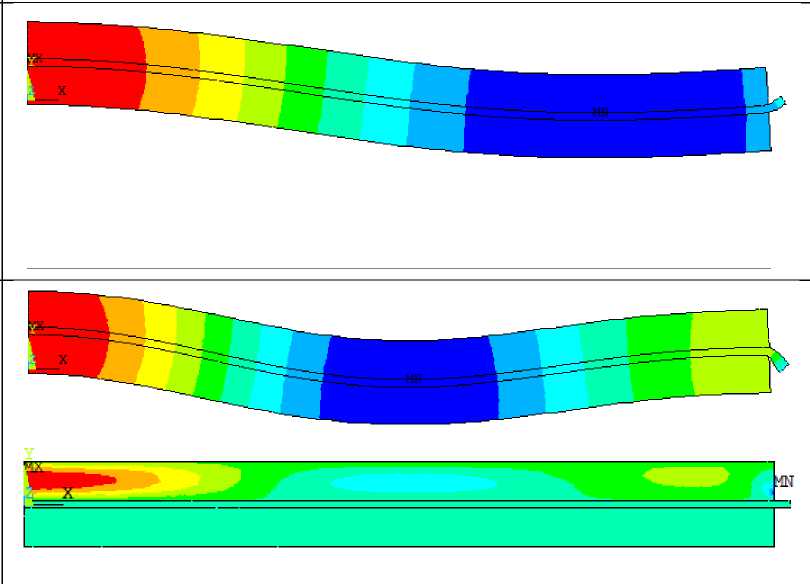
В таблице 3 представлены распределения вертикального смещения, электрического и магнитного потенциала, при этом последние представлены в единой шкале, поэтому отображение магнитного потенциала не является наглядным. Для построения приближенной теории расчета колебаний рассмотренного биморфа, проведен анализ напряженно-деформированного состояния, электрического и магнитного полей, который показывает, что для низших изгибных мод могут быть принятые гипотезы об их распределении, соответствующие изгибу пластин.

В представленных ниже результатах численных расчетов исследуется зависимость собственных частот резонанса и антирезонанса, коэффициента электромеханической связи от геометрических параметров.

Когда число чередующихся пьезоэлектрических и пьезомагнитных слоев становится достаточно большим, возможно использование подхода на основе эффективных свойств пьезомагнитоэлектрического композита [5, 6]. В этом случае используются все уравнения задачи (1-3).

Значение толщины пьезослоев h p изменяется в пределах 0,3^0,7 мм, а радиуса rp — в пределах 6,8^9,8 мм.

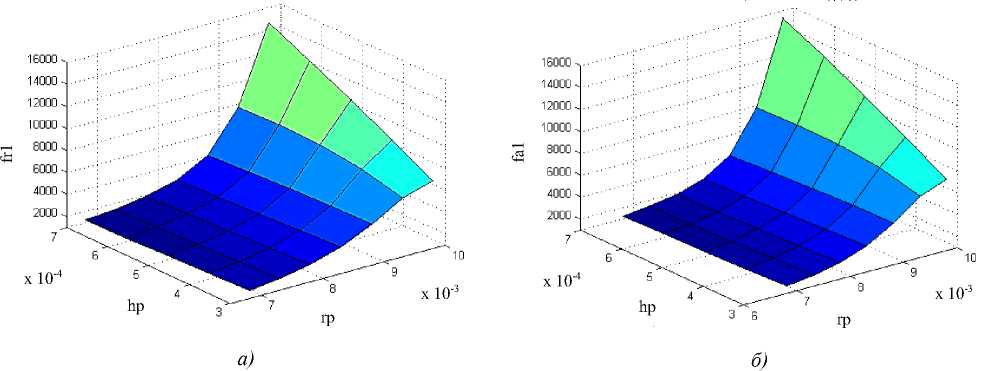
Рис. 3. Собственные частоты: а — частота резонанса, б — частота антирезонанса

На рис. 3 представлены зависимости собственной частоты от значения толщины hp и радиуса rp пьезослоев. Из рис. 3 видно, что значения собственных частот возрастают с увеличением радиуса.

На рис. 4 представлена зависимость коэффициента электромеханической связи от значения толщины h_p и радиуса r p пьезослоев. Из рис. 4 видно, что значение собственной частоты возрастает с ростом радиуса пьезослоев r p , но убывает с ростом толщины пьезослоев h p .

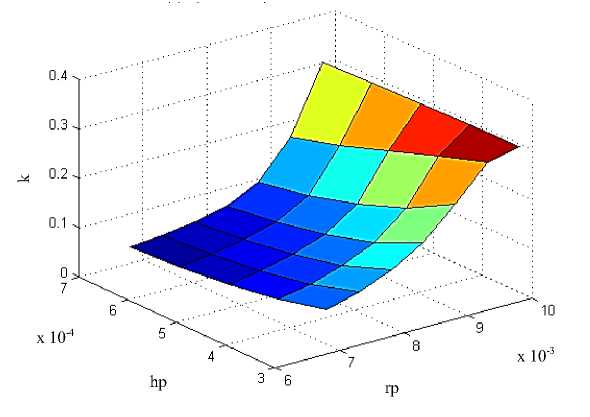
Рис. 4. Коэффициент электромеханической связи

Заключение . В работе рассматривается осесимметричная конечно-элементная модель устройства накопления энергии на основе круглых пластин в пакете ANSYS. Активными элементами устройства накопления энергии являются пьезоэлектрическая и пьезомагнитная пластины, закреплённые на металлической пластине. Исследовано влияние геометрических характеристик пьезослоев в условиях определенных ограничений на размеры устройства, на коэффициент электромеханической связи, который показывает эффективность устройства накопления энергии. Результаты расчетов, приведенные в работе, позволяют выбрать рациональные размеры пьезоэлементов, работающих на определенной частоте и имеющие наибольшую эффективность. Данный анализ показывает, что максимальное значение коэффициента электромеханической связи достигается, когда толщина и радиус пьезослоев соответственно принимают наибольшее и наименьшее значения в рассматриваемых пределах.

Механика