Поперечные колебания пластины, податливой при трансверсальном сдвиге

Композитные конструкции, обладающие высокой степенью весового совершенства, часто используются в производстве космической техники. Композитные пластины отличаются низкой сдвиговой жесткостью по отношению к трансверсальным напряжениям. Учет указанной особенности при реализации численного расчета приводит к повышению порядка разрешаю- щих уравнений за счет введения в рассмотрение углов трансверсального сдвига.

Разрешающие уравнения теории метода конечных элементов (МКЭ) для задачи о собственных колебаниях пластины с низкой трансверсальной сдвиговой жесткостью получим вариационным способом. Для этого запишем выражение полной энергии колеблющейся пластины

~    ~   ~

E = U + T ,

где U – потенциальная энергия деформации; T – кинематическая энергия движения.

Выражение для потенциальной энергии деформации пластины как трехмерного тела имеет вид

~    1 r r - -    - -- -

^U = ?J J J ^{( П} xex ^{+ 6} yeУ ^{+ 6} zez ⁺

2 (V)(2)

+t„,e„+ t,e„ + т, e dxdydz, xy xy xz xz yz yz, где напряжения и деформации являются функциями координат и времени

6 = 6(x, у, z, t) ;     e = e(x, y, z, t),(3)

„   6 z	6 x	6 у	= т xy
e =-- z	" Ц zx” Е	— Ц zy — ; exy E y	” G
z	x		xy
	т„	т
	Уz .	XZ
e		e = —,
yz	Gyz ;	xz Gxz

где Е x ( y , z ) – модуль упругости соответствующего направления; G xy ( yz , xz ) – модуль сдвига в соответствующей плоскости; μ xy , μ yx , μ yz , μ zy , μ xz , μ zx – коэффициенты Пуассона.

Имеет место свойство симметрии упругих постоянных:

Ex Ц xy = ^Еу Ц yx ;   ^Еу Ц у _г = ^Ez Ц zy ;   Ex Ц xz = ^Ez Ц zx .   ⁽¹²⁾

где 6 - любой параметр из 6Х,6У,6Z,тм,т„т; x y z xy yz xz e – любой параметр из ex,ey,ez,exy,eyz,exz .

Геометрические соотношения имеют вид

Используя принятые в [1] допущения, выражение потенциальной энергии деформации (2) можно привести к виду

L J = U sin² to t ,                  (13)

e _x

д йх   _   д u у x ; e = у ; e дx    у   ду    z e .^ + ■■;

yz   д z    д у

д й   _   д йх  д йу z_; е = x +у ;

дz        дуд д йх д й x ^+ z   дzд

где U определяется выражением

1 г г г f (д й     дб_х )      Г д v    ^д6_у )

U =- М6 _x l+ z^x 1 + 6     + z^у 1 +

2^J₍ v ) l 1д x      д x )     ^у (д у     д у )

где й _x , й _у , й _z - проекции перемещения произвольной точки на соответствующие оси координат. Они также являются функциями координат и времени:

^{+ Т} xy

д й д v   Г д9_г

+   + z I x + ду дx   ( ду

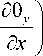
^{+ т} xz V x ^+т yz V у } ^dxdУ^dz .

г? x = йx ( x , у , z , t );     й у = йу ( x , у , z , t );

г? z = г? z ( x , у , z , t ).                       (5)

Выражение кинетической энергии колебания пла-

стины имеет вид

При гармонических колебаниях закон изменения перемещений по времени можно представить в следующем виде:

й _x = й_х sin to t ; й _у = й _у sin to t ; й _z = u _z sin to t , (6)

^T = ¹ J J J ( ^?x ^{2 +} 1^у ⁺ i^z ² ) р ^dxdУ^dz ,         ⁽¹⁵⁾

2 ( V )

где ω – круговая частота колебаний, а перемещения u x , u y , u z зависят только от координат:

ux = ux ^{( x} , у , ^z ); ^йу = ^йу ^{( x} , у , ^z ); uz = uz ^{( x} , у , ^z )- ⁽⁷⁾

Подставляя (5) в (4), получим:

e = e sin to t ,                          (8)

где e – любой параметр из e x , e y , e z , e xy , e yz , e xz , для которых справедливы геометрические соотношения

где ρ – плотность материала (в общем случае является функцией координат); - v _x , -р_у , -р _z - проекции вектора скорости на соответствующие оси координат, связанные с перемещениями дифференциальными зависимостями

v _x

^д u ? x .

д t ’

vy

дй^. д t ’

v _z

д Uz д t

В

дй,        дйу        д uz         д йх   дй, x_; е =   у_ ; e =       ; e =     +      ;

д x         д у       д z         д у    д x

дй   дй, е = —- +--- ; e уг    дz    ду    xz

д й_х дй, = —- + —-.

д z

д x

Подставляя (5) в (16), а затем результат – в (15), получим

T = T cos² to t ,                  (17)

где

T = —J J J ( ?x + ?у + uz 2 ) pto ² dxdydz .       (18)

2 ( V )

силу линейности физических

соотношений

можно записать

Приравнивая максимальные значения потенциальной и кинетической энергии, которые определяются выражениями (14) и (18), получим

6 = 6 sin to t ,

где σ – любой из параметров σ x , σ y , σ z , τ xy , τ yz , τ xz , для

которых справедливы физические соотношения

1 г r r f Г д u д0 ) Г д v д0 _у ^ —    <6 _x I— + z— ^x 1 + 6 _x I— + z —- 1 +

2 (V ) l (д x д x ) (д у д у J

e _x

⁶ x

—

Ex

Ц xy

6 y

Ey

—

Ц xz

⁶ z .

Ez

ey

⁶ у

Ey

^{— Ц} yx

⁶ x

Ex

^{— Ц} yz

⁶ z

Ez

^{+ Т} xy

д й д v   Г д0_г

++ z I ^x + д у д x   ( д у

д0 у ) д x J

^{+ т} xz V x ^+т yz V у } х

x dxdydz —J j jp® ² [ ( u + z 6_X ) 2 + 24?    ^{LX      x/}

+ ( v + z 9 _y ) + w ² ] dxdydz = 0.

При выводе (19) учтено, что u_ = u + z9, ; u„ = v + z9„ ; u, = w, x             xy             yz

где u и v – перемещения точек начальной плоскости вдоль осей X и Y соответственно; w – прогиб точек начальной плоскости; θ x , θ y – углы наклона сечения,

определяемые соотношениями

9 x = V x

d w

—

d x

;

⁹ y = V y

d w

—

d y

.

Проинтегрируем (19) по толщине пластины, т. е. по координате z в пределах от –s до h – s . В результате преобразований получим

1 ^ab

^ J J V x x У У xy xy      x ^X x

^{+ M}y X y ^{+ M}xy X xy ^{+ Q}x V x ^{+ Q}y V y ) ^dX^dy —

ab

^— t®² JJ { B p ( ^u 2 ^{+ v 2 + w 2} ) ⁺             (²²⁾

2   00

+ 2 C p

^u \ V x

8 w )  f

— 1+ v l V

8 x J   (

y

+

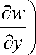
d9y        d9

x =   -; x =+-.

y dy   x"^   dy

В итоге с учетом (21) получим

ab

И l-fd u

0 0 I ⁽ x-^

2                          2 ²

d u I dv, d w I _ I dv, d w 1

+ 2C11— \ i-x--- I+D„|—2-1 + dx ( dx dx2 J ( dx   dx2 J

d u d v     d u ^{f dv} y d ² w Y    5 v ^f dv x

+ 2 B₁₀ Г 2C-1                 + 2C3

d x d y       d x ^ d y   d y J     d y ( d x

+   ^fd V x ^d 2 ^w Y^ у ^d 2 w

+ 2 D ,2 l---— Il---— I+ B 22

( d x   d x ² J( d y    d y J

+ 2 C 22 8 ^ I ' ^V d y ( d y

d ² w

—

8 y ²

( dV„

+ D 22 —

²² ( d y

—

+ B 33 l A ⁺ A I ^{+ 2 C} 33 (d y d x J

⁺ D 33

ab

—m 2 ff

d ² w )

l x ²" J+

I ⁺ d y J

d ² w Y

—

8 y ²

8 u 8^v ^Tdv x ^dv y    a² w I

— + — Il —— + —-- 2— 1 +

d y 8 x

d x

S y

8 x 8 y

dV x +^ _{— 2} d ² w | 2

8 x

d y

8 x d y

⁺ Kx V 2 ⁺ Ky V 2 } dxdy ^—

u ² + v ² +

+ d p

w ² ) + 2 C p u |v x

d w 1 2 f

^V x a. ⁺ \ ^V y ^—

d w | I

—^-i+ v \ V y —

d w ) 2

d y

dxdy = 0.

d w

d y

+

D p

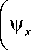
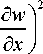
⁺ | V y

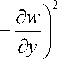
- dxdy = 0.

Здесь N , M , Q – внутренние погонные усилия, определяемые следующими соотношениями:

Nx = ^B 1i ^e x ^{+ B} 12 ^S y ^{+ C} 11 ^X x ^{+ C} 12 ^X y ;

Ny = B 21 ® x + B 22 ^ y + C 21 X x + C 22 X y ;

Nxy = B 33 Е xy + C 33 X xy ; Qx = Kx V x ; Qy = Ky v y ;

Mxy = C 33 S xy + D 33 X xy ;            (23)

Mx = C 11 S x + C 12 S y + d „x x + D 12 X y ;

My = C21Sx + C-y + D21Xx + D22Xy , где B, C, D и K – параметры мембранной, смешанной, изгибной и трансверсальной жесткости соответственно; Bρ, Cρ, Dρ – параметры инерции пластины, вычисляемые по формулам h—s                  h—s                       h—s

B p = J P dz ; C p = J p zdz ; D p = J p z ² dz • (24)

— s                   — s                        — s

Сделаем последние преобразования в функционале (22). Приведем его к виду, удобному для реализации КЭ процедуры. Для этого с помощью физических соотношений (23) выразим усилия через деформации, которые также выразим через перемещения и углы трансверсального сдвига с помощью геометрических соотношений du       8 v       8 u 8 v       d9r s x =7-; s y = 7-; s xy ,-,; x x = -7-;

8 x       d y        8 y 8 x        8 x

Функционал (26) позволяет получить разрешающие уравнения для задачи о свободных колебаниях пластины.

Выполним модальный расчет пластины с помощью МКЭ. Будем рассматривать четырехузловой конечный элемент пластины, для которого вектор узловых кинематических параметров имеет вид

δ е ={ δ 1 δ 2 δ 3 δ 4 } ^Т ,              (27)

где δ i ( I = 1, 2, 3, 4) – вектор неизвестных i -го узла

T

I     fd w 1 fd w 1                      I

8 / = ( w \ I \ I V xi V yi u ^vi - . ⁽²⁸⁾ d x Id y

Кинематические переменные внутри элемента представим следующим вектором

J   dw dw1

8 = 1w             Vx Vy u v - .

Id

Его компоненты определяются через узловые значения (28) с помощью соотношения

δ = P δe,(30)

где P – матрица размерностью 7 × 28. Это так называемая матрица функций формы.

Подставим выражения для компонент вектора δ (29) в функционал (26), выполним интегрирование по площади элемента, в результате получим функцию полной энергии колебания конечного элемента пластины. Эта функция зависит от компонент вектора узловых кинематических параметров (28), минимизация по которым приводит к системе однородных алгебраических уравнений:

K e δ e – ω ² S e δ e = 0 ,               (31)

где K_e – матрица жесткости; S_e – матрица инерциальных параметров конечного элемента пластины (обе – симметричные, размером 28×28).

В выражениях для компонентов матрицы K_e фигурируют параметры жесткости, а в выражениях для компонентов матрицы S_e – параметры инерции. Например:

• 2    14 D 33 a² b ² + 5 D ₁₂ b² a ² +10 D 11 b ⁴ + 10 D ₂₂ a⁴ _ k 11 = 7                       373                      ^;

• 5                         a ³ b ³

• 1    727 B _p b ² a ² + 5 520 D _p b ² + 5 520 D _p a ²

^{5 11} =                12 600 ab               "

Если структура пакета пластины симметрична относительно срединной плоскости и система координат связана со срединной плоскостью, то в этом случае смешанные жесткости пластины C и инерционный параметр C _ρ становятся равным нулю, и структура матрицы инерции упрощается за счет появления в ней множества нулевых компонентов.

Представим матрицу жесткости и матрицу инерции конечного элемента пластины в блочном виде:

толщина пластины h = 3 мм, модуль упругости E = 210 ГПа, коэффициент Пуассона μ = 0,3, плотность ρ = 7 800 кг/м ³ .

В результате расчета, выполненного по нашей модели с двадцатью элементами вдоль каждой из сторон пластины, определены первые пять значений собственных частот (табл. 1) и соответствующие им формы колебаний. Здесь в качестве формы колебаний будем рассматривать распределение функции прогибов. Для оценки полученных результатов выполнен расчет в пакете COSMOS/M, где для моделирования использованы элементы тонкой оболочки SHELL4.

Таблица 1

Значения частот собственных колебаний

Номер моды	Частоты собственных колебаний, Гц
	Тестируемое решение	Решение COSMOS/M
1	26,908	26,976
2	54,831	55,017
3	54,831	55,017
4	80,483	81,112
5	98,287	98,630

	┌│ K I–I	K I–II	K I – III	K I – IV
	│ K II – I	K II – II	K II – III	K II – IV
K e =	│ K III–I	K III–II	K III – III	K II – IV
	│ K IV – I	K IV – II	K IV – III	K IV – IV

Результаты модального расчета, выполненного с помощью нашей модели (рис. 1), имеют хорошее совпадение с решением в пакете COSMOS/M (рис. 2). Это касается и частот собственных колебаний (см. табл. 1) и форм мод (рис. 3–6).

	┌ │ S I – I	S I – II	S I – III	S I – IV
	│ S II – I	S II – II	S II – III	S II – IV
S e =	│ S III – I	S III – II	S III – III	S III – IV	│;     (32)
	│ S IV – I └	S IV – II	S IV – III	S IV – IV

где K_i– j и S_i– j ( i,j = I, II, III, IV ) – подматрицы размером 7 × 7. Ненулевые компоненты этих матриц определяются теми же выражениями, что и соответствующие компоненты матриц жесткости и инерции, фигурирующих в уравнениях системы (31).

Глобальная система разрешающих уравнений в задаче модального расчета пластины имеет вид

K Σ Δ – ω ² S Σ Δ = 0 ,          (33)

где Δ – глобальный вектор узловых неизвестных, Δ = { δ 1 δ 2 … δ i … δ N } ^Т ,              (34)

где N – общее число узлов в системе; K _Σ – глобальная матрица жесткости; S _Σ – глобальная матрица инерции. Система (33) в математическом смысле является обобщенной задачей на собственные значения, решая которую (после учета в ней граничных условий), определим частоты и формы собственных колебаний пластины.

Протестируем полученный алгоритм решения на примере модального расчета изотропной квадратной пластины, жестко защемленной по контуру. Зададим следующие размеры пластины и механические свойства материала: длина стороны пластины a = b = 1 м,

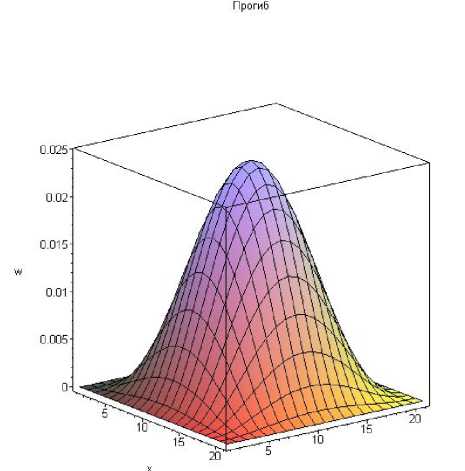
Рис. 1. Форма колебаний, соответствующая первой собственной частоте

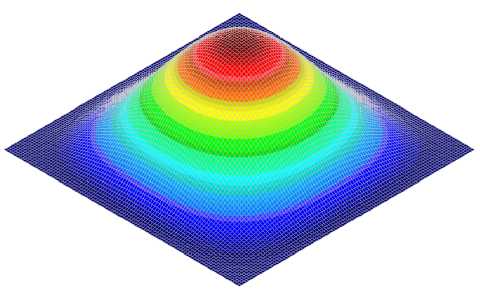
Рис. 2. Форма колебаний, соответствующая первой собственной частоте (COSMOS/M)

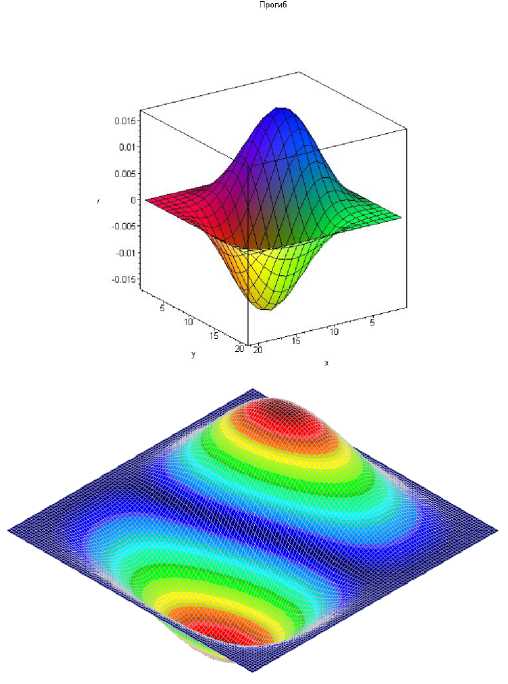
Рис. 3. Форма колебаний, соответствующая второй собственной частоте

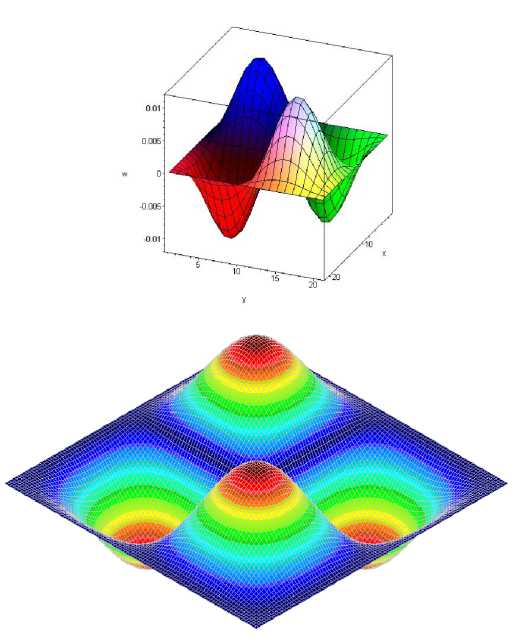
Рис. 5. Форма колебаний, соответствующая четвертой собственной частоте

Выполним численное исследование влияния вида граничных условий на величины частот собственных колебаний квадратной композитной пластины. Будем сравнивать два вида защемления: классическое (I) и со свободным сдвигом (II). Примем длины сторон пластины a = b = 1 м, а ее толщину h = 10 мм.

Будем полагать пластину изготовленной из однонаправленного композита с углами укладки φ = ±45 ^о . Зададим следующие механические свойства (углепластик):

– модуль упругости вдоль волокон E 1 = 180 ГПа;

– модуль упругости поперек волокон E ₂= 6,2 ГПа;

– модуль сдвига G 12 = 5 ГПа;

– коэффициент Пуассона μ 12 = 0,007;

– плотность ρ = 1 500 кг/м ³ .

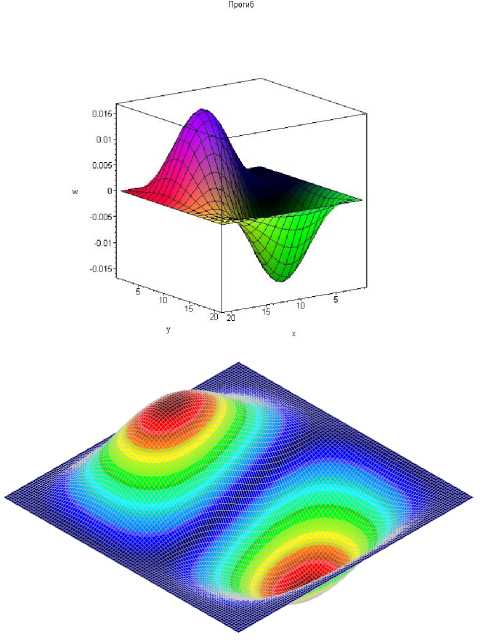
Рис. 4. Форма колебаний, соответствующая третьей собственной частоте

Прогиб

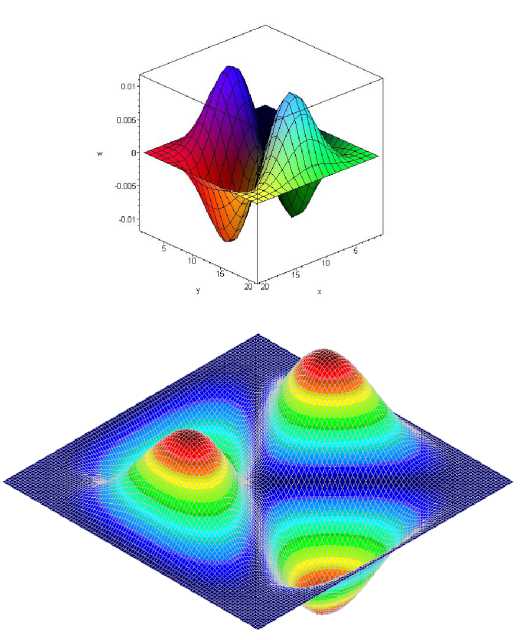
Рис. 6. Форма колебаний, соответствующая пятой собственной частоте

Упругие параметры пластины, которую будем считать однослойной и условно однородной, вычислим по формулам

A₁₁ = E₁ cos⁴ ф + E 2 sin⁴ ф + 2 ( Е 1 ц ₁₂ + 2 G ₁₂ ) sin² ф cos² ф ;

A 2 = E₁ sin⁴ ф + E ₂ cos⁴ ф + 2 ( E₁ ^ ₁₂ + 2 G ₁₂ ) sin² ф cos² ф ;

A2 = A1 = ^2 +(Ei + E2 - 2 (E1M12 + 2G12)) sin2 ф cos2 ф; A33 = (E1 + E2 - 2 E1^12) sin2 ф cos2 ф + G12 cos2 2ф, где E1 и E2 – приведенные модули упругости, вычисляемые по формуле

E 1(2)

E 1( ² )             и ,

1  ^ 12 ^ 21

а коэффициент Пуассона μ 21 определяется из условия симметрии упругих постоянных:

^ 21

Н 12 E 1

E 2

Модули трансверсального сдвига примем равными G 12 .

Коэффициенты жесткости пластины вычислим по формулам

B 11 = 41 h ; B 22 = A 22 h ; B 21 = A 21 h ;

	= A 33 h ;	A h 3		A 22 h 3
		11	D
B 33		11        12 ;	D 22	12 ;
D 12	A 12 h 3	. D = A 21 h3	; D 33	A 33 h 3
	12	;    21      12		12

Kx = Ky = G 12 h ;

Cij = 0    (ij = 11, 22, 12, 21, 33), а параметры инерции – по формулам

B ρ = ρh ; C ρ = 0 ; D ρ = ρ h ³ /12

Результаты вычислений в виде значений первых пяти частот собственных колебаний поместим в таблицу (табл. 2). Здесь же приведены частоты для пластин с толщинами 30 и 50 мм.

Формы колебаний соответствуют тем, что приведены на рис. 2–6.

Анализ представленных результатов говорит о том, что в задаче модального расчета результаты, полученные при защемлении со свободным сдвигом краев, отличаются от тех, что определены при классическом защемлении. Это различие нарастает по мере увеличения толщины пластины, достигая максимума (по первой частоте) в рассматриваемой модели в 10,6 %.

Проведенная работа позволяет сформулировать следующие выводы.

• 1.    Получен энергетический функционал для решения задачи о собственных колебаниях пластин с низкой трансверсальной жесткостью.

• 2.    Разработана конечно-элементная модель податливой при сдвиге пластины, вектор узловых неизвестных которой включает углы трансверсального сдвига. Сформированы матрица жесткости и матрица инерции для соответствующего элемента пластины.

• 3.    В результате проведенного численного исследования на примере расчета композитной пластины показана актуальность разработанной модели при проведении модального анализа конструкций с низкой трансверсальной сдвиговой жесткостью, а также при учете граничных условий неклассического вида.

Библиографическая ссылка

1. Васильев В. В. Механика конструкций из композиционных материалов. М. : Машиностроение, 1988.

Таблица 2

Значения частот собственных колебаний композитной пластины

Номер моды	Значения собственных частот, Гц
	h = 10 мм		h = 30 мм		h = 50 мм
	Полное защемление	Защемление со свободным сдвигом	Полное защемление	Защемление со свободным сдвигом	Полное защемление	Защемление со свободным сдвигом
1	111,24	110,42	323	306	509	455
2	222,09	220,72	634	608	975	900
3	222,09	220,72	634	608	975	900
4	349,33	347,40	977	943	1 457	1 370
5	380,66	378,74	1 066	1 033	1 592	1 512

VIBRATION OF A PLATE WITH LOW TRANSVERSE SHEAR STIFFNESS

Modal finite element analysis of a plate with low transverse shear stiffness is considered. There are two transverse shear strains at each of four nodes. In modal analysis of a composite plate the urgency of the developed finite element model is shown. Results of numerical research of influence of nonclassic boundary conditions are presented.