Поперечный поток энергии в остром фокусе света с циркулярно-азимутальной поляризацией высокого порядка

Строгое описание электромагнитного поля с линейной поляризацией в остром фокусе было получено в классической работе Ричардса–Вольфа [1]. После этой работы появилось множество других работ, в которых на основе формализма Ричардса–Вольфа [1] изучалось световое поле с более общим состоянием поляризации в фокусе. В [2] изучалась острая фокусировка света с радиальной поляризацией. В [3, 4] рассматривалась спин-орбитальная конверсия при фокусировке света с круговой поляризацией. В [5, 6] исследовалась фокусировка оптического вихря с эллиптической поляризацией. В [7] приведена концепция цилиндрических векторных пучков, которые включают в себя пучки с радиальной и азимутальной поляризацией. В [8– 10] рассмотрена фокусировка света с гибридной поляризацией. Транспонированный вектор Джонса для такой поляризации имеет вид E = (exp (iδ), exp (– iδ)), где δ = αr + β, r – радиальная переменная, α, β – постоянные, E – начальное световое поле. Такая гибридная поляризация на некоторых радиусах линейная, а на других радиусах круговая. Но данная поляризация не зависит от полярного угла φ. Более общий тип гибридной поляризации рассмотрен в [11]. В этой работе рассматривается острая фокусировка с начальным полем, транспонированный вектор Джонса которого уже зависит от полярного угла E = (cosφ cosγ – icos (2ψ – φ) sinγ, sinφ cosγ – isin (2ψ – φ) sinγ), где φ – полярный угол, γ, ψ – постоянные. У такого поля при разном значении полярного угла поляризация либо линейная, либо круговая. Но аналитических выражений для поля и проекций вектора Пойнтинга для такого типа гибрид- ных полей не получено в [11]. В [12] рассмотрена гибридная поляризация вида E = (exp (i5) sinф, cosф), где также φ – полярный угол, а δ – постоянная. Такой тип поляризации является частным случаем (при m = 1) поляризации, рассмотренной в нашей работе. И кроме того, в [12] не приведено аналитических выражений для проекций вектора Пойнтинга. В [13, 14] исследуются пучки с произвольной поляризацией на сфере Пуанкаре. Для таких пучков начальный (до фокусировки) вектор поляризации можно представить в виде E = (exp (–ilφ + iα) cosβ + exp (ilφ + iα) sinβ, iexp (– ilφ + iα) cosβ + iexp (ilφ + iα) sinβ), где l – топологический заряд, φ – полярный угол, (α, β) – углы на сфере Пуанкаре (постоянные). Заметим, что в [13, 14] есть эксперимент по исследованию таких пучков, но нет теории и не получены выражения для поля, интенсивности и проекций вектора Пойнтинга в фокусе. В [15, 16] рассматривается острая фокусировка света с цилиндрической поляризацией высшего порядка, когда начальное поле можно представить в виде E = (cos (pφ + α), sin(pφ + α)), где p – порядок цилиндрической поляризации, α – постоянная. В [17] теоретически исследуются вихревые пучки с произвольным топологическим зарядом m и цилиндрической поляризацией целого порядка n. В этом случае начальное поле имеет вид: E =exp(im φ)(cos (nφ), sin (nφ)).

В данной работе теоретически рассматривается острая фокусировка нового типа гибридной поляризации, отличной от рассмотренных выше. В работе исследуется световое поле с начальной поляризацией вида E =(– i sin ( m φ), cos ( m φ)). В этом случае в начальном поле при изменении полярного угла поляризация меняется от круговой, эллиптической до линейной, и так повторяется m раз за полный оборот полярного угла. В работе получены аналитические выражения для проекций векторов напряженности электрического и магнитного полей в фокусе, а также для распределения интенсивности, проекций вектора Пойнтинга и вектора спинового углового момента.

1. Интенсивность света с гибридной поляризацией в фокусе

Рассмотрим амплитуды начальных векторов напряженности электрического и магнитного полей с гибридной поляризацией m -го порядка в следующем виде:

( - i sin m ф) (- cos m ф )

E = A ( 9 ) 1 4, H = A ( 9 ) 1 ^T I, (1) ^ cos m ф J ^ - i sin m ф )

где E и Н – вектора напряженности электрического и магнитного полей, m – целое положительное число, определяющее порядок цилиндрической поляризации, A(θ) – амплитуда начального светового поля, в зависимости от угла наклона к оптической оси. Поляризация поля (1) называется гибридной, так как она объединяет свойства цилиндрической поляризации m-го порядка и круговой поляризации. На разных азимутальный углах φ поляризация в (1) будет либо круговой (при ф = пn /(4m), n =1,3,5,...), либо эллиптической, либо линейной (при ф = пn/(2m), n = 0,1,2,...). Из (1) также следует, что при m =0 у поля будет однородная линейная поляризация. С помощью формализма Ричардса–Вольфа [1] можно найти проекции вектора напряженности электрического поля в остром фокусе апланатической системы для начального поля вида (1):

m

Ex = — x 2

т • /        , ⁽¹ + i ) T

1 0, m sin( m ф ) +    2    1 2, m + 2

sin ( ( m + 2) ф ) +

+ (-2i) 1 2- m - 2 sin ( ( m - 2) ф )

-im   x , X

E y = — iI 0, m cos( m ф )

-

(1 + i )

I 2, m + 2 ^X

(1 - i )

X cos ( ( m + 2) ф ) + ^-22 1 2, m - 2 cos ( ( m - 2) ф ) ,

E z = i 2 [ (1 + i ) 1 1> m + 1 sin ( ( m + 1) ф ) + + (1 - i ) 1 1, m - 1 sin ( ( m - 1) ф ) ]

и магнитного поля:

i m

H x = у iI 0, m cos( m ф ) +

^12 i ) 1 2, m + 2 cos ( ( m + 2) ф ) -

- (-2i) 1 2, m - 2 cos ( ( m - 2) ф )

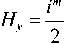
+ (1 - i )

- 1 0, m sin( m ф ) + ^(l + i ) 1 2, m + 2 sin ( ( m + 2) ф ) +

1 2, m - 2 sin ( ( m - 2) ф )

H z = i— [ (1 - i ) 1 1,m + 1 cos ( ( m + 1) ф ) -

-(1 + i) I1, m-1 cos ((m - 1)ф)], где

¹ v , H

5 f 1 0 sin ^{v+ 1}( ⁹ )cos^{3 -v} ( ⁹ ) X , X J ^J₀        2         2

x cos1/2 (9) A (9) eikzcos 9 Jц (x) d 9, где λ – длина волны света, f – фокусное расстояние апланатической системы, x = krsinθ, Jμ (x) – функция Бесселя первого рода и NA = sinθ0 – числовая апертура. Начальная функция амплитуды A(θ) (предположим, что это действительная функция) может быть константой (плоская волна) или в виде Гауссова пучка

A ( 9 ) = exp

Г-у ² sin² 91 ( sin² 9 ₀ ^J

где γ – постоянная. Для проверки уравнений (2) получим из них известные выражения [1, 4] для светового поля с линейной поляризацией:

Ex 0 = —1 2,2 sin ( 2 ф ) ,

E y = - [ 1 0,0 - 1 2,2 cos ( 2 ф ) ] ,                       (6)

E z = 1 1,1 sin ( ф ) .

Отличие в том, что вектор линейной поляризации в (1) направлен вдоль y , а в [1, 4] – вдоль x . Из (2) можно найти распределение интенсивности электрического поля в плоскости фокуса ( z =0):

I m = 4 [ I '² m ⁺ I² m + 2 ⁺ I 22,m " ^{2 - 1} 0, m ( ¹ 2, m + 2 ^{+ 1} 2, m - 2 ) ] ⁺

+ 4 ( I 12 m + 1 + 1 0, m l 2, m + 2 ) sin ( ( m + 1) ф ) +            (7)

+ 4 ( 1 12 m - 1 + 1 0, m l 2, m - 2 ) sin ( ( m — 1) ф ) •

Из (7) при m = 0 следует известное выражение для распределения интенсивности в остром фокусе для начального светового поля с линейной поляризацией [1, 18]:

• 1 0    = 4 ( 1 0 ² ,0 + 2 1 121 + 2 1 22,2 ) - 4 ( 1 121 + 1 0,0 1 2,2 ) cos ( 2 ф ) . (8)

Из (8) видно, что интенсивность имеет два локальных максимума, лежащих на вертикальной оси (при ф = ± п / 2), так как начальная поляризация линейная и направлена вдоль оси y . При m = 1 из (7) следует, что интенсивность в фокусе для гибридного поля (1) первого порядка имеет вид:

• ¹ 1    = “( ¹ 02,1 ^{+ 1} 122 ^{+ 1} 22,1 ^{+ 1} 22,3 ^{+ 1} 0,1 ¹ 2,1 ) ^-

• 41                                                (9)

• - 4 (11,2 + 10,112,3 ) COs (4ф).

2.    Поток энергии в фокусе для света с гибридной поляризацией

Из (9) следует, что распределение интенсивности в фокусе для гибридного поля (1) первого порядка (азимутальная круговая поляризация) имеет 4 локальных максимума (при ф = ±п /4, ± 3 п /4). И в общем случае при произвольном m распределение интенсивности (7) будет иметь 2( m + 1) максимумов, лежащих на лучах, образованных углами ф = ( п + 2 п n )/2 ( m +1), n = 0,1,2,...2 m +1. Моделирование подтверждает эти выводы.

В начальном поле (1) имеется только продольная проекция потока энергии, так как нет продольной составляющей электрического и магнитного полей и нет поперечных компонент вектора Пойнтинга. Но зато есть продольная составляющая спинового углового момента (СУМ). Поэтому из-за эффекта спин-орбитальной конверсии следует ожидать, что в фокусе сформируется поперечный поток энергии. Пока- жем, что это действительно так. Найдем проекции вектора Пойнтинга (потока энергии)

P = Re ( E * x H ) ,

где Re – реальная часть числа, × – знак векторного произведения двух векторов, E * – комплексное сопряжение, в плоскости фокуса ( z =0) для начального поля с гибридной поляризацией (1). Для этого подставим проекции электрического (2) и магнитного (3) полей в (10), получим:

P x = 4 ^[ 1 0, m ( 1 1, m + 1 + 1 1, m - 1 ) cos ф +

+ 1 1, m + 1 1 2, m - 2 cos ( ( m + 1) ф ) cos ( ( m - 2) ф ) +

+ 1 1, m - 1 1 2, m + 2 cos ( ( m - 1) ф ) cos ( ( m + 2) ф ) +

+ 1 1, m + 1 1 2, m + 2 sin ( ( m + 1) ф ) sin ( ( m + 2) ф ) + + 1 1, m - 1 1 2, m - 2 sin ( ( m - 1) ф ) sin ( ( m - 2) ф ) ],

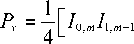
sin ( (2 m + 1) ф ) +

+ 1 0, m l 1, m - 1 sin ( (2 m - 1) ф ) +

+ 1 1, m + 1 1 2, m - 2 cos ( ( m + 1) ф ) sin ( ( m - 2) ф ) -

- 1 1,m - 1 1 2, m + 2 cos ( ( m - 1) ф ) sin ( ( m + 2) ф ) +

+ 1 1, m + 1 1 2, m + 2 sin ( ( m + 1) ф ) cos ( ( m + 2) ф ) -

- 11,m-112,m-2 sin ((m - 1)ф) cos ((m - 2)ф)], p =11 /,2 -4/,2 . Pz 4 I 1 0,m 2 1 2,m+2

-

2 I 2, m - 2

Хотя выражения для проекций вектора Пойнтинга (11) громоздкие, некоторые общие выводы можно сделать. Из (11) следует, что продольный поток энергии при любом m имеет радиальную симметрию (не зависит от угла φ). На оптической оси продольный поток энергии будет положительный и отличен от нуля только при m =0 (линейная поляризация): P z ( r = z = 0) = 1 ₀ ² ,₀ / 4 . Также на оптической оси в фокусе продольная проекция вектора Пойнтинга из (11) будет отличной от нуля и отрицательной только при m = -2 или m = 2: P z ( r = z = 0) = - 1 ₂ ² ,₀ /4 . То есть на оптической оси в фокусе для гибридной поляризации также имеет место обратный поток энергии при m = ± 2, как и для обычной азимутальной поляризации второго порядка [18, 19]. Из (11) при φ =0 можно получить выражение:

P x ^{( ф} = ⁰⁾ = 4 [ ¹ 0, m ( ¹ 1, m + 1 ^{+ 1} 1, m - 1 ) ^{+ 1} 1, m + 1 ¹ 2, m - 2 ⁺

^{+ 1} 1, m - 1 ¹ 2, m + 2 ] >  ⁰.

Из (11) также можно получить, что Py (y =0)=0, Px(ф = 0)=-Px(ф = п)>0. То есть при любом m на горизонтальной оси поперечный поток энергии всегда направлен вдоль этой оси, и в разные стороны от центра. Также из (11) следует, что поперечный поток энер- гии на вертикальной оси y направлен вдоль этой оси, так как Px (ф = п /2) = Px (ф = 3п /4) = 0. Из (11) также следует, что поток вдоль оси y меняет знак при переходе через центр: Py(ф=п/2)=-Py(ф = 3п/4)^ 0. Знак поперечного потока вдоль оси y будет чередоваться. Если, например, при m = 1 поток энергии вдоль оси y направлен к центру, то при m =2 он будет направлен от центра. Итак, при m = 1 поперечный поток энергии на горизонтальной оси направлен от центра, а на вертикальной оси к центру. Это возможно, если в первом и третьем квадрантах поперечный поток энергии вращается против часовой стрелки, а во втором и четвертом квадрантах – по часовой. Далее, при m =2 поперечный поток энергии на вертикальной оси y сменит направление и будет направлен от центра, и поток по горизонтальной оси x будет по-прежнему направлен от центра. Это возможно, если в четырех квадрантах будут четыре линии (под углом 45 градусов), на которых поток энергии будет направлен к центру. То есть при m =2 сформируются 8 вихревых поперечных потоков энергии (по 2 в каждом квадранте), в которых направление вращения энергии будет чередоваться (по часовой и против часовой стрелки). Эти рассуждения можно продолжить и можно показать, что при произвольном m в фокусе сформируются 4m вихревых потоков энергии. Причем направление вращения меняется на противоположенное при переходе от вихря к вихрю.

Рассмотрим для простоты частные случаи выражения (11). Из (11) также следует, что при m =0 (линейная поляризация) в фокусе поперечные составляющие потока энергии равны нулю: P x = P y =0. Это можно проверить непосредственной подстановкой m =0 в (11), и с учетом свойств интегралов (4): I p , – q = (–1) ^qI p, + q . При m >0 поперечный поток энергии (11) отличен от нуля. Напомним, что для цилиндрической поляризации m -го порядка поперечный поток энергии в фокусе всегда равен нулю [18]. При m = 1 (круговая азимутальная поляризация) из (11) следуют выражения для проекций потока энергии:

P x = 4 [ I °-‘ ( I ‘-2 ⁺ 1 ‘-° ) cos Ф ⁺ 1 ‘-2 1 2-3 sin 2 ф sin 3 ф + + I 1-° I 2-3 cos3 ф- I 1-2 1 2-1 cos2 ф COS ф ] ,

P y = 4 ^[ I °-1 ( 1 1-2 sin 3 ф — I ‘-° sin ф ) +

+ 1 1-2 1 2-3 cos 2 ф cos3 ф - I 1-° I 2-3 sin3 ф +

+ I 1-2 1 2-1 cos2 ф sin ф ] -

• ¹ 1 /2                         I

P z = 4 I I °-1    2 I 2-3 2 I 2-1 I .

Из (13) видно, что продольная составляющая потока энергии имеет вид кольца с нулем на оптической оси. И поперечные составляющие потока энергии отличны от нуля и не имеют радиальной симметрии.

Поперечные составляющие вектора Пойнтинга в фокусе, как видно из (13), имеют следующую структуру:

ф = °:   Px = a + в > °- Py = °- ф = п/2: Px = °-Py =-A + B < °- ф = п : Px =-(A + B) < °- Py, = °-             (14)

ф = 3 п /2: P x = °- P y = A - B >  °-

A = I °-1 ( 1 1-2 + 1 1-° ) ^/4- B = 1 1-° I 2-3 ^— 1 1-2 I 2-1 .

Из (14) видно, что на горизонтальной оси в плоскости фокуса поперечный поток энергии направлен вдоль горизонтальной оси от центра, а на вертикальной оси поперечный поток энергии направлен вдоль вертикальной оси к центру. Это может быть, если поперечный поток энергии вращается в первом и третьем квадрантах против часовой стрелки, а во втором и четвертом квадрантах – по часовой стрелке.

Из (11) можно сделать еще один общий вывод, не прибегая к моделированию. В выражении для проекции вектора Пойнтинга в (11) P y функция синуса с максимальной пространственной частотой колебаний есть sin (2 m + 1) ф . Это означает- что при заданном r интегралы из (4), входящие в (11), будут постоянными величинами, а все выражение P y будет зависеть только от угла φ, и при обходе вокруг центра в плоскости фокуса по окружности радиуса r величина P y сменит знак 2(2 m + 1) раз.

3.    Спиновый угловой момент в фокусе поля с гибридной поляризацией

Напомним, что продольная проекция вектора плотности спина или спинового углового момента (СУМ) для цилиндрической поляризации любого порядка равна нулю [18]. Покажем, что для гибридной поляризации (1) в фокусе продольная проекция СУМ будет отлична от нуля. Действительно, воспользуемся выражением для СУМ в виде [4]:

S = Im ( E * x E ) -                                 (15)

где Im – мнимая часть числа. Подставим проекции электрического поля из (2) в (15), получим для продольной проекции СУМ:

S z = ^{1 [} I °- m ( 1 2- m + 2 - 1 2- m - 2 ) sin 2 ф +

4 ^L                                            (16)

+ ( I Im - 1 2- m - 2 1 2,m + 2 ) sin ( 2 m ф ) ] •

Из (16) при m =0 (линейная поляризация) следует, что S z =0. А при m = 1 вместо (16) получим:

S z = 4 [ I °-1 ( 1 2-3 + 1 2-1 ) + ( 1 21 + 1 2-1 1 2-3 ) ] Sin2 ф .     (17)

Из (16) следует, что число смены знака осевой проекции вектора СУМ в плоскости фокуса будет равно 4m, так как в (16) входит функция sin(2mφ). Получается, что в фокусе сформируются 4m локаль- ных вихрей поперечного потока энергии и 4m локальных областей с положительной или отрицательной продольной проекцией вектора СУМ. Причем в тех областях, где поперечный поток энергии вращается против часовой стрелки и вектор поляризации будет вращаться против часовой стрелки, а значит, проекция вектора СУМ будет положительной (Sz >0). И наоборот, в тех локальных областях плоскости фокуса, в которых поперечный поток энергии вращается по часовой стрелке и вектор поляризации будет вращаться по часовой стрелке, а значит, продольная проекция вектора СУМ будет отрицательная (Sz <0). Если в плоскости фокуса расположить диэлектрические микрочастицы, размер которых немного меньше локальной области вращения потока энергии, то они будут вращаться вокруг своей оси. Причем соседние частицы будут вращаться в разные стороны.

4.    Результаты моделирования фокусировки света с гибридной поляризацией

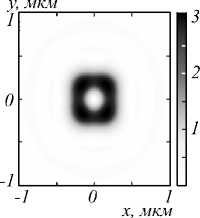
Расчеты производились с помощью формализма Ричардса–Вольфа [1]. Моделировалась фокусировка плоской волны с гибридной поляризацией (1) в воздухе n = 1. Длина волны – 532 нм. Апланатический объектив с числовой апертурой NA=0,95. Множители перед интегралами (4) в формулах Ричардса– Вольфа считались единичными. На рис. 1 показаны распределения интенсивности (а) и компонент вектора Пойнтинга Px (б) Py (в) и Pz (г) в плоскости фокуса при фокусировке плоской волны с гибридной поляризацией (1) при m = 1. Из рис. 1 видно, что интенсивность имеет 2(m + 1)=2(1 + 1)=4 локальных макси- мума, расположенных в углах контура квадрата. В центре фокуса имеет место ноль интенсивности. На рис. 1б, в показаны распределения поперечного потока энергии или поперечные проекции вектора Пойн-тинга Px (б) Py (в). Из рис. 1б, в видно, что поток энергии меняет знак при обходе по замкнутому контуру вокруг центра 2(2m + 1)=6 раз. На рис. 1г показана продольная проекция вектора Пойнтинга Pz, которая имеет вид кольца с нулевым значением в центре. Распределения на рис. 1 подтверждают выводы, сделанные из полученных выражений для интенсивности (9) и потока энергии (11).

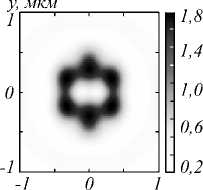
На рис. 2 показаны распределения интенсивности (а) и компонент вектора Пойнтинга P x ( б ) P y ( в ) и P z ( г ) в плоскости фокуса при фокусировке плоской волны с гибридной поляризацией (1) при m =2. Вид картин на рис. 2 также подтверждает выводы теории, следующие из выражений (9) и (11). Действительно, на рис. 2 а у распределения интенсивности видны 2( m + 1)=6 локальных максимумов, лежащих на замкнутой кривой вокруг центра. На рис. 2 б, в показаны распределения поперечного потока энергии или поперечные проекции вектора Пойнтинга P x ( б ) P y ( в ). Из рис. 2 б, в видно, что поток энергии меняет знак при обходе по замкнутому контуру вокруг центра 2(2 m + 1)= 10 раз. На рис. 2 г показана продольная проекция вектора Пойнтинга P z , которая имеет вид кольца. Величина потока энергии в центре отрицательная и равна P z ( r = z = 0) = - 1 20 / 4 , как следует из (11). Из рис. 1 и 2 видно, что максимум продольного потока энергии примерно в два раза превышает максимум поперечных потоков энергии.

а)

б)

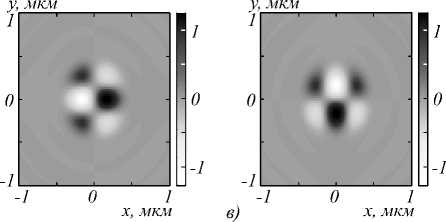
Рис. 1. Распределения интенсивности (негатив) (а) и компонент вектора Пойнтинга P x (б) P y (в) и P z (г) в плоскости фокуса при фокусировке плоской волны с гибридной поляризацией (1) при m = 1

X, Л1КЛ1

в)

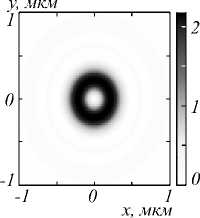
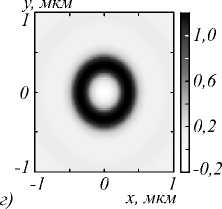
Рис. 2. Распределения интенсивности (негатив) (а) и компонент вектора Пойнтинга P x (б) P y (в) и P z (г) в плоскости фокуса при фокусировке плоской волны с гибридной поляризацией (1) при m = 2

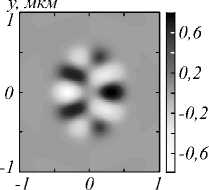
На рис. 3 показаны распределения компонент спинового углового момента Sx (а) Sy (б) и Sz (в) при фокусировке плоской волны с гибридной поляризацией (1) при m = 1. Из рис. 3в видно, что число смен знака продольной проекции вектора СУМ равно 4m =4. Для продольной проекции СУМ это следует из выражения (17).

На рис. 4 показаны распределения компонент спинового углового момента Sx (а) Sy (б) и Sz (в) при фокусировке плоской волны с гибридной поляризацией (1) при m = 2. Из рис. 4в видно, что число смен знака продольной проекции СУМ равно 4m = 8. Для продольной проекции СУМ это следует из выражения (17).

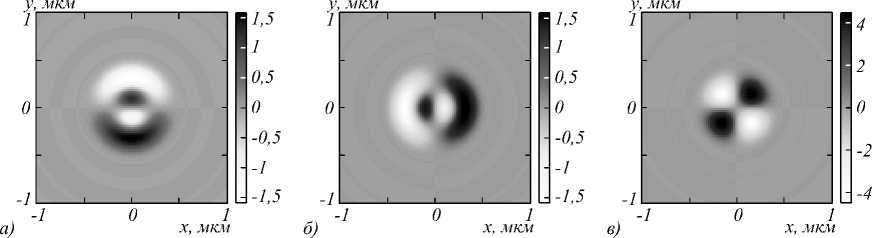
Рис. 3. Распределение компонент спинового углового момента S x (а), S y (б) и S z (в) при фокусировке плоской волны

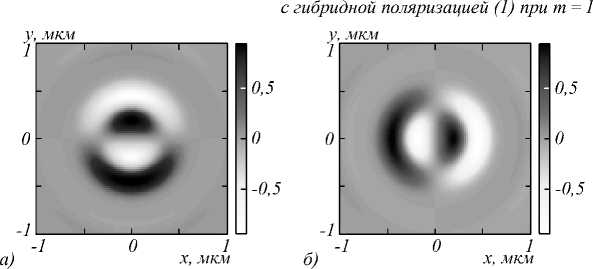
Рис. 4. Распределение компонент спинового углового момента S x (а), S y (б) и S z (в) при фокусировке плоской волны с гибридной поляризацией (1) при m = 2

На рис. 5 показаны распределения интенсивности и стрелками показано направление поперечного вектора Пойнтинга в фокальной плоскости при фокусировке плоской волны с гибридной поляризацией (1) с m =2 (а) и m =3 (б). Из рис. 5 видно, что число вихрей поперечного потока равно 4m = 8 (а) и 4m = 12 (б). Это следует из выражений для поперечных проекций вектора Пойнтинга (11). Из рис. 5 также можно видеть, что центры вихрей поперечного потока энергии в фокусе не совпадают с локальными максимумами интенсивности. Центры вихрей находятся в точках, в которых поперечный поток энергии равен нулю. Из сравнения рис. 4в и рис. 5а видно, что число областей с положительным и отрицательным значением продольной проекции СУМ (4m =8) совпадает с числом вихрей поперечного потока энергии (4m = 8).

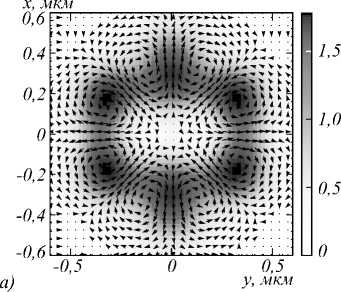
Рис. 5. Распределение интенсивности (полутона) и величина и направление вектора Пойнтинга (стрелки) в фокальной плоскости при фокусировке плоской волны с гибридной поляризацией (1) с m = 2 (а) и m = 3 (б)

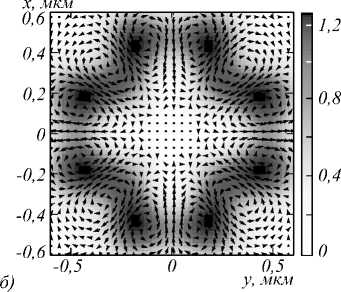
Из сравнения рис. 4в и рис. 5а также видно, что в тех областях плоскости фокуса, где поперечный поток вращается против часовой стрелки, продольная проекция СУМ положительная (Sz >0). А в тех областях плоскости фокуса, где поперечный поток энергии вращается по часовой стрелке, продольная проекция СУМ отрицательная (Sz <0). То есть вектор поляризации в плоскости фокуса вращается против часовой стрелки в тех областях, где и поперечный поток энергии вращается против часовой стрелки. И наоборот, вектор поляризации в плоскости фокуса вращается по часовой стрелке в тех областях, где и поперечный поток энергии вращается по часовой стрелке. Это согласуется с эффектом спин-орбитальной конверсии.

Заключение

В данной работе рассмотрена фокусировка света с неоднородной гибридной поляризацией, объединяющей свойства цилиндрической поляризации m -го порядка и круговой поляризации – циркулярноазимутальной поляризацией m -го порядка. С помощью формализма Ричардса–Вольфа рассмотрена острая фокусировка света такой поляризации, получены аналитические выражения в фокусе для проекций векторов напряженности электрического и магнитного полей, распределения интенсивности, проекций вектора Пойнтинга и спинового углового момента. Теоретически и численно показано, что интенсивность в фокусе гибридных пучков имеет 2( m + 1) локальных максимумов, расположенных вдоль окружности с нулевой интенсивностью на оптической оси. Показано, что в фокусе имеется 4 m вихрей поперечного потока энергии, центры которых расположены между локальными максимумами интенсивности. Также показано, что поперечный поток энергии меняет направление вращения 2(2 m + 1) раза при обходе в плоскости фокуса вокруг оптической оси. При этом продольная проекция спинового углового момента в фокусе меняет знак 4 m раза. В тех областях плоскости фокуса, где поперечный поток энергии вращается против часовой стрелки, продольная проекция спинового углового момента положительная, а вектор поляризации вращается в плоскости фокуса против часовой стрелки. И наоборот, где поток энергии вращается по часовой стрелке, там и вектор поляризации вращается по часовой стрелке, а продольная проекция спинового углового момента отрицательная.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение» и «Заключение», Российского научного фонда (грант № 18-19-00595) в части «Результаты моделирования фокусировки света с гибридной поляризацией», Российского фонда фундаментальных исследований РФФИ (грант № 18-29-20003) в части «Интенсивность света с гибридной поляризацией в фокусе»).