Поперечный спиновый эффект Холла и поляризационная твист-лента в остром фокусе
Автор: Котляр В.В., Ковалев А.А., Телегин А.М., Козлова Е.С.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 6 т.48, 2024 года.
Бесплатный доступ
В данной работе мы с помощью формализма Ричардса–Вольфа нашли явные аналитические выражения для координат большой и малой осей эллипса поляризации с центром в плоскости фокуса для цилиндрического векторного пучка целого порядка n. У такого пучка большая ось эллипса поляризации лежит в плоскости фокуса, а малая ось – перпендикулярна плоскости фокуса. Поэтому эллипс поляризации перпендикулярен плоскости фокуса, и вектор поляризации вращается по часовой или против часовой стрелки в этой плоскости (оптические колеса). И так как волновой вектор тоже перпендикулярен плоскости фокуса, то получается, что эллипс поляризации и волновой вектор лежат в одной плоскости, и в некоторый момент времени вектор поляризации может совпадать с волновым вектором, что является необычным для поперечных электромагнитных колебаний. Для цилиндрического векторного пучка вектор спинового углового момента лежит в плоскости фокуса. И при обходе по некоторой окружности с центром на оптической оси вектор спина на некоторых участках окружности направлен против часовой стрелки, а на других участках – по часовой стрелке. Этот эффект можно назвать поперечным (азимутальным) спиновым эффектом Холла, в отличие от известного продольного спинового эффекта Холла в остром фокусе. Под продольным спиновым эффектом Холла понимают разделение в плоскости фокуса областей с разным знаком продольной проекции вектора спинового углового момента. В работе показано, что таких областей всегда четное число и что при обходе по окружности вектор большой оси эллипса поляризации формирует двухстороннюю твист-поверхность с четным числом поворотов.
Спиновый угловой момент, формулы Ричардса–Вольфа, спиновый эффект Холла, оптический вихрь, цилиндрический векторный пучок, плоская волна, поляризационная твист-лента
Короткий адрес: https://sciup.org/140310408
IDR: 140310408 | DOI: 10.18287/2412-6179-CO-1504
Текст научной статьи Поперечный спиновый эффект Холла и поляризационная твист-лента в остром фокусе
В [1] экспериментально наблюдали поляризационную ленту Мебиуса в остром фокусе векторного лазерного пучка, сформированного q-пластиной. В [1] показано, что в фокусе начального оптического вихря с топологическим зарядом n = 1 поляризационная лента Мебиуса делает 3 полуоборота, а для n =3 делает пять полуоборотов. В [2] c помощью моделирования показали, как можно сформировать экзотические поляризационные ленты Мебиуса в фокусе. В [3] изучаются поляризационные ленты Мебиуса в наклонных параксиальных векторных пучках. Кроме односторонних поляризационных лент Мебиуса, у параксиальных и непараксиальных векторных пучков имеются и двухсторонние твист-полоски с четным числом полуоборотов [4–7].
С другой стороны, в работах, посвященных спиновому эффекту Холла в фокусе [8– 10], показано, что при увеличении топологического заряда векторных вихревых пучков увеличивается число областей в фокусе, в которых спин меняет знак. Эти области со спином разного знака появляются парами, чтобы общий спин пучка оставался равен нулю. То есть число областей разного спина, лежащих вдоль некоторой окружности с центром на оптической оси, всегда четное. Поэтому эллипс поляризации при обходе в плоскости фокуса по такой окружности будет делать четное число полуоборотов, то есть целое число полных оборотов. А поверхность, которую будет формировать вектор большой (или малой) оси эллипса поляризации, не будет односторонней лентой Мебиуса, как в [1, 2], а будет двухсторонней поверхностью с четным числом полуоборотов [4]. Такие поляризационные ленты в [4] названы твист-поверхностями (twisted ribbons).
Чтобы определить расположение эллипсов поляризации в плоскости фокуса, нужно использовать уравнения для координат большой и малой осей эллипса поляризации, полученные М. Берри [11]. Под координатой оси эллипса поляризации понимается координата одного из концов большой или малой оси эллипса, если начало координат помещено в центр эллипса.
Обычно большую и малую оси эллипса поляризации рассчитывают численно. В данной работе мы нашли два примера векторных полей (цилиндрическое векторное поле n -го порядка и оптический вихрь с топологическим зарядом n и азимутальной поляризацией), для которых получены аналитические выражения для распределения координат большой и малой осей эллипса поляризации в плоскости острого фокуса, используя формализм Ричардса–Вольфа [12].
1. Проекции светового поля, интенсивность и проекции спинового углового момента в фокусе
Рассмотрим начальное световое поле, вектор Джонса которого имеет вид:
f l ^
Е ( ф ) = exp( in ф ) 1 0 1 , (1)
где ( r , φ) – полярные координаты в сечении пучка, n – топологический заряд, целое число, вектор линейной поляризации направлен по горизонтальной оси x . В [13] получены проекции электрического и магнитного векторов в плоскости острого фокуса для начального поля (1):
in -i
E x = — e in ф ( 2 1 o, n + e2i ф 1 2, n +2 + e - 2i ф I 2,n -2 ) ,
E y = i ^-en ’ ( e - 2i ф 1 2, n -2 - e2 ф 1 2, n +2 ) , (2)
E z = inein ф ( e 1 1, n -1 - e^ 1 1, „ + i ) .
В (2) входят функции I μ ν , зависящие только от радиальной переменной r :
a f0^
L = 2 kf [sin v+1 — cos 3 v — cos — x
J o 1 2 J 1 2 ) 1 2 ) (3)
xA (0)eikcos0 Jц (kr sin 0) d0, где k = 2π/λ – волновое число монохроматического света с длиной волны λ, f – фокусное расстояние фокусирующей линзы, α – максимальный угол наклона лучей к оптической оси, определяющий числовую апертуру апланатической линзы NA = sin α, Jμ(ξ) – функция Бесселя первого рода μ-го порядка. Функция A(θ) – действительная функция, определяющая радиально-симметричную амплитуду начального поля, зависящую от угла наклона θ луча, исходящего из точки на начальном сферическом фронте и сходящегося в центр плоскости фокуса.
Далее найдем с помощью (2) все три проекции вектора спинового углового момента (СУМ) [14]:
S = 8b Im ( E * x E ) • (4)
где ω – угловая частота света. Постоянную 1/(8πω) будем опускать.
Подставляя (2) в (4), получим выражения для проекций вектора плотности спина или СУМ в фокусе для начального поля (1):
S x = M ( r )sin ф + N ( r )sin3 ф ,
S y = O ( r )cos ф + M ( r )cos ф + N ( r )cos3 ф ,
Sz 2
!, n -2
- 1 2, n +2 ) ( 1 2, n -2 + 1 2, n +2 + 2 1 0, n COs2 ф ) ,
M ( r ) = 1 1, n -1 1 2, n -2 - 1 1, n +1 1 2, n +2 ,
N ( r ) = 1 1, n -1 1 2, n +2 1 1, n +1 1 2, n -2 ,
O ( r ) = 2 1 0, n ( 1 1, n -1 - 1 1, n +1 ) .
Аналогично можно найти полную интенсивность в фокусе I = I x + I y + I z = | E x |2 + | E y |2 + | E z |2 и отдельные ее составляющие:
I x = 1 02,,
4 1 22, n -2 + 4 1 22, n +2 + cos2 фx
x( I 0, n I 2, n-2 + I 0, n I 2, n +2 ) + 4 I 2, n -2 I 2, n +2 cos 4 ф ,
I y = 4 I 22, n -2 + 4 I 22, n +2 4 I 2, n -2 I 2, n +2 cos 4 ф ,
I z = 1 12 n -1 + 12 n +1 - 2 1 1, n -1 1 1,n +1 cos 2 ф ,
I = I <2
1 I 2
2 I 2, n - 2
+ 2 I 2, n +2
+ I 1, n -1
+ 1 12 n +1 +
+ cos2 ф( I 0, n I 2, n-2 + I 0, n I 2, n +2 - 2 1 1, n -1 1 1, n +1
2. Представление вектора напряженности поля через вектора осей эллипса поляризации
В [11] приведены формулы для расчета индекса поляризационных сингулярностей произвольных векторных полей. Следуя этой работе, запишем, что вектор электрического поля E можно представить через действительные вектора A и B , которые вытянуты вдоль большой и малой осей эллипса поляризации с центром в данной точке пространства:
E = e i ( A + i B ), I = |A| 2 + |B| 2 ,
A - B = 0, |A| > Bl,
Y = 2 arg ( E - E ) ,
A = -^Re( E^E ’ - E * ).
VEE ' ’
B = -^Im ( eVE^E 7 ), VE-E V ’
S = Im ( E * x E ) = 2( A x B ).
В уравнении (7) точкой обозначено скалярное произведение векторов, крестом × обозначено век-
торное произведение, Re и Im – вещественные и мнимые части числа, S – с одной стороны, вектор СУМ, а с другой стороны, вектор нормали к плоскости поляризационного эллипса, образованного вектора A и B , I – интенсивность, выраженная через проекции векторов осей поляризационного эллипса.
Заметим, что представление комплексного поля E через действительные вектора A и B не однозначно. То есть не для любого разложения вектора A и B будут ортогональны, но для любого разложения они будут лежать в плоскости, перпендикулярной вектору СУМ, то есть в плоскости поляризационного эллипса. Представление (7) также применимо к световому полю в фокусе (2) и позволяет найти явные выражения для двух векторов A и B в фокусе поля (1). Действительно, вектор напряженности электрического поля (2) можно представить в виде, аналогичном представлению (7), просто выделив реальную и мнимую части:
E = ei ( A + i B ),
A x = 1 0, n + P ( r ) cos 2 ф ,
A y = P ( r ) sin 2 ф ,
A z = F ( r )sin ф ,
B x = Q ( r )sin2 ф ,
B y =- Q ( r )cos2 ф , (8)
B z = L ( r )cos ф ,
P ( r ) = ( 1 2, n -2 + 1 2, n +2 ) / 2, F ( r ) = 1 1, n -1 + 1 1, n +1 ,
Q ( r ) = ( 1 2, n +2 — 1 2, n -2 ) / 2, L ( r ) = 1 1, n -1 — 1 1, n +1 ,
Г пЛ ПY = n Ф + т -?.
Конечно, нет гарантии, что вектора A и B в (8) образуют две оси эллипса поляризации в точке ( x, y, z =0), но можно убедиться, что полученные проекции векторов (8) позволяют получить проекции СУМ (5) и составляющие интенсивности (6), так как:
S = Im ( E * X E ) = 2( A x B ), I =lAl 2 + Bl2 .
Вектор СУМ (9) перпендикулярен векторам A и B, а его модуль равен произведению модулей векторов A и B , умноженному на синус угла η между ними, величина которого не обязана быть равной π /2:
|S| = |A||B| sin n .
Из (10) следует, что линейная поляризация в фокусе поля (1) соответствует нулю модуля либо вектора A , либо вектора B : | S | = | A | = | B | =0. Из (8) следует, что для любого топологического заряда n найдется такой радиус окружности r 0 в плоскости фокуса с центром на оптической оси ( r =0), что будет выполняться равенство
2 Q ( r 0 ) = I 2, n +2 I 2, n -2 = °.
На этой окружности в плоскости фокуса вектор B поляризационного эллипса будет иметь только продольную проекцию:
B x = Q ( r o )sin2 ф = °, B y =- Q ( r o )cos2 ф = °, B z = L ( r ° )cos ф .
И так как вектор СУМ (9) перпендикулярен вектору B , то продольная проекция вектора СУМ будет равна нулю, а сам вектор СУМ S будет лежать в плоскости фокуса. Вектор B будет иметь нулевую длину в двух точках на окружности радиуса r 0 , а именно при φ = π /2 и φ =3π /2, так как в этих точках B z =0. Рассмотрим подробнее, как изменяется вектор СУМ в окрестностях этих точек. Например, при угле немного меньше, чем φ = π /2, продольная проекция вектора B в (12) будет положительная ( L ( r 0 ) cosφ >0), если L ( r 0 ) >0, а при угле немного больше, чем φ = π /2, продольная проекция вектора B в (12) будет отрицательная ( L ( r 0 ) cosφ <0). А вектор A , не лежащий в плоскости фокуса в точках на окружности радиуса r 0 и почти не меняющий своего направления до и после угла φ = π /2, направлен преимущественно вдоль оси x , так как:
A x = 1 0, n ( r ° ) + P ( r ° ) cos 2 ф ® I °, n ( r ° ) > 0,
A y = P ( r ° )sin2 ф» °,
A z = F ( r ° )sin ф» F ( r ° ),
I °, n ( r ° ) >> P ( r ° ), I °, n ( r ° ) >> F ( r ° ).
Неравенства в (13) следуют из работы [8]. Тогда вектор СУМ, меняясь вдоль окружности радиуса r 0 , при угле немного меньше φ = π /2 будет направлен почти против вертикальной оси y , а при угле немного больше φ = π /2 вектор СУМ будет направлен почти вдоль вертикальной оси y . То есть вектор СУМ, лежащий в плоскости фокуса при обходе по окружности радиуса r 0 при прохождении точки с углом φ = π /2 поменяет свое направление на противоположенное. В самой точке на окружности с углом φ = π /2 вектор СУМ будет равен нулю. Смену направления вектора СУМ, лежащего в плоскости фокуса, при переходе точки c линейной поляризацией ( B =0) можно назвать поперечным спиновым эффектом Холла. Его следует отличать от продольного спинового эффекта Холла [8, 9].
В (5) продольная проекция СУМ зависит от cos(2φ), и поэтому при обходе по некоторой окружности будет менять знак 4 раза. То есть в плоскости фокуса имеются 4 области, в двух из которых продольная проекция СУМ положительная, а в двух других отрицательная. Разделение областей в плоскости фокуса с продольным СУМ разного знака можно назвать продольным спиновым эффектом Холла [8,
-
9] . То есть в данном параграфе мы показали, что у начального светового поля (1) на некоторых окружностях в плоскости фокуса с центром на оптической оси вектор СУМ лежит в плоскости фокуса и может четное число раз менять свое направление на противоположенное. Мы назвали этот эффект поперечным спиновым эффектом Холла.
-
3. Поляризационная твист-лента в плоскости фокуса
Теперь для начального поля (1) в плоскости фокуса выберем окружность другого радиуса r 1 , на котором продольная проекция B z равна нулю:
L ( r i ) = 1 1, n -i - 1 1, n +i = 0. (14)
При этом вектор B будет лежать в плоскости фокуса, а вектор А по-прежнему почти будет лежать в плоскости фокуса и будет вытянут вдоль горизонтальной оси (13). Из (5) видно, что при 0< φ < π /4 продольная проекция СУМ будет положительная S z =0,5( 1 2, n -2 — 1 2, n +2 )( 1 2, n -2 + 1 2, n +2 + 2 1 0, n COS 2 ф ) > 0, еСЛИ I 2, n –2 – I 2, n +2 >0 на окружности радиуса r 1 , а при угле φ = π/2 продольная проекция СУМ будет отрицательная, так как 2 I 0, n > I 2, n –2 + I 2, n +2 . Значит, при некотором угле φ из диапазона π/4< φ < π/2 продольная проекция СУМ будет равна нулю:
S z = 0, 1 2, n -2 + 1 2, n +2 = 2 1 0,n COs2 ф . (15)
Из (5) следует, что при условии (14) на окружности радиуса r 1 поперечные проекции СУМ будут иметь более простой вид:
S x = 2 M ( r 1 )sin ф cos2 ф , S y =- 2 M ( r 1 )cos ф sin2 ф .
Смена знака продольной проекции СУМ в плоскости фокуса поля (1) означает наличие в фокусе продольного спинового эффекта Холла. При обходе по окружности радиуса r 1 продольная проекция СУМ будет менять знак 4 раза при любом номере n . Получается, что поверхности эллипсов поляризации, центры которых лежат на окружности радиуса r 1 в плоскости фокуса, при малых углах φ почти лежат в плоскости фокуса и «смотрят» вдоль оптической оси. При угле, в котором S z =0 (15), поверхности эллипсов поляризации повернуты перпендикулярно к плоскости фокуса. И при угле немного больше этого угла (15) поверхности эллипсов поляризации повернуты в обратную сторону и «смотрят» против оптической оси. Получается, что при обходе по окружности с центром на оптической оси, лежащей в плоскости фокуса поверхность, составленная из эллипсов поляризации, 2 раза «смотрит» вдоль оптической оси (пусть вектор большой оси эллипса направлен почти вдоль оси x ) и 2 раза «смотрит» против оптической оси (тогда вектор большой оси эллипса направлен почти против оси x ). В точках
«переворота» (таких точек на окружности 4), определяемых условием (15), плоскость поляризации «смотрит» перпендикулярно оптической оси. Таким образом мы показали, что продольный спиновый эффект Холла сопровождает наличие в фокусе поляризационной двухсторонней твист-ленты (twisted ribbons [4]), в отличие от односторонней поляризационной ленты Мебиуса [1, 2]. И число разворотов этой твист-ленты совпадает с числом областей с продольным спином разного знака. Численное моделирование подтвердит эти рассуждения.
-
4. Поляризационная твист-лента в плоскости фокуса
-
4.1. Цилиндрические векторные поля
-
Рассмотрим вектор Джонса в начальной плоскости векторного цилиндрического пучка n -го порядка ( n – целое число):
( cos n ф'!
Е ( Ф ) = 1 . | . (17)
^Sin nф J
Выражения для проекций вектора напряженности электрического поля в плоскости фокуса для начального поля (17) известны [8, 12]:
E x = i n - 1 ( 1 0, n cos n ф + 1 2, n - 2 cos( n — 2) ф ) ,
E y = i n - 1 ( 1 0, n sin n ф- 1 2, n -2 sin( n - 2) ф ) , (18)
E z = 2 i n 1 1, n -1 cos( n - 1) ф .
В (18) интегралы I μ ν определены в (3). Представим проекции поля (18) через проекции векторов A и B , согласно (8) получим:
E = e i ( A + i B ),
A x = 1 0, n cos n ф + 1 2, n -2 cos( n - 2) ф ,
A y = 1 0, n sin n ф - 1 2, n - 2 sin( n - 2) ф ,
A z = 0,
B x = 0, (19)
B y = 0,
B z = 2 1 1, n -1 Cos( n - 1) ф ,
Y = ( n - 1) 2
Из (19) видно, что вектора A и B, лежащие в плоскости эллипса поляризации, ортогональны друг к другу: AB =0. И так как I 0 ,n >I 1 ,n- 1 , то вектор A является вектором большей оси эллипса поляризации, а вектор B – вектор меньшей оси эллипса поляризации. Так как вектор B имеет только продольную координату, то он перпендикулярен плоскости фокуса. А вектор A имеет только поперечные проекции, и, значит, он лежит в плоскости фокуса. А вектор плотности спина S , перпендикулярный этим двум векторам, также лежит в плоскости фокуса и имеет такие проекции:
S x = 4 1 1, n -i cos ( ( n - 1 ) ф ) х
x[ 1 0,n sin( n ф ) - 1 2, n -2 sin ( ( n - 2) ф ) ] ,
S y =- 4 1 1, n -i cos ( ( n - 1 ) ф ) х (20)
x[ 1 0, n cos( n ф ) + 1 2, n -2 cos ( ( n - 2) ф ) ] ,
S z = 0.
То есть в данном случае ситуация, которая для поля (1) имела место только на окружности радиуса r 0 , для поля (17) имеет место во всей плоскости фокуса. Причем линейная поляризация в фокусе будет тогда, когда cos( n –1) φ =0, то есть при углах φ p = π (1/2 + p ) /( n –1), где p = 0,1,2,… . Причем при углах немного меньших, чем угол φ p , проекция вектора B положительная, если I 1 ,n– 1 >0, а при углах, немного больших, чем угол φ p , проекция вектора B отрицательная. При этом вектор А , который лежит в плоскости фокуса, почти не изменяется. Получается, что вектор плотности спина S , который также лежит в плоскости фокуса, при переходе через углы φ p меняет направление на противоположенное. Таким образом, для поля (17) нет в плоскости фокуса продольного спинового эффекта Холла, но есть поперечный спиновый эффект Холла. То есть на окружности любого радиуса в плоскости фокуса с центром на оптической оси будут лежать 4( n –1) областей, в которых при переходе между соседними областями поперечный спин S ± будет менять направление на противоположенное. При этом на этой окружности будут лежать 4( n –1) точек, в которых поляризация линейная (вектор B равен нулю) и поперечный спин также равен нулю, S ± = 0. То есть при обходе по любой окружности с центром на оптической оси и лежащей в плоскости фокуса, эллипс поляризации будет всегда перпендикулярен плоскости фокуса, а вектора поляризации будут вращаться в плоскости эллипса, как спицы в колесе. То есть световое поле (17) демонстрирует в остром фокусе эффект «оптических колес» [15]. Интересно, что свет, пересекая плоскость фокуса, не является светом с поперечной поляризацией, так как волновой вектор и эллипс поляризации лежат в одной плоскости.
-
4.2. Оптический вихрь с азимутальной поляризацией
Рассмотрим еще один пример начального векторного светового поля, у которого можно аналитически найти в плоскости фокуса проекции векторов большой и малой осей эллипса поляризации. Вектор Джонса начального оптического вихря с топологическим зарядом n и азимутальной поляризацией имеет вид:
, , (- sin ф^
Е ( ф ) = exp ( in ф ) 1 I . (21)
^cos ф J
Световое поле (21) имеет ту особенность, что у него при острой фокусировке продольная проекция вектора напряженности электрического поля равна нулю. В центре светового поля (21) с неоднородной линейной поляризацией имеется V-точка поляризационной сингулярности, в которой не определено направление линейной поляризации. Индекс поляризационной сингулярности V-точки (индекс Винера–Хопфа) равен η = 1. То есть при обходе в начальной плоскости вокруг центра пучка вектора линейной поляризации в сечении пучка поворачиваются на полный оборот.
Все проекции вектора напряженности электрического поля в плоскости фокуса, согласно теории Ричардса–Вольфа [12], имеют вид [16]:
E x = i n -L e in ф [ e^ R ( r ) + e - - ф T ( r ) ] ,
E y = i n e in ф [ e - 'ф R ( r ) - e - i ф T ( r ) ] ,
E z = 0, (22)
R ( r ) = ( 1 0, n +1 + 1 2, n +1 ) ,
T ( r ) = ( 1 0, n -1 + I 2, n -1 ) .
Первые два выражения в (22) можно привести к виду (7), выделив явно проекции векторов большой и малой осей эллипса поляризации в плоскости фокуса:
E = e* ( A + i B ),
A x = 2- [ R ( r ) cos( n + 1) ф + T ( r ) cos( n - 1) ф ] , A y = 2 [ R ( r )sin( n + 1) ф - T ( r )sin( n - 1) ф ] ,
A = 0,
B x = 2- [ R ( r ) sin( n + 1) ф + T ( r ) sin( n - 1) ф ] , B y = 2- [ - R ( r )cos( n + 1) ф + T ( r )cos( n - 1) ф ] , B z = 0,
Y = (n + 1)2.
При выбранном значении топологического заряда n = 1 вместо (23) получим:
A x ,1 = 2 [ R ( r )cos2 ф + T ( r ) ] ,
A y ,1 = 2 R ( r )sin2 ф ,
A z = 0,
B x ,1 = 2 R ( r )sin2 ф ,
B y = 2 [ - R ( r )cos2 ф + T ] ,
B z = 0.
Скалярное произведение векторов A и B будет равно: AB = RTsin (2nφ) /2. То есть вектора будут осями эл- липса поляризации только при n = 0 (азимутальная поляризация). При других n вектора A и B будут лежать в плоскости фокуса, но будут ортогональны между собой только на окружностях некоторых радиусов, когда либо R(r) =0, либо T (r) =0, либо на углах φ = πp/(2n), p = 0,1,2,… . Из (24) следует, что индекс С-точки с круговой поляризацией, которая имеется в центре плоскости фокуса, будет равен Ic =2. Большая ось эллипса поляризации при обходе оптической оси сделает 4 полуоборота, что следует из зависимости проекций вектора A от двойного азимутального угла в (24).
У поля (21) в фокусе будет только продольная проекция вектора СУМ:
S z = 2Im ( E * E y ) =
= 2 ( A * B y - A y B * ) = ( T 2 ( r ) - R 2 ( r ) ) /2.
Так как продольная проекция вектора СУМ (25) не зависит от полярного угла φ, то она будет менять свой знак или будет равна нулю на окружностях определенного радиуса. И распределение интенсивности в фокусе будет иметь радиальную симметрию, I (r)= |A|2+ |B|2 = (R2 (r)+ T 2 (r)) /2. На окружности радиуса r2 в плоскости фокуса, на котором выполняется равенство R (r2) = T (r2), поле (21) в плоскости фокуса имеет линейную поляризацию, так как продольная СУМ (25) равна нулю, Sz =0. Но так как вектора A и B ортогональны друг другу и являются осями эллипса поляризации только на некоторых лучах с углами φ = πp/(2n), p = 0,1,2,…, когда sin(2nφ) = 0, то именно при этих условиях вектор B будет равен нулю и поляризация поля (22) будет линейная. Модули векторов А и В равны при условии, что R (r) T(r)cos(2nф) = 0. То есть на окружностях с центром на оптической оси и с радиусами, при которых либо R (r) =0, либо T (r) =0, либо на углах φ = π /(4n) + πp/(2n), p = 0,1,2,…, световое поле (22) имеет круговую поляризацию (C-линия поляризационной сингулярности). На окружностях в плоскости фокуса с центром на оптической оси, на которых функции |T (r)| > |R (r)| плотность спина Sz будет положительная, и, наоборот, на окружностях, где |T (r)| < |R (r)|, плотность спина отрицательная. Таким образом, мы показали, что для поля (21) в плоскости фокуса продольная компонента спина Sz будет чередовать свой знак. Пусть на некотором радиусе Sz положительная. Далее, при увеличении радиуса, Sz уменьшается и становится равной нулю, и при дальнейшем увеличении радиуса Sz становится отрицательной. Такое поведение продольной составляющей СУМ является проявлением радиального продольного спинового эффекта Холла. Интересно, как при этом ведет себя поверхность эллипса поляризации, лежащая в плоскости фокуса (Az = Bz =0). Если смещаться по радиальной переменной от центра (от оптической оси), то там, где Sz >0, там поверхность эллипса поляризации «смотрит» по направлению оптической оси. Там, где Sz =0, эллипс поляризации сжимается в отрезок (это точка переворота поверхности эллипса). И после этой точки, там, где Sz <0, поверхность эллипса поляризации «смотрит» в обратном направлении оптической оси.
-
5. Моделирование
В этом параграфе с помощью формул Ричардса– Вольфа [12] рассчитаны проекции вектора напряженности электрического поля для некоторых начальных световых полей и распределения интенсивности в плоскости фокуса. Далее по формулам Берри (7) для тех же световых полей рассчитаны координаты векторов большой и малой осей эллипсов поляризации, центры которых лежат в плоскости фокуса. Длина волны – 532 нм, числовая апертура NA=0,95.
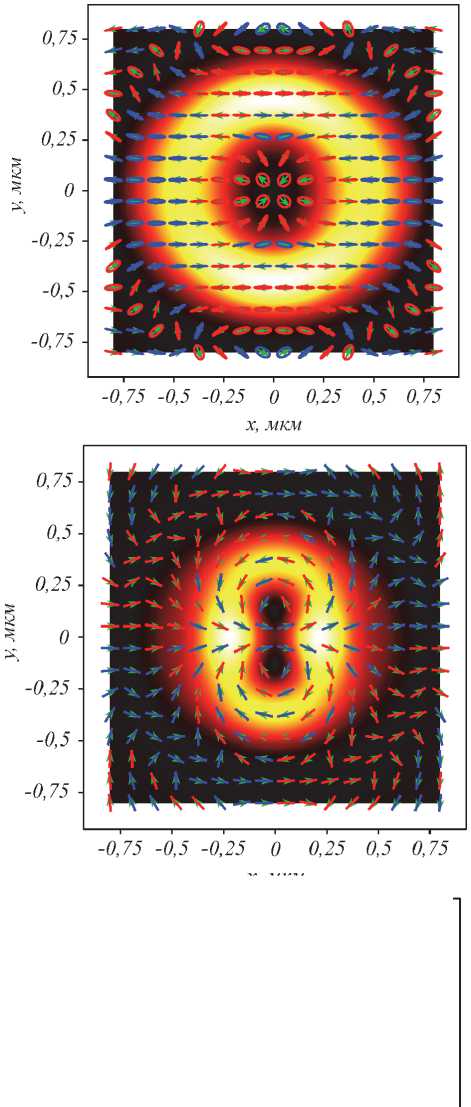
На рис. 1 а показано распределение интенсивности (желто-красное кольцо с неоднородной интенсивностью и немного вытянутое вдоль вертикальной оси) в фокусе для начального поля (1) с n =3. Белый цвет – это максимум интенсивности, желтый цвет – средняя интенсивность, красный цвет – малая интенсивность и черный цвет – нулевая интенсивность. Из рис. 1 а видно, что на оптической оси интенсивность равна нулю, как это и следует из уравнения (6). Из (6) также следует, что в распределении интенсивности будут два максимума на почти круглом кольце, лежащие на вертикальной или горизонтальной оси, в зависимости от знака выражения в круглых скобках, которое умножается на cos(2φ). Так как на рис. 1 а максимальные значения интенсивности лежат на вертикальной оси (белый цвет), то выражение в (6), которое умножается на cos(2φ), отрицательное. Хотя на оптической оси интенсивность равна нулю, вблизи оптической оси поперечную амплитуду поля (2) можно эффективно представить в виде:
(Ex У (^
L * l«- e i ’ 1 2.1 I.I . (26)
I Ey J I iJ
Из (26) следует, что вблизи оптической оси поляризация почти правая круговая. На рис. 1 а внутри светлого кольца интенсивности эллипсы поляризации почти круглые и имеют красный цвет, то есть поляризация правая круговая. Из рис. 1 а видно, что большая ось эллипсов внутри кольца интенсивности при обходе вокруг оптической оси поворачивается на 2π, то есть индекс поляризационной сингулярности поля на рис. 1 а равен Ic = 1. Это также следует из выражения (26), так как топологический заряд поля (1) в фокусе вблизи оптической оси равен 1 (при n =3).
На рис. 1а у желтого эллипса интенсивности видны внутренние и внешние красные краевые эллипсы. На внутреннем красном эллипсе интенсивности вверху и внизу стрелки поляризации синие, а по бокам – стрелки красные. Это означает, что продольная СУМ Sz внутри кольца интенсивности вверху и внизу отрицательная, а по бокам – положительная. То есть имеются четыре об- ласти со спином разного знака – это проявление продольного спинового эффекта Холла. И наоборот, на рис. 1а у внешнего красного эллипса интенсивности сверху и снизу красные стрелки эллипса поляризации, а по бокам – синие. То есть продольная СУМ Sz на внешнем красном эллипсе интенсивности положительна сверху и снизу и отрицательная на боковых сторонах. Опять имеется четыре области со спином разного знака.
а)
в)
-0,75 -0,5 -0,25 0 0,25 0,5 0,75
Рис. 1. Двумерные распределения интенсивности
и нанесенные на них проекции эллипсов поляризации (стрелки и овалы) в плоскости фокуса для начального поля (1), оптического вихря (n = 3) c горизонтальной линейной поляризацией (а); для начального цилиндрического векторного поля (17) второго порядка (n = 2) (б); для поля (21) с топологическим зарядом n = 1 и азимутальной поляризацией (в). Стрелки внутри эллипсов показывают направление большой оси эллипса поляризации. Синие эллипсы имеют левую круговую поляризацию и отрицательную продольную проекцию СУМ (S z < 0), а красные эллипсы имеют правую круговую поляризацию и положительный продольный спин (S z > 0)
При обходе по желтому эллипсу интенсивности в местах перехода от красных стрелок к синим, которые направлены в противоположенные стороны, вектор большой оси эллипса поляризации в 3D-пространстве делает резкий «переворот». При полном обходе по замкнутому контуру вокруг оптической оси вектор большой оси будет формировать 3D-двухстороннюю полоску с четным числом «переворотов», равным числу областей с разным продольным спином. Такая полоска с четным числом полуоборотов называется поляризационной твист-полоской (twisted ribbon) [6].
Еще из рис. 1 а видно, что при обходе по эллипсу примерно посередине желтой интенсивности вокруг его центра направление стрелок большой оси эллипса поляризации меняется на противоположенное 6 раз, равномерно через 60 градусов. То есть при удалении от оптической оси индекс поляризационной сингулярности поля (1) в фокусе равен Ic =3. То есть равен топологическому заряду ( n =3) начального поля (1).
Обратим внимание на 4 синие стрелки в верхней части внутреннего красного эллипса интенсивности на рис. 1 а . Видно, что эти стрелки дважды меняют свое направление на противоположенное. Так как эллипсы поляризации этих 4 стрелок узкие, значит, плоскость этих эллипсов поляризации почти перпендикулярна плоскости фокуса. И так как эти 4 стрелки синие, это значит, что малая ось эллипса поляризации у них направлена против оптической оси, а вектор СУМ почти вертикальный и практически лежит в плоскости фокуса (немного наклонен против оптической оси). Поэтому у двух из этих 4 синих стрелок вектор спина S направлен почти вертикально вверх, а у двух других – вертикально вниз. Такое разделение областей в фокусе с поперечным спином S , направленным в разные стороны (вверх или вниз на рис.1 а ), можно назвать поперечным спиновым эффектом Холла. Эти рассуждения, следующие из рис. 1 а , согласуются с теоретическими выводами, которые следуют из уравнений (13).
На рис. 1б показано распределение интенсивности (сдавленное бело-желто-красное кольцо) в плоскости фокуса для начального цилиндрического векторного поля (17) второго порядка (n =2). Из (18) видно, что интенсивность в фокусе зависит от cos(2φ), и поэтому два максимума интенсивности будут лежать на горизонтальной оси (белый цвет на рис. 1б). В центре распределения интенсивности нет нуля, а есть минимум, пропорциональный слагаемому в (18) I2,0. Из (18) следует, что на вертикальной оси будут две точки нулевой интенсивности, так как при φ = π /2 и φ = 3π/2 поле (18) будет иметь только одну проекцию, отличную от нуля: Ex = i (I2,0 – I0,2), которая будет равна нулю при условии I0,2 – I2,0=0. В этих двух точках у поля (18) имеет место поляризационная сингулярность: V-точки, в которых не определена поляризация. Как видно из рис. 1б, при обходе этих двух точек по за- мкнутому контуру вектор линейной поляризации, как у азимутальной поляризации, поворачивается на 2π. То есть эти две V-точки имеют индекс +1 (верхняя) и –1 (нижняя). Начальное поле (17) при n =2 имело на оптической оси V-точку с индексом 2, а в фокусе эта V-точка распалась на две V-точки, сумма индексов которых равна нулю. Казалось бы, индекс поляризационной сингулярности не сохраняется при фокусировке. Но при обходе по контуру большего радиуса это противоречие устраняется. При обходе оптической оси по внешнему эллипсу интенсивности (по красному эллипсу) вектора линейной поляризации делают два полных оборота (четыре полуоборота), поэтому индекс поля на рис. 1б равен 2 и равен индексу начального поля.
Из рис. 1 б видно, что все эллипсы поляризации лежат в продольных плоскостях и перпендикулярны плоскости фокуса (оптические колеса), поэтому в плоскости фокуса имеются только векторы линейной поляризации (векторы больших осей в эллипсах поляризации). Видно, что в правом верхнем и левом нижнем квадрантах на рис. 1 б в основном имеются синие стрелки, а в левом верхнем и правом нижнем квадрантах имеются в основном красные стрелки. Там, где стрелки красные, правая круговая поляризация и вектор спина S , лежащий в плоскости фокуса, в основном направлен вниз. А там, где стрелки синие, левая круговая поляризация и вектор спина в основном направлен вверх. То есть в плоскости фокуса имеют место области, в которых поперечный вектор спина направлен то вверх, то вниз. Так проявляется поперечный спиновый эффект Холла. Если обходить оптическую ось в плоскости фокуса по окружности (или по эллипсу интенсивности), то часть стрелок поляризации на этой окружности будут направлены по направлению обхода, а часть стрелок – против обхода. Если эти стрелки одного цвета, то вектор спина S будет направлен то внутрь окружности, то вне ее. Если две стрелки, направленные одинаково, имеют разный цвет, то также вектор спина S для одной стрелки будет направлен внутрь окружности, а для другой (другого цвета) – вне окружности. Такое изменение направления вектора спина можно назвать поперечным (радиальным) спиновым эффектом Холла. При обходе вокруг центра в плоскости фокуса есть стрелки, которые перпендикулярны окружности. Если две такие стрелки имеют разный цвет, то вектор спина S у одной из них направлен вдоль окружности (по касательной) по направлению обхода, а у второй – против направления обхода. Если две стрелки одного цвета, но направлены в противоположенные стороны, то также вектор спина одной такой стрелки направлен по направлению обхода, а вектор спина другой стрелки – против. Этот эффект можно назвать поперечным (азимутальным) спиновым эффектом Холла.
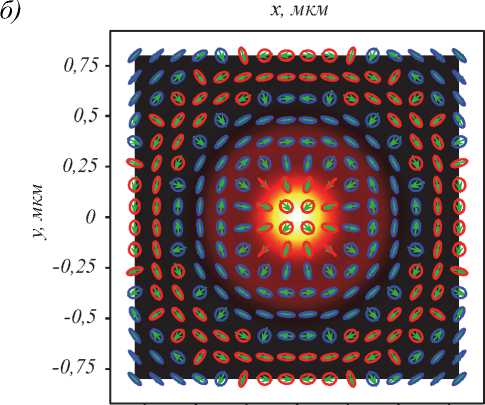
На рис. 1в показаны распределения интенсивности в плоскости фокуса для начального поля (21) с топо- логическим зарядом n = 1. На рис. 1в интенсивность показана в виде круглого фокуса бело-желто-краснофиолетового цвета (бело-желтый цвет – максимальная, а фиолетовый-черный цвет –минимальная интенсивность). Для поля с n = 1 на оптической оси находится С-точка с правой круговой поляризацией, как следует из выражений (22). Индекс поляризационной сингулярности С-точки равен Ic =2. При обходе против часовой стрелки вокруг оптической оси вектор большой оси эллипса поляризации на рис. 1в поворачивается на 4 полуоборота или на 2 полных оборота. Увеличение индекса сингулярности в фокусе для Сточки (Iс =2) по сравнению с индексом поляризационной сингулярности в начальной плоскости для V-точки (η = 1) связано с тем, что топологический заряд оптического вихря (n = 1) в начальной плоскости не влиял на индекс сингулярности поля (21), а в плоскости фокуса оптический вихрь изменил топологию поляризационной картины и увеличил (из-за дополнительных скачков фазы на π) индекс поляризации на 1.
Если смещаться от оптической оси в плоскости фокуса по любому радиусу, то вектор большой оси эллипса поляризации на рис. 1 в будет формировать в 3D-пространстве незамкнутую полоску с полуоборотами на тех расстояниях от оси, где поляризация линейная.
Теоретически и численно показано, что в плоскости фокуса оптического вихря с топологическим зарядом n и линейной поляризацией имеют место следующие оптические поляризационные эффекты. В плоскости фокуса вектора большой оси эллипса поляризации при обходе вокруг оптической оси делают 2n полуоборотов. То есть индекс поляризационной сингулярности векторного поля, состоящего из векторов больших осей эллипсов поляризации с центрами в плоскости фокуса, равен топологическому заряду начального оптического вихря. Независимо от величины топологического заряда в плоскости фокуса будут иметь место 4 области, в которых продольная проекция вектора спинового углового момента меняет знак (продольный эффект Холла). При обходе по замкнутому контуру (окружности, эллипсу) с центром на оптической оси вектор большой оси эллипса поляризации в 3D-пространстве формирует двухстороннюю поляризационную твист-полоску с четным числом полуоборотов, аналогичную twisted ribbon [6]. В плоскости фокуса имеются области, в которых поперечный вектор спина, лежащий в плоскости фокуса, имеет разную проекцию при обходе по окружности (либо по направлению обхода, либо против направления обхода), так проявляется поперечный азимутальный спиновый эффект Холла. Также если при обходе по окружности вектора поперечного спина имеют разную проекцию на радиусы окружности (либо по радиусу от центра, либо по радиусу к цен- тру), то это является проявлением радиального поперечного спинового эффекта Холла.
Работа выполнена при поддержке Российского научного фонда (грант № 22-12-00137) в части теории и по государственному заданию НИЦ «Курчатовский институт» в части моделирования.
ГРНТИ: 29.31.01


