Популяция Олли при антропогенном давлении

Производственная деятельность человека по многим направлениям приводит к нарушению структуры экосистем. Горнорудные производства, химические предприятия, сельскохозяйственная обработка земель, новые транспортные магистрали приводят к уменьшению размеров естественных экосистем. Формировавшиеся многие столетия экосистемы могут быть разрушены в течение нескольких лет, а в случае катастроф по сравнению с длительность их существования c мгновенно. Совместно с естественными природными факторами (наводнения, пожары, землетрясения) на экосистему влияет и человеческий фактор. У популяций, проживающих в экосистемах, есть своя экологическая ниша со своим трофическим ресурсом. Антропогенное давление приводит к уменьшению размеров ниши. Прежде всего, это уменьшение территории проживания и ресурсов, необходимых для обеспечения жизнедеятельности популяций. Часть популяций или их особей покидают экосистему. В результате возникает пороговое значение размера численности популяции, ниже которого популяция выжить не может в новых условиях. Восстановление размеров экосистемы может происходить как естественным путем, так и искусственным – человеком.

Модель одиночной популяции, в которой учитывается медленная скорость роста при малой численности популяции, предложена Базыкиным А.Д. [1]. Однако, эту модель можно рассматривать как частный случай модели популяции Олли [1].

du dt

= ри (u - в)(1 - и),

где р - удельная скорость роста численности популяции, в - пороговое значение численности, ниже которой скорость роста численности становится отрицательной

( 0 <  в <  1 ) . Уравнение (1) имеет три стационарные точки: две устойчивые - и = 0 и и = 1 , и неустойчивую точку и = в .

Антропогенное давление на среду обитания приводит к уменьшению емкости среды и уходу части особей из пораженной экосистемы. С учетом модели антропогенного давле- ния, разработанной в [2, 3], уравнение (1) принимает вид.

du

— = ци и dt

к

—

а —

a1

P

+ P )

1— к

1+bP 1

2 _u

1+b P )

—

P d1u2

d^ + и2 ’

где P - количество загрязнителей, a. , b , b ₂, d , d₂ - параметры.

Предполагается, что в отсутствие антропогенного давления модель (2) переходит в модель одиночной популяции (1), в которой в = 0 . Эффект Олли появляется при наличии загрязнителей среды (при 0 <  P , 0 <  a <  1 ), рассматривается как возникновение стресса в популяции от антропогенного давления. Изменение емкости среды определяется множи-

1 + bP         А телем -—, и при b < b2 емкость умень шается с увеличением количества загрязнителей. Уход особей из загрязненной зоны зада-du    2

ется функцией P------у . и в этом выраже- d2 + и2

нии характеризует групповой уход особей, а гиперболическая зависимость согласуется с экспериментальными данными, приведенными в [4].

Стационарная точка и = 0 уравнения (2) будет устойчивой при появлении загрязните-P лей. При значении и = и = а----- правая

a + p часть уравнения (2) будет отрицательной. То есть в отличие от модели (1) пороговое значение, которое определяет допустимое значение численности популяции, зависит от количества загрязнителей.

Нетривиальные стационарные точки уравнения (2) находятся из решения уравнения.

Ц и к

P

Л

— а---- a + p )

1 —

к

1+bP 1

2 _u

1 + bp )

du

d2 + и2

= 0.

При P = 0 левая часть этого уравнения принимает положительные значения при и > 0, а при достаточно больших значениях P левая часть уравнения (3) становится отрицательной. Поэтому в некотором диапазоне изменения параметра P (0 < P < P) уравнение (3) будет иметь положительный корень. При P = 0 корнем этого уравнения является и = 1. В силу непрерывности левой части этого уравнения от параметра P , оно будет иметь положительный корень близкий к и = 1 при малых значениях P .

Параметры, входящие в уравнение (2), выбираются на основе данных полевых наблюдений, опубликованных в [3, 5, 6]. Уменьшение емкости экосистемы в окрестности горнометаллургических производств, от природных катастроф, по данным опубликованных в [7, 8], может достигать 50%, а покидать загрязненную территорию может до 30% особей популяции. Оценочные значения параметров лежат в диапазонах:

b1 е[1,2], b2 e[3,6], а е[0,1], a1 е[1,2], d2 е[1,2], d 1 е[0.3,1.0]. (4)

N вариантов выбора случайным образом параметров из диапазонов (4) сопоставляется с существованием на загрязненной территории N не взаимодействующих между собой популяций. Размер ниши каждой популяции при антропогенном давлении изменяется независимо от изменения ниш соседних популяций. Аналогичное предположение относится и к скорости ухода особей популяции из экосистемы, и пороговым значениям численности, определяющих начало гибели популяции.

Скорость ухода особей популяции из эко- du 2

системы моделируется функцией P -----у .

d2 + u2

Эта часть популяции переходит в ближайшую экосистему не подверженную антропогенному давлению. Скорость изменения численности v популяции в этой экосистеме описывается уравнением.

dv dt

= pv2 (1 - v) + P

dp2 d2 + u2

Неподвижная точка этого уравнения определяется как корень уравнения

3   2 P du

f ⁽ v ) = v ^- v —J— 2 = 0 .                    (5)

p a2 + u

При v = 0 функция f ( v ) принимает отрицательное значение, ее первая производная обращается в ноль, а вторая производная принимает положительное значение. То есть в этой точке f ( v ) имеет минимум. Поскольку при v ^ —го f ( v ) ^ —го , то максимум этой функции достигается при отрицательных значениях v . С учетом этого при положительных значениях v функция f ( v ) будет монотонно возрастающей функцией.

При v = 1 f ( v ) принимает отрицательное значение. Поэтому единственный положительный корень уравнения (5) лежит при значениях v >  1 . То есть численность популяции во второй экосистеме возрастет за счет притока особей из первой экосистемы.

Имитационное моделирование проводилось путем выбора случайным образом параметров уравнения из диапазонов (4). На рисунке 1 представлено распределение вероятностей численности выживших особей из N = 5000 популяций (зависимость и ). Около 15% популяций считаются погибшими. Распределение суммы выживших особей в двух экосистемах на рис. 1 представлено кривой и + v . Как следует из анализа полученных результатов, медиана покрытия первой системы около 0.5 при проективном покрытии без загрязнения экосистемы равна 1. Для двух экосистем медиана около 1.5. То есть, несмотря на миграцию особей из загрязненной зоны в «чистую» суммарное покрытие не достигает значения 2 – часть особей погибает.

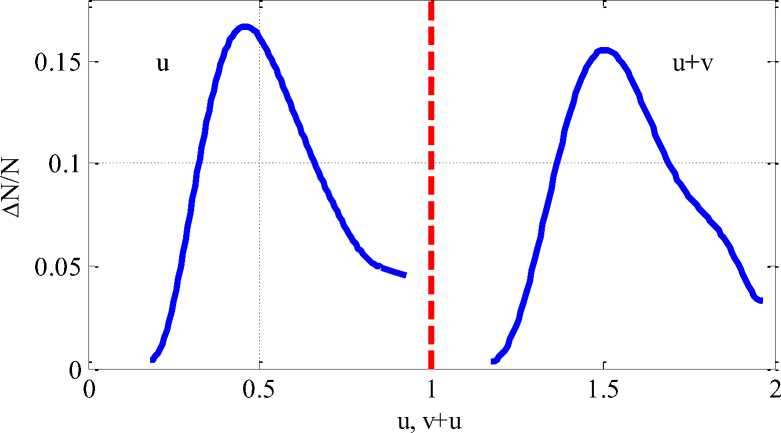
Рис. 1. Распределение вероятностей численности выживших популяций в загрязненной экосистеме, и суммарно в загрязненной и «чистой» экосистемах

Восстановление емкости среды может происходить естественным путем за счет распада загрязнителей, удаления их из среды воздушными и водными потоками. Одновременно с этим происходит и искусственное восстановление экосистемы человеком. Предполагает- dP dt

За начальное условие в этом случае принимается u (t = 0) = 1. На рисунке 2 приведено распределение вероятностей времени начала восстановления численности популяций по ся, что восстановление пораженной территории может начаться сразу после ее поражения. В этом случае считается, что в (2) P является функцией времени и изменяется по закону

-в Р .

мере восстановления емкости экосистемы. Шкала времени на рисунке 2 соответствует неделям.

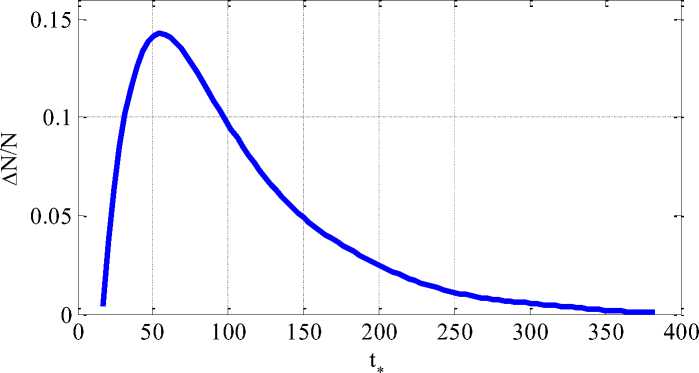
Рис. 2. Распределение вероятностей времени начала восстановления численности популяций

Как следует из анализа полученных результатов, при антропогенном давлении модель (2) прогнозирует гибель около 15% популяций (рис. 1), уменьшение их численности на 50-80%. Наличие соседней «чистой» экосистемы, в которую могут переселяться осо- би, изменяет эти показатели не более чем 10%. Заметное восстановление численности популяций в экосистеме может начаться через 50-150 недель после начала ликвидации последствий антропогенного давления, или последствий природных катастроф.