Пороги цветоразличения и уравнения Эйнштейна

В начале 40-х лет прошлого столетия появились публикации результатов опытов, проведенных Мак Адамом, по выяснению порогов цве-торазличения [1-3]. Аналогичные опыты были также проведены Стайлсом [4], Вышецки [5], а также повторно самим Мак Адамом. Их результаты в целом согласовывались с результатами, полученными изначально Мак Адамом, и графически отображались в виде эллипсов на цветовой диаграмме МКО 1931 г. (x, y). На рис. 1. изображены результаты опытов Мак Адама, которые впоследствии получили название «Эллипсы Мак Адама».

Рис. 1. Эллипсы Мак Адама (для наглядности размеры эллипсов увеличены в 10 раз)

Автором статьи был разработан программный комплекс по измерению порогов цветоразличения

[6], описание которого дано в [7]. Впоследствии этот программный комплекс был изменен. Суть этого изменения в том, что пороги цветоразличения проводились в зависимости от яркости излучения сравниваемых цветов (в процентном соотношении). На рис. 2 показаны результаты эксперимента (график имеет иллюстративный характер).

Экстраполируя кривую зависимости величины порога до значения яркости равной нулю, получим величину порога, равную бесконечности, а точнее, порог, ограниченный кривой цветового локуса. Известно, что при уменьшении яркости включается механизм ночного или сумрачного зрения, то есть в процесс зрения включаются палочки глаза, а колбочки выключаются, как имеющие цветочувствительность в отличие от палочек. Имеет место эффект Пуркунье («ночью все кошки серые»).

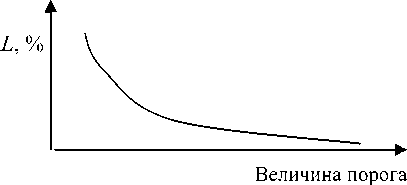
Рис. 2. Зависимость порога цветоразличения от яркости

Но природа «любит симметрию», а это значит, что при увеличении яркости излучения до очень больших значений цветочувствительность глаза также будет уменьшаться. Это явление можно объяснить тем, что распад йодапсина (светочувствительное вещество колбочек глаза) будет происходить быстрее, нежели его восстановление. Глаз станет цветослепым, то есть величина порога цветоразличения будет увеличиваться по мере увеличения яркости излучения, и при очень больших яркостях порог цветоразличения будет равен бесконечности, точнее, эта бесконечность будет ограничена цветовым локусом. Конечно, такая яркость в природе, а тем более в телевидении (на экране монитора) не реализуется и может быть рассмотрена только теоретически. В графическом виде это демонстрирует рис. 3.

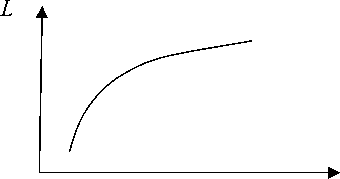
Величина порога

Рис. 3. Зависимость порога цветоразличения при яркости излучения, стремящейся к бесконечности

Теперь посмотрим на картину в целом – она соответствует рис. 4, где изображен однополосный гиперболоид [8]. Далее необходимо ввести некоторые обозначения и определения:

• -    горизонт цвета – под этим будем понимать некую замкнутую поверхность, объем внутри которой, с точки зрения цветоразличения глаза, цветооднородный, изотропный;

• -    бесконечность – область, ограниченная цветовым локусом.

Рассмотрим некоторые области этого гиперболоида. О верхней и нижней частях рис. 4, окрашенных, соответственно, в белый и черный цвета, можно сказать, что горизонт событий уходит в бесконечность. Сами эти поверхности линейны и имеют евклидову геометрию. Более сложную структуру имеет пространство, расположенное в центральной части рис. 4.

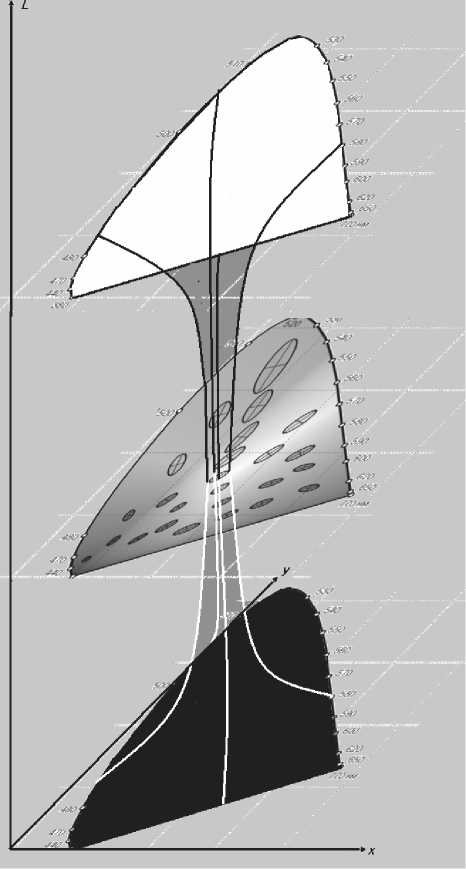
Рис. 4. Зависимость порогов цветоразличения от яркости излучения

Горизонт цвета имеет малый радиус, и это обстоятельство указывает на то, что пространство, заключенное под горизонтом цвета, искривлено и замкнуто – как это имеет место, например, в пространстве черных дыр в фундаментальной теории эволюции звезд (горизонт событий). В связи с этим можно для определения порогов цветовосприятия, а также для создания новых равноконтрастных цветовых систем, где все эллипсы Мак Адама трансформировались бы в одинаковые окружности, а в трехмерном пространстве – в шары одинакого диаметра, применить фундаментальную общую теорию относительности А. Эйнштейна. Для описания центральной части полученного однополосного гиперболоида можно использовать уравнение Эйнштейна [9].

В общей теории относительности (ОТО) встречается название – «уравнения гравитационного поля», связывающие между собой метрику искривленного пространства-времени со свойствами заполняющей его материи. Этот термин используется и в единственном числе: «уравнение Эйнштейна», так как в тензорной записи это одно уравнение, хотя в компонентах оно представляет собой систему уравнений.

Выглядят уравнения Эйнштейна следующим образом:

n Я . 8^6'

Rab ~^gab+ Mab = —~ Tab > (1) 2 c где Rab – тензор Риччи, получающийся из тензора кривизны пространства-времени ^abcd посредством свертки его по паре индексов; R – скалярная кривизна, то есть свернутый тензор Риччи; Sab – метрический тензор; Л – космологическая постоянная; Tab представляет собой тензор энергии-импульса материи; с – скорость света в вакууме; G – гравитационная постоянная Ньютона. Так как все входящие в уравнения тензоры симметричны, то в четырехмерном пространстве-времени эти уравнения равносильны скалярным уравнениям. Одним из важных свойств уравнений Эйнштейна является нелинейность, приводящая к невозможности использования при их решении принципа суперпозиции.

Как видно из (1), в правой части используются такие физические константы, как гравитационная постоянная Ньютона скорость света, которые в нашем случае должны быть заменены на функции, характеризующие цвет: цветовой тон, насыщенность и яркость. Это же относится к тензору энергии-импульса материи Tub . В левой части уравнения, очевидно, для нашего случая космологическая постоянная л = о, тогда уравнение (1) примет вид

где Цт – цветовой тон; Ц H – цветовая насыщенность; L – яркость цвета.

Эти цветотехнические параметры могут быть измерены, например, с помощью прибора [10].

Очевидно, что правую часть (2) можно представить неким «цветовым тензором», поскольку Цт’Чн ^и т можно записать в векторном представлении (для случая определения порогов цве-торазличения). С учетом этого перепишем (2) в следующем виде:

R_ab--g_ab=sc_ab, (3)

где S – некоторая константа. Авторами [7; 11] предпринимались весьма удачные разработки равноконтрастных колориметрических систем, в которых эллипсы Мак Адама трансформировались в почти равновеликие окружности в криволинейной системе координат, построенной на основании применения метрического тензора. Кроме того, в [7] предложена трехмерная система координат, в которой изображены шары равного диаметра.

Уравнения Эйнштейна описывает четырехмерное пространство-время, которому соответствует наше трехмерное цветовое пространство. Но кто знает, как эволюционирует глаз человека во времени? В том, что он развивается и, естественно, меняется, сомнений нет, но вопрос в том, как именно это происходит? Можно сделать следующее предположение: когда появился человек, Земля была покрыта в большей части зеленью, и максимальная чувствительность глаза соответствовала зеленой области спектра – эта тенденция сохранилась и по сей день. Но поскольку первобытный человек был по натуре охотником, его глаз должен был видеть в ближней инфракрасной области спектра, то есть глаз должен был видеть и тепловое излучение животного мира. Исходя из этих предположений, цветовой локус стандартного наблюдателя в то далекое время должен был быть растянут в красную и близко инфракрасную области спектра – поэтому вполне допустимо, что синяя область спектрального диапазона была урезана.

Как дальше пойдет развитие глаза человека, сказать трудно. Но, тем не менее, можно рассматривать и четырехмерное цветовое пространство-время в уравнении (2), приняв временной интервал равным нулю, что соответствует современной эпохе.

В настоящее время, согласно литературным данным, существует большое число решений уравнения Эйнштейна. Решить уравнение Эйнштейна – значит найти вид метрического тензор пространства-времени. Существуют также чисто математические классификации решений, основанные на топологических свойствах, описываемого ими пространства-времени, или, например, на алгебраической симметрии тензора Вейля данного пространства. Заметим, что рис. 4 очень похож на результат решения уравнения Эйнштейна, полученный Шварцшильдом [12] для пространства-времени, изображенного на рис. 5 при интервале времени Т = 0.

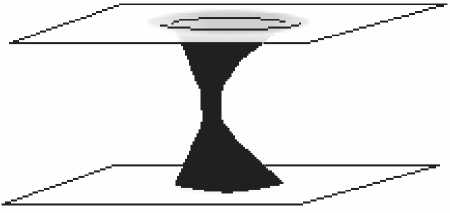
Рис. 5. Сечение пространства Шварцшильда при Т = 0

Свое решение Шварцшильд получил для черной дыры, не имеющей электрического заряда, при отсутствии вращения: данное решение оказалось пространством-временем Миньковского с топологиейR-xS и метрикой ds2 = - 1c2d/2 + 1dr2 +

V r)             r)            (4)

+ f" {дв' + sin² бдф¹).

Здесь координата r принимает только значения, большие F_$ . Важно, что значение параметра F, в отличие от лапласовского случая, не является «расстоянием до центра» – центра в шварцшильдовском решении вообще нет. Геометрический смысл этого значения состоит в том, что площадь поверхности сферы

{(t,F,0,(p^t = t0,r = r0} равна 4й02.

рически симметричное тело с радиусом, пре-C^F вышающим F и массой M---^ , где обоз-на чения прежние Замечательно чения прежние. Замечательно, что величина гравитационного радиуса – радиус Шварцшильда Fs совпадает с гравитационным радиусом Tg’ вычисленным ранее Лапласом для тела массы M.

В заключение можно сделать вывод о том, что соединение фундаментальной физики ОТО с вопросами порогов цветоразличения может породить новые равноконтрастные цветовые системы, в которых известные эллипсы Мак Адама будут превращены в одинаковые по диаметру окружности, а для цветов получены одинаковые шары.