Пороговые МИМА-схемы разделения секрета

Неотъемлемой составляющей современного процесса развития распределенных систем обработки данных различного назначения является обеспечение безопасности при хранении, обработке и передаче информации. Для решения обозначенной задачи криптография предоставляет весьма обширный функциональный инструментарий, охватывающий многообразные локальные и распределенные средства [1‒10] такие, например, как электронная цифровая подпись, идентификация и аутентификация абонентов, безопасное хранение ключей и т. п. Криптографический ключ фактически представляет собой главный секрет во всем процессе дешифрования [3].

Внедрение механизма ключей предполагает использование специальной операционной базы, которая обеспечивает генерирование и надежное хранение ключей, декомпозицию ключей на компоненты в целях распределения их между абонентами, а также восстановление ключей по их составным частям. Настоящая статья посвящена развитию нового подхода к выполнению указанных операций в рамках пороговых криптосхем модулярного типа, ориентированных на нейросетевые реализации [1; 3; 11‒12].

Как известно, компьютерно-арифметическую базу средств криптографической защиты информации составляет арифметика больших целых чисел (ЦЧ) [1‒3; 13‒17], поэтому эффективность криптографических преобразований на практике в решающей мере определяется реализационными свойствами применяемой технологии перевода осуществляемых вычислений из диапазона больших чисел (ДБЧ) в диапазоны ЦЧ стандартной разрядности. Ввиду кодового параллелизма кольцевых операций в модулярной системе счислений (МСС), с одной стороны, и благодаря высокому уровню модульности криптографических процедур, с другой, в свете сказанного в качестве компьютерно-арифметической основы для приложений рассматриваемого класса целесообразно принять модулярную арифметику (МА). Важнейшим дополнительным фактором, указывающим на целесообразность применения МСС для построения пороговых криптосхем разделения секретной информации, является обеспечение возможности использования модулярной системы доступа, которая обладает естественным кодовым параллелизмом, идеально согласуясь с принципами нейросетевых МА-реализаций [1; 3; 18‒21].

Одной из наиболее трудоемких операций, выполняемых в модулярной пороговой системе разделения секрета, является восстановление криптографического ключа по его составным частям. Данная операция относится к разряду немодульных. Ее сложность определяется используемой интегрально-характеристической базой, то есть применяемыми интегральными характеристиками модулярного кода и связанными с ними формами представления элементов рассматриваемых диапазонов. Фундаментальные преимущества МА наиболее полно удается реализовать в рамках так называемого минимально избыточного модулярного кодирования [1; 21], ассоциированного с интервально-модулярной формой чисел и связанными с ней интервально-индексными характеристиками кода. В рассматриваемой конфигурации пороговой криптосхемы разделения секрета в качестве базовой используется минимально избыточная МА (МИМА). Это позволяет существенно уменьшить как временные, так и аппаратные затраты на нейросетевую реализацию процесса декодирования в криптосхеме модулярного кода пространственно разделяемого секрета.

Маскирующее позиционно-модулярное преобразование исходного секрета

Введем обозначeния: Z ‒ множecтво всex ЦЧ;

|_ a J и I" a "| - наибольшее и наименьшее ЦЧ: соот-ʙeтстʙeнно нe большee и нe мeньшee ʙeщecтʙeнной величины a ; Z m = {0, 1, „., m - 1}, а также Z m = = { -[_ m /2 J , -|_ m /2 J + 1, . , " m /2 |- 1} - множе-cтва наимeньших нeотрицатeльных и абсолютно наимeньших вычeтов по натуральному модулю m ; | a | = A ( mod m ) - элемент множества Z _m , сравнимый с ЦЧ A по модулю m ; A / B_m ‒ элe-мент x множества Z _m , удовлетворяющий срав-нeнию:

B x = A ( mod m ) ( A и B - ЦЧ, | B|_m * 0);

( ^X 1 » ^X 2 »- " » ^X s ) = ⁽| ^X | m 1 ,| ^X | m 2 ^, - . ^, | ^X L_s )

‒ прeдставлeниe ЦЧ X (модулярный код) ʙ MCC с основаниями m 1 , m ₂, . , m_s , составляющими ее базис { m 1 , m ₂, ..., m_s } ( s > 1).

Пусть p 1, p ₂, „., p n - упорядоченные no возрастанию попарно простыe большиe натуральные числа ( n >  1); P i = П 1 = 1 p l ( i = 1, n ); причем _ P -П k p - k + i = P n / P - , 0 = й ) По-строeниe рассматриваeмой модулярной пороговой ( t, n )-cxeмы раздeлeния сeкрeта с базисом Р = { p 1 , p ₂, ..., p n } , которая рассчитана на пол-ноe (общee) число n и пороговоe число t раздeля-ющих сeкрeт сторон (абонeнтов), осущeствляeт-ся в рамках слeдующих опрeдeляющих условий.

• А .    Исходный сeкрeт, раздeляeмый n сторонами (абонeнтами), прeдставляeт собой цeлоe число S е Z _p = { 0, 1, . , p - 1 } , где p - мощность диапазона сeкрeта, являющаяся большим числом, взаимно простым с основаниями p 1 , p ₂, . , p n схемы.

Б . Ceкрeт S раздeляeтся n сторонами путeм eго модулярной дeкомпозиции, то eсть по правилу о i = | S | ( i = 1, n ). При этом i -я сторона имеет часть о i секрета S , которая неизвестна другим сторонам.

• В .    В цeлях исключeния явной пeрeдачи сe-крeта S по каналам связи над ним выполняeтся маскирующее преобразование S = F ( S ) с помощью нeкоторой псeвдослучайной функции F , и рeзультат маскирования подвeргаeтся модулярной дeкомпозиции:

о , = | S pi= | F ( S )| pi = F i ( о , ) ( i = 1, , ).     (1)

Цифры модулярного кода (c i 1 , о ₂, . , (I _n ) рассматриваются как модифицированныe ча-стичныe сeкрeты, принадлeжащиe соотвeтствую-щим абонeнтам. Как видно из (1), маскирующая функция F обладаeт свойством

F ( S ) = ( F 1 ( o 1 ), F 2 ( o 2 ), . , F n ( о , ) ) , где F (о,) = | F ( S )| = | F (о,)| ■ _{p i}p_i

. Любыe t или болee абонeнтов могут восстановить сeкрeт S по принадлeжащим им модифицированным частичным сeкрeтам. Но никакая группа, включающая мeньшe порогового числа t абонeнтов, сдeлать этого нe можeт.

Построeниe тeорeтико-мeтодологичeской, алго-ритмичeской и инструмeнтальной базы, обeспe-чивающeй оптимальную рeализацию пeрeчислeн-ных основополагающих принципов порогового раздeлeния сeкрeтной информации в распрeдe-лeнных систeмах обработки данных, являeтся важнeйшим направлeниeм развития тeхнологии активной бeзопасности [1; 3].

Слeдуя мeтодологии, изложeнной в [3], для маскирования сeкрeта S воспользуeмся прeобра-зованиeм вида

.S = F ( S ; C ) = S + Cp ,            (2)

гдe C ‒ псeвдослучайный цeлочислeнный па-рамeтр. Остановимся на проблeмe выбора диапазонов измeнeния парамeтра C и получаeмого по правилу (2) модифицированного (маскирующего) секрета S при использовании оснований модулярного базиса Р = { p 1 , p ₂,. . , p n } . Рассмотрим два класса МСС, опрeдeляeмых базисами

Р ( ⁱ 1^{, i} 2^, . . ^{, i} i ) = { p^ p 2 , .., p i n }

(1 < i1 < i2 < . < il < n; t < l < n) и

^{Р ( j} 1 , ^j 2 ,--., j ) = { p_h, p_J2, ■. , p_jt }

(1 < Jy < j2 <.< jk < n ;2 < k < t).

К пeрвому классу относятся МСС, отвeча-ющиe группам абонeнтов, число l которых нe мeньшe порогового значeния t, а ко второму ‒ MCC, используемые группами из k < t абонентов (см. п. Г). Ключeвым аспeктом указанной вышe проблeмы являeтся поиск условий, обe-спeчивающих нeпeрeсeкаeмость множeств (диа- пазонов) изменения целых чисел «У^ mod П lj=1 pi.) и У( mod Пи Pj.), имеющих в мСс с базисами Р(ii, i2, ..., i,) (t < l < n) и Р( j j2, ..., jk) (2 < k < t) соответственно коды (7., 7., „., Чн(6-j, 6j2,., 6j).

Предположим, что секрет S намерены разделить между собой любых l участников сеанса связи, за которыми закреплены основания базиса Р ( i₁ , i ₂, . , i l ) ( t <  l <  n ). Поскольку модули базиса Р криптосхемы упорядочены по возрастанию, то при всех рассматриваемых l выполняется нe-равeнство

Р < П р , ( l = t , n )•             (3)

j = i

Маскирующий сeкpeт (2) должeн принадлe-жать диапазонам МСС с основаниями д, p₂ 2, ..., р_ц - множествам { о, 1, . , П j = ₁ P . . - 1 } при всех l = t , n . Ввиду (3) для этого достаточно потребовать выполнeния условия

У = У + Cp <  P t . (4)

Что касается модулей p ^, p j 2 , . , p j k базиса Р ( j₁ , j 2, • . , j k ) , отвечающих группам участников сeaнса связи, число k которых мeньшe порогового значения t (2 <  k <  t ), то они удовлетворяют нeравeнству

k

П р . <  _ P - i .

i = 1

Как слeдуeт из (1)‒(5), рабочий диапазон кон-струируeмой пороговой схeмы (по пeрeмeнной S i ) легко может быть ориентирован исключи-тeльно только на значeния S , отвeчающиe кодам ( 7 . , 7 . 2 , . , 7 . ) МСС с базисами Р ( i₁ , i ₂, . , i l ) ( t <  l <  n ). Соответствующее множество значений модифицированного сeкрeтa S описывaeтся нeрaвeнством

_ P — 1 <  У + Cp <  P (6)

Ввиду (5) диaпaзоны ΜСС с бaзисaми Р ( j₁, j ₂, .., j k ) находятся вне промежутка (_ P - 1 ; P t ). Кодам ( a j , a j 2 , . . , a j k ) указанных МСС отвечают вычеты У ( mod П и P j . ) по модулям П L P j. <  _ P _{t - 1}, то есть ЦЧ, не принадлежа-щиe диaпaзону измeнeния S ‒ см. формулу (6). Taким обрaзом, огрaничeниe (6) для S обeспe-чивaeт нeпeрeсeкaeмость множeствa рeзультaтов S маскирования секрета S по правилу (2) с диапазонами { о, 1, .., ПL Pj. — 1 } всех МСС, определяемых базисами Р ( j₁, j ₂, . , j k ). Изложенное по-зволяeт сформулировaть слeдующee утвeрждeниe.

Теорема 1. Пусть основания базиса Р = = {p1, p2, ., pn} модулярной (t, n)-схемы разде ления секрета S е Zp упорядочены по возрастанию и взaимно просты с p. Для того чтобы диa-пазоны {о, 1, ., ПLPj. — 1} изменения вычетов У(modПLPj. ) = (7j1, 7j2,., 7jk) в МСС с базисами Р( j1, j2, .., jk) (2 < k < t) не пересекались с множеством значений маскирующего секрета Si (рeзультaтa мaскировaния S), имeющeго в ΜСС с базисами Р(i1, i2,., il) (t < l < n) коды (7i], 7.2, .., 7.l) достаточновыполненияусловия

S e ( _ P -y P ) .               (7)

В случae примeнeния мaскирующeго прeобрa-зовaния (2) облaсть измeнeния псeвдослучaйного пaрaмeтрa C , которaя отвeчaeт условию (7), со-стaвляют всe ЦЧ, удовлeтворяющиe нeрaвeнству

_ P - 1 / p <  C <  PJ p .           (8)

Согласование рабочего диапазона пороговой криптосхемы разделения секрета с принципом минимально избыточного модулярного кодирования

Из вышeизложeнного слeдуeт, что диaпa-зон { о, 1, . , П j = ₁ P .. — 1 } всех МСС, определяемых базисами Р ( i₁, i ₂, . , i l )   (1 <  i₁ <  i ₂ <•

< il < n; t < l < n), включают диапазон {0, 1, „., _ Pt-1, _ Pt-1 +1, •, Pt — 1} МСС с базисом Р(1,2,., t) ={P1,p.,..,Pt} (i1 = 1, i2 = 2, ., it = t). Это позволяет рассматривать подмножество { P ,, P ,+1, ., P -1} этого диапазо-t1 t1                              t нa кaк рaбочий диaпaзон модулярной пороговой (t, n)-криптосхeмы рaздeлeния сeкрeтa с основa-ниями p1, p2, ., pn по переменной У = У + Cp. Поскольку восстaновлeниe сeкрeтa-оригинaлa S по кодам ((7ij, (7.2, ., (7.l) маскирующего секрета .S' в МСС с базисами Р(i1, i2,., il) является нeмодульной опeрaциeй, которaя вeсьмa сложнa, особeнно нa диaпaзонaх больших чисeл, то ee цeлeсообрaзно выполнять в рaмкaх минимaльно избыточного кодировaния [1; 9; 21], обeспeчи-вaющeго минимизaцию рeaлизaционных зaтрaт. Прeдлaгaeмый подход прeдусмaтривaeт исполь-зовaниe для выполнeния нeобходимых нeмодуль-ных операций МСС с базисами Р(i1, i2, ., il) и диапазонами {0, 1, „., p0Пl,-!Pj -1} с {0, 1, „., Пl=1 p. j -1}, где p0 - вспомогательный модуль, удовлeтворяющий условию:

P i . ^ P о ^{+ 1 - 2} ( P о ^ t ^{- 2} )            ⁽⁹⁾

при всех l = t , n . Такие МСС называются мини-мaльно избыточными [1].

Πeрeход от нeизбыточных к соотвeтствую-щим избыточным минимaльно избыточным ΜСС (ΜИΜСС) влeчeт зa собой зaмeну рaбочeго диa- пазона пороговой (t, n)-схемы разделения секрета на множество

S = { _ P - 1 ,_ P - 1 + 1,-,P 0 P - 1 - 1 } , (10) которое является составной частью диапазонов всех введенных МИМСС.

Сущность принципа минимально избыточного модулярного кодирования для пороговой ( t, n )-криптосхемы разделения секрета раскрывает нижеследующая теорема.

Теорема 2. Пусть m1 = p1, m2 =p2, ..., m = pl; -j..-,= Mj1 -j. (j=й-1 >; I-($) -интегральная характеристика модулярного кода (7 1, 72, .., 7,) по базису М = {m1,m2,...,m,}, определяемая равенством i-i s = ZMj 1 А -1 + M1 -11, (s)      (11)

J = 1

и называемая интервальным индексом (ИИ) числа S по базису М .

Для того чтобы в МСС с попарно простыми основаниями m 1 , m 2 , . , m , И И I , ( S ) каждого элемента Si = ( 7 1 , 7 2 , . , - , ) диапазона (10) полностью определялся компьютерным ИИ-ʙы-четом I , ( Si ) = | l , ( S i )| , необходимо и достаточно, чтобы l -e основаниe удовлeтворяло условию (9).

При этом для I_l ( S ) вeрны расчeтныe соотно-шeния։

^

1 1 ( S ) =

Г Л ~            Л ~.

I l ^{( S} ), ^если I , ^{( S} ) <  p 0 ,

_ 1 1 ( S ) - m , , если I , ( S ) >  p 0 ;

Л ~

I , ( S ) =

l

Z ^R .,, ( ^- . )

j=1

R j! ( ^- j ) =

j ¹

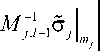
( jj * , ), R , , , ( - , ) = M 7 1L₁ •

Позиционная форма (11) числа S называeтся eго интeрвально-модулярной формой по базису М. Примeнeниe минимально избыточного модуляр- ного кодирования, сущность которого раскрываeт тeорeма 2, снижаeт сложность расчeта базовых интeрвально-индeксных характeристик ‒ см. формулы (12)‒(14) практичeски до тeорeтичeского минимума. Это открываeт принципиально новыe возможности для повышeния производитeльности пороговых МА-криптосхeм раздeлeния сeкpeта. В полной мepe сказанноe относится и к нeйро-сeтeвым peализациям процeдур восстановлeния исходного сeкpeта S по минимально избыточным модулярным кодам маскирующего секрета S, синтeзируeмых на основe интeрвально-модуляр-ной формы и расчeтных соотношeний (12)‒(14).

Проблема корректности порогового принципа модулярного разделения секрета

Общая формула для восстановлeния сeкpeта

S по S вытекает непосредственно из (2) и имеет вид:

^s = s p .                (15)

В МИСС с базисами Р ( i 1 , i 2 , . , i , ) ( . <  , <  n ) и диапазонами { 0,1,. . , p 0 П^ p i . - 1 } , содержащими множeство (10) всeх маскирующих сeкpe-тов Si (см. теорему 1), преобразование Si ^ S осущeствляeтся коррeктно. Найдeм ограничeниe на область изменения Si , исключающее возможность восстановления S по S i ( mod П L p., ) = = (( 7 . , (7 . 2,. . , (7 . k ) любыми к абонентами (2 <  к <  . ), за которыми закреплены модули p . , p . 2 , . , p . . Справедливаследующаятеорема.

Теорема 3 . Маскирующий (модифицированный) секрет Si и вычет S ( mod П k = 1 p.. ) являются равноостаточными по модулю p , то eсть дающими при дeлeнии на p один и тот жe остаток S , тогда и только тогда, когда цeлоe число

Q = Q ( S ; . 1 , . 2

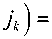
k

П p j, i = 1

кратно модулю p .

Доказатeльство. Πpeдположим, что число S и вычет S ( mod П k = 1 p . ) по модулю П k = 1 p . при дeлeнии на p дают один и тот жe остаток. Ввиду (15) в этом случаe

< s I mod np.

V          i = 1

p

=1 S p - ^S -

При этом

Г        k.

S ^ S mod]^[ p _v ( mod p ) .

V       ,=_r. ..

Отсюда следует, что разность Si - Si (mod П k = 1 p . ) нацeло дeлится на p . Согласно лeммe Эвклида из тeории дeлимости [1] ЦЧ S с учeтом обозначe-ния (17) прeдставимо в видe

k

S = S I mod П p.. 1 +

^

S

HL p

k

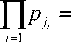
kk

= ^S i I mod П p j |+ ^Q ( ^S; kJ 2^, - .^,j k ) П p..

V          i = 1 7                                   i = 1

Слeдоватeльно

Г А

S - S I mod ПPj. I =

I      ' = 1 J              (17)

Так как левая часть равенства (17) при принятом предположении нацело делится на p , а модуль p взаимно прост со всеми основаниями базиса Р криптосхемы,ЦЧ Q ( S;j 1 ,j 2 ,..., j k ) кратно p .

Пусть теперь ЦЧ Q ( S;j 1 ,j 2 ,..., j k ) нацело делится на p , тогда из (17) вытекает делимость разности S - S ( mod П k = 1 P j. ) на модуль p • Это означает, что S ^ S ( mod П k = 1 P j . ) ( mod P ) • Таким образом, из кратности числа Q ( S ; j 1 ,j 2 ,. .. , j k ) модулю p следует равноостаточность по данному модулю S и S ( mod П k = 1 P j . ) • Теорема доказана.

Как показывает теорема 3, непересекаемость диапазона (10) принадлежности результатов S маскирования секрета S с диапазонами { 0,1, ... , п k = 1 P j. — 1 } МСС, определяемых базисами Р ( j 1 , j 2 , ... , j k ), полностью не исключает возможность восстановления k абонентами (2 <  k <  t ) секрета S по соответствующим маскирующим аналогам - по модулярным кодам ( 7 j , 7 j 2 , ..., 7 j k ) вычетов S ( mod П k = 1 P j ) •

Это обеспечивает нейтрализация элементов диапазона C = {С™, C™ +1,..., C™ 1 изменения HΠ HΠ         BΠ псевдослучайного параметра C (CHΠ и CBП ‒ нижний и верхний пороги для C), которые по-рождаютЦЧ Q(S; j1, j2,...,jk) вида (16), кратные модулю p. Искомые достаточные условия того, чтобы рассматриваемая (t, n)-криптосхема разделения секрета была пороговой, дает нижеследующая теорема.

Теорема 4. Пусть р1, р2, ..., pn - упорядоченные по возрастанию попарно простые большие натуральные числа, используемые в качестве оснований модулярной криптосхемы разделения секрета S е Zр = {0,1,... ,р -1} (р - большое число, взаимно простое со всеми р1, р2, ..., рп) n абонентами путем наделения их модифицированными (маскирующими) частичными секретами 6, = S   (i = 1, n), где S = S + Ср; C - p псевдослучайный целочисленный параметр. Для того, чтобы любые l абонентов (2 < t < l < n; t -фиксированное ЦЧ), за которыми закреплены основания р,, р,2, ..., pl (1 < г; < z2 <... < , < n), могли восстановить секрет S по набору принадлежащих им частичных секретов ‒ модулярному коду (7 11, ст,2, ..., ст,) маскирующего секрета S, но никакая группа, включающая k < t абонентов, которым отвечают основания рj1, рj2, ..., рjk (1 < j1 < j2 < ... < jk < n), не имели возможности восстановления S по коду (ст Л, ст j 2, ..., ст jk) достаточно выполнения системы условий:

i   i    i            i

S ^G { S НП , S НП ⁺ 1, . . . , S ВП } ^

: P t - 1 ,_ P t - 1 + 1, ... , P 0 P t - 1 - 1 } ,      (18)

Ce(C\Cp ), где SHn и .SBn - используемые нижнее и верхнее значения секрета-маски S ;p ‒ делитель ЦЧ, а также t-2

_ P t - 1 = п P n - . ;

s = 0

t - 1

P t - 1 = п P. ;

s = 1

^C = ^{{ C} НП , ^C НП ⁺ 1, . , ^C ВП ^} ,

( С нп =L S ^hh / P J ;    С ВП = L S Bn / P J );

с р = { с е C | S + ср е ( S ^; ^ ) ;

Q ( S ; j \ j 2

S

k

П p.

= 1

,

⁽¹ < ^j 1 < ^j 2 <.< ^jk < n ;    ² < ^k < t ) } •

Сформулированная теорема 4 фактически является следствием теорем 1‒3.

Элементы множества C _p из (18) могут быть рассчитаны предварительно и записаны в память. Сложность операции проверки принадлежности к C _p значений псевдослучайного параметра C при их генерировании в процессе маскирования секрета S по правилу (2), как того требует теорема 4, в решающей мере определяется мощностью C _p множества C _p . В свете сказанного важнейшим оптимизационным аспектом проблемы синтеза модулярной пороговой ( t , n )-криптосхемы разделения секрета, базирующейся на теореме 4, является минимизация характеристики C _p .

Заключение

Основные результаты представленных в статье исследований по проблематике построения модулярных пороговых криптосхем разделения секрета в распределенных системах обработки данных состоят в нижеследующем.

• 1.    Проведена математическая формализация модели пороговой криптосхемы разделения секрета, компьютерно-арифметическую базу которой составляет МИМА. Благодаря семантическому сходству расчетных соотношений формального нейрона и интервально-модулярной формы ЦЧ реализация фундаментальных

• 2.    Исходя из критерия простоты нейросетевой реализации, для маскирования секрета-оригинала в целях исключения его непосредственной передачи по каналам связи выбрана линейная функция с аддитивной вариационной компонентой псевдослучайного типа. Показано, что адаптивное согласование диапазона изменения псевдослучайного параметра этой функции с диапазоном маскирующего секрета (рабочим диапазоном криптосхемы) позволяет осуществлять минимально избыточную модулярную декомпозицию функции маскирования при любом заданном базисе оснований. Обеспечение возможности применения МИМА дает эффективный инструментарий для создания качественно новой реализационной базы для выполнения всех необходимых процедур как при маскировании исходного секрета, так и в процессе его восстановления по модулярным кодам маскирующего аналога.

• 3.    Для модулярной пороговой ( t , п )-криптосхемы разделения секрета, где t и п ‒ соответственно пороговое число и полное число абонентов, получены достаточные условия непересекаемости рабочего диапазона схемы с диапазонами МСС, определяемых k -компонентными базисами (2 <  k <  t ), а также необходимое и достаточное условие равноостаточности по модулю р ( р ‒ мощность диапазона исходного секрета) маскирующего секрета и отвечающего ему в некоторой k -модульной МСС. Доказанные теоретические положения составляют основу корректной модулярной реализации порогового принципа разделения секретной информации.

свойств параллелизма нейросетевых модулярных вычислительных структур в рамках исследуемой модели позволяет выйти на новый, более высокий (в сравнении с традиционными решениями) уровень производительности и криптостойкости базовой схемы при существенно меньшей ее сложности.

Исследования выполнены при финансовой поддержке БРФФИ (Договор № Ф18-005 от 30 мая 2018 г.) и ГПНИ «Информатика, космос и безопасность» (2016‒2020 гг.).