Porous material deformability in four-roll pass rolling

It is mostly imperative for modern material swaging theory to develop mathematical models and matching methods of calculation of plastic shaping and compacting parameters. This is entirely true for new technique of sintered powder rod rolling in four-roll passes. Presently, such rods made of tungsten and molybdenum powders by their pressing and two-stage sintering are treated basically by swaging. But experimental investigations and commercial production practice evidently show technological and ecological advantages of four-roll pass rolling technique over swaging. Owing to such a situation, there is an urgent need for thorough experimental and theoretical investigations of plastic shaping and sintered powder material compacting at the zone of deformation during the rolling with four-side reduction. Besides, such investigations would be critical for improving existing technologies and developing up-to-date methods of rod rolling with four-side reduction of the rod at the zone of deformation.

Model of powder rod compacting in rolling

Basing on previous experimental data concerning the nature of powder sintered rod compacting at the zone of deformation during the process of four-roll rolling, authors have proposed the following analytic functions describing den- sity changes in a powder strip along the entire length of its deformation zone [1]:

рСх) = (Р о - P l ) (- f ) + P l ,          (1)

where ро, р1 are rod densities before and after the rolling, respectively, l is the length of deformation zone, k is the parameter of deformation degree, its values being set as follows: k = 0 if ρ = const, k = 1 if the degree of deformation ε is less than 40%, and k = 2 if ε is greater than 40%.

Another analytic function [2] is expressed as:

P(x) = Р о ” f( ^ ^ )^+[1—C ^ ^^ ]|,      (2)

\ p0 L pO -I L where n is the parameter characterizing the rate of powder rod compacting in the direction of rolling; this rate being inversely proportional to rod density at the given profile of deformation zone.

However, the latest complex experimental investigations of plastic shaping character and powder rod compacting at the zone of deformation in the process of rolling with four-side reduction have revealed that the proposed functions (1) and (2) fail to describe properly the real nature of changes in sintered powder rod density along the entire length of deformation zone. The above functions just set a trend for possible monotonic changing in rod density and leave the question of what degrees of that monotony would be at each separate point of the entire length of deformation zone.

The g oa l wa s to obt a in a mor e a c c ura t e e xp r e s sion f or de ns ity dis trib utio n in s in te re d powd e r r od a l ong the l e ng th of d e f o r ma ti on zone. The exper ime ntal inv e st ig a ti ons ha v e be e n carrie d o ut t o solv e th e pr o bl e m using unde r r ol led molybdenum powde r r od s obtaine d by r ol ling i n four-r oll pa s se s. Du r i ng the e xpe rime nt, t he c h aracter of step-by-s te p c ha ng ing in c r oss-section area was also observed.

I ndust r ial t e st s of th e f o l lowing tec hni que wer e a l so ca rr i e d ou t. T her e we re s e l e c t e d the sample s f r om the batch of sin ter ed pure mol ybdenum pow der r ods w ith 18 ×18 m m c r oss s ect i o n area an d 6 0 0 mm l en gt h h avi ng t h e s m allest diff er enc es in de ns it ies of th e ma te r i a l f a r a n d wi de . The sele ctio n of sa mple s wa s car rie d ou t in t wo w ays: by h y dr owe ig hing and radioisotopic d e nsi ty me a sur ing wit h th e he lp of spe cial devi c e [3] , per mitti ng to me a sure de nsi ty c har a ct er i st ics i n powder s int e r e d r od s so a s to g a in in f orma tio n about the a v e r a g e de ns ity i n the r od at a def in it e cross- se c tion ar e a a s we l l a s d e ns ity distribution o ve r that a re a or le ng thw i se . T he above de v ic e utilizes gamma- ra dia tion s our c e, i ts principl e o f o pe r ati on basing on r e g is tr ati on o f c hang e s i n collimated gamma- ra y b ea m p as s i n g t h ro u gh ga m ma a bsor be r , e . g . sin te re d powde r r od. T h e device offers ±0.1 g/cm³ ac cur a c y of de ns ity me asurements.

F rom the selec ted powder r ods under r o l le d rods wer e pr od uc e d by r ol ling on f our-roll pass industrial mill MK- 2 10×4, a t the UZ B EK R e f ract or y Metals C ombine . T h e unde rr ol le d r od s we re subjected to different de g r ee s of d e f o r ma tion , namely, 25 %, 30%, 33 % a nd 36% [1] and edge re ducti on. S p e c i a l g uid e s he ld the r od s oh thei r edges dur i ng the r e d uc t ion . T he u nder r o ll e d si nt e re d powder r od s we re c u t in to c r o ss 1 a nd lo ng it udin a l 2 te mpla tes ( F i g . 1) to s tudy their macro- an d m i cro s t ru ct u re s an d t o m easu re t he d e nsity o f r od ma ter i a l alon g the e nt ire leng th o f deformation zone.

The changes in material density values along the zone of sintered powder rod deformation were measured by hydroweighing of cross templates, and the changes in rod cross-section area magnitudes along the length of deformation zone were observed by BMI-1 microscope. The character of density distribution ρ( x ), over the material, and rod cross-section areas S ( x ) along the length of deformation zone were approximated by the following analytic functions:

р(х) _ Р о [1 + ^(1 - f ) ” • exp (у)], (3)

S(%)_S o [1 — s(1 — 7pexp ф], (4) where n and m are exactly the parameters whose values are found as a result of data processing by least square method.

Setting x equal to zero one can find density values ρ 1 and cross-section area magnitudes S 1 at the outlet of rod deformation zone:

P i _ р(0) _ P o (1 + Л),                 (5)

S₁=S(G) = S o (1-B).              (6)

Introducing δ ρ as relative rod compactness after rolling:

g _ ^p l ^-p 0

and δS as relative reduction of rod cross-section area:

^g S

S o -S i

S o ,

one can rewrite functions (3) and (4) with respect of (5), (6), (7) and (8) equations as follows:

p ⁽o ^_ P o ^[1 + 5 p ^{(1 -} Y ⁾ⁿe^xp ⁽Y^)],     ⁽⁹⁾

5(%)_5 o [1-6_s(1- y )^mexp ( =5^ )]. (10)

With regard to the law of constant mass of the material under plastic shaping and compacting, one can find the relationship between parameters of original rod and rolled strip:

(1-6 s )A p (1 + 6 p )_1,             (11)

where Л _ — is the strip elongation in one pass, ^p L o

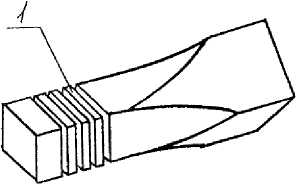
Fig. 1. Cross 1 and longitudinal 2 underrolled rod templates

Барков Л.А., Каменщиков Ю.И., Самодурова М.Н., Латфулина Ю.С.

Деформируемость пористого материала при прокатке в четырехвалковом калибре

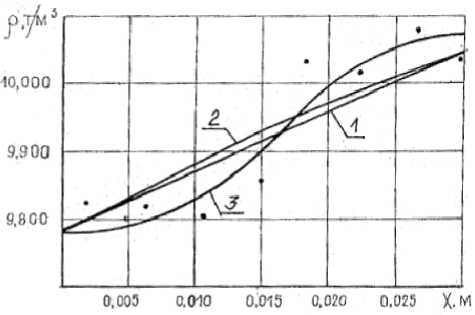
Fig. 2. Powder rod compacting curves. Data taken along the entire length of deformation zone in the process of rod rolling. Straight line 1 is the plot of function (12); Curve 2 is the plot of function (2) when n = 20; Curve 3 is the plot of function (9); (•) are experimental points

L 0 and L 1 are rod lengths before and after the rolling, respectively.

With respect to the relative compactness δ ρ , formula (11) can be expressed as:

⁵ P    (l-5_s)A_p    ^{1 .}

Formula (12) clearly shows that deform a tion parameters are interrelated, i.e. knowing the va lues of any two of them one can easily find the third one from (12). For instance, as geometrical parameters δ S and λ ρ can be directly found from the experiment, then the value of parameter δ ρ is obtai ned from formula (12), thus avoiding labour- consuming experiment for d e termination of the character of density distrib u tion in powder rod along the length of its d eformation zone.

Basing on experimental data obtained the va lues of n and m parameters in eq uations (9) and (10) were calculated according to the standard computer approximation program by method of the least squares. Calculation results and exper imental data are plotted in Fig. 2.

Thorough analysis of curves behavior in Fig. 2, which are plotted according to the above functions (12), (2) and (9) against experimental data points, reveals function (9) to be the most real description of powder compacting character along the length of deformation zone, while functions (12) and (2) show just a qualitatively monotonic character of compacting. This provides for a further application of function (9) to powder material plastic compacting at the zone of its deformation in rolling with four-side reduction.