Постановка и исследование динамических задач в модели разработки газового месторождения
Автор: Скиба А.К.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 3 (55) т.14, 2022 года.
Бесплатный доступ
Рассматривается непрерывная агрегированная динамическая модель разработки газового месторождения. Ставятся, решаются и исследуются две математические задачи. Одна является прямой задачей оптимального управления с фиксированным временем и со свободным правым концом. Другая - обратная задача. При фиксированном оптимальном управлении осуществляется поиск горизонтов планирования. Предлагается алгоритм численного поиска всех горизонтов планирования.Задачи подвергаются всестороннему анализу. Основным математическим аппаратом является принцип максимума Понтрягина. Используется теорема существования и дифференцируемости неявной функции.
Агрегированная модель газового месторождения, прикладная задача оптимального управления со свободным правым концом и фиксированным временем, прямая и обратная задачи, максимизация накопленной прибыли
Короткий адрес: https://sciup.org/142236620
IDR: 142236620 | УДК: 519.86
Текст научной статьи Постановка и исследование динамических задач в модели разработки газового месторождения
В настоящее время Россия находится в стадии экономического подъема. Значительный народнохозяйственный рост обеспечивается многочисленными факторами. К ним можно отнести:
-
• огромную территорию Российской Федерации, большая часть которой располагается в умеренном поясе;
-
• наличие значительных сельскохозяйственных угодий, обеспечивающих продовольственную безопасность страны;
-
• наличие значительных трудовых ресурсов, которые обеспечиваются за счет населения страны и излишка рабочих рук в соседних с Россией государствах;
-
• запасы произведенного капитала в стране (здания, машины, оборудование, инфраструктура, городские земли);
-
• сильный научно-технический потенциал;
-
• высокий уровень образования;
-
• большие запасы полезных ископаемых и др.
К полезным ископаемым относятся минеральные и органические образования в земной коры. Химический состав и физические свойства полезных ископаемых позволяют эффективно использовать их в сфере материального и нематериального производства. По агрегатному состоянию полезные ископаемые находятся в твёрдой, жидкой или газообразной фазе.
В разных уголках нашей планеты, начиная с момента образования Земли, сформировались различные полезные ископаемые, которые составляют природные богатства стран мира. Такое формирование наблюдается и в Российской Федерации. В ней имеется огромное множество мест, где находятся существенные скопления полезных ископаемых. Наличие значительного количества полезных ископаемых подтверждено геологоразведочными работами и их извлечением из недр Земли. Можно с большой уверенностью утверждать, что в недрах России содержится практически вся таблица Менделеева.
В ряду всех российских полезных ископаемых особое место занимает природный газ [1, 2]. Природный газ является ценным минералом, и он относится к невозобновляемым ресурсам. Данное полезное ископаемое, представляющее собой смесь газообразных углеводородов природного происхождения, состоит главным образом из метана и примесей других алканов.
Природный газ может существовать в виде газовых залежей, находящихся в пластах некоторых горных пород. Помимо залежей газа в недрах планеты, интересно упомянуть, что углеводороды встречаются и в космосе. В частности, метан является третьим по распространенности газом во Вселенной после водорода и гелия. В форме метанового льда он входит в структуру планет и других космических тел. Однако такие образования не относят к залежам природного газа и при настоящем уровне развития технологий не могут быть извлечены.
Главным образом природный газ используется для обеспечения отопления, производства электроэнергии и для бытовых нужд населения. В России около 50% поставок приходится на энергетические компании и коммунальное хозяйство. Кроме этого, природный газ находит применение в качестве топлива для транспортных средств, сырья при производстве пластмасс и других органических веществ.
Методы добычи газообразных углеводородов схожи с добычей нефти - газ извлекают из недр с помощью скважин. Для того чтобы пластовое давление залежи падало постепенно, скважины размещают равномерно по всей территории месторождения. Такой метод также препятствует возникновению перетоков газа между областями месторождения и преждевременному обводнению залежи.
Наша страна имеет возможность добывать природный газ в значительных объемах в течение достаточно длительного времени, обеспечивая не только внутренний рынок, но и внешних потребителей, гарантируя им долгосрочные устойчивые объемы поставок этого важного продукта. Однако места добычи и поставок потребителям природного газа находятся на достаточно больших расстояниях, превышающих иногда тысячи километров. В большинстве случаях для доставки газа потребителям используется газопровод, который ограничивает пропускную способность поставляемого продукта. Данное ограничение существенно, и его необходимо учитывать при добыче природного газа из залежей [3].
В этой связи возникают математические задачи, которые представляют научный интерес и базируются на соответствующих моделях. Ряд задач уже решен и нашел свое практическое применение, другие задачи ожидают своего анализа. В отделе математических методов регионального программирования ФИЦ ИУ РАН ведутся исследовательские работы по математическому моделированию эксплуатации нефтяных и газовых месторождений [4-6]. Рассматриваемые модели подвергались различным модификациям и всестороннему изучению. На этих моделях ставились и решались разнообразные оптимизационные задачи. В отделе также изучались динамические модели, которые в дальнейшем применялись для численных расчетов при решении многих практических задач.
Среди всех оптимизационных задач, поставленных и решенных, нам бы хотелось выделить две из них: задача максимизации накопленной добычи для группы газовых месторождений с ограничением на пропускную способность газопровод [3] и задача максимизации длины их общей «полки» [7]. Для их решения применялся принцип максимума Понтрягина в форме Эрроу [8].
Первая из приведенных задач имеет экономическое содержание, как максимизация совокупного дохода для группы газовых месторождений. Можно поставить и другие оптимизационные задачи с экономическим содержанием. К ним относится минимизация затрат и максимизация прибыли.
1. Построение модели, постановка и решение прямой математической задачи
Рассматривается динамическая модель разработки газового месторождения с взаимо-влияющими скважинами [5-7]. Вводятся следующие обозначения:
Т - горизонт планирования;
t - текущее время (0 > t > Т );
Q(t) - текущая добыча газа;
-
q(t) - средний дебит добывающих скважин в момент t;
-
q° - начальный средний дебит добывающих скважин;
-
n(t) - количество скважин, вводимых в строй в единицу времени;
-
n(t) - максимальные возможности по вводу в строй новых скважин;
N (t) - действующий фонд добывающих скважин в момент t;
-
N 0 - начальный фонд добывающих скважин;
-
V(t) - извлекаемый запас газа, оставшийся в залежи в момент t;
-
V 0 - начальный извлекаемый запас газа;
-
6 - коэффициент дисконтирования;
-
с - продажная цена природного газа;
-
к - стоимость строительства одной скважины.
Между переменными мы устанавливаем зависимости, представленные в виде системы обыкновенных дифференциальных уравнений:
N = n(t),(1)
q° q = - V0 q(t)N(t) = -«q(t)N(t),(
-
V(t) = -Q(t) = -q(t)N (t),(3)
при ограничении
0 < n(t) < n(t),(4)
с начальными условиями
-
V0 > 0,(5)
q0 > 0,(6)
N 0 = 0.
В описании дифференциального уравнения (2) мы вводим дополнительное обозначение:
a = q°/V 0.
Дополнительно мы делаем следующие предположения:
-
• в любой момент t газовое месторождение покрывается равномерной сеткой добывающих скважин;
-
• управление динамическим процессом разработки месторождения осуществляется за счет ввода новых скважин n(t) с учетом ограничения (4);
-
• бурение скважины и ввод ее в разработку месторождения происходят в один и тот же момент времени.
Задача 1. О максимизации накопленной прибыли с учетом коэффициента дисконтирования для одного газового месторождения
Для системы дифференциальных уравнений (1) - (3) с начальными условиями (5) - (7) и фиксированного интервала времени [0,Т] необходимо найти функцию n(t), удовлетворяющую ограничению (4), и соответствующую этой функции траекторию (q(t),N (t)), которая доставляет максимальное значение функционалу
т
[cQ(t) — kn(t)] exp[— 5t] dt. (9)
Правый конец оптимальной траектории (q(t),N (t)) считаем свободным. Функция n(t) в двойном неравенстве (4) является постоянной величиной равной значению п > 0. В этом случае двойное неравенство (4) представится в следующей форме:
0 < n(t) < п, п > 0. (10)
Обратим внимание на взаимосвязь дифференциальных уравнений (2) и (3). Действительно, фазовые переменные q(t) и V(t) линейно зависят друг от друга при любых допустимых управлениях, т.е. q(t) = aV(t) Поэтому в дальнейшем при исследованиях достаточно ограничиться только двумя фазовыми переменными q(t) и N(t). К управляющим параметрам относится только одна переменная n(t).
В описании накопленной прибыли (9) был включен коэффициент дисконтирования 5, позволяющий соизмерять доходы и затраты, производимые в различные моменты времени. Сформулируем и докажем следующую теорему.
Теорема 1. Оптимальное управление n(t) в задаче максимизации накопленной прибыли на фиксированном временном промеэюутке [0, Т] существует и единственно. Оптимальное управление n(t) при дополнительном ограничении cq0[1 — exp(—5T)]/5 > к принимает следующий вид:
(П)
-(t) = Г п пPut 6 [0,Т], Т 6 (0,Т)> [ 0 при t 6 (т, Т].
Доказательство. Рассматриваемая задача 1 является задачей оптимального управления со свободным правым концом и фиксированным временем. Существование оптимального управления следует из теоремы, приведённой в монографии [9, §4.2]. Доказательство единственности мы приведем в конце доказательства теоремы 1.
Для решения этой задачи мы используем принцип максимума Понтрягина в классической формулировке [10,11]. Введем сопряжеиные переменные i^(t) и у (t), относящиеся к фазовым переменным q(t) и N (t) соответственно. Согласно принципу максимума Понтрягина выпишем гамильтониан
Н(q, N, п, ф, у) = cqN — kn — ^aqN + уп.
В каждый момент t Е [0, Т] управление n(t) на оптимальной траектории максимизирует гамильтониан
Н(q(t),N (t),n(t),^(t),^(t)) = max Н(q(t),N (t),n,^(t),y(ty). (14)
n£ [0 ,n ]
Из (13) и (14) вытекает:
п при у (t) > k,
n(t) = <
0 при у (t) < k,
0 < n(t) < n при у (t) = k.
Сопряженные уравнения представятся в виде
|
■ дН , . _ , _ ф = 5ф = 5ф — cN + ^aN, |
(16) |
|
- . дН ; у = оу - dN = ^^ - cq + ^aq. |
(17) |
На правых концах сопряженных переменных ^(t) и у (t) выполняются условия трансверсальности:
^(Т ) = у(Т ) = 0.
Пусть в момент t Е [0,Т] выполняется неравенство c < a^(t), тогда из (16) и поло жительности ^(t) следует дальнейшее возрастание сопряженной переменной ^(t). Условия трансверсальности (18) нарушаются. Значит, c > a^(t) при всех t Е [0, Т].
Рассматриваем всевозможные сопряженные переменные ^(t) и y(t). Среди функций ^(t) и у (t) выделяем сопряженные переменные, удовлетворяющие условиям трансверсальности (18). Из (16) видно, что при отрицательном значении ^(t) вытекает невыполнение условия трансверсальности (18). Следовательно, сопряженная переменная ^(t), соответствующая оптимальной траектории, неотрицательна. Если N(Т ) = 0, то ^(t) = 0 при t Е [0,Т].
Если выполнено условие на оптимальной траектории N(Т) > 0, то справедливо двойное неравенство 0 < ^(t) < c/a при t Е [0,Т) и ^(Т) = 0. Докажем, что сопряженная переменная y(t) положительна. Умножаем левую и правую части сопряженного уравнения (16) на q и после несложных преобразований с учетом (2) получаем d£ (N = 5^q - cqN.
Умножаем обе части дифференциального уравнения (19) на exp(— 6t) и после несложных математических операций интегрируем обе части полученного равенства от t до Т. Учитывая условия трансверсальности (18), приходим к соотношению
^(t)q(t) exp(— 5t) = c / q(0)N(Ө) exp(— 5Ө) d3.
В силу положительности q(t) и N(Т ), непрерывности и неотрицательности N (t) вытекает, что интеграл в правой части равенства (20) положителен. Отсюда положительна сопряженная переменная ^(t) при t Е [0, Т) и ^(Т) = 0. Если N(Т ) = 0, то из (20) вытекает
—(t) = 0 пр и t Е [0,Т ]. Принимая во внимание (2), преобразуем (19). В результате получаем следующее дифференциальное уравнение:
4[(— — — )q exp(—St)] = —qexp(-5t). at a a
С учетом условия трансверсальности (18) интегрируем обе части полученного соотно шения (21) от t до Т:
[--— (t)]q(t) exp(— St) = —q(T )exp(— ST ) +-- q(Ө) exp(— SӨ) AB. (22)
a a a t
Правая часть равенства (22) положительна. Значит, — (t) < ^ .
С сопряженным уравнением (17) проделаем те же операции, что и с уравнением (16).
После всех преобразований решение сопряженного уравнения (17) представится в виде интегрального выражения:
^(t) = / [c — a— (Ө)]q(Ө) exp[— S(Ө — t)] аӨ.
Отсюда следует, что сопряженная переменная y(t) положительна на полуинтервале t Е [0,Т). Умножаем обе части сопряженного уравнения (16) на q, и после преобразований с помощью (2) получаем
— [a—q — cq] = Sa—q.
Продифференцируем по t обе части сопряженного уравнения (17) и, подставив в полученное выражение (24), приходим к следующему дифференциальному уравнению второго порядка:
у —
S = aS—q. (25) Умножаем обе части дифференциального уравнения (25) на exp(—St) и после преобразований с учетом (2), (17) и (18) проинтегрируем от t до Т полученный результат: y(t) = у(Т) exp[—S(T — t)] — Sa J —(Ө)q(Ө) exp[—S(Ө — t)] гіӨ = = —cq(T )exp[—£(Т — t)] — Sa / — (Ө)q(Ө) exp[—6(6 — t)\dB. Отсюда следует, что сопряженная переменная y(t) строго убывает. Рассмотрим случай N(Т) = 0, тогда у(0) < k, —(t) = 0 и q(t) = q0 при всех t Е [0, Т]. Из (23) вытекает следующее нестрогое неравенство: cq0[1 — exp(—ST)]/S < к. (26) В противном случае при N(Т) > 0 выполняются соотношения (11) и (12). Переходим к доказательству единственности оптимальных управлений. Общая схема доказательства единственности состоит в следующем. Преобразовываем формулу (23) для определения сопряженной переменной y(t) и устанавливаем зависимость у(т). Доказываем строгое убывание функции у(т). Убеждаемся, что у(т = 0) > к л у(т = Т) = 0. Следовательно, уравнение у(т) = к имеет на отрезке [0, Т] одно решение, что приводит нас к единственности оптимальных траекторий. Для дальнейшего упрощения вида формул мы надчеркивание у параметра й опускаем. Пусть решение задачи 1 описывается формулой (12). В этом случае с учетом (1), (2), (6) и (7) общий фонд добывающих скважин и дебит скважин изменяются следующим образом: N(t) = | nt при t Е [0,т], т Е (0, Т), пт при t Е (т, Т]; Г q° exp[—ant2/2] при t Е [0, т], т Е (0, Т), [ q° exp[an(т2/2 — tт)] при t Е (т,Т]. Представим в формуле (23) сопряженную переменную при т< t< Т в виде разности двух интегралов: ^(t) = I cq(9) exp[—8(9 — t)] d9 — а ^ ^(9)q(9) exp[—8(9 — t)] d9 = G1(t) — G2(t). (29) С учетом (1), (2), (7) и (12) преобразуем функцию Gi(t): Gi(t) = / cq(9) exp[—8(9 — t)] d9 = —q^ {1 — exp[—(апт + 8)(Т — t)]}. (30) Jt апт+8 С учетом (27), (28) и т< t <Т преобразуем соотношение (20): ^(t)q(t) = cq(t)nт {1 — exp[—(апт + 8)(Т —t)]}. апт + 8 Отсюда при т< t< 9 <Т получаем ^(9)q(9) exp[—8(9 — t)] = cq^ т {1 — exp[—(апт + 8)(Т — t)]} exp[—(апт + 8)(9 — t)]. (31) апт + 8 Используя предыдущее соотношение, преобразуем функцию G2(t) из (29): G2(t) = а IT^(9)q(9)exp[—8(9 — t)] d9 = .cq(t)аnT {1 — exp[—(апт + 8)(Т — t)]} — J t (апт + 8)2 — cq(t)anт (т — t) exp[—(апт + 8)(Т — t)]. (32) апт + 8 С учетом (30) и последнего выражения (32) для G2(t) перепишем функцию (29): V(t) = Cq(t) е{1 — eXP[—(anT + 8)(Т — t)]} — Cq(t)an-T2{1 — exP[—(anт + 8)(Т — t)]} + апт + 8 (апт + 8)2 cq9t^anт +---(Т — t) exp[—(апт + 8)(Т — t)]. апт + 8 В последнее выражение (33) подставим (28) при t = т. В результате получаем ф(т) = cq°e ,—апт2 ----[1 — е-(“"-+^)(т--)] + (апт + 8)2 аптг(Т — т)е-(апт+5)(т-т)}. (34) апт + 8 Продифференцируем функцию ф(т): ^т —canтq0 е—апт2/2{81 е-(апт+<5)(Т—т) (апт + 8)2 + апт(Т — т)е-(аПт+5)(Т—т)} + апт + 8 +cq0e—апт2/2{— (ап)2т(Т( —^)^T+5)(T Т) + апт(Т — т)е—(апт+5)(Т—т) — т[ап(Т — т)]2е — (аГ1т+6)(Т-т)+ап(Т — т)е — (апт+5)(т-т)—апте — (аПт+8)(Т-т) апт + 8 апт + 8 апт + 8 28ап[1 - е-(апт+8)(т-т)] (апт + 8)3 8е-(апт+8)(т-Т) 8ап(Т - т)е-(апт+5Кт-т) апт + 8 (апт + 8)2 Докажем, что <^Т < 0 ПРит Е [0,Т]. Все члены математического выражения разбиваем на три непересекающиеся группы. Каждую группу мы отделяем фигурными скобками с положительным множителем. Дополнительно введем обозначения функций Іі(т), І2(т) и ^з(т ) <^Т = саптд°е апт2/2{-8- _ е—(«пт+8)(т-т) (апт + 8)2 - апт(Т - т) е-(апт+8)(т-т)+(Т_т)е-(апт+8)(т-т)} + апт + 8 +сд0е-апт 2/2{ ап(Т - т)е-(апт+8)(т-т) апт + 8 8ап(Т - т)е-(апт+8)(т-т) (апт + 8)2 28ап[1 - е-(апт+8)(т-т)] (апт + 8)3 (ап)2т(Т -т)е (апт+8)(т т) } + 0 -апт2/2{-т[ап(Т - т)]2 - -I 4 -(апт+8)(т-т) (апт + 8)2 } + СЧ е {апт + 8 -}е = = саптд0е апт2/2Іі(т) + сд0 е-апт2/2І2(т) + сд0е-апт 2/2-(апт+8)(т-т )Із(т). (36) Функция Із(т) отрицательна, т.к. она содержит только отрицательные члены. Покажем, что функции Іі(т) и І2(т) отрицательны при т Е [0,Т]. Действителыю: Іі(т) = -8- е-(апт+8)(т-т) (апт + 8)2 - апт (Т - т)е- (апт+8)(т-т) апт + 8 + (Т - т)е-(апт+8')(т-т) = X, -(апт+8)(т-т) (апт + 8)2 ^^-т) - 1 - + 8)(Т - т)]< 0 І2(т) = ап(Т - т)е-(апт+8^(т-т) апт + 8 8ап(Т - т)е-(апт+8')(т-т) 28ап[1 - е-(апт+8)(т-т)] (апт + 8)2 (апт + 8)3 (ап)2т(Т - т)е-(апт+8)(т-т) (апт + 8)2 28ае-(апт+8)(т-т) (апт + 8)3 [е(апт+8)(т-т) -1 -(апт+8)(Т-т)] < 0. Значит, функция у(т) строго убывает на отрезке [0, Т]. Убеждаемся, что у(т = 0) > к II ^(т = Т) = 0. Поэтому уравнение ^(т) = к имеет единственное решение т > 0. Следовательно, найденный параметр т однозначно единственным образом определяет оптимальные управления. Единственность и теорема 1 доказаны.
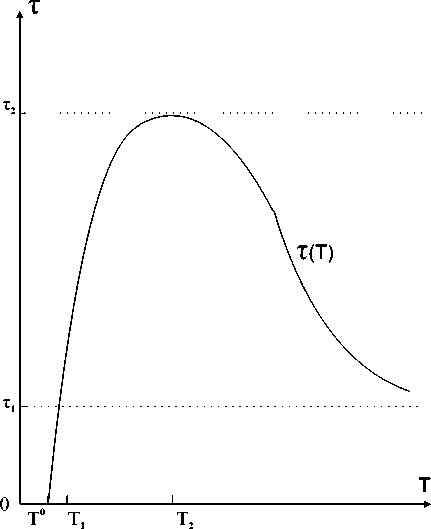
2. Постановка и исследование обратной оптимизационной задачи В предыдущем параграфе мы доказали, что при дополнительном условии (11) оптимальное управление имеет вид (12). Это означает ограничение на сопряженную переменную ^(0) > к. Было доказано, что ^(/) - строго убывающая (функция и ^(Т) = 0. В момент t = т осуществляется переключение с одного режима разработки месторождения на другой режим. В этот момент ^(t = т) = к. Сопряженная переменная y(t), учитывая свойства переменных (27) и (28), преобразуется и далее она рассматривается как функция ^(т). Доказывается, что построенная функция ^(т) строго убывает. При этом выполняются два соотношения: ^(т = 0) > к и ^(т = Т) = 0. Следовательно, существует единственное решение уравнения ^(т) = к. Значит, единственными являются не только оптимальное управление (12), но и соответствующие ей фазовые переменные (27) и (28). Поставленная задача 1 состоит в максимизации накопленной прибыли (9) на интервале [0, Т]. Анализ исходных параметров задачи показывает, что при выборе конкретного числового значения горизонта планирования Т наблюдается некоторый произвол. Действительно, иногда трудно аргументированно объяснить, почему мы выбрали это, а не другое значение рассматриваемого параметра. В то же время числовые значения других вышеупомянутых параметров модели имеют более четкую аргументацию. Они определяются исходя из технологических, экономических и других причин, связанных с изучением конкретного месторождения. В работе [12] исследовалась следующая ситуация. Два газовых месторождения участвуют в конкурсе на право первым начать свою разработку. Поражение в конкурсе приводит к нежелательным последствиям и значительным материальным и финансовым потерям. Основным критерием выбора является минимум себестоимости. При расчете себестоимости учитывается прогнозная добыча газа в течение заданного количества лет Т. Данная информация берется для каждого месторождения из проекта разработки. Было показано, что в некоторых случаях при одних значениях горизонта планирования Т в конкурсе побеждает первое месторождение, а при других - второе месторождение. Возникает конфликтная ситуация с соответствующими последствиями. Поэтому нам необходимо обратить больше внимания на горизонт планирования Т . Основное решение задачи максимизации прибыли формулируется в виде теоремы 1. Переформулируем теорему 1 следующим образом. Теорема 1’. В задаче 1 с фиксированным временем Т оптимальное управление (12) и соответствующие фазовые переменные (27) и (28) однозначно определяются параметром т. Данный параметр т существует и принимает при условии (11) единственное значение внутри отрезка [0, Т ]. Пара метр т определяется из решения уравнения ф(г) = к, где функция ф(т) задается равенством (34). Сформулируем обратную задачу. Задача 2. Пусть фиксирован строго полоэюителъный параметр т и при этом значении т однозначно определяются управление (12) и фазовые переменные (27) и (28). Найти все значения Т > т, при которых управление (12) будет оптимальным для задачи 1. Необходимо таксисе ответить на вопрос о существовании искомых решений. Заметим, что любая оптимальная пара (т, Т), где 0 < т < Т, однозначно определяет оптимальное управление (12). Дальнейший анализ показывает, что для фиксированного значения т таких горизонтов планирования Т может быть не более двух. Воспользуемся равенством (34) и условием Дт) = к, фиксируем оптимальный параметр т и будем искать значение Т из следующего уравнения: ДТ) = cq°e 9 ,-апт2 / _ , [1-е (апт + 5)2 (апт+6^Т-т)]+апт (Т-тИ ”ап+6^Т-т)} = к. (37) апт + 5 Введем обозначение и вычислим s = к(апт + 5)2„пт 2/2 cq°5 Введем вспомогательную функцию /(Т) = 1 - е-(апт+5)(Т-т) + апт(апт + 5)(Т - т)е-(апт+5)(Т-т)/5. (39) Исследуем функцию /(Т) при условии Т > т. Заметим, что от величины т до значения Т2 = т + „1т рассматриваемая функция возрастает. В точке Т2 она достигает своего максимального значения и далее падает. В этих точках функция принимает следующие значения: /(т) = 0;/(Т2) = 1 - exp(-' ) + аД+° exp(- ' ) = 1 + ^ exp(-1 - ). апт о апт о апт У(го) = 1. Такое же последнее значение функция принимает при Ту = т + „пт(„пт+5)< Т2, т. е. / (Ту) = 1. Рис. 1. График вспомогательной функции f(Т) при фиксироваином значении т > 0 На рис. 1 изображен график вспомогательной функции f (Т) при фиксированном значении т > 0. Схематично на нем выделены три области. Если s > f (Т2), то для рассматриваемого значения т не существует оптимального горизонта планирования Т. Это означает, что не существует пары (т, Т), относящейся к оптимальному управлению. Если s = f (Т2), то имеется единственньій период планирования Т = Т2, при котором согласно теореме 1 данная пара (т, Т2) однозначно определяет оптимальное управление. Если s Е (f (Т1),f (Т2)), то имеются два пер иода планирования Ту и Т2 , при которых согласно теореме 1’ пары (т, Т’) и (т,Т2) однозначно определяют свое оптимальное управление. При этом Ту Е (Т,Т2) II Т2 Е (Т2, то). Если s Е (0, f (Ту)), то существует единственный горизонт планирования Т‘ Е (т, Ту), при котором пара (т,Т‘) однозначно определяет единственное оптимальное управление. Таким образом, мы выделили области, в которых лежат оптимальные значения горизонтов планирования Т. На рис. 1 в плоскости (Т, у) прямая линия у = f (Т2) делит положительный квадрант на две части: одна часть содержит хотя бы одно оптимальное значение Т. в другой части оптимальное значение горизонтов планирования Т отсутствует. Прямая линия у = f (Т2) является опорной прямой к графику гладкой функции f (Т) в точке ее оптимума. Продолжим исследование оптимальных решений задачи максимизации дисконтированной прибыли. Для этого воспользуемся представлением переменных т и Т в виде уравнения (37): <Г,т) = е-апт 2/2{ cq°5 (апт + 8)2 [1 - в -(апт+8((Т-т)] । с^0апт апт + 8 (Т - т )е-(апт+5^(Т-т)} = к В уравнении связи (40) переменные Тит расположены «вперемешку». Причем никакими способами невозможно представить зависимую переменную (функцию) т через независимую переменную Т. Таким образом, функцию т = т(Т) нельзя выразить явно. Однако возникшая сложность не может являться большим препятствием для дальнейшего анализа, и эту функцию можно исследовать в таком неявном виде. В математической теории в наиболее общем виде формулируются достаточные условия однозначной разрешимости уравнения Ғ(Т,т) = 0 в некоторой локальной окрестпости рассматриваемой тонки То. В этой же окрестности решается вопрос о существовании производной f ‘(То) неявно заданной функции f (Т). Данное описание результатов исследований в более детальной и точной математической формулировке лежит в основе теоремы о неявной функции, которая является одной из ключевых теорем математического анализа. Теорема существования и дифференцируемости неявной функции. Пусть выполнены условия: • функция Ғ(Т,т) и ее частные производные Ғ)(Т,т) и Ғ^(Т,т) непрерывны в некотором прямоугольнике с центром в точке (То,то) • в точке (То, то) имеет мест о равенство Ғ (То, то) = 0, в то время как частная производная Ғ'Т (То, то) = 0. Тогда справедливы следующие утверсисдения: • уравнение Ғ(Т,т) = 0 определяет единственную непрерывную и дифференцируемую функцию т = f (Т). которая в точке То удовлетвори:т равенству то = f (То): • для всех значений Т, лежащих в некоторой окрестности точки То, имеет место піождстпво Ғ(Т,f (Т)) = 0: f ‘(То) Ғ) (То, то) ҒТ(То, то) ■ Геометрически сформулированная выше теорема означает, что в окрестности точки (То, то) гладкая кривая Ғ(Т,т) = 0 представляет собой график непрерывной дифференцируемой функции т = f (Т). Следует обратить внимание на важную роль, которую играют в математике теоремы существования и единственности. Многие теоретические и практические задачи начинаются с решения вопросов существования и единственности. Это отмечается в таких строгих математических дисциплинах, как математический анализ, дифференциальные уравнения, уравнения в частных производных, теория оптимизации и т. д. Расширим непрерывным образом множество допустимых значений неявно заданной уравнением связи (40) функции с т > 0 на т > 0. Определим величину Т при т = 0. В данном случае мы можем явно выписать формулу для вычисления То: ^=- ^(1 - )• Заметим, что при Т > То экономически оправдано разрабатывать рассматриваемое месторождение оптимальным способом, а при Т< То любая допустимая стратегия разработки газового месторождения приводит к отрицательному значению прибыли, поэтому теряется смысл его разрабатывать. Формулу (41) можно также получить другим способом из определения функционала (9), множества всех управлений, описанных формулой (12), без использования сопряженной переменной. Каждому управлению соответствует свой параметр т. Дополнительно воспользуемся соотношениями (1) - (8), (27), (28). Через I(т) обозначим функционал (9): I(т)= / [cQ(t)-fcn(t)\ exp(-St) dt = / [cq(t)nt-kn] exp(-St) dt+пт / cq(t) exp(-St) dt = T I [cq0 exp(— о ant2 )nt — kn\ exp(—8t) dt + cq°n f T I т exp[anT(t/2 — t) — 8t\ dt. Продифференцируем функцию I(т). В результате получаем I ‘(т) = —kn exp(—8т) + cq0n т exp[anT(t/2 — t) — 8t\} dt = = —knexp(—8т)+cq0n / exp[anT(t/2 — t) — 8t\ dt+cq°n I т ——{exp[anT(t/2 — t) — 8t\} dt = J т OT = —kn exp(—8т) + cq0n exp(anT2/2) anT + 8 {exp[—(anT + 8)t\ — exp[—(anT + 8)T\}+ +cq0n--------—т exp(-----){[(anT+8)(T—т) + 1\ exp[—(anT+8)T\ — exp[—(anT+8)t\}. (43) (anT + 8)2 2 Для разработки месторождения в рассматриваемой модели необходимо выполнение строгого неравенства I‘(т) > 0 при т = 0. Воспользовавшись (43), мы приходим к следующему соотношению: —kn + {1 — exp(—8T)} > 0. Отсюда следует, что неравенство (44) выполняется при всех значениях T > T0, где T0 определяется согласно формуле (41). Заметим, что нам нет острой необходимости полностью рассчитывать громоздкое выражение для производной I‘(т), поскольку требуется только I‘(т = 0). В выражении (43) используется определенный интеграл /^0 IT{т exp[anT(t/2 — t) — 8t\} dt. При т = 0 его можно упростить до следующего выражения: 1 — exp(—8T) I — {т exp[anT(t/2 — t) — 8t\}dt = / ——{exp[anT(t/2 — t) — 8t\} dt = т=0 dT т=0 dT На рис. 2 представлен график неявной функции, заданный уравнением связи (40) при т > 0 и изображенный на плоскости Tt. На графике выделены три ключевые точки, играющие важную роль при построении графика и влияющие на его структуру и поведение. Первая ключевая точка имеет на плоскости координаты (T0; 0), где T0 вычисляется по формуле (41). Для определения второй ключевой точки проведем некоторые математические преобразования. Выделим два отдельных слагаемых в выражении средней части двойного равенства (40): 0Др-аит2/2 0 -апт2/2 ^(T, т) = ---—- + ----— [anT(anT + 8)(T — т) — 8\е-(апт+8)(T-т) = k. (45) (anT + 8)2 (anT + 8)2 Пусть ті является решением следующего уравнения: cq 8 р-д-пт2/2 = k (anT + 8)2 При условии ^j- > k уравнение (46) имеет единственное положительное решение, поскольку левая часть уравнения является убывающей функцией от величины т, и при т ^ то данная функция стремится к нулю. С учетом равенства (45) из (46) следует [anT(anT + 8)(T — т) — 8\е (апт+5)(T т) = 0. Рис. 2. График неявно заданной функции т(Т) Из соотношения (47) вытекает два решения: одно решение получается при Т ^ то и не может быть представлено на плоскости в виде отдельной точки; другое решение задается формулой Ті = ті + апті(апті + 6) Вторая ключевая точка имеет на рис. 2 координаты (Ті;ті), где величина Ті вычисляется по формуле (48), а значение ті определяется из решения уравнения (46). Производная неявной функции т(Т), заданной с помощью уравнения связи р(Т,т) = к, вычисляется по формуле т ‘(Т) р'т(Т,т) Рт (Т,т ) ‘ Вычислим частную производную функции р(Т, т) по переменной Т: рТ(Т,т) = с90[1 - апт(апт + 5)]е-(“пт+5)(т-т)-“пт2/2. Выше было показано, что частная производная рТ(Т, т) < 0 при всех допустимых значениях т и Т. Воспользовавшись неотрицательными значениями координат первой и второй ключевой точки, покажем положительность производной неявной функции т(Т) в точках Т0 11 Ті. Действптелыю: .0) = _рТ(Т0, 0) рТ(Т0,0) с9° е—т0 -рТ (Т0,0) > 0; ‘(Т\ _ рТ(Ті,ті) т (Ті) = — рруТ^ сд°апті е—(аПті+5)(Т1-ті)—апт2/2 > 0 _рТ (Ті,ті)(апті + 6) В третьей ключевой точке производная т‘(Т2) = 0. Воспользовавшись формулами (49) и (50), получим следующее соотношение: Т2 = т2 + апт2 Подставим полученную зависимость (53) в равенство (40): / х С90 ^ = . + 5)2е “т т2 2 [5 + опт.е -1- § “ 2 ] = к. Докажем единственность полученного неравенства 4S- > к. Рассмотрим функцию уравнения при условии выполнения строгого cq° *) = (опт + 5)2 е “Тт 2 2 [5 + опте — “Тт I . Данная функция обладает следующими свойствами: ф(0) = ^- > к и limT-^ = 0. Докажем, что эта функция убывает. Продифференцируем функцию (55) по аргументу т: cq° _тт2С_ - § Ф (т) = —-------—е 2 “тт {|5 + 2о5пт — 2а5пте + «тт ] — v ’ т(апт + 5)3 —а5пт (5т + апт2)е1+ «тт — о3п3т4 — о?5п?т3 — а^п^т 2}. (56) Если выражение в квадратных скобках правой части равенства (56) принимает отрицательные значения, то функция ф(т) строго убывает. Для доказательства преобразуем данное выражение: S 8 апт “пт+5 . 5 + 2о5пт — 2о5пте1+“тт = [о5пт(2 — е «тт)] + [52 — 5(апт + 5)----ДДе “тт ]. Заметим, что о5пт(2 — е1+«тт) < 0 и а“"+5е «т^ > 1. Значит, выражение (57) принимает отрицательные значения. Следовательно, уравнение (54) имеет единственное положительное решение и оно равно т.. Числовое значение величины т. мы можем определить, используя широко известный численный метод деления отрезка пополам. Основой для применения этого метода являются полученные свойства функции (55). Таким образом, при т < т. существует, по крайней мере, одно значение Т, при котором прямая задача имеет решение. В противном случае величине т не соответствует ни одно значение Т. Значит, т. определяет множество всех оптимальных значений т. Из положительности единственного решения уравнения (54) и существования точки (Т 0;0). удовлетворяющей уравнению св язи (41). вытекает. что в точке Т. неявно заданная функция т(Т) достигает своего максимального значения. Можно формально подойти к определению локального максимума неявно заданной функции в точке Т.. Для этого достаточно еще раз продифференцировать производную (49) и убедиться, что в точке Т. вторая производная функции т(Т) отрицательна. Из однозначности неявно заданной функции т(Т) при всех допустимых значениях Т > Т0, единственности локального максимума в точке Т., выполнения строгих неравенств (51) и (52) в точках Т0 и Ті вытекает следующее поведение этой функции, график которой изображен на рис. 2. Начиная с точки Т0 до точки Т. график функции т(Т), пересекая ось т = т1, строго возрастает. Далее он достигает в точке Т. своего максимума и затем при Т ^ то строго монотонно убывает, асимптотинсскн стремясь сверху к оси т = ті. Положительный квадрант плоскости, на котором изображен график функции т(Т), разбит параллельными осями т = ті и т = т. на три части. Из графика функции т(Т) следует, что: • если зависимая переменная т Е (0,тД то имеется взаимно однозначное соответствие между переменными т и Т; в этом случае переменная Т Е (Т0,Ті]; • если зависимая переменная т Е (ту, т2), то одной величине т соответствуют два значения Т. одно из которых больше Т2 . а. другое? меньше Т2. но б(>.тьше Ту в этой области с увеличением величины т уменьшается разность между двумя соответствующими 'значениями Т: • если зависимая переменная т = Т2, то данной величине т соответствует только одно 'значение Т2. мы наблюдаем вырожденный с.тучай предыдущего пункта: в точке Т2 функция т(Т) достигает своего максимума; • если зависимая переменная т > т2, то данной величине т не соответствует ни одно значение Т . Из вышесказанного вытекает, что множество всех т ограничено величиной т2, которое определяется из единственного решения уравнения (54). Напомним, что единственность уравнения (54) наступает при условии выполнения строгого неравенства -J- > к. Значение ту определяется из решения уравнения (46). Данное решение единственно. Далее приведем алгоритм определения всех значений Т, соответствующих заранее заданной величине т = т* > 0. Предполагаем, что исходные данные удовлетворяют строгому со° неравенству -J- > к. Блок 1. Рассмотрим вспомогательную функцию (39), график которой схематично изображен на рис. 1. Подставим в формулу для описания вспомогательной функции (39) вместо значения т величину т*. В этом случае вспомогательная функция (39) имеет следующий вид: /(Т) = 1 - е-(апт*+S)(T-т*) + апт*(апт* + 5)(Т - т*)е-(“пт*+5)(т-т*)/5.(58) Вычислим значения вспомогательной функции (58) в точках, величины которых расположены в порядке возрастания Т = т*,Т Г, = т* + апт*(^пт„^ и Т = Т2 = т* + ^^: / (т *) = 0;(59) /(Ту) = /(т* +---- 5 , ) = 1;(60) апт *(апт * + 5) ** /(Т2) = /(т* + ^*) = 1 - е-+ (апт* + 5)е--ппт+-/5.(61) В соответствии с формулой (38) определим положительное числовое значение s при т = т *: к(апт* + 5)2-пт*2 S cq°5 е . Преобразуем равенство (37) при т = т*. В результате с учетом (62) получаем 1 - е-(«»т*+)(т-т*) + апт*(апт* + 5)(Т - т*)е-(апт*+5)(тт*)/5 = s.(63) Подставим (58) в (63), приходим к уравнению с одним неизвестным: / (Т) = s.(64) Если выполнено нестрогое неравенство s < 1,(65) то переходим к блоку 2. В противном случае переходим к блоку 3. Блок 2. В этом случае параметр s удовлетворяет следующему неравенству: 0 < s < 1. (66) Восполвзуемся равенствами (59, (60) и (64). В резулвтате получаем /(т*) < /(Т) < /(Ті) = /(т* +---- 5 , ). (67) апт *(апт * + 5) Функция J(Т) на отрезке [т*, Ті] является строго возрастающей функцией. Поэтому для численного поиска единственного решения уравнения (67) используем метод деления отрезка пополам. Конец алгоритма. Блок 3. Если выполнено неравенство s > /(Т2) то переходим к блоку 4. В этом случае числовое значение параметра s лежит внутри промежутка от 1 до /(Т2), т.е. 1 < s < J(Т2), или с учетом (64) получаем 1 < /(Т) < /(Тз). Функция /(Т) строго возрастает от Ті д о Т2 и строго у бывает при Т > Т2. Справедливо выполнение верхнего предела Іітт-^ /(Т) = 1. Значит, существует такое значение Ту > Т2, при котором выполняется строгое неравенство s > /(Ту). Следовательно, уравнение (64) имеет два корня. Один корень расположен в промежутке от Ті до Т2, другой корень - от Т2 до Ту. Для получения числовых значений этих корней используем дважды метод деления отрезка пополам. Конец алгоритма. Блок 4. Если выполнено равенство s = /(Т2) то уравнение (64) имеет единственное решение Т = Т2. В противном случае уравнение (64) не имеет решений. Конец алгоритма. Далее мы исследуем поведение точной верхней грани т2 в зависимости от величины параметра к. Напомним, параметр к определяет величину стоимости строительства одной скважины. Для этого продифференцируем равенство (54) по параметру к. В результате получаем т2(к) = "ТГД. <68> VW Выше при вычислении производной функции у в (56) было показано, что производная отрицательна. Значит, с ростом величины параметра к до величины 22- точная верхняя грань т2 строго убывает, и она. стремится к нулю. С уменьшением величины параметра, к до нуля точная верхняя грань т2 строго возрастает, и она стремится к бесконечности. Заключительная часть данного параграфа относится к выявлению максимального значения функционала, определенного на. некотором множестве оптимальных стратегий разработки газового месторождения. Пусть Т’ и Т2 обозначают две точки, расположенные строго по порядку, и пусть выполняется равенство т = т (Ті )= т (Т2).(69) Выпишем два. функционала: 11 = J [cq(t)пt — кп] exp(—5t) dt + пт / cq(t) exp(—5t) dt;(70) /• t t1,-T2 12 = [cq(t)пt — кп] exp(—5t) dt + пт / cq(t) exp(—5t) dt + пт / cq(t) exp(—5t) dt = J 0 Jt Tt^ r T = 12 = 11 + пт cq(t) exp(—5t) dt > 11. J т’ Таким образом, наибольшее значение функционал принимает при большем горизонте планирования. Другая задача состоит в поиске такой пары (Т, т), которая обеспечивает максимальное значение функционала. С учетом (1) - (3) и (12) переписываем интеграл (9) I(Т,т) = f [cQ(t) —kn(t)] exp(—5t) dt = f [cq(t)nt—кп] exp(—dt) dt+пт f cq(t) exp(—5t) dt = J 0 0 t IT[cq° exp( — 0 2 )nt — кп] exp(—dt) dt + cq^nTexp( — ant2 2 'L' exp[—апт (t — т) — St] dt. Вычислим частную производную функции I(Т,т) по переменной т и приравняем ее к нулю. В результате получаем уравнение (40). Уравнение (40) определяет неявно заданную функцию т(Т). С учетом неявно заданной функции т(Т) и равенства (40) продифферен-тіирусм I(Т,т (Т)) по Т: I ‘(Т,т (Т)) = cq° exp{—апт 2(Т)/2 — апт (Т )[Т — т (Т)] — 5Т }пт (Т). (73) Для любого конечного Т правая часть равенства (73) положительна и limy I‘(Т,т(Т)) = 0. Максимальное значение функционал принимает при Т. стремящемся к бесконечности. В этом случае величина т однозначно определяется из решения уравнения (46). Можно другим способом отыскать величину Т, при котором достигается максимальное значение функционала. Для этого вместо задачи 1 с фиксированным временем решить задачу 1 с нефиксированным временем. В этом случае гамильтониан (13) в конечной точке оптимальной траектории с учетом условий трансверсальности (18) и п(Т) = 0 необходимо приравнять к нулю: Н(q(Т), N(Т), п(Т), ^(Т), ф(Т)) = cq(T)N(Т) — кп(Т) — ^(Т)aq(Т)N(т) + ф(Т)П(Т) = = cq°exp[— апт2 — апт (Т — т )]пт = 0. Отсюда следует, что оптимальное значение Т для задачи 1 с нефиксированным временем равно бесконечности. Величину т мы находим из решения уравнения (46). Данное решение единственно.
3. Заключение В настоящей статье мы рассматриваем непрерывную динамическую модель газового месторождения. В рамках модели выписывается функционал для расчета накопленной прибыли. Ставится задача максимизации накопленной прибыли с использованием двух дифференциальных уравнений и двойном ограничении на управление. Данная прикладная задача является задачей оптимального управления с фиксированным горизонтом планирования и со свободным правым концом. Показываем, что оптимальное решение рассматриваемой задачи существует. Для поиска решения используется принцип максимума Понтрягина. Оптимальное решение прямой поставленной задачи состоит в следующем. Весь горизонт планирования разбивается на две части: на первом этапе месторождение разрабатывается с максимальным постоянным темпом бурения скважин, на втором этапе бурение прекращается. Доказывается единственность такого управления. Другая обратная задача сводится к следующему. Пусть фиксирован временной период этапа бурения скважин. Решается прямая задача на максимум. При каких горизонтах планирования фиксированный временной период этапа бурения является оптимальным? Таких горизонтов планирования может быть один, два или вообще их не быть. Исследование проводится на двух рисунках. На каждом рисунке строится график. Каждый график подвергается всестороннему анализу. Для исследования используется теорема существования и дифференцируемости неявной функции. Доказывается, что для случая двух горизонтов планирования наибольшее значение функционала достигается при большей величине горизонта. Для фиксированного временного периода этапа бурения приводится алгоритм численного поиска горизонтов планирования. Доказывается, что при решении прямой задачи с нефиксированным временем наибольшее значение функционал достигает при бесконечном горизонте. В этом случае временной период этапа бурения определяется соответствующей формулой.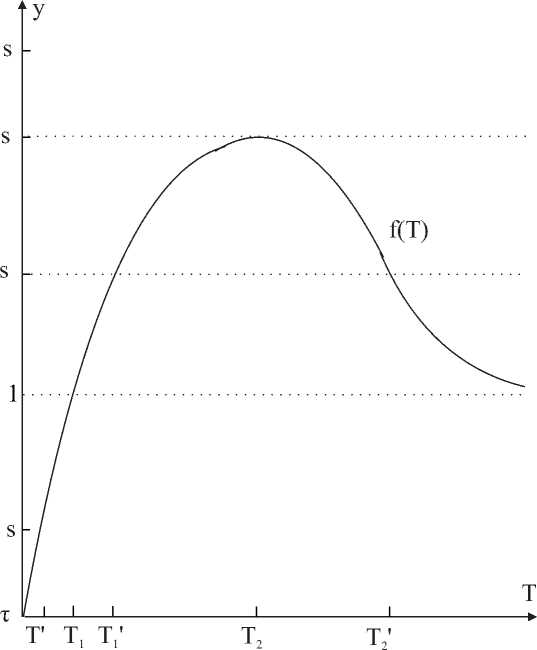
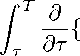
Список литературы Постановка и исследование динамических задач в модели разработки газового месторождения
- Вяхирев Р.И., Коротаев Ю.П., Кабанов Н.И. Теория и опыт добычи газа. Москва: Недра, 1998.
- Закиров С.Н., Лапук Б.Б. Проектирование а разработка газовых месторождений. Москва: Недра, 1974.
- Skiba А.К. Maximization of the Accumulated Extraction in a Gas Fields Model // In: Evtushenko Y., Jacimovic M., Khachav M., Kochetov Y., Malkova V., Posvpkin M. (eds), Int. Conf. on Optimization and Applications (OPTIMA 2018) // Communications in Computer and Information Science, Springer. 2019. V. 974. P. 453-469.
- Хачатуров В.P., Соломатин A.H., Злотов A.В. и др. Планирование и проектирование освоения нефтегазодобывающих регионов и месторождений: Математические модели, методы, применение / под ред. В.Р. Хачатурова. Москва: УРСС: Ленанд, 2015.
- Маргулов Р.Д., Хачатуров В.Р., Федосеев А.В. Системный анализ в перспективном планировании добычи газа. Москва: Недра, 1992.
- Skiba А.К. Dvnamic model analvsis of gas deposit developments // 2018 Eleventh International Conférence Management Of Large-Scale System Development (MLSD). IEEE Conférence Publications, IEEE Xplore Digital Librarv. P. 619-622.
- Скиба, A.К. Поиск в модели газовых место рождений максимальной длины их общей «полки» // Труды МФТИ. 2019. Т. 11, № 2. С. 49-61.
- Эрроу К. Применение теории управления к экономическому росту // Матем. экономика. Москва: Мир, 1974. С. 7-45.
- Ли Э.Б., Маркус Л. Основы теории оптимального управления. Москва: Наука, 1972.
- Понтрягин Л. С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. Москва: Наука, 1976.
- Моисеев Н.Н. Элементы теории оптимальных систем. Москва: Наука, 1975.
- Скиба А.К., Соломатин А.Н., Хачатуров В.Р. Себестоимость добычи в модели газового месторождения: исследование и применение // Труды МФТИ. 2018. Т. 10, № 3. С. 45-53.


