Постановка задачи оптимального захода на посадку беспилотного летательного аппарата с изменяемой в полете структурой
Автор: Пантилеев Андрей Сергеевич
Статья в выпуске: 22 (198), 2010 года.
Бесплатный доступ
Балансирное управление совместно с классическими аэродинамическими органами управления позволит существенно сократить дистанцию посадки. Выводятся уравнения движения с учетом подвижного груза и без него, для беспилотного летательного аппарата с изменяемой в полете структурой
Дифференциальные уравнения движения, изменяемая структура, беспилотный летательный аппарат
Короткий адрес: https://sciup.org/147154714
IDR: 147154714 | УДК: 629.12.053.13
Текст обзорной статьи Постановка задачи оптимального захода на посадку беспилотного летательного аппарата с изменяемой в полете структурой
Математическое моделирование беспилотного летательного аппарата (БПЛА) с изменяемой в полете структурой, позволит на ранних этапах проектирования провести оценку динамики сложной системы. Для этого предлагается провести моделирование движения БПЛА с изменяемой в полете структурой используя дифференциальные уравнения движения летательного аппарата как абсолютно твердого тела [1]. Основное отличие исследуемых уравнений заключается в том, что в них момент инерции не является константой, а зависит от времени.
1. Математическая постановка задачи
Закон изменения момента инерции принимается на основании предложенной в работе [2] схемы изменения структуры (рис. 1).
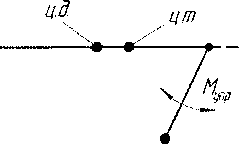
Рис. 1. Схема изменения момента инерции: ц.д. - центр давления, ц.т. - центр тяжести платформы
Представим момент инерции БПЛА с изменяемой в полете структурой следующим выражением, а также его производной
I - = J - + пр^Ь +
,2 ( 2Ь / . . _ . ) ,
+mrpl I — (5Шф + со5ф) + 25Шфсо8ф I, (1)
I, =2л^р/2(—(со8ф-5тф)+(соя2ф-8т2фМ. (2)
С учетом уравнения существования летательного аппарата т = тПП + т^ и соотношения масс груза и платформы km=mmjmTp, собственного момента инерции платформы представленного соотношением J, = ишлрпл2. Здесь и далее рпл -радиус инерции платформы.
С учетом принятых выражений (1) и (2) примут следующий вид:

I. = m ----- —I cos - sin ф) +
+ 2^cos2 ф-sin2 ф^.
Смещение центра тяжести относительно тра масс вдоль осей с учетом принятых выше значений:
цен-обо-
Модели аэродинамических коэффициентов, скоростной напор и угол атаки на основании работы [3], а также безразмерные геометрические параметры представим следующим образом
Сх=Сх0 + У У° +С^-8г, (10)
ЛА
_b + l cosф _ b
I
цм ^+1 ^+1 ^+1
™ =----51Пф.
созф,
Дифференциальное уравнение углового движения dm. L SbA SbY
--- = — to, + C q—--Cvq— dt 7, " mz L y 1, перепишем его с учетом полученных выражений
Су=Су0+С“-а + С^-8е,
Cmz=Cmz0+C“z.« + C^.8e,
Р2 р^+И,2)
2 ’
Vy '.
а = arctan — = arcsin --------
V V
(Н)
d®. dt
^тРил2 +^2 +^ fy (5тф + СО8ф) + 28тфСО8ф кК, +1) С Ьл -С Ьтге,у - + -----СО8ф
Н A — bconstY _ Рпл
Рпл , ’^constYl , ’ Рпл , •
/ bA bA
Учтем в (6), (7), (8) и (9) изменения расстояния между центром давления и центром масс, описанное ранее выражениями (5), а также принятые обозначения (10), (11), (12), (13) и (14). Представим полученную систему дифференциальных уравнений в безразмерном виде относительно перегрузки
\dVx q\ CyQ^-CyOyC>*C>e
--= И--С.А Ч--------h g dt pnX
+ cf'dj-sine + —A ’g
-
1 dPy _ q (, zzSes t ___n ®2^x zi/cx --—\Суо +C a + Cy 8e I—cos0--, (16) g dt ’g
I dtoT q {Cmzo+(^zti+(^8^bA(km+'^
-
8 P^mV+b2+2^b^ sin ф+cos ф)+sin ф созф)
(cy0 + C“a + Cye8e) ^bconstY ^km +1) + b + cos ф)
k-mPm +^2 +2^6 (sin ф + cos ф) + sin ф cos ф)
— = Vx sin0 + Vv cosO, — = УХ cos0 + У, sin0, — = o.. dt x y dt x y di "
Предположим, что движение осуществляется таким образом, что угол атаки остается постоянным и в пределах допустимых (летных значений) или незначительно меняется, тогда без ущерба для достоверности описанного процесса, можно исключить слагаемые в моделях аэродинамики. Также предположим, что скорость движения по глиссаде остается постоянной, тогда скоростной напор можно принять величиной постоянной. Пренебрегая также величинами второго порядка малости, получим на основе (16) следующую систему:
Постановка задачи оптимального захода на посадку беспилотного летательного аппарата с изменяемой в полете структурой
1 dV, q
--- = и-- g di р
-sinO + —' g g dt y
^ = 1ьД g dt p
л'° лХ
®Л cost)--— g
т,0
bcomlY , 6+COS(p bA ЬД^ + V,
к^щ,2 + b2
+ 2(Z>(sin ^- = У, sin 0 + К, cosO, dt у — = К cosO + K sin9, — = ro . dt у dt Система (17) без учета подвижного груза примет следующий вид: 1 dVx g dt 1 , 7 , ^yO xO з рЪе ^У , z-r5e q_ р\ Л?. -smO + ----, g —= —С 0+ —ф§£-cos0-g dt p y p y £ dt PPm , Я ^ / p5e T ^e \ о + _ 7 DconstY1'-'y P Pm V’ = Vx sin 9+ Vv cos0, dt xy — = И cos 9 +И sin 0, — = (o_. dt ydt “ g 8,- 2. Схема посадки Из горизонтального полета, обозначенного на схеме (рис. 2.) точками 12, происходит переход в снижение. Так же как и в классическом варианте, как уже было сказано выше, во время горизонтального полета самолет переводится в посадочную конфигурацию, если это необходимо выпускаются закрылки, подбирается необходимая для посадки тяга двигателя. Следующий этап представляет собой криволинейное движение по дуге окружности 2-3 с радиусом А-2 для входа в глиссаду 3-4. Её угол должен быть как можно больше, потому как именно на этом этапе есть возможность существенно сократить дистанцию посадки. По существу этот этап представляет собой пикирование. Выход из пикирования происходит также по дуге окружности 4-5-6 с радиусом В-5. Затем незначительный прямолинейный участок 6-7 и вновь движение по дуге окружности 7-8-9. Если следовать предложенной схеме, то в районе точки 9 горизонтальная скорость будет незначительной и участок 9-10 может представлять собой практически вертикальную прямую. Рис. 2. Схема полета на заключительном этапе посадки Если умозрительно предположить подобный маневр, то он может быть выполнен следующим образом. Этап полета 2—3—4—5 выполняется при включенном двигателе, осуществлять управление на этом этапе возможно с помощью аэродинамических органов управления (руля высоты, закрылков и элеронов). После прохождения точки 5 движение самолет переходит в набор высоты, при этом вертикальная скорость возрастает от нуля до некоторой величины. Если использовать при наборе высоты только накопленную ранее кинетическую энергию будет проходить интенсивное снижение вертикальной и горизонтальной скорости, этот момент соответствует точке 8. Угол тангажа при этом будет примерно соответствовать углу набора высоты. В виду падения скорости возможен срыв потока на крыле, аэродинамические органы управления в это время не эффективны, но возможно еще использование балансирного способа управления. На заключительном этапе посадки необходимо обеспечить приземление БПЛА с нулевым углом атаки, это возможно путем перемещения центра тяжести. Как уже было сказано ранее основным ресурсом для снижения дистанции посадки является этап 3-4. Чем круче будет пикирование, тем меньше пройденная дистанция. Однако пикирование должно выполняться таким образом, чтобы было возможно выйти из него с последующим набором высоты. Необходимо помнить, что при этом возможна просадка, которая возрастает со скоростью пикирования и как следствие его крутизной. Этап полета 5-6 представлен дугой окружности равной дуге окружности 4-5. Это предположение не совсем верно, так как возможны режимы полета, при котором радиус набора высоты будет меньше, чем радиус выхода из пике. Таким образом, на этом этап полета возможно сокращение дистанции посадки. Радиус дуги окружности дуги 7-8-9 в пределе может быть равным нулю. При этом переход от положительного угла тангажа, соответствующего набору высоты, к нулевому углу тангажа пол- ностью осуществляется с помощью балансирного управления, ввиду того, что скорость полета близка к нулевой и аэродинамические органы управления не работают. Заключение В том случае, если в результате работы будет продемонстрировано, что возможно снижение аппарата с высоты 30 м на дистанции меньше 200 метров, то можно будет сделать вывод о том, что, во-первых, возможно выполнять снижение по глиссаде угол которой больше 4°, а во-вторых, использование балансирного управления на всех этапах снижения, а особенно в заключительном -позволит еще больше Сократить дистанцию посадки. Целесообразно использовать балансирное управление в момент движения около точки 2. При этом если уменьшить статическую устойчивость аппарата, будет возможен более интенсивный разворот, в пределе радиус разворота может быть равен нулю. В процессе пикирования статическую устойчивость желательно не уменьшать, ввиду того, что как было показано в работе Остославско-го, усложнится вывод самолета из пикирования. Ввиду того, что предложена траектория снижения, в качестве критерия оптимизации управления необходимо ввести отклонение действительной траектории от заданной. Итоговый функционал примет вид 4 ^МП^ УЦЦ2+ Хзу 7^ Д J Д (ад (0 - н^2 + х6 (А (0 - r(z))2+ Х7 (8е)2 + х8 (ф)2 U. ~ о1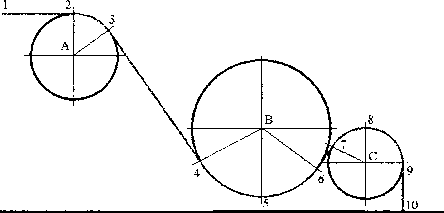
Список литературы Постановка задачи оптимального захода на посадку беспилотного летательного аппарата с изменяемой в полете структурой
- Бюшгенс, Г.С. Динамика самолета. Пространственное движение/Г.С. Бюшгенс, Р.В. Студнев. -М.: Машиностроение, 1983. -320 с.
- Пантилеев, А.С. Задачи исследования динамики движения БПЛА с изменяемой в полете структурой/А.С. Пантилеев//Динамика машин и рабочих процессов: сб. докл. Всерос. науч.-техн. конф., 8-10 декабря 2009 г. -Челябинск: Издательский центр ЮУрГУ, 2009. -С. 138-140.
- AEROSIM BLOCKSET. Version 1.01. User's Guide. -http://www.u-dynamics.com>


