Постановка задачи синтеза квазистационарной стохастической системы

В процессе работы любой системы изменяются значения ее параметров, что приводит к разбросу показателей качества работы системы. Для того, чтобы скомпенсировать влияние случайных факторов без каких-либо дополнительных затрат, нужно решить задачу синтеза корректирующих устройств.

Решение этой задачи осложняется тем, что численные значения некоторых физических параметров изменяются.

Задача синтеза корректирующих устройств квазистационарной стохастической системы может быть сформулирована как задача математического программирования и при определенном выборе коррекции сведена к задаче выпуклого программирования.

1. Описание системы управления

Любая система, имеющая сосредоточенные параметры и, следовательно, представляемая конечным числом дифференциальных и алгебраических уравнений, может быть описана в форме переменных состояния.

Структурная схема системы управления в общем случае приведена на рис. 1. Введены следующие обозначения: X = [xix2...x„]T- вектор состояний системы; Y = Ь^уг—Уи]7- вектор выходных сигналов; U = [щ и2...м„]т - вектор входных (управляющих) сигналов; G = [gj g2—g/]T- вектор возмущений.

В общем случае в матричном виде уравнения состояния системы в пространстве состояний имеют вид:

x = f(x,y,g, Z);

у = h(x, w, 0,                                 (1)

где f и h - вектора нелинейных зависимостей:

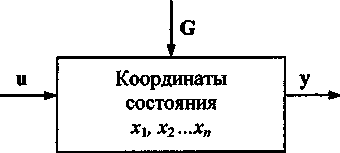
Рис. 1. Схема системы управления

В тех случаях, когда векторные нелинейные зависимости fitigk могут быть линеаризованы (например, путем разложения в ряд Тейлора), они становятся линейными комбинациями переменных состояния х„ входных переменных м_у и возмущений gi. В этом случае уравнения состояния в векторно-матричной записи принимают вид:

x(t) = A(Z)x(0 + В(0п(0 + H(f)g(0;

y(t) = C(/)x(0 + D(/)u(0, (2) где A(t) - собственная параметрическая матрица системы, [пхп], B(t) - входная матрица системы,

[пхт], H(Z) - матрица возмущений, [их/], C(z) - выходная матрица системы, [Ахи], D(f) - выходная матрица, [Ахти].

Любая система, описываемая уравнениями состояния (2) может быть представлена в виде структурной схемы (рис. 2).

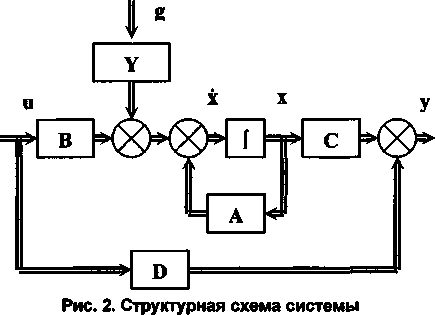
Если элементы матриц А, В, С, D не зависят от времени, то система стационарна, и уравнения в переменных состояния приобретают вид:

х = Ах + Bu + Hg;

y = Cx + Du.                            (3)

Рассмотрим класс линейных стационарных систем управления, движение которых может быть описано системой линейных неоднородных дифференциальных уравнений. Для простоты положим в системе (3) матрицы Н и D нулевыми.

Движение системы в свободном состоянии описывается линейной системой однородных дифференциальных уравнений с постоянными коэффициентами или в векторно-матричной форме:

х = Ах.

Характеристическое уравнение системы:

D(X) = |XE-A| =0.                   (4)

Решение уравнения (4) дает значения корней Х„ / = 1...п, которые позволяют судить о поведении системы в свободном состоянии.

Вывод характеристического уравнения системы в свободном состоянии осуществляется независимо от числа входов и выходов системы, поэтому методика описания системы с помощью пространства состояний является универсальной формой описания поведения систем всех видов: как линейных, так и нелинейных, как односвязных, так и многосвязных.

Если уравнение состояния линейной системы представить в виде

Mx = Ах + Ви, где М = [ш,у5,у] = diag(/Mn, m22-••'”»») - диагональная матрица инерционных коэффициентов системы; 5У - символ Кронекера; А = [а,у] - квадратная матрица размера пхп; В = [6,у] - квадратная матрица размера пхк, х = [х^-.х^ - вектор состояний системы; и = [«!...«„] - вектор входных сигналов, тогда полная система уравнений пространства со стояний стохастической квазистационарной системы управления запишется в виде:

М*х = А*х + В*и;                      . .

У =Сх, где М*,А*,В* - математические ожидания матриц М, А, В, содержащие статистически осред-ненные значения коэффициентов, т.е.

^А* = [ jZOy payday ] = [ay ], /, j = 1,и;

^B‘ = [ ^f^bydby ] = [X \i = Vn,j = 1, k,

M* = [ J/(m„ }m_udm_u ] = diagO^Xa-XrA С - выходная матрица.

• 2.    Система ограничений

Характеристическое уравнение системы (4) в развернутом виде:

D^X^ = Хп + <1\Хп * +... + ип_\Х + ип> причем коэффициенты этого уравнения представляют собой функции от параметров объекта управления:

ai=aj®,i = l,n.                        (6)

Известно, что динамические свойства системы определяются, главным образом, ее полюсами, т.е. корнями характеристического уравнения. Так, необходимым и достаточным условием асимптотической устойчивости линейной системы является нахождение ее полюсов в левой части комплексной плоскости. Характер переходных процессов в системе зависит от взаимного расположения этих полюсов.

Для исходной линейной квазистационарной стохастической системы, описываемой первым уравнением системы (5) желаемое расположение полюсов на комплексной плоскости может быть обеспечено введением модального регулятора, т.е. линейной обратной связи по вектору состояния [1]. Уравнение такой связи можно записать следующим образом:

u = v - Кх.

В этом уравнении v - новое обозначение вектора входных (задающих) воздействий; К - матрица обратной связи. Если u, v - скаляры, то К является матрицей-строкой, элементы которой представляют собой коэффициенты обратных связей по всем составляющим вектора х.

Очевидно, что существование матрицы обратной связи К может быть гарантировано только в том случае, если структура самого объекта не накладывает ограничений на возможность управления состоянием объекта х с помощью входного воздействия и, т.е. объект должен быть полностью управляем.

После введения модального регулятора получаем новую систему, которая описывается уравнением вида:

М*х = А*х + B*(v - Кх) = А*х + B*v - ВКх = = (А* - ВК)х + B*v = Аскх + B*v, где

СК

°п -кх	°12 — ^2 '	" °1л ~
а21	°22     "	"     °2и
_ ^и1	°„2     •	•     Опп

Необходимо определить матрицу коэффициентов обратных связей К, при которой замкнутая с помощью обратной связи по состоянию система имела бы желаемое распределение полюсов, т.е. желаемый характеристический полином D_ti(pY

Z>o(p) = det|pI-ACK|.                       (7)

Раскрывая определитель (7), получим характеристическое уравнение с модальной коррекцией

D^p) = X” + аД”-* +...+ а„_1Х + а„, где коэффициенты этого уравнения

«.“аЛаДЕШСУ^!,")-           (8)

Для создания желаемого характеристического полинома воспользуемся прямым корневым мето дом синтеза.

Желаемый характеристический полином

о*(х)=(х-х1)(х-х^)...(х-х;)=

= X" +^Х”-1 +...+6„_]Х+6„ = 0,            (9)

где X* - желаемые значения корней характеристи ческого полинома.

Приравнивая соответствующие коэффициенты уравнений (8) и (9), получим:

аКГаД^В^^ХГА;.^).         (10)

Совокупность уравнений (10) представляет собой систему ограничений, накладываемых на параметры системы и корректирующих цепей. Эта система может быть как линейной, так и нелинейной. Она всегда нелинейна относительно значений корней желаемого характеристического полинома и может быть линейной и/или нелинейной относительно вектора к в зависимости от вида коррекции.

Пусть т - число параметров корректирующих цепей, а и - порядок системы. Возможны следующие варианты:

• •    если т < п, то задача может не иметь решения;

• •    если т = п, то параметры коррекции определяются однозначно;

• •    если т > п, то возможны несколько решений задачи (т.е. в этом случае система обладает гибкостью по отношению к вектору q, но в этом случае система (10) однозначно будет нелинейной).

Очевидно, что наибольший интерес представляет второй случай, когда число параметров корректирующих цепей совпадает с порядком системы. Такой вариант обеспечивает именно модальная коррекция, при этом достигается линейность системы (10) относительно параметров вектора коррекции к = [А#].

Рассмотрим квазистационарную стохастическую систему, которая в свободном состоянии описывается уравнениями вида где х - и-мерный вектор состояния; А = [а,,] - собственная параметрическая матрица коэффициентов системы. Введем корректирующее устройство описанным выше способом. Уравнение, описывающее систему примет вид:

х = Ах;

А = А-К,

(П)

где К - матрица коэффициентов корректирующих цепей размером [ихи]:

-^ -Х2 о

К =

• А о

о

_ 0    ......

Характеристическое

уравнение системы в

этом случае будет иметь вид

п(х)=|хе-а| = о.

Раскрывая определитель, получаем

D(X) = Xⁿ+c_]X” * +...+с_и_]Х + с_п, где с, = сДь Х₂...Х„).

Так как все коэффициенты kv..k„ находятся в первой строке матрицы А, зависимости с А) будут линейными относительно этих коэффициентов.

Уравнение (10), записанное в матричной фор ме, примет вид

С = В,                                 (12)

где С = [ci с₂...с„]^т, В = \bi Ь₂...Ь^.

Так как элементы [cj линейно зависят от параметров коррекции, то можно записать

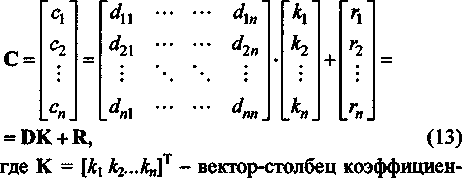
тов корректирующего устройства; D = [dy] - матрица, элементы которой зависят от элементов мат рицы А ; R = [г! r2...r„V - вектор-столбец, элементы которого зависят от элементов матрицы А и не зависят от вектора К; В = [Z>i 62...6„]т - вектор-столбец, элементы которого - функции корней желаемого характеристического полинома.

Уравнение (12) с учетом этого перепишется в виде С = В = DK + R . Обозначая G = В - R, по лучим:

DK = G.                            (14)

Уравнение (14) представляет собой систему ограничений, записанную в матричной форме.

Благодаря введению в качестве корректирующих цепей жестких обратных связей по каждой переменной состояния получаем:

• •    систему ограничений вида (14), линейную относительно вектора параметров К;

• •    однозначное соответствие между корнями желаемого характеристического полинома и параметрами корректирующих цепей.

• 3.    Критерий оптимальности

Так как ряд параметров системы в процессе работы претерпевает случайные изменения (что, в свою очередь, приводит к возникновению случайных изменений динамических свойств системы), задача синтеза имеет статистический характер.

Выберем критерий оптимальности в частотной области. Для этого применим метод определения глобальной чувствительности систем к большим вариациям параметров [2], минимизация которой может быть использована в качестве целевой функции. В основу метода положено однозначное соответствие свойств функции Михайлова качественным показателям свободной составляющей переходного процесса. В качестве критерия оптимальности выберем дисперсию функции Михайлова:

F^Z^O)}, (15) методика получения которой изложена в [2].

Так как коэффициенты корректирующих цепей входят в характеристический полином линейно (из-за использования метода модального управления), выражение для дисперсии функции Михайлова будет представлять собой квадратичную форму относительно этих коэффициентов.

В результате такого выбора критерия оптимальности и метода управления задача синтеза квазистационарной стохастической системы сведена к задаче выпуклого программирования с системой ограничений вида (14) и целевой функцией вида (15).