Постановка задачи структурно-элементного моделирования интерференции струй в блоке

Рассматривая современные работы [5–9] в области изучения протекания процессов газодинамической природы, все чаще можно проследить идею о том, что имеет смысл опираться на вычислительные эксперименты не только как на способ проверить верность теоретических предположений на практике, но и как на новую методологию исследований научного и прикладного характера. В чем на данный момент помогает повсеместное использование компьютерного моделирования процессов движения вязкой жидкости вкупе с огромными базами данных, собранными за предыдущие десятилетия.

Опираясь на определение А. А. Самарского о том, что математическое моделирование несет в своей основе базовую «связку» – «модель-

алгоритм-программа», можно утверждать, что какой бы из трех компонентов технологического цикла не нес в себе гипотетическую ошибку, это, несомненно, скажется на остальных, и что более важно – на результате проведенных вычислений.

Как верно сказано в работе [5], развитие технологии вычислительного эксперимента во многом обязано появлению большого количества вычислительных мощностей на базе персонального компьютера посредством развивающихся сложных систем многопроцессорных вычислений.

Но как бы ни были точны и разнообразны математические и физические модели, нельзя полностью избавиться от экспериментов натурных – это служит веским поводом опираться в разработках не только на данные, полученные в результате расчетов, но и на эмпирические данные, полученные в прошлом.

В наше время задача математического моделирования при разработке новых изделий решается зачастую использованием специализированного прикладного программного обеспечения (далее ППО), что сильно увеличивает скорость получения адекватных расчетных данных для проектирования. А этот параметр является важным фактором для эффективной работы в области газодинамики, по мнению авторов работ [10–13].

С другой стороны, с увеличением вычислительных мощностей и скоростей также растет потребность в проведении этих вычислений и усложняются задачи, ставящиеся перед программным обеспечением инженерных расчетов. В отличие от расчета параметров одиночной сверхзвуковой струи [14–18], проведение вычислений для моделей сложных составных блочных струй уже не является столь тривиальной задачей. С учетом всех газодинамических процессов подобные вычисления могут занимать десятки часов.

Опираясь на вышесказанное, а также на тезисы, представленные в [19], можно утверждать, что структурно-элементный метод (далее СЭМ) позволит получать удовлетворительные данные для проведения проектировочной деятельности и решения ряда специфических задач газодинамики [1–4, 12, 15–18].

В рамках обозначенной проблемы задача по расчету интерференции струй в блоке структурно-элементным методом является приоритетным направлением развития метода.

1.    Блочные составные струи

Блочные сверхзвуковые струи – это газовые струи, истекающие в свободное или затопленное пространство одновременно из нескольких близлежащих сопел – соплового блока. В зависимости от режима течения и компоновки соплового блока блочные струи можно разделить на три вида [10, 18].

В случае если сопла располагаются довольно свободно, возможно истечение отдельных струй без взаимодействия на начальном и основном участках струи. В таком случае эту блочную струю можно рассматривать как несколько отдельных ²⁹⁷ одиночных сверхзвуковых струй. Подобная «свободная» компоновка реализована в отечественной ракете «Протон-М» и представлена на рис. 1.

Также возможен вариант, когда несколько струй взаимодействуют на основном участке. В таком случае происходит объединение спутных струй в один общий поток. Но так как на таких расстояниях уже нет четко выраженной ударноволновой структуры, и струя представлена в основном турбулизированным потоком истекающего газа, то подобное взаимодействие также не несет качественных изменений в сверхзвуковом течении.

Интересующий же нас вариант взаимодействия возникает, когда слияние нескольких струй происходит на газодинамическом участке струи таким образом, что формируется сверхзвуковая состав-

Рис. 1. «Протон-М»

ОСМИЧЕСКИЕ АППАРАТЫ 1Л ТЕХНОЛОГИЯМИ

Том 7

ная струя, характеризующаяся более сложной пространственной ударно-волновой картиной течения. Различные варианты объединенной ударно-волной структуры нескольких пересекающихся на начальном участке струй изображены на рис. 2.

нерасчётности режима течения. Стоит отметить, что для компоновки с четырьмя и более соплами на режимах течения с большой степенью нерас-чётности есть вероятность возникновения сильных обратных токов газа в межсопловое пространство.

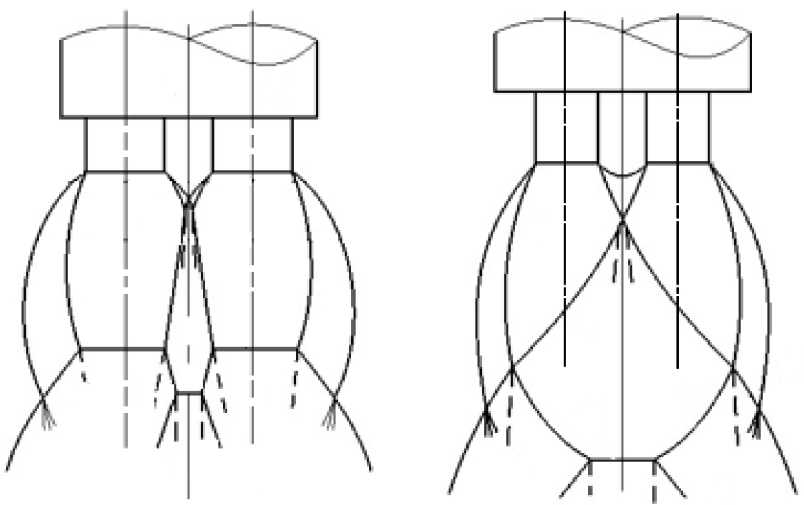
Рис. 2. Структура блочных сверхзвуковых струй

В этом случае увеличивается вероятность возникновения интерференции ударных волн. Существуют различные варианты взаимодействия, например, в работе [13] показано, что в ряде случаев существует опасность формирования обратных течений, которые с точки зрения практического рассмотрения блочных и составных струй применительно к летательным аппаратам [10, 18] могут оказывать как силовое, так и тепловое воздействие на многосопловую конструкцию.

Формирование ударно-волновой структуры сверхзвуковой струи происходит благодаря распространениям малых волн разрежения и сжатия, распространяющихся по струе в процессе ее истечения из сопла [6]. Как известно, в более сжатых слоях газа их распространение происходит с большей скоростью, вследствие чего натекающий на преграду поток будет формировать на небольшом расстоянии перед преградой скачок уплотнения, изменяющий структуру свободно истекающей струи [18]. Такой же механизм верен и для взаимодействия струй друг с другом. Под интерференцией блочных струй в настоящей статье подразумевается изменение ударно-волновой конфигурации каждой из взаимодействующих между собой струй в результате пересечения их течений на начальных участках с возникновением уже общей ударно-волновой структуры – скачков уплотнения, дисков маха и поверхностей разрывов течения и других газодинамических элементов.

Конфигурация скачков уплотнения в объединенных составных струях зависит от таких параметров, как расстояние между соплами и угол между их осями, вынос сопел от общей плоскости, а также большую роль играет коэффициент

В случаях истечения продуктов сгорания с высокой температурой такие токи могут оказывать ощутимое воздействие на элементы конструкции соплового блока. А в случае возникновения на изделиях ракетной техники может вести к скачкам донного давления, влияющим на полетные качества аппарата. Немаловажный эффект интерференции струй в многосопловой компоновке проявляется в усилении акустического воздействия как на летательный аппарат, так и на стартовое сооружение [20–23].

В настоящее время конструктивные схемы многосопловых устройств используются в разных областях техники и технологических процессов. Так, например, основной областью применения многосопловых устройств можно назвать авиационную и ракетно-космическую технику. Подобные компоновки ракетных двигателей повсеместно используются на ракетах-носителях отечественного и иностранного производства. Например, «Ангара-А5» использует для первой ступени компоновку из четырех двигателей, американский «Falcon 9» – сборку из девяти разгонных блоков (изображено на рис. 3). В свое время вариации советской ракеты Р-7 для первой ступени использовали 4 разгонных блока с плотной четырех-сопловой компоновкой РД-107 (рис. 4).

Вследствие распространенности использования блочных струй в ракетной технике неудивительно возникновение потребности в создании метода моделирования структуры и параметров блочных струй, с целью максимизировать точность расчетов для проектирования новых изделий, попадающих под их воздействие. Увеличение скачков уплотнения и их интенсивности в блочных струях ведет к изменению нагрузок на элементы

Рис. 3. Старт «Falcon 9»

Рис. 4. Сопловые блоки ракеты Р-7

конструкции, попадающие в данную струю, а значит, ведет к потребности изменения характеристик тех или иных деталей, поверхностей, покрытий. Также изменение ударно-волновой конфигурации блочных сверхзвуковых струй может вести к изменению формы факела истекающего газа, а значит, есть вероятность попадания в зону воздействия элементов, ранее не рассчитанных на подобное силовое и тепловое воздействие. Между одиночными сверхзвуковыми струями и составными можно провести аналогию, поскольку подобласти течения, на которые струю можно разделить [1, 12, 15], встречаются в обоих случаях. Рассмотрим кратко методы расчета газодинамических процессов.

2.    Методы расчетагазодинамических процессов

В большинстве своем используемое для газодинамических расчетов специализированное расчетное ППО основывается на различных вариациях численных методов моделирования. Для решения различных задач газоструйных течений можно отметить такие численные методы, как:

• 1.    Метод прямого численного моделирования DNS (Direct Numerical Simulation) – на данный момент самый «громоздкий» и требовательный к вычислительным мощностям метод, производящий расчеты с заранее определенной степенью точности для всего расчетного поля течения. В настоящее время практически не используется в «чистом виде», но является основой для других методов конечных элементов.

• 2.    Метод моделирования крупных вихрей LES (Large Eddy Simulation) с дополнениями для решения определенных типов задач, таких как VLES (Very Large Eddy Simulation), MILES (Monotonically

• 3.    Метод моделирования на основе осреднен-ных по Рейнольдсу (Фавру) уравнений Навье-Стокса – RANS (FANS) и URANS (нестационарные RANS). RANS – метод конечных элементов, основанный на использовании расчетных уравнений Навье-Стокса, осредненных по Рейнольдсу (или по Фавру). Один из самых «популярных» методов моделирования сверхзвуковых струй, как одиночных, так и блочных [9, 20], так как наименее требователен к вычислительным мощностям и имеет возможность быть «подогнанным» для решения характерных задач. Несомненно, метод имеет и минусы – система уравнений изначально является незавершенной, что приводит к необходимости введения дополнительных разрешающих соотношений на стадии постановки задачи для расчета.

Integrated LES), DES (Detached Eddy Simulation) [14] и пр. Более ориентированный метод, позволяющий получать параметры турбулентных потоков с различной степенью точности. Можно сказать, что метод является промежуточным между прямым численным моделированием и решением осредненных уравнений Навье-Стокса [8]. Он основан на двух положениях:

– поле скорости можно разделить на движения малых и крупных вихрей, притом расчет крупных можно производить отдельно от мелких;

– возможна аппроксимация взаимодействий между собой этих зон только по крупным вихрям.

Таким образом, мелкомасштабное движение исключается из уравнений Навье-Стокса, что приводит к значительной экономии временных и вычислительных ресурсов для расчета поля течения.

Стоит отметить, что для решения современных задач [7, 24] также используется метод С. К. Годунова, являющийся вариацией метода контрольных объемов и позволяющий рассчиты-

I— ОСМИМЕ АППАРАТЫ II ТЕХНОЛОГИЯМИ вать газодинамические течения с разрывами параметров.

Как несложно догадаться, специализированное ППО, использующее конечно-элементный метод, получило широкое распространение за счет универсальности его использования, а также как инструмент решения задач различной направленности с низким порогом вхождения для пользователя. Но с точки зрения решения газодинамических задач подобный метод имеет ряд проблем, таких как длительность времени расчетов, которая зависит как от сложности ³⁰⁰ конфигурации расчетной области и ее размеров (количество расчетных ячеек), так и от требуемой точности, а также невозможность выделить в потоке скачки уплотнения без графической обработки результатов.

Исходя из вышесказанного, рассмотрим моделирование газоструйных процессов со стороны структурно-элементного метода.

3.    Структурно-элементный метод моделирования газодинамических процессов

СЭМ представляет собой научное направление, сформированное на кафедре А4 Балтийского государственного технического университета «Военмех», описанное в работах [1–4, 15] и развивающееся по сей день [4, 16–18, 25].

Использование ППО, основанного на данном методе, позволяет снизить степень предварительной проработки условий, оставляя лишь ограниченное число переменных, требуемых к определению при постановке задачи.

В соответствии с методологией СЭМ построение решения проводится в несколько этапов.

Первый этап решения задачи методом СЭМ – разработка физической модели исследуемого процесса. На данном этапе выделяются и изучаются факторы, оказывающие существенное влияние на процесс формирования структуры течения. Априорной информации в большинстве случаев достаточно, в противном случае на данном этапе привлекаются физические и вычислительные эксперименты, а в ряде случаев требуется постановка экспериментов, не проводившихся ранее, для установления взаимовлияния выявляемых факторов на структуру течения.

Физическая модель принимается, если она [1, 12]:

• 1)    позволяет разбить поле течения на подобласти однородных процессов, для которых разработаны базовые физико-математические модели;

• 2)    позволяет определить, какие физикоматематические модели необходимо разработать дополнительно для описания процесса в исследуемой задаче;

Том 7

• 3)    дает возможность определить вид функций для аппроксимации формы границ подобластей и распределений параметров течения внутри этих подобластей.

Эти подобласти совместно с границами образуют структурную сетку, разбивающую все поле течения на макроячейки, внутри которых исследуемые параметры изменяются монотонно [1, 12].

Второй этап решения задачи методом СЭМ начинается с разработки перечня математических моделей, позволяющих описать исследуемый процесс. Совокупность математических моделей представляет собой разрешающую систему расчетных соотношений, достаточную для определения форм и размеров макроячеек структурной сетки и ключевых параметров потока в любой точке поля течения.

Универсальность метода СЭМ применительно к решению задач стартовой газодинамики достигается блочной структурой при построении решения. Элементами блочной структуры являются типовые модели течения. В рамках метода СЭМ к настоящему моменту времени разработано большое число типовых моделей, приведенных, например, в [12]. Такие модели, согласно концепции метода, относятся к базовым.

Каждому структурному элементу соответствует своя базовая физико-математическая модель. Набор базовых моделей позволяет описать течение в рассматриваемой задаче. Часть из этих моделей принимается по разработанным ранее задачам, если структурные элементы по условиям новой задачи повторяют структурные элементы из уже решенных задач. Другая часть моделей разрабатывается соответственно перечню, составленному на начальном этапе физического описания исследуемого процесса. Какие-то модели могут быть дополнены, если того требуют условия задачи.

В разработке комплекса базовых физикоматематических моделей типовых процессов, описывающих границы структурных элементов и распределение параметров внутри подобластей течения, заключается основная научная новизна структурно-элементного метода.

К типовым можно отнести процессы, результатом которых становятся важные структурные элементы модели: косые скачки уплотнения постоянной и переменной интенсивности, прямые скачки (диски Маха), пусковые ударные волны, изоэнтропические течения, слабые возмущения, нерегулярные отражения ударных волн от различных преград в плоском и осесимметричном случае [25]. Такие структурные элементы зачастую рассматриваются как самостоятельные задачи и могут представлять отдельный интерес для изучения. Например, в работах [13, 23] подробно рассматриваются вопросы возникновения и взаимодействия ударных волн как между собой, так и с различными элементами конструкции. Использование и учет основных положений таких работ при разработке базовых моделей допускаются в рамках методологии СЭМ. Поскольку математические модели разрабатываются фактически в фундаментальном аспекте, они могут использоваться при решении разнообразных задач стартовой газодинамики. Поэтому применение комплекса базовых моделей от задачи к задаче обеспечивает универсальность метода СЭМ.

нию с количеством узлов сеток конечно-объемных методов определяет скорость алгоритмов СЭМ.

На заключительном этапе решения задачи проверяется достоверность получаемых результатов обязательной проверкой их адекватности по статистическим критериям. В качестве такого может применяться, например, критерий Фишера в заданном диапазоне варьирования исходными данными [2].

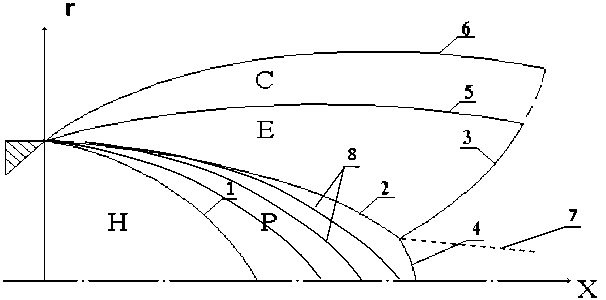
Рис. 5. Структурная сетка неизобарической турбулентной струи в пределах первой ударно-волновой конфигурации: 1 – первая характеристика; 2 – падающий скачок уплотнения; 3 – отраженный скачок уплотнения; 4 – диск Маха; 5 – внутренняя граница слоя смешения; 6 – турбулентная граница струи; 7 – линия тангенциального разрыва; 8 – характеристики волны разрежения; Н – подобласть невозмущенного изоэнтропического течения; Р – подобласть изоэнтропического расширения; Е – подобласть изоэнергетической части сжатого слоя; С – подобласть смешения истекающих газов с окружающей средой

В качестве примера разбиения поля течения на подобласти структурных элементов на рис. 5 приведена структурная сетка первой ударноволновой конфигурации (УВК) стационарной не-дорасширенной струи.

Подобласть невозмущенного изоэнтропического истечения от подобласти изоэнтропического расширения газа отделяет первая характеристика. Косой висячий скачок отделяет подобласть P от подобласти Е и служит границей изоэнергети-ческой подобласти сжатого слоя [1].

Далее по потоку отраженный скачок уплотнения 3 ограничивает сжатый слой. При возникновении нерегулярного отражения висячего скачка уплотнения 4 подобласть Р замыкается диском Маха.

Слой смешения С заключен между внутренней границей 5 и внешней границей 6, представляющей собой турбулентную границу струи. Отраженный скачок в слое смешения вырождается и совместно с границами 5 и 6 замыкает подобласть смешения справа. Геометрия структурных сеток для нестационарных задач становится зависимой от времени.

Даже при относительно большом числе структурных элементов система расчетных соотношений значительно меньше, чем в случае решения аналогичной задачи конечно-объемными методами. Малое число узлов интерполяции по сравне-

Заключение

В настоящий момент разработаны базовые модели для использования СЭМ как инструмента моделирования и расчета течений одиночных струй. Успешное решение задачи по расчету стационарной неизобарической одиночной свободной струи [2, 4] и нестационарной неизобарической струи при выходе ДУ на режим работы с помощью метода СЭМ открывает возможность решения задачи по расчету блочных составных струй как одиночных струй, взаимодействующих друг с другом.

Поскольку взаимодействие рассматриваемых составных струй происходит в пределах первой УВК, то для достижения поставленной задачи необходимо разработать ряд новых моделей, которые впоследствии могут быть взяты в качестве базовых:

• 1)    уточненная модель границы струи, учитывающая процессы в межсопловом пространстве (при многосопловой компоновке донное давление является неравномерной величиной);

• 2)    модель математического расчета области изоэнтропического течения с учетом волн разряжения (области Н, Р, рис. 5);

• 3)    уточненная модель нерегулярного отражения скачка уплотнения (поскольку при подобном взаимодействии струй растет интенсивность скачков уплотнения, что приводит к учащению нере-

• I — ОСМИМЕ АППАРАТЫ VI ТЕХНОЛОГИЯМИ

Том 7

гулярности отражения – с образованием прямых скачков уплотнения, рис. 2).

Разработка новых и уточнение существующих базовых моделей метода будет закономерным развитием структурно-элементного моделирования и как предмета научного интереса (ввиду того, что большинство базовых моделей одиночных струйных течений в том или ином виде транслируются в более сложные модели газодинамических процессов и структуру блочных струй), и как метода для специализированного расчетного ППО, призванного в кратчайшие сроки предоставлять интересуемые параметры рассчитываемого потока, его воздействия на помещенные в него объекты и визуализацию картины течения, увеличивая тем самым темпы расчётной и конструкторской деятельности.