Постобработка СЗМ-изображений решением обратных задач

При проведении исследований топологии поверхности с использованием сканирующих зондовых микроскопов могут возникать различные по физической природе и форме явления, искажающие топологию поверхности. В данной работе проводится исследование различных факторов, вносящих искажения, и указываются способы их устранения.

Проблему влияния искажений можно решить несколькими путями.

• 1.    Изменять конструкцию отдельных узлов сканирующего зондового микроскопа, повышая точность измерений, и минимизировать влияние помех аппаратными средствами.

• 2.    Производить обработку измерительного сигнала, повышая соотношение сигнал—шум.

Первый путь решения проблемы связан с дорогостоящей научно-исследовательской работой и большими затратами на производство новых узлов. Второй метод позволяет с меньшими затратами улучшить результаты измерений на существующем оборудовании. Обработку сигналов можно производить при помощи аналоговых методов и соответствующих устройств. Альтернативой аналоговым методам являются цифровые методы обработки сигналов. Цифровые методы обладают более богатым разнообразием алгоритмов и возможностей. Кроме того, цифровые методы позволяют производить обработку не только в процессе измерения, но и после эксперимента — постобработка. Цифровые методы также обладают возможностью простого изменения параметров алгоритма обработки сигналов и самого алгоритма автоматического управления сканером при малых временных и материальных затратах по сравнению с аналоговыми методами. При использовании аналоговых методов обработки сигналов изменение параметров алгоритмов управления и алгоритмов обработки сигналов сопряжено с изменением принципиальной электрической схемы. С помощью цифровых методов возможно проще добиться более высокой точности по причине отсутствия влияния таких факторов, как температурный дрейф и других внешних шумов.

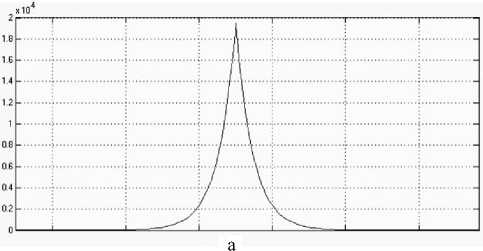
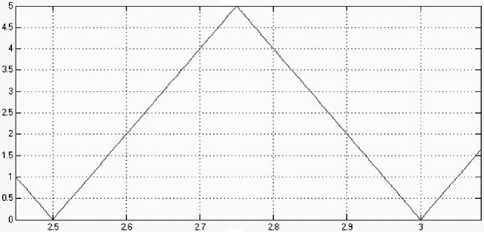
б

Рис. 1. Искажение треугольной структуры.

a — искаженный сигнал, б — исходный сигнал

Задача работы была сформулирована следующим образом.

• 1.    Оценить (по возможности, количественно) искажения в результате решения прямой задачи в управлении сканером с учетом действия шумов и помех.

• 2.    Наметить пути и разработать алгоритмы решения обратной задачи, в том числе с учетом параметров шумов и помех.

• 3.    Разработать программное обеспечение для решения обратной задачи.

• 4.    Провести количественную оценку результатов решения обратной задачи с помощью разработанных алгоритмов и программ.

При анализе помех и результатов обработки сигналов мы будем использовать критерий — близость формы сигнала по значениям невязки

5( x) = g (x) - w (x), где δ(x) — величина невязки; g(x) — измененный сигнал; w(x) — изначальный сигнал.

Анализ искажения будет проводиться в два этапа:

• 1)    выявить основные эффекты, вносящие искажения, и описать математически эти искажения, т. е. решить прямую задачу;

• 2)    решить математически обратную задачу, из чего получим алгоритм обработки изображения.

Разберем основные эффекты, вносящие искажения. Рассмотрим все эффекты на примере двухмерного случая — профилей поверхностей, получаемых при проходе зонда.

ТУННЕЛЬНЫЙ ЭФФЕКТ

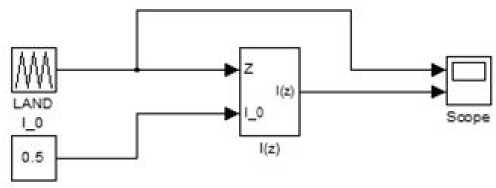
Рис. 2. Модель искажений, вносимых туннельным эффектом.

(Используемые элементы пакета моделирования: "Repeating Sequence", "Constant", "Scope", "Subsystem")

Туннельный эффект описывается формулой (1)

Г f l — f 2 f z пр ⁽ x ) = I 0 ^k e I ² ^

z ( x ),

где z _пр ( x ) — искаженный профиль поверхности; I ₀ — опорный ток; k — коэффициент соответствия тока и расстояния; f ₁ , f ₂ — работа выхода материала зонда и исследуемого образца; z ( x ) — исходный профиль поверхности [1].

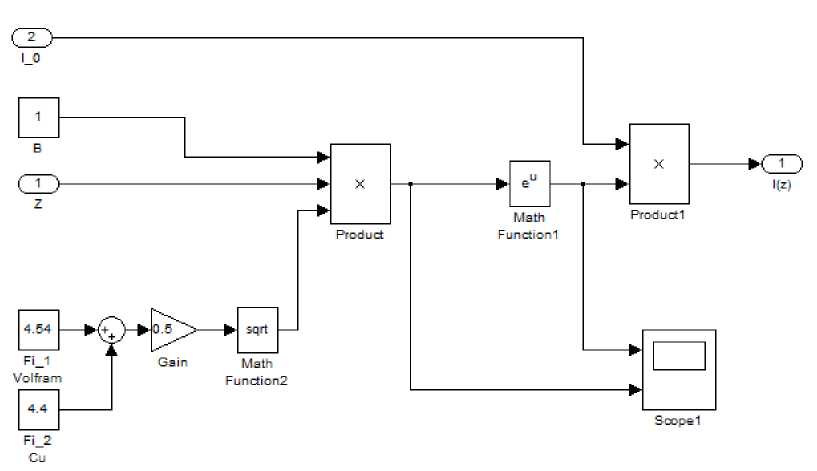
Рис. 3 . Модель туннельного эффекта.

Используемые элементы пакета моделирования: "Add", "Gain", "Math Function", "Product", "In", "Out", "Constant", "Scope", "Subsystem")

Данный эффект проявляется на плавно возрастающем профиле, например треугольной формы. Искаженный сигнал представлен на верхнем графике (рис. 1, а), а изначальный сигнал на нижнем (рис. 1, б). Моделирование произведено с помощью программного пакета MatLab Simulink.

Модель, на которой были получены сигналы рис. 1, изображена на рис. 2 и 3 [2].

Решение обратной задачи сводится к выводу из формулы (1) исходного профиля поверхности z ( x ) :

ln( z _пр( x ))

z ( X ) =      I 0 k ₂ .                   (2)

Г f - f2 Y

I 2 J

ФОРМА ЗОНДА микроскопе или силовое взаимодействие в атомно-силовом микроскопе. С математической точки зрения это означает, что функции, описывающие форму зонда и поверхности, имеют больше одного решения. Начиная с этой точки в случае параболоидальной формы зонда информация о поверхности получается не кончиком зонда, а его гранью. При этом искажения имеют форму функции зонда со знаком минус.

Таким образом, форму зонда можно получить, сканируя эталонную ступенчатую структуру, отфильтровав другие шумы, или получив изображения зонда в электронном микроскопе с заведомо более высокой точностью. Зная функцию или таблицу, задающие форму зонда, можно отфильтровывать искажения, вносимые этим эффектом, находя большие перепады высот, сравнивать профиль грани с формой зонда и вычитать при необходимости.

Данный эффект промоделирован на рис. 5 и 6.

Так как зонд не является идеально тонким стержнем, а имеет форму конуса или параболоида, то форма зонда накладывает погрешность на получаемый профиль поверхности (рис. 4) [1]. Этот эффект возникает из-за взаимодействия между зондом и поверхностью помимо кончика зонда другими его поверхностями. Например, туннелирование электронов в сканирующем туннельном

а

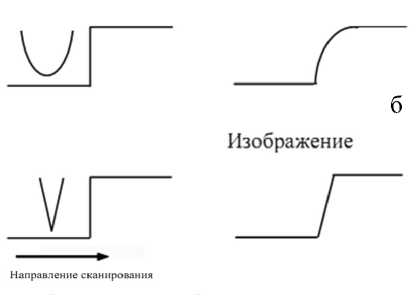
Рис. 4. Типовые искажение, вносимые формой зонда. а — профили зонда и рельефа, б — изображения

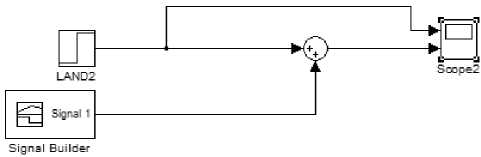
Рис. 5. Модель искажений, вносимых формой зонда

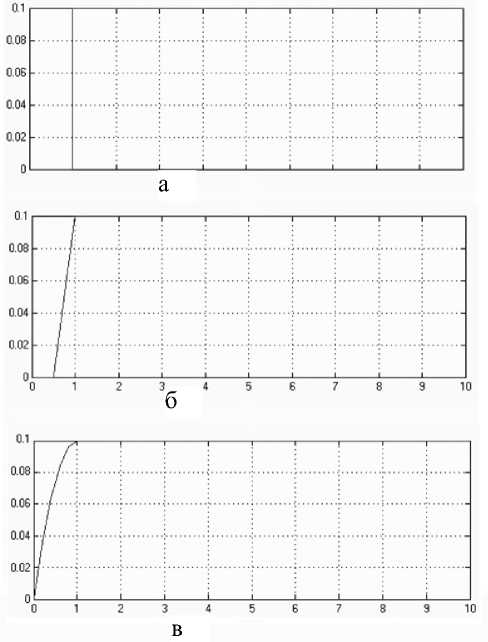
Рис. 6. Искажения, вносимые формой зонда.

а — исходный сигнал; б — искажение зондом треугольной формы; в — искажение зондом параболоидной формы

АППАРАТНАЯ ФУНКЦИЯ СКАНЕРА

Аппаратная функция сканера описывается уравнением mszs = -aszs - ks (zs - YU(t)) ,           (3)

где z s — смещения от положения равновесия сканера с образцом; m s , α s , k s — эффективная масса, коэффициент трения и жесткость колебательной системы сканера с образцом; U ( t ) — управляющее напряжение, приложенное к пьезоэлементу сканера; γ — чувствительность пьезосканера [3].

Зная частоту резонанса сканера (вычисляется из АЧХ сканера) и паспортные данные (масса) можно решить уравнение. Таким образом, решение данного уравнения будет являться решением прямой задачи.

Данный эффект промоделирован (прямая задача) [2] на рис. 7 и 8.

ВОССТАНОВЛЕНИЕ ПРОФИЛЯ

Сигнал реакции сканера можно представить в виде математической свертки импульсной характеристики сканера и входного сигнала — исследуемой поверхности, которая является уравнением Фредгольма 1-го рода:

g ( x ) = h ( x ) • w ( x ),                    (4)

+to

g ( x ) = j h ( x , ю ) w(rn )d ® ,            (5)

-to где w(x) — истинный профиль поверхности; h(x) — ядро уравнения (импульсная характеристика); g(x) — искаженный профиль поверхности.

По теореме Бореля, фурье-образ свертки двух функций равен произведению их фурье-образов. Т. е. если

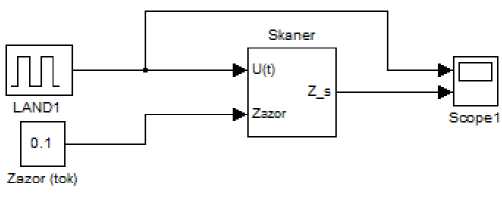
Рис. 7. Модель искажений, вносимых переходной функцией сканера

+to

H(to ) = j h ( x ) e ™ d x             (6)

-to

и

+to

W(ю ) = j w ( x ) e i ^{m x} d x ,               (7)

-to где H(ω) — фурье-образ ядра уравнения (импульсной характеристики), W(ω) — фурье-образ исходного профиля, то

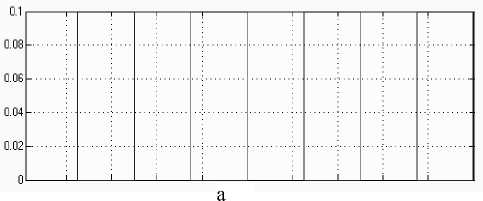
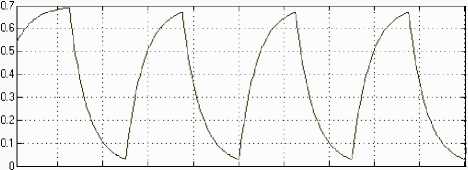
0.2      0.4 O.G 0.8       1        1.2      1.4      1.Б      1.8       2

б

Рис. 8. Искажения, вносимые переходной функцией сканера.

а — исходный профиль поверхности вида , б — искаженный

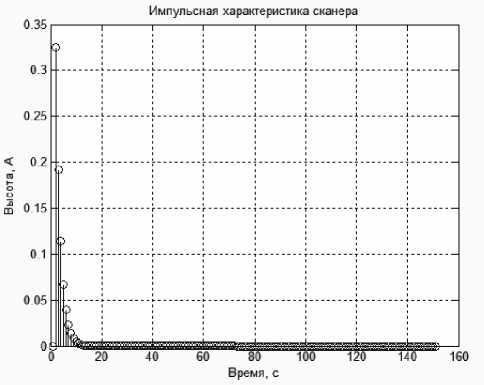
Рис. 9. Импульсная характеристика сканера h ( x )

+to

G " ) = — [ H " )W (" ) e " x d x ,        (8)

2n i сти функции на краях. Уменьшить этот эффект получается при помощи добавления нулевых точек с двух сторон (расширения) [5, с. 252].

где G ( ω ) — фурье-образ искаженного профиля.

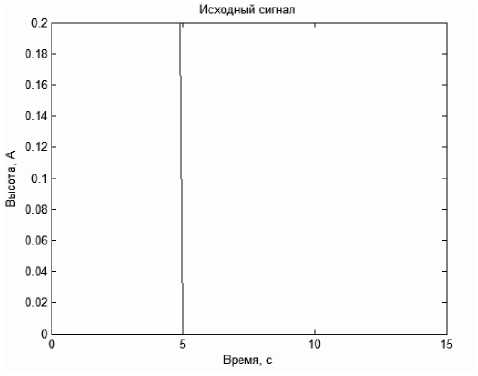
Рис. 10. Исходный профиль поверхности вида

Данное свойство дает возможность косвенного вычисления математической свертки и в дальнейшем решить обратную задачу.

Зная форму переходной характеристики сканера, подбираем подходящий полином z -функции, описывающий известную переходную характеристику. Далее получаем импульсную характеристику сканера (рис. 9) и ее фурье-образ, как в уравнении (6).

Аналогично уравнению (6) запишем фурье-образ искаженного профиля

+to

G" ) = J g ( x ) e i " ^x d x .              (9)

-to

Тогда, решая обратную задачу методом преобразования Фурье (или инверсной фильтрации), искомый профиль поверхности можно записать в виде интегрального уравнения, исходя из уравнений (6)–(9):

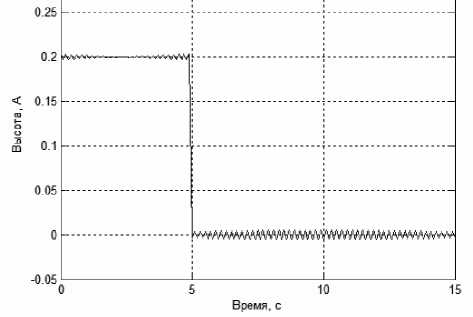
Рис. 11. Восстановленный сигнал профиля ( p = 1, α = 1·E-9, без расширения по краям)

w ( x ) = [ G"e " x d "          (10)

-i h (" )

Рассмотрим поведение спектров. При | ɷ |→0, G ( ɷ ) стремится к некому константному значению "белого шума", а H ( ɷ ) → 0. Это означает, что решение методом преобразования Фурье — неустойчиво и сингулярно. [4, с. 87] При воздействии внешних шумов с некоторой дисперсией на систему неустойчивость решения повышается, т. к. каждому элементу g соответствует не единственный элемент w [5, с. 26] Для устранения неустойчивости можно использовать метод преобразования Фурье с регуляризацией Тихонова. Решение уравнения имеет вид

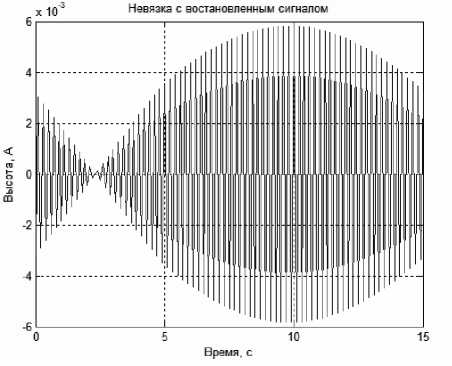
Рис. 12. Невязка исходного сигнала с восстановленным (рис. 11)

w(x) = +[ H(-")G(") e-'"xd", (11) -j\H (" )l2 +a"p , где α > 0 — параметр регуляризации, а p ≥ 0 — порядок регуляризации. При правильном выборе параметров w(x) получается достаточно близким к исходному профилю. [6] На основании вышеизложенных выводов нами было разработано программное обеспечение в среде программирования MatLab. Результаты моделирования представлены на рис. 10–12.

При решении данной задачи мы столкнулись с эффектом Гиббса (рис. 12) — "звоны", или ложные волны. Это связано с разрывом непрерывно-

ВЫВОДЫ

Выявлены параметры математических моделей следующих трех факторов, вносящих искажения в СЗМ-изображения:

• 1)    влияние туннельного эффекта;

• 2)    форма зонда;

• 3)    аппаратная функция системы управления сканером.

Использование этих математических моделей и моделей стандартных воздействий (ступень, треугольник, прямоугольник и т. п.) позволило численно оценить параметры искажений, вносимых рассмотренными факторами, т. е. результаты решений прямых задач. Устранение рассмотренных искажений было выполнено путем решения обратных задач методом Тихонова с различными параметрами регуляризации. Устранение искажения с помощью предложенных алгоритмов предполагается реализовать в программном обеспечении постобработки изображений, полученных методом сканирующей зондовой микроскопии.