Построение АРД-диаграмм для раздельно-совмещенных пьезоэлектрических преобразователей

В области практического применения ультразвуковых методов неразрушающего контроля регламентировано применение диаграмм «амплитуда-расстояние – диаметр» (АРД –диаграммы). Согласно нормативной документации (ГОСТ Р 55725-2013 «Преобразователи ультразвуковые пьезоэлектрические. Общие технические требования») производители пьезоэлектрических преобразователей (ПЭП) обязаны в паспортах на ПЭП предоставлять АРД- диаграмму. В практической диагностике использование данных диаграмм упрощает настройку оборудования, снижает затраты на изготовление настроечных образцов. Данная диаграмма может быть расчетной или полученной экспериментальным путем.

Разработкам АРД-диаграмм посвящены работы российских (Ермолов И.Н., Вопилкин А.Х, Клюев В.В., Алешин Н.П., Данилов В.Н., Воронков В.А.) и иностранных (Крауткремер Й, Крауткре-мер Г.) ученых.

В работах [1 – 8] подробно описаны методики построения АРД- диаграмм для прямых и наклонных совмещенных ПЭП. Для указанных ПЭП авторы подробно исследовали аналитические формулы, позволяющие построить зависимость амплитуды принимаемого сигнала от типов отражателей, расстояний от отражателей до ПЭП. Также в указанных работах представлены обобщенные АРД- диаграммы, при помощи которых возможно построение рабочих диаграмм с учетом геометрических размеров источников ультразвука, диаметров дисковых отражателей и затухания ультразвуковых волн в материале. Остается нерешенным вопрос о построении АРД-диаграмм раздельно-совмещенных ПЭП (РС ПЭП), на которые распространяется требование ГОСТ Р 55725-2013.

Решение указанной проблемы требует описание уравнения акустического тракта РС ПЭП и отражения падающей под углом продольной волны на дисковый отражатель.

В [1 - 8] представлена зависимость амплитуды эхо-сигнала от взаимного расположения плоскости отражателя и источника ультразвука, а также – акустическое поле РС ПЭП, но, используя эти зависимости, авторы не представили уравнение акустического тракта для РС ПЭП.

В [9, 10] решаются вопросы распространения упругих волн в слоистых средах, поэтому решения и научные подходы, представленные в данных работах, могут быть использованы для моделирования распространения и отражения от дискового отражателя продольной волны, что является частью задачи построения АРД – диаграммы РС ПЭП.

В [10] исследовано уравнение акустического тракта дефектоскопа для излучения и приема сигнала при наличии плоской границы, но не рассматривается отражение от дисковых отражателей.

В [11] авторы рассмотрели вопросы, связанные с использованием АРД- диаграмм при эталонировании чувствительности, но не рассмотрели вопросы, связанные с уравнением акустического тракта РС ПЭП.

Исследования, приведенные в работе [13], посвящены рассеиванию волн на неоднородностях, но не рассматриваются вопросы, связанные с уравнением акустического тракта.

В [14] представлен подход к исследованию продольной волны в тонких пластинах с симметричными повреждениями с учетом наклонного падения. В указанной статье представлена модель распространения продольных волн в пластинчатой конструкции, повреждение которой представляет собой симметричное уменьшение толщины. Продольная волна соответствует моде волны Лэмба S0 для низкочастотного диапазона.

В [15] авторы исследуют явления распространения волн в изотропных и анизотропных пластинах, чтобы понять дисперсию направленных волн и подчеркнуть различия, наблюдаемые между структурами.

Результаты работ [14-15] важны для изучения влияния неоднородностей на параметры продольной волны, но для нашей задачи рассмотренные в этих работах подходы не приемлемы, так как в нашем случае продольная волна распространяется полубесконечном теле, а не в ограниченной с двух сторон пластине.

Все выше сказанное указывает на актуальность работ по разработке уравнения акустического тракта РС ПЭП для практических задач неразрушающего ультразвукового контроля.

АКУСТИЧЕСКОЕ ПОЛЕ РАЗДЕЛЬНО-СОВМЕЩЕННОГО ПЬЕЗОЭЛЕКТРИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ

Согласно [2, 3], акустическое поле РС ПЭП рассчитывают, построив мнимые излучатели S\ и ^2 для действительных излучателей s 1и5 9 (расположенных на расстоянии L2 от поверхности объекта контроля и на расстоянии L1 друг от друга) для произвольной точки B (рис.1).

Поле в точке В находят, вычислив расстояния v и r‘’ вдоль лучей c/b и O^B и углы t¹ и&'

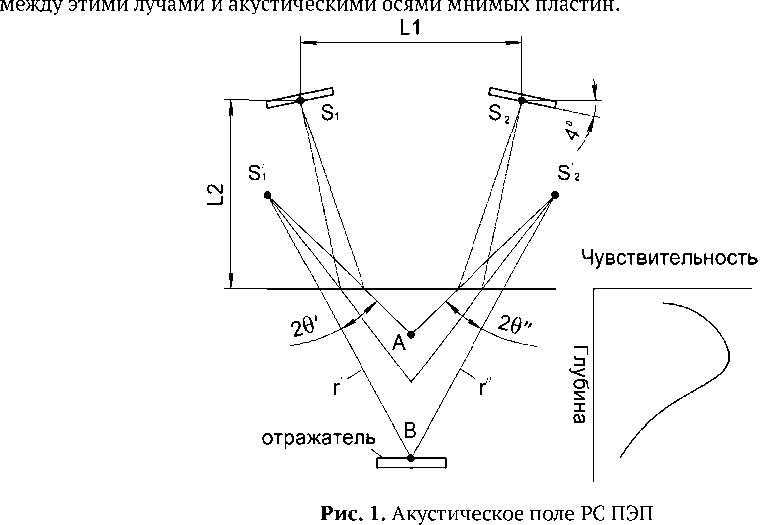
В результате получаем:

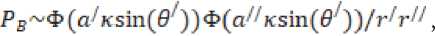
где ли а" - размеры (радиусы) мнимых пьезопластин в основной плоскости (коэффициенты прозрачности не указаны), Φ – функция диаграммы направленности, к = ^ – волновое число, л – длина волны.

Как видно из рис. 1 максимум излучения располагается несколько выше пересечения акустических осей, что объясняется влиянием затухания и расхождения лучей. Еще один важный момент показан на рис.1: отражатель расположен не на оси ПЭП.

Для дальнейших расчетов необходимо рассчитать эхо-сигналы от отражателя, расположенного не на оси преобразователя (наклонных к оси).

ЭХО-СИГНАЛЫ ОТ ОТРАЖАТЕЛЕЙ, РАСПОЛОЖЕННЫХ НЕ НА ОСИ ПРЕОБРАЗОВАТЕЛЯ

Согласно [2,3], общая формула для расчета эхо-сигнала для отражателя в виде диска, расположенного в дальней зоне преобразователя (рис.2) выглядит следующим образом

“ ⁼ jry™^s(P ^— 8) l^(p — 0)|Ф^_(л№т(0))Ф ’ [2&Ksin(p — 9)] ,         (2)

где S _д – площадь источника ультразвука (пьезопластины), S ь – площадь отражателя, R – коэффициент отражения продольной волны, Pq и Р' – амплитуды излученного и принятого сигналов, b – радиус отражателя.

Здесь последний множитель ф ■ определяет диаграмму направленности отражателя, как вторичный излучатель.

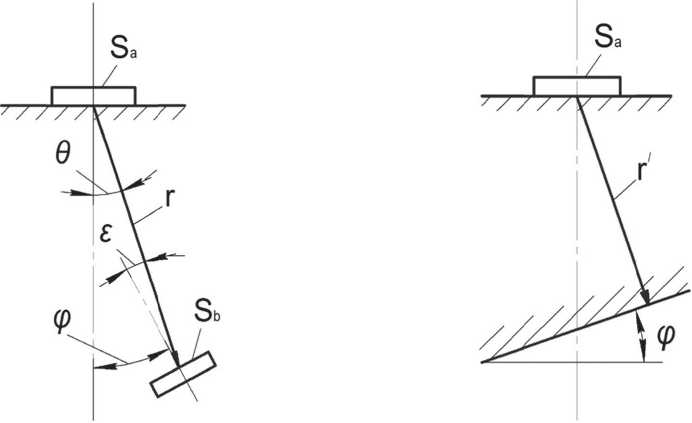
Рис. 2. Схема для расчета эхо-сигнала для наклонного диска

Рис. 3. Схема для расчета эхо-сигнала от наклонной плоскости

Согласно [2], уравнение (2) можно представить в следующим виде:

^ =^СОЗ(Д)сО^)фЧ0)^^^

где £ = <Р — 6 – угол падения на дефект, /1 – функция Бесселя первого порядка.

Так как для расчета АРД – диаграмм необходимо рассчитать величину опорного эхо-сигнала, то для расчета берем отражение от плоскости: как правило за опорный сигнал берется отражение от плоскости меры СО-2, расположенной на глубине 59 мм.

Расчетная схема для опорного сигнала представлена на рис. 3.

Согласно [2], для плоскости, расположенной под углом φ уравнение выглядит следующим образом:

^ =^7СО5(е)ф2^,                      (4)

где Г^ – кратчайшее расстояние от преобразователя до плоскости, S – площадь пьезопластины.

Для дальнейших расчетов необходимо рассчитать коэффициент отражения продольной волны от отражателя.

Согласно [9-10], коэффициент отражения можно рассчитать следующим образом: cosOkj^yi-^Vc ^cos(^

ад=—^-^ , cos(.s)tg^(.2y'H-Lb/(:^ со»(у]

где c^ – скорость продольной волны в металле, Cg – скорость поперечной волны в металле, у = arcsin(—sin(e)) – угол распространения трансформированной поперечной волны.

Для уравнения (1) было отдельно указано, в нем отсутствует коэффициент прозрачности границ для продольной волны. Для точного построения АРД- диаграмм данный коэффициент необходимо учитывать.

Согласно [1], коэффициент прозрачности границ по амплитуде для продольной волны можно рассчитать следующим образом:

^Dii - ;^г2~77 , Д ² ZJ2 CDE(2o_t2)

где A - Z^Zz + Wl+W, , Z_t~ ^Zii cos²{2^ , Z₂ = ——— cos²(2a_tZ) , ^i =-^E^sin²(2fr} , ^{1 z 1}     "       cos^y \ J ‘ cos^) ⁴               cost?) ^{v ;}

w2 =

ли (ли)

sin² ( Zag)^{, z}n — PiQi^{, z}i2 — РдОз^, -tl ^— Pi^il^, -г2 ^— Рз^12, β – угол наклона пье-

зопластины, ^я?2 – угол распространения продольной волны, Cl_t2 – угол распространения поперечной волны, Pl – плотность призмы, fi – плотность металла, Qi – скорость продольной волны в призме, C^ – скорость поперечной волны в призме.

Формулы (1-6) позволяют произвести расчет АРД- диаграмм для заданных РС ПЭП.

РАСЧЕТ АРД-ДИАГРАММ ДЛЯ РС ПЭП

Расчетная схема РС ПЭП представлена на рис. 4.

Используя данные о геометрических характеристиках, акустических и механических свойств серийных РС ПЭП, был произведен расчет для РС ПЭП 112 с частотой 5 МГц, пьезопластиной с диаметром 10 мм, рассеченная на две равные половины. В качестве опорного сигнала был принят эхо-сигнал от плоскости меры СО-2, расположенной на глубине 59 мм.

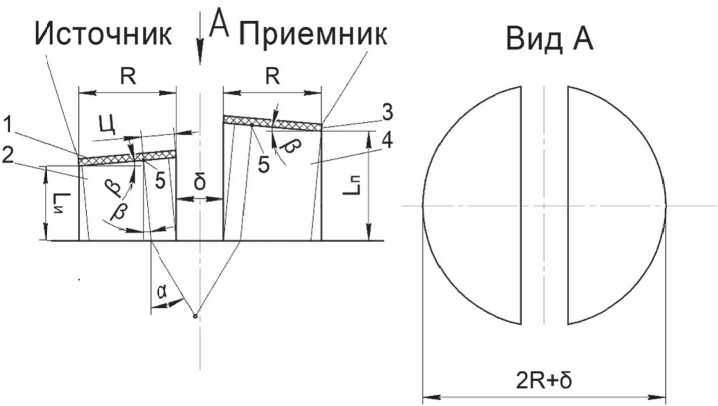
Рис. 4. Расчетная схема РС ПЭП:

1– пьезопластина источника, 2 – призма источника, 3 – пьезопластина приемника, 4 – призма приемника, 5 – точка центра масс источника, δ – зазор между призмами (необходим для размещения акустического изолятора и электромагнитного экрана), Ц – центр масс, ^ и – высота источника, ^n – высота приемника

Разница амплитуд A между эхо-сигналами от дискового отражателя A и плоскости меры СО-2 (опорного) ■Ann рассчитывалась по формуле: А Ад ADn, используя формулы (1-6).

Результаты расчета представлены на рис. 5.

Для проверки результатов расчетов была проведена экспериментальная проверка.

ЭКСПЕРИМЕТАЛЬНАЯ ПРОВЕРКА РЕЗУЛЬТАТОВ РАСЧЕТОВ

Целью проведения эксперимента являлась проверка правильности расчета АРД-диаграммы.

Задачей эксперимента являлась: измерение разницы амплитуды сигнала от дискового отражателя и опорного эхо-сигнала от плоскости меры СО-2, расположенной на глубине 59 мм.

Для измерения амплитуды эхо-сигналов был изготовлен образец (рис. 6) из Ст-3.

Схема эксперимента представлена на рис 7.

В качестве оборудования применялся дефектоскоп UCD -50, мера СО-2 и ПЭП-112-5-10/2.

Исследования проводились на частоте 5 МГц.

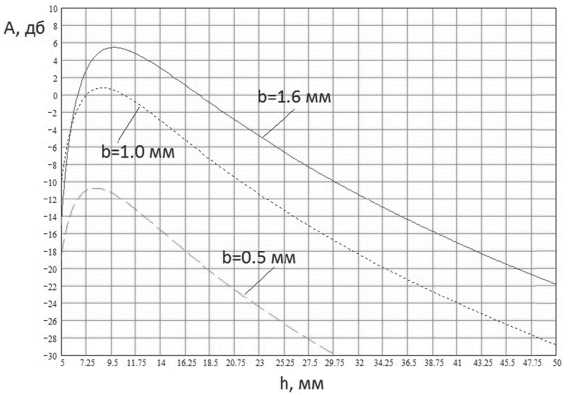
Рис. 5. АРД – диаграмма для РС ПЭП 112-5-10/2, где h – глубина нахождения дискового отражателя диаметром b

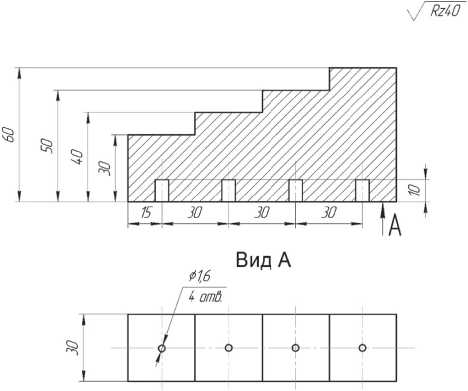
Рис. 6. Ступенчатый образец с дисковыми отражателями

Измерения проводились для дискового отражателя d=1.6 мм в четырех позициях, согласно рис. 7. Позиция 1- глубина залегания отражателя 20 мм, позиция 2- 30 мм, позиция 3- 40 мм, позиция 4 – 50 мм.

Измерение опорного сигнала проводилась при помощи меры СО-2 согласно рис. 8.

В таблице 1 представлены результаты измерения изменения разницы амплитуд между эхо-сигналом дискового отражателя b=1.6 мм и опорным сигналом.

ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

В результате проведения экспериментов выяснилось, что максимальная относительная погрешность составила не более 8 %, что подтверждает правильность составленной расчетной модели расчета эхо-сигналов от от- ражателей в виде диска и плоскости для РС ПЭП. Однако данная модель не учитывает разницу затухания продольных волн между контрольным образцом с дисковыми отражателями и мерой СО-2. В нашем случае затухание в образце с отражателями и СО-2 было одинаковым. В случае, если материал изготовления объекта контроля и меры СО-2 имеют различия, то необходим пересчет значений АРД- диаграммы. Методика пересчета подробно представлена в работах [1-5] и рекомендуется для применения. Другим подходом, позволяющим исключить влияние разницы затухания между объектом контроля и СО-2, является изготовление СО-2 или специального плоскостного отражателя эхо-сигналов (для получения опорного сигнала) из материала изготовления объекта контроля

ВЫВОДЫ

• 1.    В результате проведенного моделирования процесса распространения продольной волны и ее отражения от дискового и плоскостного отражателей получены формулы для расчета эхо-сигналов от указанных отражателей для РС ПЭП.

• 2.    Теоретически рассчитана АРД – диаграмма для РС ПЭП 112-5-10/5 для материала объекта контроля Ст 20. Экспериментальная проверка для данного типа ПЭП показала, что максимальная погрешность измерения разницы эхо-сигнала от отражателя диаметром 1.6 мм, расположенного на глубинах 20, 30, 40 и 50 мм, и опорным сигналом от плоскости, расположенной на глубине 59 мм, составила не более 8 %. Таким образом, предлагаемый подход к построению АРД- диаграмм для РС ПЭП показал свою актуальность и применимость в практической диагностике.

Таблица 1. Расчетные и экспериментальные значения разницы амплитуд эхо-сигналов между дисковым отражателем и опорным сигналом

Диаметр отражателя, мм	Глубина залегания отражателя, мм	Разница амплитуд A расчетная, дб	Разница амплитуд A экспериментальная, дб	Относительная погрешность, %
1.6	20	-2.3	-2.5	8
1.6	30	-10.1	9.5	6
1.6	40	-16.5	17	3
1.6	50	21.8	20.5	6