Построение диаграммы предельных деформаций формоизменения листовых заготовок из авиационных алюминиевых сплавов

проекту СП-2200.2022.5 «Разработка моделей и алгоритмов расчёта пластического формообразования заготовок штамповочного производства».

Original article

Construction of Forming Limit Diagram for Sheet Blanks from Aviation Aluminum Alloys

Sergey I Feoktistov , Ivan K Andrianov M

Introduction . The modern development of stamping aircraft manufacturing is inextricably linked with the assessment of the limiting capabilities of sheet blanks. However, the issue of defect-free forming of blanks made of aviation aluminum alloys is understudied. The importance of this issue is due to the fact that aluminum alloys are often used in the manufacture of thin-walled products for aviation purposes. During the implementation of shaping processes, various defects may appear, specifically, corrugation or unacceptable thinning. In this regard, the objective of the work was to construct a diagram of the limit deformations of the base aviation alloys and to conduct a comparative analysis of the limit deformation curves for these materials.

Materials and Methods. Logarithmic deformations with the property of additivity were used to account for large deformations. The construction of the diagram of the limit deformations was carried out in the formulation of the deformation theory of plasticity. The issue of constructing a diagram of limit deformations was considered on the basis of the positivity criterion of the loading force derivative. In the area of negative values of the smallest major deformations, the Hill criterion was used to construct the limit deformation curve, and in the area of positive values of the smallest major logarithmic deformations, the Swift criterion was used. When constructing the limit deformation diagram, a power approximation of the hardening rule was used.

Results . The curves of limiting deformations for the following aviation alloys were obtained: AMg6, D16AT, AMg2M, 1201-T, AMcM. According to the comparative analysis of the areas of safe forming, the values of deformations of the beginning of necking and their influence on the change in the position of the curve of the limiting deformation of blanks were compared: the greater the deformation of the neck formation, the higher the position of the curve of the limiting deformations. The concept of the Keeler's limit deformation diagram was described. Approaches to the construction of the Hill-Swift criteria used on the basis of the results of tensile testing of sheet specimens were presented.

Discussion and Conclusions. Based on the constructed curves of limiting deformations for aviation alloys, AMg-6, D16AT, AMg2M, 1201-T, AMcM, the following has been found. AMg2M alloy has the largest area of safe forming, 1201-T alloy has the smallest one. That is explained by the difference in relative deformations of the beginning of neck formation. The conducted research made it possible to evaluate the possibilities of defect-free forming of thin-walled blanks made of basic aviation aluminum alloys. The use of the constructed diagrams of limiting deformation will provide predicting the appearance of breaks in the process of forming sheet blanks.

Acknowledgements . Appreciation is expressed to the “Council for grants of the President of the Russian Federation for state support of young Russian scientists and for state support of leading scientific schools of the Russian Federation” for financial support of the research under scholarship project SP-2200.2022.5 “Development of models and algorithms for calculating the plastic shaping of blanks for stamping production”.

Введение. Современное развитие авиационного производства неразрывно связано с исследованием процессов листовой штамповки. Одной из основных проблем в задаче формообразования является прогнозирование дефектов, в частности, утонений, разрывов, гофрообразования. Данные вопросы связаны с оценкой предельных возможностей заготовки. Под предельным формообразованием листовой заготовки будем понимать способность материала деформироваться до требуемой геометрии без шейкообразования или разрушения.

На сегодняшний день проблема прогнозирования дефектов листовых заготовок в процессе штамповки решается с помощью следующих методов:

• -    эмпирических, основанных на механических испытаниях на простое растяжение металлических образцов, тонких листов и лент, испытаний на изгиб, а также методов испытаний труб на раздачу и протяжку;

• -    теоретико-эмпирических, которые основаны на использовании и распространении результатов испытаний образцов на одноосное растяжение на другие схемы деформирования заготовок;

• -    теоретических, в основе которых лежит использование критериев предельного деформирования, в частности, при изготовлении тонкостенных изделий. Основоположниками этих методов были Дж. Закс, Р. Хилл, А. Д. Томленов, В. Д. Головлев, Г. Д. Дель, З. Марчиняк, А. Д. Матвеев, Дж. Д. Любан [1–20].

Следует отметить, что недостатком эмпирических и теоретико-эмпирических методов является ограниченный круг использования результатов.

Наиболее важным шагом в решении вопроса прогнозирования дефектов тонкостенных изделий стала разработка концепции диаграммы предельных деформаций (FLD), предложенная Килером [16–20], которая на сегодняшний день является общепринятой в решении задач листовой штамповки. FLD-диаграммы широко используются в CAE-программных системах AUTOFORM и PAM-STAMP 2G.

Экспериментальные методы построения диаграмм деформирования основываются на методике испытаний, представленных в трудах Марчиняка и Наказимы. Следует также отметить, что вопросы пластического разрушения листовых заготовок рассматривались в [17–19]. В последнее десятилетие интерес к построению FLD-диаграмм существенно вырос, большинство зарубежных исследований направлено на экспериментальное построение диаграмм для конкретных материалов, а также численное моделирование процессов формоизменения с помощью конечно-элементных методов, что отражено в трудах [20–30]. Теоретические аспекты построения FLD-диаграмм и диаграмм деформирования III рода представлены в работах [31, 32].

Важно отметить, что диаграмма предельных деформаций позволяет оценить начало шейкообразования, которое в процессе деформирования заканчивается разрушением образца. FLD-диаграмма связывает значения главных логарифмических деформаций, действующих в плоскости листа. Диаграммы предельных деформаций позволяют не только прогнозировать разрушение заготовки, но и оценивать наличие других дефектов, в частности, складкообразование, утонения, которые, в свою очередь, понижают качество штампуемой детали. Основными зонами FLD-диаграммы являются зоны разрушений, возможных разрывов, безопасного формоизменения, вероятного образования складок и складкообразования (рис. 1) [31].

е 1

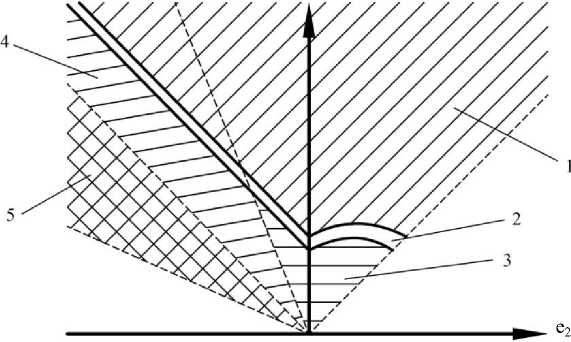
Рис. 1. Диаграмма предельных деформаций: 1 — зона разрушений; 2 — зона возможных разрывов;

3 — зона безопасного формообразования; 4 — зона вероятного образования складок; 5 — зона складкообразования [31]

Механика

Материалы и методы. При описании процессов формообразования тонкостенных заготовок момент перехода в стадию пластичности определяется в соответствии с критерием Губера-фон Мизеса [33]:

at = Т'^Г+^Т-^^ = О"Т , где а1, a2 — главные истинные напряжения, при а3 = 0 ввиду малой толщин заготовки; ai — интенсивность истинных напряжений; аТ — предел текучести.

В соответствии с деформационной теорией пластичности зависимость между интенсивностью напряжений и интенсивностью логарифмических деформаций определяется как:

^^i-^)'

^F^-?1)'

I'

где е1, е2, — главные деформации.

Поскольку в задачах листовой штамповки процессы формоизменения могут происходить в несколько переходов, поэтому рассматриваются большие деформации. Применение относительных деформаций недопустимо. В связи с этим деформированное состояние в (1) представлено в истинных логарифмических деформациях.

Интенсивность главных деформаций:

6i = -=/62 + е2 +6162.

Отношение главных деформаций и главных истинных напряжений:

а = |,0 = ^.

На основании соотношения (1) и (2), связь между а и /? определяется:

2а+1

^в     2+а .

Согласно выражению (2), критерий Губера-Мизеса имеет вид:

O = 01^1 - в + в2 = От ,

а интенсивность деформаций:

-7=6^1 + а + а2.

Для оценки начала шейкообразования на сегодняшний день используется критерий положительности производной силы нагружения, основоположниками которого являются Дж. Закс и Дж. Д. Любан [17]. Cогласно описанному критерию, деформирование образца является устойчивым при положительном приращении растягивающего усилия. Момент неустойчивого деформирования с последующим растяжением начинается при ДР = 0 и продолжается при ДР < 0 (рис. 2).

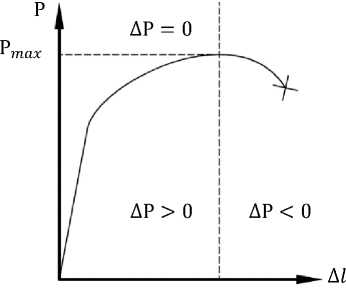
Рис. 2. Индикаторная диаграмма одноосного растяжения образца [33]

Диаграмму деформирования алюминиевых сплавов, получаемую по результатам испытания на одноосное растяжение, при теоретическом анализе диаграмм предельных деформаций формоизменения аппроксимируют степенной функцией [18, 19, 31, 32]:

as = Ае” или ai = Ае”,

где a_s = P/F — истинное напряжение; Р — растягивающее усилие; F — текущая площадь сечения образца; е = ln(1 + Д1/1 0 ) , а А и п — коэффициенты степенной аппроксимации.

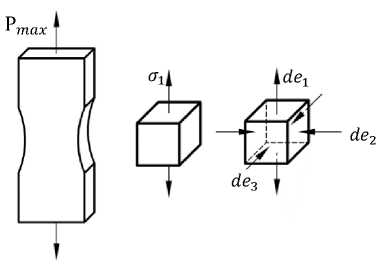
Используя критерий положительности производной силы нагружения и степенную аппроксимацию диаграммы деформирования III рода, можно получить связь между предельной деформацией образца в момент возникновения рассеянной шейки и коэффициентом степенной аппроксимации n при условии ДР = 0 (рис. 3) [32]:

^е ш ^e im ^- ⁽⁵⁾

Важно отметить, что соотношение (1) выполняется при использовании логарифмических деформаций. В случае использования относительных деформаций возможно только приближенное равенство.

а)

б)

в)

Рис. 3. Возникновение рассеянной шейки при одноосном растяжении плоского образца: а — образец; б — напряженное состояние; в — деформированное состояние [33]

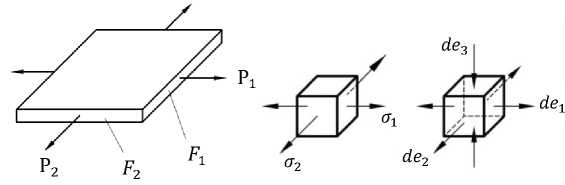
Рассмотрим напряженное состояние пластины, к которой по краям приложены два растягивающих усилия, т.е. заготовка испытывает двухосное растяжение (рис. 4).

а)                             б)                      в)

Рис. 4. Напряженно-деформированное состояние пластины при двухосном растяжении: а — пластина; б — напряженное состояние; в — деформированное состояние [33 ]

Используя критерий положительности производной силы нагружения, определим величину предельной деформации е ^ш в момент, когда силы Р₁ или Р₂ максимальны. Для случая, когда Р 2 /Р 1 = const, Р₂/Р₁ = const, в момент максимума растягивающих усилий dP₁ = dP₂ = 0. Г. В. Свифтом [19] предложено соотношение для предельной деформации:

(1-Р+Р²)^{3/2 е} ш = 4^4 - 3р - 3р² + 4p^3.

Согласно выражениям (2)–(4), соотношение для описания кривой предельных деформаций при различных показателях степенной аппроксимации в зоне упрочнения имеет вид:

4⁽e i - п⁾⁽е 2 + 2еО³ - 3⁽e i - 2n⁾⁽e i + 2е 2 ⁾⁽е 2 + 2e i )² -

-3(е₁ + 2п)(е 2 + 2е₁)(е₁ + 2е₂)² + 2(2е₁ + п)(е 1 + 2е₂)³ = 0.                     (6)

Из экспериментальных и теоретических работ известно, что после возникновения рассеянной шейки пластическая деформация образца продолжается. В дальнейшем может возникнуть локализованная шейка, которая отличается от рассеянной не только размерами, но и тем, что её возникновение и развитие осуществляются в условиях плоской деформации при интенсивном утонении образца по толщине.

Механика

Согласно исследованиям Р. Хилла [20], критерий предельного деформирования определяется моментом образования локальной шейки, при котором приращение суммарного усилия равно нулю. В этом случае соотношение для предельной деформации определяется выражением:

е„=2^^:- ;7''' ' ’.                                                        (7)

С учетом выражений (2), (4), выражение (7) для построения диаграммы предельных деформации по критерию Хилла имеет вид:

C 1 + C 2 — и = 0.                                               (8)

Следует также отметить, что описанный подход согласуется с методом конечных элементов, который широко применяется для построения FLD-диаграмм различных материалов в последние годы [21–29].

Результаты исследования. На практике построение FLD-диаграммы будем осуществлять с использованием двух критериев [31], а именно: критерия Хилла, который используется при е₂< 0 согласно (8); критерия Свифта, который используется при е₂ > 0 согласно (6) . Рассмотрим применение данных соотношений для построения кривой предельных деформаций широко используемых в авиационной промышленности алюминиевых сплавов при известных значениях деформации шейкообразования: Е ш = 0,18 (АМг-6), Е ш = 0,16 (Д16АТ), Е ш = 0,2 (АМг2М), Е ш = 0,06 (1201-Т), Е ш = 0,1 (АМцМ) [34].

Определяя е ш по формуле е ш = ln(1 + Е ш ) и используя выражение (5), получим значение показателей деформационного упрочнения: и = 0,17 (АМг-6), и = 0,15 (Д16АТ), и = 0,18 (АМг2М), и = 0,06 (1201-Т), и = 0,09 (АМцМ). Тогда диаграмма Хилла-Свифта, согласно (6), (8), примет вид, изображенный на рис. 5.

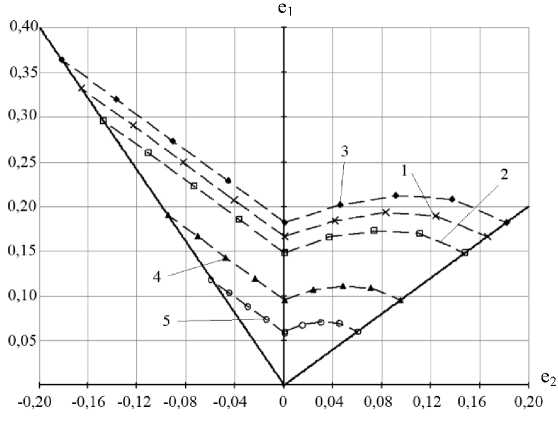
Рис. 5. FLD-диаграммы Хилла-Свифта для различных авиационных сплавов:

1 — АМг-6; 2 — Д16АТ; 3 — АМг2М; 4 — 1201-Т; 5 — АМцМ

Обсуждение и заключения. Согласно построенным кривым предельных деформаций наибольшая область безопасного формоизменения из пяти исследуемых сплавов у сплава АМг2М, наименьшая — у сплава 1201-Т, что обусловлено различиями в деформационных свойствах материалов, в частности, отличием деформаций начала шейкообразования. У сплава АМг2М относительная деформация начала шейкообразования составляет 20 %, а у сплава 1201-Т — 6 %.

Таким образом, на основании данных о кривых упрочнения, степенной аппроксимации и деформации шейкообразования для авиационных алюминиевых сплавов АМг-6, Д16АТ, АМг2М, 1201-Т, АМцМ построены кривые предельных деформаций формоизменения, позволяющие определить зону безопасного деформирования листовых заготовок. Результаты исследования имеют практическую значимость при решении задач листовой штамповки для данных материалов с целью прогнозирования недопустимых утонений, разрывов и складкообразований тонкостенных заготовок.