Построение геоинформационной математической модели транспортной инфраструктуры

Известны различные типы математических моделей сложных систем, конкретный вид которых обусловлен областью их приложения, степенью охвата факторов, подробностью отображений физических явлений и целями исследования. Выделим базовые общесистемные принципы построения подобных моделей:

. разделение системы на функциональные объекты и связи;

. декомпозиция сложных систем;

. стратификация модели по уровням пред ставлений;

. формирование стратифицированных про странств состояний.

Решение задачи модификации улично-дорож

-

-

ной сети требует представления исследуемой предметной области в виде структурированной цифровой модели. Математическая модель транспортной инфраструктуры представляется совокупностью трех составляющих { © , 5 , O } : 0 - улично-дорожная сеть; 5 - макромодель транспортного потока; O - дорожные объекты.

Улично-дорожная сеть 0 - это совокупность 3-х множеств | © X , V , e } : участков дороги, узлов и дуг, соответственно. Элементы каждого множества имеют определенный набор параметров. Причем 0 i может представлять как всю улично-дорожную сеть города, так и отдельные его части вплоть до границ одного участка 0^ . Разделение участка на более мелкие участки проводится по параметрам других составляющих модели и обусловлено условием решаемой задачи. Вид перекрестка обусловлен только его кон-

фигурацией: количеством дуг и узлов, количеством примыкающих участков, при этом концептуальная модель улично-дорожной сети остается неизменной.

Триада | © X , V, E } является базисом математической модели транспортной инфраструктуры, все остальные объекты так или иначе привязаны к этому базису (рис. 1).

Участок 0 .X Е 0 X - полигональный участок улично-дорожной сети, представленный набором координатных пар, описываемый единым набором физических параметров. Для автомобильных транспортных задач достаточно рассмотрения участков в двумерном евклидовом пространстве.

Таким образом, геометрическая составляющая математической модели участка:

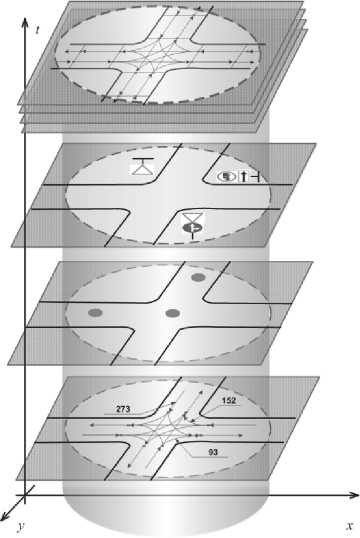
Рис. 1. Разнотипные объекты транспортной инфраструктуры в базисе улично-дорожной сети

G^e‘ (ё^Г^., ё )■ (1) где Г ( XL X ’ Y ^j ) ’ * = 1, M ⁶ ’ j = 1 № вершины полигона;

( X tj , Y t ) - координаты вершин полигона; M ⁶ число участков улично-дорожной сети, Nf число вершин полигона * -го участка.

В дополнении к геометрическим параметрам участок t X обладает следующим набором имманентных свойств:

. тип T i е {1, 2,3,4} , где 1 — перегон, 2 - перекресток, 3 – пешеходный переход, 4 – железнодорожный переезд;

. уровень L ⁶ * е { — 1, 0,1, 2,..., l } ;

. величина угла уклона а^е‘ е [0, j] ;

X

. величина угла подъема ^ ■ е [0, j] ;

X

. коэффициент безопасности K е [0, 1] ;

. список соседних участков, непосредственно граничащих с ним, с⁶ * е S^{lx r} , где S^lxr множество векторов размера r .

Исходя из этого, математическая модель полигонального участка t выглядит следующим образом:

X XX   X   X   X   X tX(Gt ,Tt ,L ,^‘ ,^‘ ,Ke; ,C6i ). (2)

Узел vk е V является вершиной ориентированного графа, канализирующего транспортные потоки. Для УДС узел – место разделения потоков транспортных средств, всегда (кроме крайних случаев – тупиков УДС) лежит на стыке двух участков и показывает возможность движения с одного участка на другой в направлении, определяемом соответствующей дугой.

Двум соседним участкам поставлены в соответствие один или два узла. Более того, узел име- ет характеристику, показывающую взаимное расположение участков. Исходя из этого, узел обладает следующими имманентными свойствами:

. принадлежность к участкам, между кото- рыми расположен узел

{ 6 ^X , 6 ^Х } , где 6 X , 6 Х е 6 ^X ,

0 ^х .. , © X *6 , г , j = 1, M ⁶ ;         „

. величина угла между участками y v е [0, ^ ") .

Таким образом, математическая модель узла имеет вид:

v _k ( 6 X , 6 X , fv ) ,             (3)

где к = 1 N V , N V число узлов улично-дорожной сети.

Дуга el е E это элемент ориентированного графа, задающий направление движения транспортного потока на участке и содержащий соответствующие характеристики. Двум узлам поставлена в соответствие одна дуга, определяющая направление движения транспортного средства, либо две дуги, определяющие место разворота (смены направления движения). По одному участку может проходить несколько дуг (потоков), но дуга может находиться только внутри единственного участка. Далее перечислены имманентные свойства дуги:

. начальный и коне чный узлы дуги { V * , V j } , где v,, у ^е V , i , j = 1, n^v ;

. радиус кр ивиз ны _R ^e l (если дуга прямая, то R e =0), где l = 1 N E , N E число дуг улично-дорожной сети;

. количество полос движения N _r ^{e l} ;

. расстояние видимости L ^e _v ^l ;

. признак наличия велосипедной дорожки F b^l е {0,1} ;

. признак наличия пешеходной дорожки F pe е {0,1} ;

. признак наличия полосы для транспортных средств общего пользования F l е {0,1} ;

. признак наличия реверсивной полосы F е {0,1} ;

. признак запрета движения транспорта Ff е {0,1} .

Математическая модель дуги:

el       el el el el el el el el (v, Vj , R , Nr , Lv , Fb , Fp , Fc , Fr , Fu ) . (4)

В рамках макроскопического подхода транспортный поток S = { ~ * .}, i = 1,2,..., n , движущийся по улично-дорожной сети дугам e ~ _i е E , характеризуется общей средней скоростью v , плотностью потока k и интенсивностью движения I в определенный момент времени в определенном месте улично-дорожной сети. Пусть О = { o *^X } , ( O ~ ^ 0 ) - множество дорожных объектов, оказывающих прямое или опосредованное влияние (управление) на транспортный поток S ~ . Дорожные объекты дислоцированы на улично-дорожной сети – на дугах ~ . е E орграфа G , содержащее в себе следующие подмножества:

Q¹ q О) - множество дорожных объектов -инциденты;

O S q О) - множество дорожных объектов -предприятия автотранспортного сервиса;

O T С О) - множество дорожных объектов -технические средства организации дорожного движения.

Влияние может быть разной природы: управляющим, вносящим помехи или способствующим беспрепятственному проезду. Влияние может оказывать как положительное, так и отрицательное воздействие на транспортный поток.

В общем случае дорожный объект описывается своим местоположением в базисе

I © X , V , E j и рядом атрибутов, специфичных для конкретного типа дорожного объекта. Существует единственная дуга ~ E E орграфа G , на которой расположен дорожный объект.

Рассмотрим построение математической моделей для задачи пространственного анализа интенсивности движения транспортных потоков. Задача состоит в построении прогнозирующей модели нахождения интенсивности движения I по параметрам объектов, составляющих уличнодорожную сеть © , и по дислокации дорожных объектов O . При построении модели рассматривается участок ('’ типа перекресток ( т( _ 2) и ближайшие соседние к нему участки. Модель строится с учетом инвариантности к номеру участка i , чтобы была возможность применения модели для любого типа перекрестка улично-дорожной сети. Для удовлетворения этого требования необходимо обобщить параметры объектов, взаимное расположение которых изменяется в зависимости от номера рассматриваемого участка. Это требует вычисления определенной функции от параметров, которая может варьироваться в зависимости от типа параметров, объекта которому они принадлежат и расположении объекта в рассматриваемой модели.

В модель входят без изменений величина угла X^X уклона а ■ , величина угла подъема К⁸ и коэффициент безопасности K ( рассматриваемого участка 8 X •

Параметры соседних участков необходимо обобщить. Ощутимый вклад в модель вносят углы уклона и подъема максимальной величины, поэтому их обобщенное значение вычисляются следующим образом:

^             / p^ \ zi С              / А X х а. _ max(a m), р. _ max (р m ), (5) mEMC                 mЕ M C где MC E {m1, m 2,..., mr} индексы соседних к 8X участков.

Обобщенный коэффициент безопасности вычисляется как среднее значение коэффициентов соседних участков:

К = 1 V к' s,                            s , ri mЕMC

X где r размер вектора соседних к участку 8 участков.

В модель необходимо ввести параметры узлов. В рамках математической модели простран- ственного анализа интенсивности интересны обобщенное значение угла между участком Ар и соседними участками и обобщенное значение угла между соседними участками и следующими за ними участками.

Обобщенное значение углов вычисляется как максимум из всех углов, участвующих в отборе:

Y.FC _ max (Yv ) , rSC _ max (Г), (7) lE LF          ’             lE LSC          ,    \ / где ^CE {l1,Z2,.../2r}- индексы узлов, лежащих на границе участка Ар с соседними участками;

L SC Е { 1 1 , l ₂,..., l ₂ r } — индексы узлов, лежащих на границе соседних участков со следующими за ними участками.

Математическая модель содержит параметры дуг рассматриваемого участка улично-дорожной сети, при этом дуги делятся на три категории:

• -    дуги участка Ар ;

• -    дуги соседних участков, входящие в участок ( p

• - дуги соседних участков, исходящие из участка Ар .

Обобщение параметров проходит в пределах каждой категории. Чем меньше радиус кривизны, тем критичнее вклад параметра в результат, поэтому обобщенное значение вычисляется следующим образом:

R C _ min( R e n ) Rp _ min( R e n )

nE N C         ,            nE N*C          '

R OC ^_ mi ⁿ⁽ R e n ) , при R e n _# 0 ,        (8)

nE NOC где RiC , RiIC , RiOC обобщенные радиусы кривиз-XX ны дуг участка Ц , дуг входящих в участок ui и дуг, выходящих из участка Ар, соответственно;

N C , N IC , N OC индексы дуг участка (Xp , входящих и выходящих дуг, соответственно.

Количество полос движения усредняется и вычисляется по формулам

N C

_L ^ n:v NrC_ 1 ^ N p nE NC en r,

p

n E N ^IC

N^OC =--- У N

' r, i     -OC ^ly‘ p   nEN OC где NrCi , NrICi , NrOiC среднее количество полос на

, px ,      , участке и , дуг входящих в участок и и дуг вы-iXi ходящих из участка и , соответственно;

C IC OC iX p , p , p число дуг на участке ( , входя- щих и выходящих дуг, соответственно.

Чем меньше расстояние видимости, тем кри- тичнее вклад данного параметра в результат, поэтому при вычислении обобщенного значения выбирается минимальное значение из возможных:

LC _ min(Le; ) LC _ min(Len ) vis, i                    vis , vis, ivis nE NC             v s,     nE NIC v s

LOCC,i_ minc(LViS),(10)

,       nE NO

Для ввода в математическую модель признаков наличия велосипедной дорожки, пешеходной дорожки, полосы для транспортных средств общего пользования, реверсивной полосы или запрета движения грузового транспорта для каждого типа признака в каждой группе дуг используется кумулятивная характеристика p s,C

¹ k, i

U Fe n e Ns, C

где s указывает группу дуг, k e {bic, ped, bus, rev, crg} указывает на соответствующий тип признака. Другими словами, параметр равен единице, если хотя бы один параметр соответствующего типа в группе равен единице.

При разработке математической модели пространственного анализа интенсивности рассматриваются только статичные во времени дорожные объекты O , поэтому инциденты исключены из модели. Каждый дорожный объект oi имеют ссылку на дугу el , рядом с которой он находится (к которой привязан). Используя эту связь можно получить дорожные объекты, рас-X положенные на исследуемом участке Ui и на соседних к нему участках. Присутствие того или иного объекта oi на дуге el можно представить в виде бинарной переменной. Обобщение параметров внутри групп дуг производится аналогично признакам дуг. Предприятия автотранспортного сервиса не могут находиться непосредственно на перекрестке, поэтому объекты множества OS учитываются только на соседних участках.

Отдельного рассмотрения требуют дорожные знаки. Каждый тип дорожного знака имеет определенную степень влияния на транспортный поток s . Для поиска коэффициентов, определяющих степень влияния дорожного знака, использован метод экспертных оценок [4]. Для каждой дуги рассчитывается усредненный параметр, исходя из дислоцированных на нем дорожных знаков:

F:- = vr 2 Fsenki,       (12)

N    ie Is где Fei e {0,1} - булевская переменная, показывающая наличие ( Fs"i = 1) или отсутствие

( F_sn = 0 ) i-го типа знака на дуге e_n;

ke[0,1] – коэффициент, показывающий степень влияния i-го типа дорожного знака на транспортный поток S;

_I^S – множество всех типов знаков;

N ^S – количество дорожных знаков, ссылающихся на дугу e_n .

С использованием разработанной модели, решается задача модификации улично-дорожной сети города. На основе существующей улично-дорожной сети и с учетом параметров транспортного потока, рассчитываются акупунктурные точки города (точки притяжения транспортных потоков). Совокупность разнотипных объектов транспортной инфраструктуры и полученные акупунктурные точки служат входными параметрами задачи локализации дорог транспортной сети.