Построение и анализ некоторых точных аналитических решений двумерных упругих задач в рамках континуума Коссера

In this paper a new method is proposed to develop exact analytical solutions to two-dimensional elastic problems in the context of nonsymmctrical elastic theory. The solutions under study are represented as truncated Fourier series in terms of angular coordinates. A system of differential equations has been constructed to define the coefficients of Fourier series. It has been shown that this system can be solved in terms of Bessel functions. Some example problems have been solved to show the potential of the method proposed.

Задачи о деформировании материала, при котором играют значительную тюль векторы перемещения и вращения частиц среды, а тензоры деформаций и напряжений являются несимметричными, давно привлекают внимание исследователей. Деформация такой среды, впервые введенной братьями Коссера в 1910 г., описывается не только вектором перемещения и,но также вектором поворота й). Среду, моделируемую таким образом, сегодня часто называют средой Коссера, а за теорией в русскоязычной литературе закрепились названия моментной, или несимметричной теории упругости.

В 60-70-х гг. эта теория была развита независимо несколькими исследователями: W. Nowacki [8] и рядом его учеников, Е.В. Кувшинским и Э.Л. Аэро [2]. В..А. Пальмовым [9], [10], Н.Ф. Морозовым [6] и др. В это же время появились первые аналитические решения плоских задач в рамках данной теории. Однако большинство точных решений, известных на сегодня, получены с использованием упрощения, часто называемого "стесненным вращением" или средой псевдокоссера. при котором постулируется зависимость вектора вращения от вектора перемещения:

C0= — rot и. (I) 2

Этот вариант моментной теории упругости понижает се полноту, гак как [! ij число физических констант для изотропного упругого тела сокращается с шести до четырех. Кроме этого, получаемая структура уравнений такова [8], что если, в частности, на поверхности упругого тела заданы перемещения, то нс удастся независимо выразить нормальную составляющую вектора поворота.

Данная работа посвящена отысканию точных аналитических решений для тел вращения в полной моментной постановке. Предполагается, что напряженно-деформированное состояние э тих тел в цилиндрической системе координат ур,о, л)

зависит только от координат риф. Данный класс задач характеризуется тем. что решение для него можно представить в виде отрезка ряда Фурье:

и(р, ф) = {ир (р, ф), и^ (р, ф), 0], и, (р, Ф) = (7(0)(р) + и{" (р) соз(ф) + ^    (р) сов(нф), н=2

< и^ (р, ф) = Г^г” (р) + V^w (р) $т(ф) + 22 ^^С'° (р) 8т(пф),               (2)

н=2

со(р, ф) = {0,0, coz (р, ф)}, со. (р, ф) = со(0) (р) + со0* (р) 81п(ф) + ^ со0” (р) 8т(иф).

п=2

Здесь и(р,ф) - вектор перемещения, со(р,ф) - вектор поворота.

Такая форма записи решения будет соответствовать полному отрезку ряда Фурье, если в соотношениях (2) cos( ) заменить на sin(-), a sin(-) на •- cos(-). При такой замене разрешающие системы дифференциальных уравнений относительно коэффициентов Фурье будут в точности соответствовать по виду системам, полученным ниже [4].

Основные соотношения моментной теории упругости

Приведем основные соотношения моментной теории упругости [8]: уравнения равновесия:

Va+X = 0,

(3) a⁷:E + V- p + ¥=0;

геометрические соотношения:

у= Vu -Е со,

Х = Vco;

физические уравнения:

о = 2цУ'1 + 2аУ^ + V, (у)е,                    .

И = -'ПС"' + W^Ai + РА (%)е.

С учетом соотношений (3)-(5) уравнения равновесия для вектора перемещения и и вектора поворота со примут вид

(2p+X)grad div u -(р + a)rot rot u+2arot co+ X = 0,

(2y+ P) grad div co- (Y+e) rot rot co+ 2a rot u - 4aco+Y = 0.

В приведенных выше уравнениях символом Е обозначен тензор Леви - Чивита третьего ранга, (•)^<1>) - операция симметрирования, (-)^М)- операция альтернирования, V() - набла-оператор, ДО- первый инвариант [4], X - вектор массовых сил, ¥ -вектор массовых моментов, и - вектор перемещения, со - вектор вращения, у и у -тензоры деформаций и изгиба-кручения, аир- тензоры напряжений и моментных напряжений, p, X - постоянные Ламе, а, р, у, е - физические постоянные материала в рамках моментной теории упругости.

В отличие от классической теории, тензоры у и о являются несимметричными.

В работах [12] и [13], используя условия положительности внутренней энергии.

установлены следующие неравенства:

ЗА + 2р + а > О, 2ц + а > 0, а > О,

3|3 + 2у>0, |у-е|<у + е, у + е>0.                  '

В данной работе авторами получены точные аналитические решения ряда плоских задач. Приведение этих решений к безразмерному виду позволило ввести три безразмерных величины, одна их которых зависит от характерного размера /:

a=z)                    _c=v^..             _(S)

\(а + ц)(у+Е) а у+е

Используя (7), несложно выписать неравенства, ограничивающие значения данных величин: А > О, В > 1, |С| < 1.

Будем рассматривать также среду, описываемую упрощенной теорией [8]. в которой принято, что вектор поворота удовлетворяет соотношению (Г).

Физические соотношения среды псевдокоссера:

0 = 2^+M:(y)e-^V.p,E.

p = 2^(5i +2ех(-° +р/,(х)е.

Для нахождения компонент тензоров деформаций и изгиба-кручения, как и в полной моментной постановке, используется соотношение (4). Однако, с учетом (9), уравнения равновесия для среды псевдокоссера примут иной вид, отличный от (6):

pV^zu + (ц + Л) grad div u + — (у + е) rot rot V²u -X - 0.

С точки зрения удобства анализа получаемых решений все величины приведем к безразмерному виду. Пусть / - некоторый характерный размер, который в дальнейшем будем выбирать в зависимости от геометрии задачи. м,,0);,у;,% ,oiz,p. ,A'. - безразмерные величины, которые связаны с размерными Ддр.у .у ,д .и ,Х соотношениями

Ху=-Х„. Ф. -ЦО,.            А .      (И)

Построение аналит ических решений

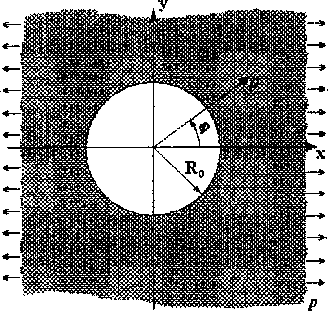
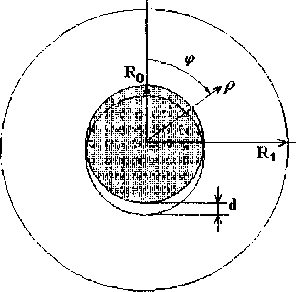
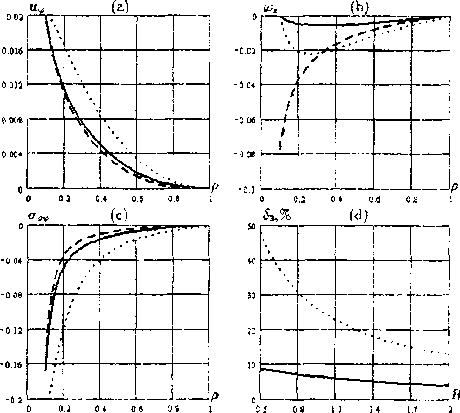
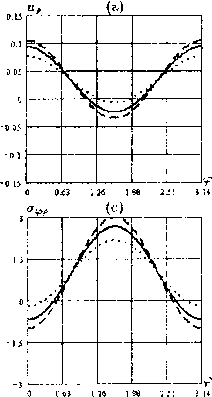
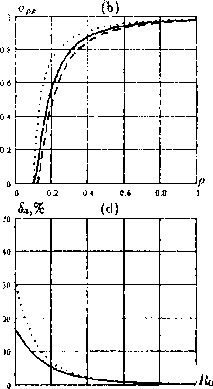
Подставляя вектор перемещений и поворота (2) в (6), получим последовательность систем дифференциальных уравнений относительно функций, представляющих собой коэффициенты Фурье. В силу того, что рассматриваемые области являются телами вращения, системы дифференциальных уравнений относительно каждой гармоники «развязаны». Следует отметить, что такая ситуация будет иметь место, если краевые условия представимы рядами, аналогичными (2).

Для коэффициентов нулевой гармоники система разрешающих уравнений имеет вид:

I и^го'- (р)+ -4-и^№ (?) - 4^⁽⁰⁾ (?) - °’

, dp"          р dp          р

■ f (Р) +                <Р) - ~4 “’"(Р) - о.

dp-        р dp       р        a + pdp vdp-         р dp         у + е         y + Etfp         (у + е)р

Для первой гармоники:

i      (р) + - — UiV1 (р) - ^-^—4U”! (Р) - ~Кт (р) - dp*         р dp (2ц + Х)р*         (2ц + Х)рс?р

—- И" (p) +--Kv* (p) - —------ V-' (p) +---:--Cr (p) - dp" p dp w (a + a)p          (p + a)p dp

3u + a+X . 2a d        _n

-  -------- U^w (p)---to¹ (p) = 0,

(p -r- a)p"          a + p dp d‘          I d m, 4ap2+y + E fb, . 2a d .

■ (p) +

—_  (p) + ----- и^w (p) = 0.

(y + E)p (Y + e)p

Для остальных гармоник:

¹ dp           p dp

ДУЛ^Л^и.-Чр)^ (2ц + Х)р         P

+ "А-о + Й A_v«_(p) - "(^"И r->(P) + ²-“ m¹"(P) = 0 (2p + X)p dp          (2p + X)p          (2p + X)p

_£_ v:^ (p)+LA_ yw (p)Hi^tl2±E±ZLA y<") (p) + dp-         P dp             (p + a)p~

_ „(«^-y^y,., ,_p| _ «№t«ip)y„_1(p) _ Д _ш(._{1(р) =}

(p + a)p dp          (p + a)p*          a + p^P d'" x 1 d ux, . 4ap2 + n-(y + e) s 2a d .

—- co(" (p) +--co ’ (p)-----4—- co1'" (p) +  --к(я- (p) + dp"        p dp           (y+e)p'           y+£<7p

+ - ²“- K^’ (p) + -3H2_u^> (p) ₌ o.

(y + E)p        (7+e)P

(14, a)

(14.6)

(14,b)

Первое уравнение системы (12) описывает решение классической задачи Ляме [4] и не связано с двумя последующими уравнениями этой системы, которые, в свою очередь, описывают задачу кручения несимметричного упругого материала. Из этого видно, что наипростейшей задачей, на которой угже проявляются моментные свойства среды, является задача кручения. При построении общих решений этих систем будем использовать известный факт о том, что частные решения соответствующих краевых задач симметричной теории являются частными решениями для краевых задач несимметричной [8].

Для U¹"⁶' (р) решение известно [4]. Решение для Р⁽⁰⁾(р) и ш⁽⁰’(р) имеет следующий вид:

_1—

	Р
-И°Чр) = С)0	п АГ У|(2^Р) - ^эМ       п , Р р 4    2       Сб 2А2   ’          ( J
	, _ с№ВЦ2Ар)+ с,0)ЖЛ^^Р) 5 2А 1 4      2л '

Можно также выписать решение для системы (13):

t/(i) (р) = СУ + ^ + С<пр2 + су ln(p) + Q1' ААМ + су -1^М, Р                            РР и'Чр) —с!" +   + су       - с”> |ш№) + ЖI + р-                              I         Зц + ?,

<                      Р                                                 J(16)

Т Ч ‘)--2Л/0(2Лр) 7 - Ч )-------+ 2ЛА„ (2Лр) ,

I Р                     J I РJ

«Пр) ₌ с_з^(|>        - су - сУ2А¹В/₁(2Ар) - су 2А’ВК (2 Ар).

ц-Х (Зц + Х)р

Здесь /„ (р) - модифицированная функция Бесселя первого рода [1], [3], в пределе при р—>^ стремящаяся к бесконечности:

v Г(£ + I)F(v + £ +1)                              '

К_п (р) - модифицированная функция Бесселя второго рода, или функция

Макдональда, в пределе при р —> °= стремящаяся к нулю:

^(P) = (-l)v+1/v(P)(C + ln(p/2)) + l^(-ir iт

НГ у Ф£2>А7у1 + уГ|                   * М где v - целое число, С - константа Эйлера (0=0,5772,..).

В выражениях (15)-(16) и далее вид частных решений, стоящих при коэффициентах Ср-СУ, соответствует симметричной теории упругости, а при СУ,СУ - несимметричной. В дальнейшем эти два частных решения мы будем называть "моментными". Проблема состоит именно в нахождении "момешных" частных решений. Подробно изложим методику их получения на примере решения системы (14) для л-й гармоники, где и > 2.

Общее решение системы уравнений (14) имеет вид

р(р) = CU. (р) + СЛ₂ (р) + С_зи_з(р) + С_Аи_д(р) + C_SU_S (р) + C₆U_b (р), (19, а) 4(р) = С,^(р) + СД₂(р) + СД₃(р) + ^^ (19,6) (®(р) = С,®! (р) + С, «₂ (р) + c₃to₃ (р) + С₄ю₄ (р) + c₅to₅ (р) + c₆to₆ (р), (19, в)

где С',(р), И(р), <о,(р), (i = l,...,6) - частные решения системы (14), а С, - произвольные постоянные, определяемые из краевых условий. Верхний индекс п здесь и далее опущен для сокращения записи. Вид частных решений, стоящих при коэффициентах С, - С₄, соответствует симметричной теории упругости:

. М      ж ^ Х(п ~ 2) + ^” " 4) -          ^ + 2) + М^' + 4)

р.»-п   р(«-1)   Хи + р(н + 2)      3        4 X« + p(«-2)

с: Х(2« - 2) + ц(4и - 4) . Х(2п + 2) + ц(4и + 4)

со (р) =----С4------------------  -р .

р” Хи + ц(ч + 2)            Хи + ц(« - 2)

Частные "моментные" решения можно отыскать в несколько этапов. На первом этапе повысим порядок, исключив из системы неизвестную функцию Г(р) и получив тем самым систему уравнений четвертого порядка. Далее, еще раз повысим порядок, исключив функцию ю(р), и получим обыкновенное дифференциальной уравнение шестого порядка относительно СДр). Потом используем процедуру понижения порядка [5] с использованием классических частных решений (20), что позволит отыскать оставшиеся "моментные" решения.

Исключим переменную И(р). Для этого продифференцируем уравнение (14, а), заменив в нем вторую производную по V значением, взятым из (14. б). Получим уравнение третьего порядка относительно Е/(р), после чего перепишем его и (14, а) следующим образом:

4 и(р)+а 4-^v^--4^^и^⁺ р" р dp        dp        р dp“

A d

р²dp

1 +4(7(р)+-— "®(р)+4о)(р),

Р'        р dp р-

я(3ц + «+ X) ... . и(ц-а + Х) d . d- _х \ d _х

—Г(Р) —= --т^(р)------Ьфр) +

(Х + 2р)р"          (X + 2|i)p dp dp р с/р

ц(2 + п‘) + со?2 + X 4+W

t/(p)-

2иа

(X -к 2ц)р

ш(р).

Представляя (21) как систему линейных алгебраических уравнений, разрешим ее огносшелыю символов И(р) и — И(р):

г(р)=w 4чи^+b^1 4-и^+м4-и<^+-'V <р • dp            dp*          dp

+ S_]5p"—to(p) + s,₆pto(p), dp

• 4-    ^p) - s_2lP²<_вд^{4 в}^4~т^u^*^b^ 4~^u^ —-^(p>+

dp          dp          dp          dp       p

+ S₂₅p4- oXp) + S₂,co(P).

dp

Для примера приведем вид констант в соотношении для ^(р) :

, ₌__(Ц + а)(Р - а + ^)

• ¹¹    и(иХ 4 2а - па 4 2ц 4 пц)(иХ - 2а - по. - 2ц 4 пц)

, _              2(ц + а)(а - Зц - 2Х)_____________

• ¹²    п^пХ 4 2а - на 4 2ц 4 пр\пХ - 2а - на - 2ц + пц) ’

; _ и2Х2 4 Хц 4 Ха-Зп2Ха4 п2Хц4 а2-2п2ац4 Зц2 4 2п2а2 4 4ац

• ¹³          п(.пХ 4 2а - па + 2ц + пц)(пХ — 2а - «а - 2ц + пц)

, _         (Зц -г а + Х)(ц 4 а 4 2п2а - п2X)_________ п^пХ 4- 2а — па + 2ц + пц)(пХ - 2а - па - 2ц 4 пц) ’

• ,    _                2а(а - ц - X)

• ⁵    (пХ + 2а - па + 2ц + иц)(пХ - 2а - па - 2ц + пц) ’

; _                      4а(ц 4- а)

• ¹⁶    (jtX 4 2а - па 4 2ц 4 пц)(пХ - 2а - па - 2ц 4 пц)

Дважды дифференцируем (14, а), каждый раз заменяя выражения для —-Pidl dp"

— (z(p), ^(p), —уоХр) на значения, взятые из (14,б)-(14,в) и (22), в ре ;<лы.- с dp           dp получим уравнение четвертого порядка относительно U. Добавляя к нему уравнение (14, в), в которое также подставлены выражения (22), получим систему однородных линейных дифференциальных уравнений четвертого порядка с двумя неизвестными функциями:

У⁴ ,.    6 d³ 5-2

— L'(P) = —— Рф)---2 ар        Р dp         р

^-1_Щр)-

Р'

2па

р2

d2

СЧР) +

1 + 2п² d

(a + ц)р dp.

®(р) -

Р"

2па

dp

G4P) -

d

(а + ц)р²dp

А_?(й(р) = -| D_lp + -l-^-oXp)-| ^-^\to(p)-D₃p² 4^^u(.pV dp-       ( p)dp ( P'V          dp

.   - AP ^(P) - d₅ U(P) - " ^(P).

I         dp"           dp p

Коэффициенты данных уравнений определяются соотношениями:

\   _                      8а2(2ц + Х)

, . 2л³а . , со(р) + ---—--(o(p),

(а + ц)р^

\D.

(у + е)(иХ + 2а — па + 2ц + лц)(иХ - 2а - па — 2ц + иц) ’ 4а(и²ц² - 4ц² -- 4ац + 2и²Хц - п"аХ + п"Х" - лгац)

D

(у + е)(иX + 2а - па + 2ц + пц)(иХ - 2а - па - 2ц + пр) ’ 4а(а + ц)(2ц + X)

D,

D,

n(y + e)(nX + 2a - па + 2ц + нц)(иХ - 2a - па - 2ц + иц)' 2а(2ц + X)(n²X + 8ц + и²ц - и²а + 8а)

и(у + Е)(пХ + 2а - па + 2ц + пр)(пХ - 2а - па - 2ц + иц) ’ 2а(2ц + Х)(Зи²Х + 2ц + л²ц - 5п²а - 2а)

л(у + e)(nX + 2а - па + 2ц - пр\пХ - 2а - па - 2ц + иц)

i 2а(и - V)(n + 1)(2ц + Х)(п²Х - 2ц + и²ц - п"а - 2а)

[ ⁶ п)^ + е)(пХ + 2а - па + 2ц + лцХлХ - 2а - па - 2ц + иц)

Еще раз выполним процедуру повышения порядка, исключив из (23) функцию 0)(р) и сведя его к уравнению шестого порядка. Процедура аналогична описанной ранее, поэтому приведем только результат:

«ХР> = Гр^:-ттГ(р) + ^Pvr^CP) + (Г + Лр²) "7Т^у (р) + dp           dp        ^х         ’ dp

+ F4pj™L4p) + ^ + F2^(7(p) + f4 + ^|[7

V Р )dp (р )dp VP" P )

<24)

Уравнение шестого порядка: d'         9 d^s        (

~С(р) + - — П(р)- G + 3 dp'       р dp        (

(GQn--5) Н-п1*)

п" -4) d^A        (6G . п² 4-d³ ,

—— ту^Р)- —+ 6-^- ——П(р) + р ) dp V Р Р ИР"

Р"

-G(n - I)² (и + I)²

Р4

P4

jyr^PH

ИР

\G)2nHY) п2-п4—3

Р3

Р

d dp

Р

_G _ 4ац (р + а)(у+е)'

Вопрос о существовании решения данного уравнения разрешается теоремой [51: если коэффициенты уравнения (25) непрерывны в интервале (а,Ь), то существует фундаментальная система решений, определенных в этом интервале.

Коэффициенты при производных в левой части уравнения, содержащие независимую переменную, имеют вид двучленов по степеням этой переменной, причем для каждого коэффициента сумма абсолютных значений младшей степени и порядка производной не превышает порядок уравнения. Это означает, что частное решение представимо в виде обобщенного ряда по независимой переменной:

0>) = £s,p^-

Характеристическое уравнение относительного параметра ц имеет вид

(q - п - 1)(^ + и + 1)(^ - и + \)(q ап- 1)(с/ An- 3\q - и - 3) = 0.

Известно [5], что для максимального значения параметра q можно постротъ частное решение в виде обобщенного ряда (26). Для остальных значений этого параметра это также возможно, если эти значения не кратны максимальному и не кратны между собой. Кроме этого, такое представление частных решений не всегда возможно, если разница между значениями параметров целочисленна. В нашем случае целочисленная разница значений дает нам кратность корней характеристического уравнения для некоторых п. Поэтому для отыскания "моментных" частных решений воспользуемся методом понижения порядка уравнения (25), последовательно применяя подстановки, основанные на классических решениях (20) [5]:

6/(р) = (/,(р)- \H(p)dp, Я (р) = 4Г777т1   ' =

J                               (7,(Р) )

щр)=я,(р)-Jj(pXp,

Лр) = Л(р)рХрШ цр)=д (р) ■ fww

В результате получим уравнение второго порядка

^² л 5 + 2п d , 9 + 6n-Gp²

—— Л/(р)-----—л/(р)я--;----Л/(р)-О.                (28)

dp          р dp           р"

Данное уравнение имеет два частных решения [3]:

=                                      rQ)

[^(pW^Jv'Gp).

Осуществив преобразования (27) в обратном порядке, получим искомые "моментные" частные решения:

u_s (р) = p⁴/,(Vop),

[U6(p) = p-1K„(VGp).

Подставляя (30) в (19, а), получим частные "моментные" решения для радиальной компоненты вектора перемещения. Далее, используя (24), определим "моментные" решения для вектора поворота. Зная их и используя (22,а), несложно отыскать частные решения для азимутальной компоненты вектора перемещения.

Окончательно запишем решение в безразмерной форме. Для этого в качестве характерного размера выберем некоторый радиус Л] и воспользуемся ранее введенными (8) безразмерными величинами А, В, а также связью безразмерных и размерных характеристик напряженно-деформированного состояния (И). Дополнительно обезразмерим константы.

Все это позволяет выписать безразмерный вид общего решения в явной форме:

+ -а_/я(2ИР)+-^-к;(2М р

С^ Х(л - 2) + ц(и - 4)

рн) р(„-о Хи + ц(н + 2)

_    Х(^2) + ц(л + 4) _р(„_+п ^ Г JI ₍₂^_р) _ 2А , _{(2 4р)})

Л/г + ц(« — 2)               ( р            п)

+ С^|1к„(2Лр) + —K„_,(2.4p) ,

₍       №-2) + ц(4и-4)_с,„, Л(2л + 2) + р.(4и + 4)

р”     Хп + ц(л + 2)       ⁴Хп + ц(н - 2)

• - СГ» =^-1„ (2 Ар) - С^ ^-К„(2Ар). пп

Константы при частных решениях в соотношениях (15), (16) и (31) определяются из краевых условий соответствующих задач.

Соотношения (15), (16) и (31) будут являться также и решениями уравнения (10), описывающего краевую задачу для среды псевдокоссера, если В = 1 (8), что соответствует предельной ситуации при а ->. Подробное доказательство этого утверждения выходит за рамки данной работы. Следует отметить, что эго можно доказать, также используя вышеописанную методику.

Анализ решений некоторых конкретных задач

В качестве конкретных задач рассмотрим две:

• 1.    Задачу о деформировании кольца (цилиндра), жестко закрепленного по внешнему контуру р = 7?_t (рис. I). Деформирование осуществляется за счет жесткого смешения внутреннего контура р = R_u на величину d. Решение этой задачи получится, если в рядах (2) удержать одно слагаемое при /7=1. Для этой задачи на рис. 2

• 2.    Задачу Кирша об одностороннем растяжении пластины, ослабленной круговым отверстием. Края кругового отверстия в данной задаче свободны от внешних напряжений, а на бесконечности действует растягивающее усилие постоянной интенсивностир в направлении оси Ох (рис. 3). Решение этой задачи получится, если в рядах (2) удержать слагаемые при л = 0 и и = 2 .

  
  
  

Построение и анализ некоторых точных аналитических решений представлены распределения по безразмерной радиальной координате р безразмерных компонент:

• а)    вектора угловых перемещений и;

• Ь)    вектора поворота сн₂ относительно оси z;

• с)    тензора напряжений ст.

Радиус внутреннего контура R,, =0,1. относительное смещение d -• 0,02 .

Рис. 1. Деформирование кольца, жестко закрепленного по внешнему контуру

Рис. 2. Распределения безразмерных компонент по безразмерной координате р для задачи 1

Рис. 3. Одностороннее растяжение пластины, ослабленной круговым отверстием

Рис.4. Распределения безразмерных компонент по безразмерной координате р для задачи 2

Впервые, в рамках классической теории упругости, эта задача была решена Киршем (Kirsh), позднее, несколько иным путем, Н.И, Мусхелишвили [7]. Обобщение этой задачи на случай среды псевдокоссера можно найти в работе R.D. Mindlin [14]. В.А. Пальмовым [10] была найдена концентрация напряжений вблизи кругового отверстия в рамках несимметричной теории упругости.

Следует отметить, что решение, приведенное в [10], не позволяет в полной мере проанализировать напряженно-деформированное состояние в окрестности кругового отверстия, в частности, характеризовать степень искажения отверстия при деформировании.

• Для задачи Кирша на рис.4 представлены следующие зависимости:

• а)    радиальной компоненты и вектора перемещения от координаты ф для р = ^о;

• Ь)    компоненты о _рр тензора напряжений от координаты р для ф = 0;

• с)    компоненты a_w тензора напряжений от координаты <р дляр = R^ .

Радиус внутреннего контура = 0,1.

Все графические зависимости соответствуют следующим значениям материальных констант: а-0,2, у = € = 0,01, ц = 1, ?^ = 1,5. Сплошной линией обозначены графики, соответствующие среде Коссера, точечной - среде псевдокоссера. пунктирной - симметричной среде.

Полученные решения позволяют провести сравнения напряженно-деформированного состояния на различных границах рассмотренных областей в рамках среды Коссера, среды псевдокоссера и симметричной среды. Акцент в этом сравнении сделаем на возможность использования полученных решений с точки зрения возможности реализации эксперимента и его интерпретации.

Графические зависимости, представленные на графиках, позволяют сделать вывод о том, что в качестве экспериментально измеряемой макровеличины можно выбрать: для первой задачи осевую силу реакции внутреннего контура

F_y = J (°рф№ > Ф) ^8т(Ф) ⁺ °РР № ’ Ф) ^С°8(Ф)) М^ .

для второй - макровеличину, характеризующую степень искажения контура кругового отверстия от действия одноосной нагрузки,

D =

^Р(^,0)

«р№,л/2)

Относительные параметры, характеризующие степень отличия моментных решений от классических по введенным макровеличинам, имеют вид: для задачи о деформировании плоского кольца

100%,

для задачи Кирша

D-D*

D*

■100%

Графические зависимости введенных относительных параметров от соответствующих характерных размеров приведены на рис. 2, d и 4, d. Из сравнения этих графиков видно, что:

• 1)    все относительные параметры возрастают по мере уменьшения характерного размера;

• 2)    наибольшая степень возрастания имеет место для величины б., соответствующей задаче Кирша.

Выводы

Предложен подход к построению точных аналитических решений некоторых плоских краевых задач в рамках несимметричной теории упругости (для сред Коссера и псевдокоссера). С использованием данного подхода получены решения двух задач, которые позволили:

• 1)    осуществить сравнения описываемых ими напряженно-деформированных состояний, а также сравнить с ними напряженно-деформированные состояния, описываемые классическими решениями;

• 2)    определить возможные экспериментально измеряемые макровеличины с целью установления степени их отклика на моментное описание поведения материала;

• 3)    ввести относительные параметры, характеризующие степень отличия моментных решений от классических по соответствующим макровеличинам;

• 4)    получить графические зависимости относительных параметров от соответствующих характерных размеров (масштабов), а из их сравнительного анализа установить наиболее интересные с точки зрения возможных схем постановки и реализации эксперимента.

Качественный и численный анализ аналитических решений, полученных выше, а также зависимостей, представленных на рис. 3-4, позволяет сделать ряд выводов:

• 1.    Безразмерная форма записи полученных аналитических решений позволила наглядно установить принципиальное различие безразмерных моментного и классического решений. А именно, безразмерное моментное решение зависит от характерного размера, а классическое - нет.

• 2.    Анализ полученных решений позволил установить, что в качестве возможной экспериментально измеряемой величины можно использовать параметр D из решения задачи Кирша, характеризующий степень искажения кругового отверстия, так как эта величина в значительной степени откликается на "моментное" описание материала.

• 3.    Можно определить влияние материальных констант на соотношение классического и несимметричного решений, а также для среды псевдокоссера. Классическое решение является одной предельной ситуацией для несимметричного (при а—>0), а псевдокоссера - другой (а— >°°). Различие же классического решения и решения псевдокоссера определяется величиной У + Е.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект 99-01-00240).