Построение и исследование корректности математической модели транспорта и осаждения взвесей с учетом изменения рельефа дна

Образец для цитирования: Сухинов, А. И. Построение и исследование корректности математической модели транспорта и осаждения взвесей с учетом изменения рельефа дна / А. И. Сухинов, В. В. Сидорякина // Вестник Дон. гос. техн. ун-та. — 2018. — Т. 18, № 4. — С.350-361.

Введение. Среди факторов, определяющих комплексное развитие исследований прибрежных территорий, большое значение принадлежит охране водной среды [1-2]. Устранение последствий естественных процессов, таких как загрязнение, заиление и истощение акваторий приводит к необходимости изучения всех аспектов, влияющих на изменение прибрежных акваторий. Поддержание водных объектов в надлежащем состоянии и своевременное вмешательство в режим его функционирования напрямую связано с увеличением портовых мощностей и обеспечением эффективного развития прибрежной инфраструктуры (обеспечение подхода к причалам судов с низкой посадкой, очистка от ила и водной растительности прибрежной полосы и пр.) [3-5]. Как правило, проведение исследований в данной области требует построения математических моделей, максимально приближенных к реальным процессам [6-11].

В работе рассматривается непрерывная математическая модель, описывающая пространственнотрехмерные процессы, связанные с транспортом и гравитационным осаждением взвесей в водной среде с изменяющимся рельефом дна. Эта модель учитывает микротурбулентую диффузию и адвективный перенос взвесей, действие на частицы взвеси силы тяжести, наличие дна и свободной поверхности, изменение рельефа дна. Модель транспорта взвеси позволяет проводить исследования гидрофизических процессов водных систем, осуществлять прогноз динамики изменения донной поверхности на основе описания процессов подъема, переноса, осаждения, изменения концентрации взвеси [12-13]. Доказана единственность решения соответствующей начально-краевой задачи и получена априорная оценка нормы решения в зависимости от интегральных оценок правой части, граничных условий и начального условия.

Материалы и методы. Непрерывная 3D модель диффузии-конвекции взвеси и соответствующая ей начально-краевая задача. Рассмотрим непрерывную математическую модель распространения взвеси в водной среде, учитывающую диффузию и конвекцию взвеси, действие на взвеси силы тяжести, наличие дна и свободной поверхности. Будем использовать прямоугольную декартовую систему координат Oxyz , где ось Ох проходит по невозмущенной водной поверхности и направлена в сторону моря, ось Оz направлена вертикально вниз. Пусть h = H +ƞ — общая глубина акватории, м; H — глубина при невозмущенной поверхности водоема,

м; ƞ — возвышение свободной поверхности относительно геоида (уровня моря), м (рис. 1).

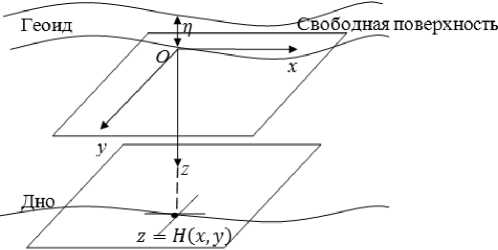
Рис. 1. Введение системы координат Oxyz

Механика

Пусть в замыкании области G = { 0 < x <  L_x ,0 <  y <  L y ,0 <  z < H ( x , y ) } находятся частицы взвеси, которые в точке ( x , y , z ) и в момент времени t имеют концентрацию c = c ( x , y , z , t ) , мг/л; t — временная переменная, сек. Также далее будем использовать обозначение L = max H ( x , y ) .

z 0< x < L x , 0< y < L_y

Поведение частиц взвеси будет описано следующей системой уравнений:

<

d c	d ( uc )	d ( vc )
+	+
d t	d x	d y
d H	8
-------:	=--wc ,
a t	p g

^d ( ( w + w g ) c )      Г₉ ² c   _б ² c \   ₅ /    _d c x

+-----я------= ^H h I 7T + 7T l + 7-| ^H v T~ l + F ,

оz          V dx   dy J  оz V  dz J где u, v, w — компоненты вектора U скорости движения жидкости, м/сек; wg — гидравлическая крупность или скорость осаждения частиц, м/сек; цh, цv — коэффициенты горизонтальной и вертикальной турбулентной диффузии частиц соответственно, м2/сек; F — мощность источников частиц; 8 — пористость донных материалов.

Слагаемые в левой части (кроме производной по времени) первого уравнения системы (1) описывают адвективный перенос частиц, обусловленный инерционным движением водной среды, а также осаждение под действием силы тяжести. Слагаемые в правой части описывают диффузию взвеси. Коэффициент вертикальной диффузии выбран отличным от коэффициента горизонтальной диффузии в связи с тем, что эффект различия этих коэффициентов часто наблюдается в различных средах и может быть вызван различными факторами.

В качестве области G рассматриваем «скошенный» к берегу «параллелепипед» ABCDA1OC1 D1, верх нее основание A OC1 D1 которого лежит на свободной поверхности (z = 0), а нижним основанием ABCD является часть поверхности дна (z = H(x, y)). Пусть S — поверхность G , n — внешняя нормаль к поверхности «скошенного параллелепипеда». Будем считать заданной U* — скорость движения жидкости на боковых по- верхностях G . В совокупности с граничными условиями первого рода для функции концентрации частиц это позволяет определять потоки взвешенного вещества как по направлению к берегу, так и вдоль берега (рис. 2).

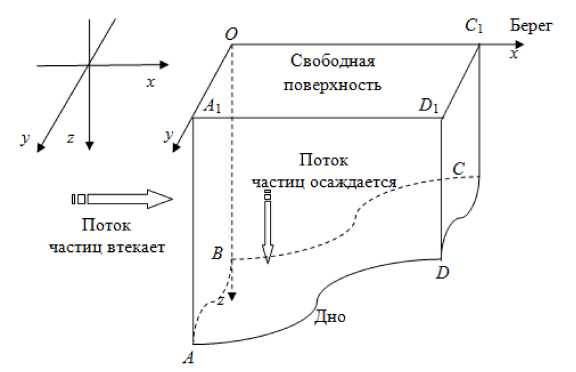
Рис. 2. Область решения задачи транспорта взвеси

Добавим к системе (1) начальные и граничные условия (предполагая, что осаждение частиц на дно необратимо).

В качестве начальных условий при времени t = 0 принимаем c (x, y, z,0) = c0 (x, y, z) ;(2)

H (x, y,0) = H0 (x, y).(3)

Граничные условия задаем на гранях ABCDA 1 OC 1 D 1 (задаем потоки взвесей как по направлению к берегу, так и вдоль берега):

— на гранях  S1 = AA1OB (x = 0,0 < y < Ly,  0 < z < Lz)  ,  S2 = AA1 D1 D (y = Ly, 0 < x < Lx, 0 < z < Lz)

S ₃ = BOC 1 C ( y = 0, 0 <  x <  L_x , 0 <  z <  L_z )

c = c*, где c* = c* (x, y, z, t), t e[0, T];(4

— на гранях S ₄ = DD 1 C 1 C ( x = L_x , 0 <  y <  L y , 0 <  z <  L_z ) и S ₅ = A₁OC₁D₁ ( z = 0,0 <  x <  L x , 0 <  y <  L_y )

c = 0;(5

— на поверхности S ₆ = ABCD ( z = H ( x, y, t ) , 0 <  x <  L x , 0 <  y <  L_y )

д c    w g       д cw

— =--- c или — =-- dn    pv        дzp

Граничное условие (5) имеет место при относительно небольших уклонах дна:

max

S 6

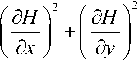
«: 1.

Следующее условие невырожденности области решения задаем для всех (x, y, t) при которых постав лена начально-краевая задача:

H ( x , y , t ) > h₀ = const >  0,    0 <  t <  T .    (7)

При исследовании объединенных моделей транспорта наносов и взвесей возможно увеличение концентрации взвешенных частиц в придонном слое за счет подъема частиц донных отложений при превышении сдвигового напряжения некоторого критического значения [13-16]. Тогда вместо граничного условия (6) будем рассматривать граничное условие вида дc                     „

— = a c , а = const >  0. (8) д z

Линеаризация начально-краевой задачи транспорта и осаждения взвесей. Для того чтобы создать линеаризованную модель на временном отрезке 0 <  t <  T построим равномерную сетку ®_т с шагом т, т. е. множество точек ш_т = { t n = n т , n = 0,1,..., N , N т = T } .

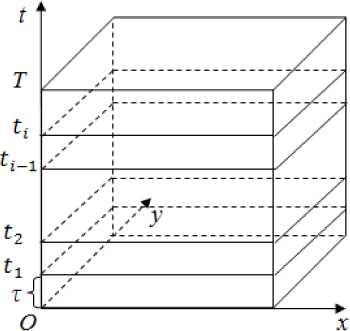
Рис. 3. Построение временной сетки

Функции c ⁽ n ) ( x , y , z , t n _1 ) и H ⁽ n ) ( x , y , t n _1 ) определяем на каждом шаге временной сетки ю_т. Если n = 1, то в качестве c ^{( 1 )} ( x , y , z , 1 ₀ ) , H ^{( 1 )} ( x , y , 1 ₀ ) достаточно взять функции начального условия, т. е. c ^{( 1 )} ( x , y , z ,0 ) = c ₀ ( x , y , z ) , H ^( x , y , 1 ₀ ) = H ₀ ( x , y ) соответственно. Если же n = 2,..., N , то функции c ^{( n} ) ( x , y , z , t_n _1 ) = c ^{( n - 1 )} ( x , y , z , t_n _1 ) предполагаются известными, поскольку предполагается решенной задача (1)-(6) для предыдущего временного промежутка t _n_ ₂ <  t <  t _n _1 .

Систему (1) на промежутке t _n _1 <  t <  t _n запишем в виде:

д _c ^{( n} ) д ( uc ^{( n} ) ) д ( vc ^{( n} ) ) д ( ( --+ —--- + —--- + ——

<

д t д H ^{( n} )

д t

д x

8 < — w^c p g

^д y

.⁽ n )

w + w g ) c ^{( n} ) )

:---------------= Рл дz           h

Гд ² c ^{( n} ) д ² c ^{( n} H

+^-

^ д x д y J

д д z

д c ^{( n} ))   _

Р v ^" + F , д z J

Механика

и дополним ее начальными условиями:

c ^{( 1 )} ( x , У , z , t о ) = c о ( x , У , z ) , c ⁽ n ) ( x , У , z , t n - 1 ) = c ⁽ n ^{- 1 )} ( x , У , z , t n - 1 ) , n = 2,..., N. (10)

H ^{( 1 )} ( x , У , t о ) = H о ( x , У ) , H ⁽ n ) ( x , У , t n - 1 ) = H ^{( n - 1 )} ( x , У , t n - 1 ) , n = 2,..., N .                       (11)

Граничные условия (4)-(6) предполагаются выполненными для всех промежутков времени t n 1 <  t <  t n .

Определив функцию c(n)(x, y, z, tnч ) = c(n-1) (x, y, z, tn_,) на временном промежутке tn_, < t < tn, можно найти функцию H(n)(x, y, tn_1). С этой целью проинтегрируем обе части второго уравнения системы (9) по пе ременной tn _1 < t < tn. Получим tn-1

Из равенства (12) нетрудно получить

H ) д 1

£ dt = — w„

P g

tn

J c ^{( n} ) dt .

t n - 1

N ^t n

H ( ⁿ ) = h ( ^{n - 1} ) -^£ w g J J c ( ⁿ ) dt .

P      n =1

t n - 1

Введем       на       каждом

временном       шаге

t

область

G n -1 = { 0 <  x <  L x , 0 <  y <  L y , 0 <  z <  H^{n 1} ( x , y , t n _, ) } .

Имеем цепочку линейных начально-краевых задач для каждого временного слоя, где для промежутка

t n _ч<  t <  t n рассматривается система вида

д _c ( ⁿ )    д ( uc ^{( n} ) )    д ( vc ^{( n} ) )    д ( ( w + w g ) c ^{( n} ) )

--+ —--- + —--- + —-------- = ц д t      дx        ду            дz

< ( х , y , z ) е G n - 1 , G n - 1 = { ⁰ <  ^x <  L x , ⁰ <  У <  L y ,

H ( ⁿ ) = h ( ^{n - 1} ) _ ^£ w N f c ( ⁿ ) dt , n = 1,2,..., N . ^g

2 ( n ) 22. ( n ) ( n )

I д c ^! д c 'I д I д c 'I ^ д x ² д y ² J д z ^^ v д z J 0 <  z <  H^{n - 1} ( x , y , t n - 1 ) } ,

с начальными условиями:

c ⁽ n ) ( x , У , z , t n - 1 ) = c ⁽ " 1 ) ( x , y , z , t n - 1 ) , ^{H (} n ) ( x , У , t n - 1 ) = ^{H (} n ^{- 1 )} ( x , У , t n - 1 ) .

Отметим, что на каждом временном шаге граничные поверхности будут меняться (исключение грань

S ₅). Рассматривая временной промежуток t_n _, <  t <  t_n , осуществляем задание граничных условий на гранях об

ласти G_n - 1

— на гранях S 1, n - , ( x = 0, 0 <  y <  L y , 0 <  z <  H ^{( n 1 )} ( 0, y , t n - , ) ) S 2, n - 1 ( y = L y , 0 <  x <  L x , 0 <  z <  H ^{( n} 1 ) ( x , L y , t n - 1 ) )

и S 3, n - 1 ( У = 0, 0 <  x <  L x , 0 <  z <  H ^{( n} 1 ) ( x ,0, t n - 1 ) )

c ^{( n} ) = c * , где c * = c * ( x , y , z , t ) , t e [ t n - 1 , t n ] ;

— на гранях s4,n-1 (x = Lx, 0 < y < Ly,  0 < z < H(n-1) (Lx, y, tn-1))

и S 5, n -1 ( z = 0, 0 <  x <  L x ,  0 <  y <  L y ) - A 1 OC 1 D 1

c ^{( n} ) = 0 ;

— на поверхности S 6, n - 1 ( z = H ^{( n} 1 ) ( x , y , t n - 1 ) , 0 <  x <  L x , 0 <  y <  L y )

д c ^{( n} )

—

д n

w _{g  n}

— c ( ) или

Ц v

д c ^{( n} )

д z

—

w L c ( n ) Ц v

.

Граничное условие (8) заменится на следующее

( n ) д c ( )     . ( n )

-----= a c' ) , а = const >  0.

д z

Таким образом, предполагается, что рельеф дна в пределах данного временного шага при расчете распределения концентраций взвешенного вещества не меняется и берется из предыдущего временного слоя. В первую очередь на данном временном шаге tn 1 < t < tn решается начально-краевая задача для уравнения кон векции-диффузии (14) с зафиксированной функцией рельефа дна H(n 1), а уже затем выполняется обновление (пересчет) функции рельефа H(n) в соответствии с равенством (15). Определение условий существования, единственности и непрерывной зависимости решения от входных данных задачи проводится на фиксированном временном слое в этих предположениях и при условии выполнения условия (7).

Авторы не планируют исследовать в данной работе существование решений начально -краевых задач (14)-(20) и (14)-(19), (21). Вопросы существования решений начально-краевых задач для уравнений параболического типа с младшими производными (уравнений диффузии-конвекции) рассмотрены, например, в монографиях [17-18].

Результаты исследования. Исследование единственности решения начально-краевой задачи транспорта взвеси.

Рассмотрим начально-краевую задачу (14)-(20), сформулированную для произвольного временного слоя t n —1 <  t <  t n .

Умножим левую и правую часть уравнения (14) на функцию c ^{( n} ) и получим:

d c ^{( n} )    d ( uc ^{( n} ) ) d ( vc ^{( n} ) ) d ( ( w + w g ) c ^{( n} ) )

d t       d x        д y            d z

( n )

= h h c

fd ² c ^{( n} ) d ² c ^{( n} H

-71-⁺ d x     d y

X

_ (n ) ⁵

+ c^{v 7}

d z

h

d c ^{( n} ) ' a z ,

+ c ^{( n} ) F .(22)

Левая часть равенства (22) может быть преобразована следующим образом:

( n ) d c ^{( n} )      ( „ )

c       + c д t

d ( uc ^{( n} ) ) d ( vc ^{( n} ) ) d ( ( w + w g d x        д y            d z

1 d(c(n))

=¹ -^--Г +1 div

2 d t 2

) c ^{( n} > ) ]     1 d ( c ^{( n} ) ) ²

2    d t

+ c ^{( n} ) div ( c ^{( n} ) U ) =

где U = || u , v , w + w_g ||

С учетом (23) уравнение (22) запишется в виде

1 *7

2 d t

+ div

( n )

= h h c

fd ² c ⁽ n )    d ² c ⁽ n П

'

V d x      д У   )

+ c

.(n И dz

d c ^{( n} ) )

hv dz

+ c ^{( n} ) F .

Затем обе части уравнения (24) проинтегрируем по времени на интервале tn_1 < t < tn и, после этого — по пространственным переменным в области Gn_1. В первом слагаемом порядок интегрирования изменён в си лу теоремы Фубини [19]. Получим

ITT 1J

G n - 1 ² t n - 1

= I JIT c- ' h h t n - 1 V G n - 1

V

Г

V

a ( c ⁽ n Ч² )

-^--Гdt dG at           "

d2 c(n) d2 c(n >) "^+^t- ax     ay j tn Г

+ tn

tn

J 1 ITT div (( c'-^^U')

t n - 1 V G n - 1

t n - 1

tn*

d^G .-1 ^dl + T TTT c "x 7        t n - 1 V ^G n - 1

T JJ _T c ^{( n} ) FdG_n _, dt .

t n - 1

V ^g-

^ dG .._,

dt =

7 dc(n)) u ---- dG, v dz ’

^ dt +

Первое слагаемое из левой части равенства (25), очевидно, равно tn

TTT1 T

G n - 1 ² t n - 1

d ( c ⁽ n ) ) ²

dt d t

dG n -1

= Ш ¹ ( ( c⁽ n ) ) ( x ^, y ^{, z ,} t n ) - ( c ⁽ n ) ) ( x , y , ^z , t n -1 ) ) ^dG n -1 .

G n -1     ^X                                                                          '

Далее обратимся к преобразованию второго слагаемого левой части равенства (25). С учетом формулы Остроградского-Гаусса и граничных условий (18)-(20) его можно записать в виде [20]:

Механика

J |1JJJ div ((c"’)’ U)

tn

t n - 1

t n

G n - 1

tn

J JJ ( c ■) 2 ( U 'n )

t n - 1 V S 3, n - 1

1 ^tn

у

dG

dt =

dxdz dt +

" f                             J          t n.

2 J л (c*) (U*, n)dydz dt+2 J jj tn-1 \ S1, n-1                                     J             tn-1 \S6, n-1

• 1    J | iJ ( c ' ) ²     . n )

• ²    t n -1   "

V ^S 2, n - 1

1 ^tn

t n

J c2 wdxdy dt + g

У

dxdz dt = — J JJ ( c *) udydz dt - ² L

J

tn

V S 1, n - 1

1 ^tn

л

1 ⁿ 2 1 ⁿ 2 1 n 2

— J JJ ( c ) vdxdz dt + ^_ J JJ ( c ) vdxdz dt + — J I JJ ( c ^{( n} ) ) w_gdxdy I dt .

2 t_n

t n - 1

V S 3, n - 1

2 _t

t n - 1

V S 2, n - 1

2 t_n

t n - 1

V S 6, n - 1

У

где U * — известная скорость водной среды на гранях, где заданы граничные условия первого рода; фактически

это все боковые грани, кроме S 4, _n 1 и верхней крышки S 5, _n 1 , на которых концентрация взвеси равна нулю, по-

тому и потоки через них равны нулю.

Обратимся к преобразованию правой части равенства (25). Имеет место равенство

JJJ c "

G n - 1 L

Ц h^T д x

5 f 5 c ^{( n} ) J

5 x

+ Ц h -

д f 5 c ^{( n} ) J

d y V d y

5 д z

d c ⁽ n >Yf|

Ц ■ дz

dG n -1 =

^{JJJ Ц} h 5 x ¹ c

G n

^Tn -1 _

, . , 5 c:: д x

.    5   (

+ц h^ ^c

5 y V

₍ .

—

JJJ ц h

G n - 1

Пусть Q = { Q x , Q y , Q z } = j ц „ c* n )

Гаусса имеем:

шГц ■ If c ^д x v

, ( n )S c y_)

G n

^{д x} J

d c ^{( n} ) 5 x

J ²

+ Ц h

д c ⁽ n )

^д y J

■  +Ц v

д д z

( n )

^{c (}4

5 c ⁽ n ) д z

5 c ^{( n} ) д z

dG n -1 .

^dG n -1 ^-

д c ⁽ n )        r n ) д c ⁽ n )    r n)     5 c ⁽ n ) 1

----, ц_н cⁿ⁾ ----, c ^ ^;ц ---- >. Тогда в силу теоремы Остроградского- d x     h     д y         v  д z  I

5f ( + ц h    c дy V

.< - >*^

д

. ( ⁿ )

я ⁺^ c ⁽⁾ ц v д y J  д z

V

n -1                                          Z                      X                     /               x

= JJ Q y dxdz + JJ Q x dydz + JJ Q y dxdz + JJ Q x dydz +

/                         n - 1

JJ Q z dxdy + JJ Q z dxdy =

S 2, n - 1                        S 4, n - 1                        S 3, n - 1                        S 1, n - 1                        S 6, n - 1                        S 5, n - 1

= JJ Q y dxdz + JJ Q y dxdz + JJ Q x dydz + JJ Q z dxdy .

S 2, n - 1

S 6, n - 1

Преобразуя каждое слагаемое из правой части (29) с учетом условий на границе (18)-(20), получаем

я^ ц h I I c

G n - 1

₍ . >&» J

5 x  ,

д

+ ц h^- c

8 y

д ( n ) A . ( n ) ^д c

5 c ⁽ " > )"

*

= JJ ^c *ц h ^T dxdz ⁺ JJ

S 2, n - 1             ^{д y}                S 3, n - 1 1

^ *

*   д c c Ц h^T

д f ( n )     5 c ⁽ n )

+ — c У v— dG, дz V       дz J

^Tn -1

dxdz + JJ c *ц _h^—dydz - JJ w ( c ^{( n} ) ) dxdy . д x               g

S 1, n - 1                                        S 6, n -1

С учетом (26), (28), (29) и (30) равенство (25) принимает вид

—

tn

*

2 jjj ( c⁽ n ) ) ^{2 (} x , y , z , t n ) dG n -1 - J jj 1 2 ⁽ c *^{) 2} u ⁺ c ‘ц h ^ x

/

G n - 1

t n

J JJ I 1 ( c •)

t *s \ ^

- n - 1 \ S 3, n - 1 ^v

t n - 1 V S 1, n - 1

t n - 1

у

V S 3, n - 1

dydz dt

—

J dxdz dt +

J

5c(") J 2' , дz J , J dt.

J

\

n 2

⁺ 2 J JJ w g ^{( c} ( n ) ) ^{dxdy dt +}

t n - 1

V S 6, n - 1

J

t n

J JJJ tn-1 Gn-1

д е ^{( n} ) д x

J ²

■  +ц h

f 5 c ⁽ " )

v ^д y

Г

+ Ц

dG n -1

dt =

tn

= 1 JJJ( е^, " ' ) ² ( x , y , z , t - -1 ) ^dG - -1 + J JJJ c'^dG

²                                             t n V G n -

G n - 1

n -1

Тождество (31) будет основным при исследовании единственности и получения априорной оценки нормы решения начально-краевой задачи (14)-(20). В случае замены граничного условия (20) на граничное условие (21), квадратичный функционал (31) изменяется следующим образом:

/

—

+J JJ

t n — 1

V S 6, n — 1

tn

*

д c

2 JJJ( ^c( n ) ) 2 ^{( x} • у • ^z • t n ) ^dG n —1 ^— J JJ 1 2 ^{( c} *^{) 2} u ^{+ c} * Ц h “ x ^G n — 1                                                t n — 1 V ^S 1

G n

tn

J UI 1 ( c •)

*n — 1 V S 3, n — 1 V ²

* 1, n — 1

t n — 1

w

2 ^g

—

dydz dt

—

²       .    8 c

I v + c ц h —

ац _v I ( c ( ⁿ ) ) dxdy dt + J

t n

J JJf

t n — 1

G n

t n — 1

S 2

8 c ^{( n} ) д x

V

■  +ц h

*²      *. ^{8 c} L j .

v — c ll--- dxdz dt + h ЗУ J    J

д c ⁽ n )

V

+ц

' д c ⁽ n ) ' . д z ,

dG n —1

dt =

1 dt .

J

tn

= 1 fJJC c" ’ ) ' ( x • У • z , t . —1 ) dG n -, + J JJJ c " ^FdG .

²'                                                t „ — V G n — 1

G n

^Tn — 1

n —1

Предположим, что уравнению (14) с одними и теми же условиями (16)-(20) удовлетворяют два различных решения задачи c1 = c1 (x, y, z, t), c2 = c2 (x, y, z, t) . Для их разности c = c1 — c2 справедлива следующая начально-краевая задача:

дc  д(uc)  д(vc)  д((w+wg)c)     'д2c  д2c1  д'д

+++= Ц h I++Ц дt дx ду         дz          V8x 2  ду J  8z V c ( x, y, z, 0 ) = 0, ( x, y, z ) e Gn—1,

— на гранях S 1, n —1 , S 2, n —1

— на поверхности S ₆ , _n _₁

V V V

• 3,    n —1 ,      4, n —1 ,      5, n —1

*      *

c = c — c = 0 ;

8 c

8 z

w

— w g - ( c 1 — c 2 ) =

H v

w g

. H v

Для функции c равенство (33) примет вид с учетом равенств (34)-(36)

• ¹    JJJ c ² ( ^x , y , z , t n ) ^dG n —1

• ²    G n — 1

tn

+       H h|Ic 1 +H h v xx j

G n

д c

• 3    t n    rr

+ — J JJ w c^г dxdy dt +

• ²    t n — 1 V S 6,1                   J

dt = 0.

V S 6, n — 1

>²      7д~А2

1 д c ] + ц _v | I I V д z J

dG n —1

Поскольку wg > 0 и другие известные величины под знаком интегралов положительны цh>0, цv>0 то равенство (36) выполняется лишь при условии

c ( x , y ^,z, t ) = ⁰,    ( x , У , ^z )^e G n _ 1 , t „ _ 1 <  t <  t n ,                                     ⁽³⁸⁾

что и завершает доказательство единственности решения начально-краевой задачи (14)-(20).

В случае замены граничного условия (20) на соотношение (21) получаем вместо выражения (37) равенство вида tn

2 JJJ c ^{2 ( x} ’ У , ^z ’ t n ) ^dG n —1 ⁺ J JJ

^G n — 1                                           t n — 1 V ^S 6, n — 1

f           ' д c 1

+ J   Hh ItI +H h\ Л t,l         V8x J      V8у

tn

G n

V S 6, n — 1

w

2 ^g

—

ац _v I c² dxdy dt +

или

8 c

>²      7д~А2

I д c 1

I +H v I I V д z J

dG n —1

dt = 0.

Потребуем выполнения неравенства

2 w g ^—a H v ^ ⁰,    ( x , У , ^z )^{e S} 6, n —1 ,   t n —1 <  t <  t n

w g

2 ц v ’

( x , У , ^z )^e S 6, „ —1 ,    t n —1 <  t <  t n ,

Механика

тогда все слагаемые в равенстве (39) неотрицательны и равенство нулю возможно тогда и только тогда, когда c ( x , y , z, t ) = 0,    ( x , y , z ) e G_n _₁, t_n _₁ <  t <  t_n , что и означает единственность решения и в этом случае.

Рассуждения аналогичным образом повторяются для всех слоев временной сетки ωτ. Изменение граничных условий, связанное с непрерывным изменением рельефа дна в зависимости от временной переменной требует дополнительного исследования и выходит за рамки данной статьи.

Теорема. Пусть дана система уравнений

5 c ( ⁿ )    s ( uc ^{( n} ) ) s ( ^{vc ( n} ) ) a ( ( w + w g ) c ^{( n} ) )       _v2 c ( ⁿ ) d ² c ( ⁿ П    d a d c ( ⁿ )

+ F ,

+++= Ц h              ++Ц v d t      dx        dy            dz            ^ dx2    dy2 J  dz ^    dz

< ( x , y , z ) e G n -I , G n -I = { 0 <  x <  L x , 0 <  y <  L y , 0 <  z <  H^{n - 1} ( x , y , t n _ ) } ,

H ^{( n} ) = h ^{( n} -1 ) _ ^£ w N J c ^{( n} ) dt ,   n = 1,2,

^P     n =1 t i

N

в односвязной области Qn_1 = Gn_1 x(tn 1 < t < tn),  Gn 1 =(0 < x < Lx ,0 < y < Ly ,0 < z < H(n1)( x, y, tn _1)),    с до статочно гладкой границей, определяемой гладкостью функции z = H(n1)(x, y), 0 < x < Lx, 0 < y < Ly с начальными и граничными условиями (16)-(20). Пусть функции решения c(n)(x, y, z,tn 1) , вектора скорости водной среды ||u, v, w + wg|| , начального условия c(n-1) (x, y, z, tn_1), правой части F (x, y, z, t), граничного условия c* (x, y, z, t), коэффициента вертикального турбулентного обмена цv = цv (z), (x, y, z)e Gn_ 1 удовлетворяют следующим условиям гладкости:     c(n)(x,y,z,tn_1 )e C2 (Qn_1 )nC(Qn_1),         gradc(n*e C(Qn_1),

|| u , v, w + wg||r e C1 (Q n _1 )n C (Q n _1 ) ,             c(n-1)( x, y, z, tn _1 )e C ( Gn _1 ) ,              F ( x, y, z, t )e C (Q n _1 )      , ц v ( x, y, z )e C1 ( Gn _1 )n C ( Gn _1 )         ,          c *( x, y, z, t )e C ( Sn _1 )x[ tn _1 < t < tn ],         Sn _1 = Gn _1\Gn _1         ,

5 c *

— e C ((0 < x < Lx, 0 < y < Ly, z = H-n_1) (x, y))x[ tn _1 < t < tn ]), а также условиям согласованности граничных и начальных условий c*(x,y,z,0) = c0(x,y,z),

( x , y , z ) e S n _1 \ ( 0 <  x <  L x ,0 <  y <  L y , z = H ^{( n} 1 ) ( x , y ) ) ,

-c0- = _-цлc*,    (0 < x < Lx,0 < y < L , z = H(n 1) (x,y)),   тогда решение данной задачи существует и един- dz     wg        v                   y ственно.

Замечание. В случае замены граничного условия (20) на граничное условие (21), в качестве достаточного условия выполнения предыдущей теоремы следует добавить неравенство (40).

Исследование непрерывной зависимости решений начально-краевой задачи транспорта взвеси от начальных, граничных условий и функции правой части . Следующий этап связан с исследованием непрерывной зависимости решения от функций правой части, граничных и начальных условий для системы (14)– (15).

Будем предполагать, что

**

c >  c ₀ ^ const >  0,

⁰ <  ^x <  ^L x , ⁰ <  у <  ^L y , ⁰ <  ^z <  ^{H (} n ) ( ^x , у , t n _ 1 ) , t n _ 1 <  t <  t n .

Введем для удобства обозначения: объединение всех частей боковой цилиндрической поверхности

(границы области G_n-1 ) обозначим как S_c , _n _1 , а нижнее основание области G_n _1 _   S b , _n _1 . В силу условий глад-

кости, перечисленных в условиях вышеупомянутой теоремы, достигаются экстремумы функций на ограничен-

ных замкнутых множествах:

M

3, n _1

M 1, -1 ■ mmax !l c " 'В • M 2, - -* max |

^ max ^{ц _h ^} , M 4, n _1 ■ max    { u , v

S c , n _ 1                                          S c , n _ 1 ^x[ t n _ 1 < t < t n ^]

dc(n)    dc(n) > dx ’ dy    >

} , M 5, n _1 ■ min

G n _ 1

{ ц h , ц v } .

Будем ориентироваться на уравнение (31), если используется граничное условие (20), и равенство (32) — в случае граничного условия (21). Привлекая неравенство Фридрихса, имеем цепочку неравенств:

д c ⁽ n )

Ш ^д c

Ц h        +Ц h г        дx

G n

⁷n - 1

и

+ M_z

д c ⁽ n )

д y

+ Ц v

2 д c ⁽ ))

V д z

dG n -1 ^

> min

G n - 1

dG n -1 >

> M 5, n -1

r n2

V

⁷n - 1

V

r

11    1

Lx² L y ²   ( H ( n -1 ) ) ²

JJJ( c " ) ) 2 dGn -

G n - 1

Обратимся к уравнению (26), из которого в силу (42) и (43) получим неравенство:

JJJ( c'" ) ) ^{2 dG}- -+ ^{2 M} 5

G n - 1

5, n -1

r n2

r

11   1

^L x ²

L y ²    ( H ⁽ n ^{- 1 )} ) ²

n

^{+ 3} J JJ w g ( c ⁽ n ) ) ^dxdy ^dl < JJJ

t n - 1

V Sb, n - 1

чГ.

G n - 1

c 0 ^{2 dG} n -1 ⁺ M,

4, n -1

t n

tn

J JJJ( c- n ) ) dG n -1 dl +

' n - 1 V ^G n - 1

n

J JJ(c *) dSn-1dl+

+ 2 M 2, n -1 M з, n -1

t n - 1 t n r

V ^s« - 1

J JJ c * dS n - 1 d + 2 M- J JJJi FvG ,

n -1

) dl .

t n - 1

S c

t n - 1

V g . - 1

Из неравенства (44) следуют два неравенства

JJJ( c " ) ) 2 dG - -

G n - 1

+ 2 M, „_, M -,

< JJJ c 0 ² dG n -1 + M 4, n -1

G n - 1 n Г .

t n

JJJ( c ⁽ n ) ) 2 dG n

G n - 1

n 2

J JJ ( c ) dS n - dl + 2 M 2, n -1 M 3

t n - 1

V ^S c , n - 1

где ^M 6, n -1

2 M

5, n -1

r n2

r

11   1

' n

J JJ( c *) dSn-1dl+

t n - 1

. Sc , n - 1 t n r

J JJ c -| dS , - 1 d + ² M , J JJJ| F\dG ,

n -1

) dl .

t n -1

n

Sc

t n - 1

V G n - 1

6, n -1

r„.

JJJ c 0^{2 dG} n -1 ⁺

V G n - 1

tn (

J JJ c -| dS n - dl + 2 M 1, n -j JJJ| F l dG n

n -1

t n - 1

. Sc , n -

-1

' n - 1 V ^G n - 1

л Л (46) dl .

7  7

Lx ²    Ly ²    ( H ( n -1 ) ) ²

.

Из полученных неравенств следует непрерывная зависимость (устойчивость) решения задачи (14)-(20) от функций: начального условия, граничных условий и правой части, в норме L 2 для любого момента времени 0 <  T < +» , а также в интегральной по времени норме L ₂.

Очевидно, что при выполнении неравенства (45) и условий теоремы начально-краевая задача (14)-(19), (20) также будет иметь решение, непрерывным образом зависящее от функций: начального условия, граничных условий и правой части в соответствующих нормах.

Обсуждение и заключения. Новизна предложенной нестационарной пространственно-трехмерной математической модели транспорта взвесей состоит в том, что наряду с учетом процессов адвективного переноса, микротурбулентной диффузии и гравитационного осаждения частиц взвеси модель описывает изменение геометрии дна, вызванное осаждением частиц взвеси или подъемом частиц донных отложений. Выполнена линеаризация соответствующей начально-краевой задачи на временной сетке и получены для произвольного временного шага l_n _1 <  l <  l_n условия единственности решения начально-краевой задачи и непрерывной зависимости от входных данных — от функций начального условия, граничных условий и правой части в норме гильбертова пространства L 2 в интегральной по времени норме L 2 для двух вариантов граничных условий.

Механика