Построение и исследование структуры сложной сети YouTube - каналов

В последние годы сложно-сетевой подход, использующий понятия и методы математики, физики, информатики и социологии, сформировался в универсальный инструмент исследования реальных сложных систем, моделируемых как сложные сети [1].

Возникшая в начале XXI века наука о сложных сетях позволяет описывать существующие в природе и обществе сети, обладающие нетривиальными топологическими свойствами, которые не являются типичными для случайных графов или регулярных решеток. Как правило, такая сеть содержит малое число узлов большой степени – хабов (от английского hub – ядро, концентратор), существенно определяющих её свойства и возможности функционирования. При этом оказалось, что большинство реальных сетей (биологических, технических, социальных) являются сложными [2].

Наглядным примером сложной и социально значимой системы является видеохостинг YouTube . Сервис содержит около 2 миллиардов каналов и обеспечивает возможность подписываться на понравившиеся каналы, проводить онлайн-трансляции; загружать, оценивать и комментировать видеоролики, а также делиться ими.

На протяжении всего своего существования YouTube достаточно сильно эволюционировал. Покупка компанией Google , блокировка и локализация в различных странах мира, коммерциализация, внедрение системы защиты авторского права – все эти этапы развития видеохостинга отразились в эволюции структуры YouTube как сложной системы [3].

По мере возрастания популярности YouTube , возрастал и интерес к изучению его структуры. Так, Джон Паолильо с соавторами исследовали историю контента YouTube как меняющуюся со временем сеть отношений между каналами, выраженную в плейлистах «Нравится/избранное». В своей работе они обсуждают, как внешние и внутренние факторы могут изменять тип контента во всей сети и отдельно выделенных кластерах [4]. Малек Джебабли с соавторами проводили сравнительный анализ сети YouTube на уровне пользователей (каналов) и групп (сообществ пользователей) и показали, что два разных типа рассматриваемых сетей имеют схожую структуру [5]. Результаты этого исследования позволяют лучше понять отношения между мезоскопическими и макроскопическими свойствами онлайновых социальных сетей как с топологической, так и с функциональной точки зрения.

Тем не менее, несмотря на популярность видеохостинга YouTube , он до сих пор остаётся малоизученным. И это при том, что его социальная значимость, как совершенного ресурса обмена информацией разного рода, постоянно возрастает. Функционирование видеохостинга привлекает внимание обыкновенных пользователей и организаций. Интригующей остаётся роль YouTube как информационного оружия в избирательных компаниях, брекзите, формировании общественного мнения или фейков, и многом другом. Все вышеперечисленные процессы на уровне каналов протекают с учетом структуры сети подписок, но под управлением системы рекомендаций, принцип работы которой досконально не известен. Чтобы изучать, понимать и управлять процессами в сети YouTube , особенно с учетом этой неопределенности, необходимо как можно более адекватно представлять структуру базовой сети и закономерности ее эволюции. Попытка такого исследования предпринята рамках данной работы.

Метод исследования

YouTube сформировал гигантскую сеть, – изучение ее возможно только на уровне подсетей (выборок). Полная карта YouTube доступна только Google / YouTube , а данные для отдельных видео доступны

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №1, 2022 год только через функции поиска и просмотра и не могут быть отобраны действительно случайным образом (например, вследствие спонсируемых функций поиска и алгоритмов рекомендаций по видео) [6]. Поэтому в данной работе анализировалась структура сети YouTube на уровне каналов: узлам соответствовали YouTube -каналы, а направленные связи - отношениям подписки.

Для проведения исследования необходимо было построить выборки с использованием просмотра и сканирования API общедоступных данных Google / YouTube с последующем извлечением сетевых данных. Для каждой из сетевых карт вычислялись основные сетевые характеристики и определялась структура сообществ, из анализа временной последовательности сетевых карт извлекалась информация о закономерностях эволюции сети каналов YouTube.

Построение выборок

Данные о сети каналов YouTube (ее подсети) можно получить из репозитория, специализирующегося на анализе сложных сетей, например, Network Data Repository [7]. Однако, такие данные, во-первых, достаточно устаревшие, и во-вторых, позволяют исследовать только статический граф (вершины и направленные ребра), не давая возможности получить информацию о динамике изменений сети (правилах эволюции), а также природе сообществ. Поэтому для построения выборок был использован сканер сетевых данных, позволяющий собрать актуальную и более полную информацию о YouTube -каналах и их подписчиках.

Эмпирические данные собирались с помощью веб-приложения YouTube Data Tools . Этот инструмент позволяет сканировать данные платформы YouTube через YouTube API v 3 и формировать протокол в стандартных форматах файлов для дальнейшего анализа в других программных пакетах [8].

При сборе данных сканирование начиналось с 50 самых популярных YouTube -каналов, то есть таких, которые имеют наибольшее число подписчиков. Для изучения закономерностей эволюции сети сканирование при глубине сканирования, равной «2», проводилось 5 раз с временным промежутком в 2 недели с 15 марта по 15 мая 2021 года. Дополнительно для изучения вопроса о зависимости структуры подсети от глубины сканирования аналогичная сеть была собрана с помощью глубины «3» в августе 2021 года. Наконец, для исследования зависимости структуры подсети от локализации в мае 2021 года были аналогичным образом собраны данные по русскоязычным каналам.

Глубина сканирования показывает насколько «глубоко» должен работать сканнер (см. рис. 1).

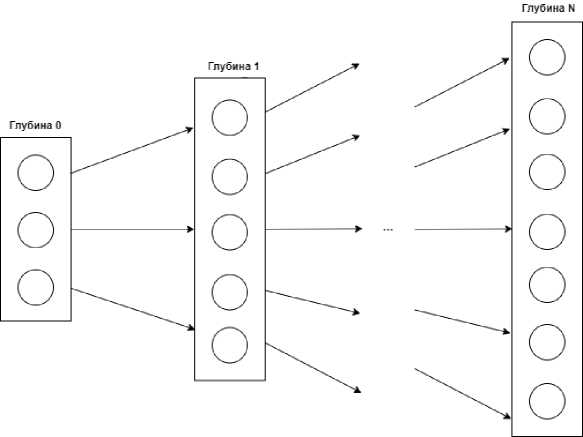
Рис. 1. Схема работы сборщика данных

Стартуя от начального узла при каждом значении глубины сканер добавляет полученную информацию о каналах, на которые текущий узел подписан, в текстовый gdf-файл. Данный файл содержит описание сети, каждая строка списка представляет ребро, задаваемое уникальным идентификатором входного и выходного канала, а также логическим значением, указывающим, является ребро направленным или нет (см. рис. 2) [8].

16104 edgedef>nodel VARCHAR,node! VARCHAR,directed BOOLEAN

16105 UCpEhnqL0y41EpW2TvWAHD7Q, UC6uPyCHIzAx4pb4Pd0d.j_mw, true

16106 UCpEhnqL0y41EpW2TvWMD7Q, UCA14 6BZ s Jj XCmOYcfbM-kqQ, true

16107 UCpEhnqL0y41EpW2TvWMD7Q, UCHu48NlukyWGqjh3DUKcBmA, true

16108 UCpEhnqL0y41EpW2TvWAHD7Q,UCcIPw0eP8KQPUXh5rK4wp3A,true

16109 UCpEhnqL0y41EpW2TvWAHD7Q,UCOQNJjhXwvAScuELTTi7cQ, true

16110 UCpEhnqL0y41EpW2TvWAHD7Q,UCnpaBg-u_kHwzuPyaMcyJOw,true

16111 UCpEhnqLOy41EpW2TvWAHD7 Q,UCQmxcMxjYcBM5Ре14qUW2hA,true

16112 UCpEhnqLOy4!EpW2TvWAHD7Q,UCkRfArvrzheW2E7b6SVT7vQ,true

16113 UCpEhnqL0y41EpW2TvWMD7Q, UCw7x jxzbMwgBSmbeYwqYRMg, true

16114 UCpEhnqLOy41EpW2TvWAHD7Q,UCF_cPp4EXD_BFUkL8HHJ8BA,true

16115 UCpEhnqL0y41EpW2TvWAHD7Q,UCtahuT3COFyZ8xs4TDAfIjw,true

16116 UCpEhnqL0y41EpW2TvWAHD7Q,UCBIT1FSJW6yTlzqK-3iFDWg,true

16117 UCpEhnqL0y41EpW2TvWAHD7Q,UCBz9qbqujcjIavFmBJW2oZw,true

16118 UCpEhnqL0y41EpW2TvWAHD7Q,UC25he-g2TMwFx2AnEiCkrzA,true

Рис. 2. Структура данных, собираемая сканером, соответствующая списку рёбер

Построение сети и последующий ее анализ проводились с помощью библиотек tuber (удобный клиент для работы с YouTube API ) и igraph (инструментарий для анализа сложных сетей) языка статистического программирования R в среде разработки RStudio .

Анализ структуры сложной сети YouTube – каналов

Общие характеристики

После построения сетей YouTube -каналов вычислялись общие характеристики (количество вершин и ребер), средние степени, значение коэффициента кластеризации, метрические характеристики, распределение степеней. Они представлены в таблице 1. Все сети являются связными.

Таблица 1. Основные характеристики построенных сетей. Сети 1-5 собраны при глубине сканирования «2», сеть 6 – при глубине «3». Сеть 7 получена сканированием русскоязычных каналов

	Сеть 1	Сеть 2	Сеть 3	Сеть 4	Сеть 5	Сеть 6	Сеть 7
Количество узлов	15949	15997	15976	16037	16095	402093	10383
Количество ребер	305703	306533	303974	305468	306477	8670620	142198
Направленная сеть	Да	Да	Да	Да	Да	Да	Да
Диаметр	14	14	14	14	14	15	15
Радиус	2	2	2	2	2	6	2
Среднее расстояние	4.26	4.26	4.26	4.26	4.26	5.08	4.84
Коэффициент кластеризации	0.067	0.067	0.066	0.065	0.066	0.014	0.102
Коэффициент кластеризации случайной сети того же размера	0.0024	0.0024	0.0024	0.0024	0.0024	0.0001	0.003
Средняя степень	38.3	38.3	38.1	38.1	38.1	43.1	27.4
Средняя полустепень ис-хода/захода	19.2	19.2	19	19.1	19	21.6	13.7

Для сетей 1-5, полученных при глубине сканирования «2», и по сути описывающих эволюцию практически одной и той же подсети каналов YouTube, основные характеристики, как и можно было ожидать, очень близки по значениям. Можно видеть, что сеть растет даже за такой небольшой промежуток времени. Неожиданно, что третья карта является наименьшей по количеству вершин и рёбер среди других карт. Возможно, причиной такого явления является то, что на момент сбора карты третьей сети происходили различные блокировки доступа к платформе YouTube. Ожидаемо, за всё время исследования в сети не изменялись диаметр и радиус. Это, по всей видимости, следствие заданной глубины сканирования «2», хотя инициация просмотра от 50 наиболее популярных каналов могла привести и к большим значениям радиуса сети. Незначительно менялась средняя длина пути.

Значения коэффициента кластеризации, отражающего вероятность того, что соседи узла связаны между собой (плотность треугольников), на первый взгляд, не велики - 0.065 - 0.067, но сравнение со значениями коэффициентов кластеризации для случайных сетей Эрдеша-Реньи с тем же количеством вершин и ребер (или при рандомизации исходного графа), дает 0.0024 (почти в 30 раз меньше). Таким образом, исследуемая сеть является высоко кластеризованной, что вместе с небольшими значениями среднего расстояния между узлами указывает на ее мало-мировой характер [9].

Сеть 6, полученная при глубине сканирования «3», имеет более высокие значения базовых характеристик, чем у предыдущих сетей. Значение коэффициента кластеризации - 0.014 - существенно отличается от значения коэффициента кластеризации для случайной сети Эрдеша-Реньи с тем же количеством вершин и ребер, равного 0.0001 (в 140 раз меньше). При увеличении числа вершин по сравнению с сетями 1-5 в ~25 раз среднее расстояние между вершинами этой карты сети увеличилось менее чем на 20%, что опять-таки подтверждает мало-мировое свойство.

Базовые характеристики вычислялись также для сети 7, полученной из сканирования русскоязычных каналов. Несмотря на то, что это совсем другая подсеть сети каналов YouTube , свойства ее очень близки к сетям, рассмотренным выше.

Таким образом, можно утверждать, что сеть каналов YouTube в целом, является значительно кластеризованной и мало-мировой.

Распределение степеней

Одной из важнейших характеристик структуры сложной сети является распределение степеней. Поскольку изучаемые сети ориентированные, были построены распределения полных степеней, полустепеней захода и полустепеней исхода. На рисунках 3-5 представлены распределения для сети, полученной с при глубине сканирования «3».

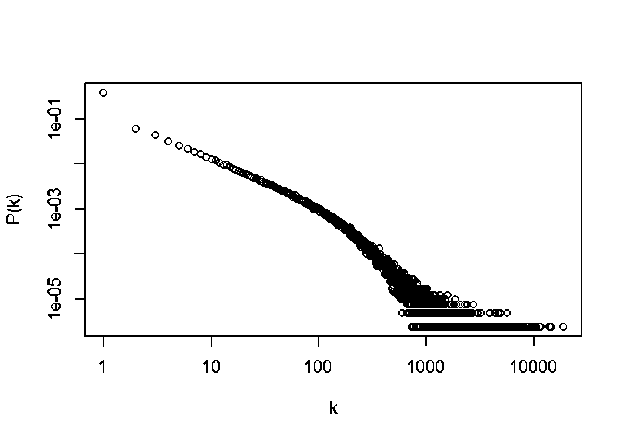
Рис. 3. Распределение степеней сети 6 в log-log масштабе

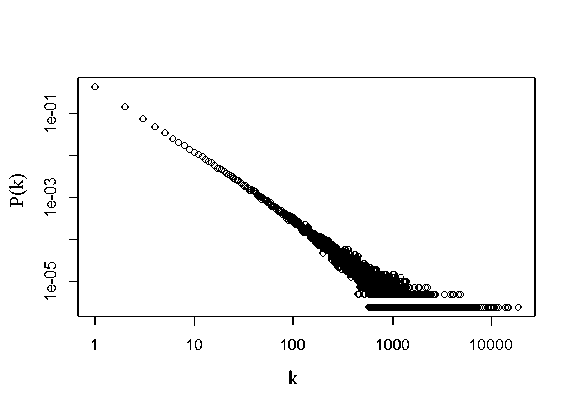
Рис. 4. Распределение полустепеней захода сети 6 в log-log масштабе

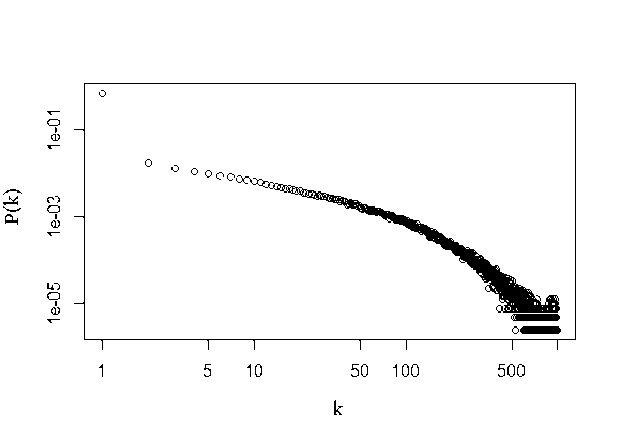
Рис. 5. Распределение полустепеней исхода сети 6 в log-log масштабе

Форма распределений в log - log масштабе с прямолинейным участком указывает на то, что исследуемая сеть является безмасштабной, с распределением степеней, описываемым степенной функций P(k)~k-^Y [9]. При малых степенях есть отклонения от прямой, это может быть связано с малой глубиной сканирования во время сбора данных. Значение показателя степени у были получены с помощью метода максимального правдоподобия (1):

y^nte^n^]"1,  (1)

KminJ где у - оценка показателя степени, и - число узлов в сети, kmin - минимальная степень, ki - степень I-го узла [10]. Значения xmin при аппроксимации выбирались так, чтобы описать прямолинейную часть распределения и толстый хвост. Результаты приведены в таблице 2.

Таблица 2. Оценки показателя степени для распределений степеней сетей 1 – 7

Режим	Значения	Сеть 1	Сеть 2	Сеть 3	Сеть 4	Сеть 5	Сеть 6	Сеть 7
	k min	32	33	32	32	32	53	24
Полная		2.01 ±	2.01 ±	2.003 ±	2.002 ±	2.003 ±	2.007±	2.01 ±
степень	у	0.02	0.02	0.02	0.02	0.02	0.004	0.02

Режим	Значения	Сеть 1	Сеть 2	Сеть 3	Сеть 4	Сеть 5	Сеть 6	Сеть 7
Полусте-	к т1п	15	15	15	15	15	188	9
пень за-	у	2.01 ±	2.01 ±	2.01 ±	2.01 ±	2.01 ±	2.001±	2.01 ±
хода		0.02	0.02	0.02	0.02	0.02	0.014	0.02
Полусте-	ктт	41	41	41	41	41	39	29
пень ис-	у	2.01 ±	2.01 ±	2.01 ±	2.01 ±	2.01 ±	2.005 ±	2.02 ±
хода		0.02	0.02	0.02	0.02	0.02	0.004	0.03

Таким образом, распределения степеней всех анализируемых сетей описываются степенным законом Р(к')~к-^Г с показателем степени у ~ 2. Такой характер распределения указывает на то, что сеть является растущей с предпочтительным присоединением (то есть новые поступающие в сеть вершины соединяются с уже присутствующей в сети вершиной с вероятностью П(к) тем большей, чем больше ее степень). В базовой модели безмасштабных сетей - модели Барабаши-Альберт - П(к)~к, и это приводит к сетям с распределением степеней с у = 3. Полученное для сетей YouTube значение у « 2 указывает на присутствие дополнительных механизмов эволюции сети: удаление узлов, создание новых связей между «старыми» узлами, старение узлов и, наконец, нелинейное предпочтительное присоединение [9].

Изучение характера предпочтительного присоединения

Для исследования характера предпочтительного присоединения использовалась следующая методика. Рассмотрим сеть, для которой у нас есть две разные карты: первая, взятая в момент времени t, а вторая в момент времени t + At (см. рис. 6 a ). Для узлов, которые изменили свою степень в течение At, измеряем изменение степени Дк ; . Согласно предпочтительному присоединению, относительное изменение Aki/At должно быть пропорционально вероятности Ak;/At ~П(к ; ), обеспечивая функциональную форму предпочтительного присоединения. На практике полученная кривая Aki/At может быть зашумленной. Чтобы уменьшить этот шум, измеряют кумулятивную функцию предпочтительного присоединения (2):

я(к) = Е^;=оП(к;). (2)

При отсутствии предпочтительного присоединения имеем П(к ; ) = const, следовательно, кумулятивная функция я(к)~к. Если имеет место линейное предпочтительное присоединение, то есть если П(к ; )~к, ожидается, что кумулятивная функция п(к)~к² (см. рис. 6 b ) [9].

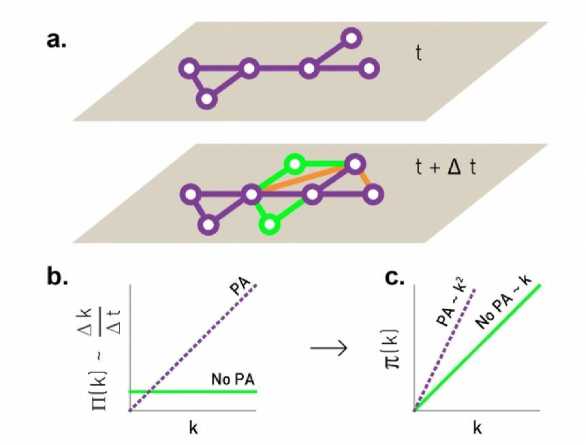
Рис. 6. Измерение характера предпочтительного присоединения

Для оценки показателя предпочтительного присоединения использовались пять карт, на основе которых вычислялась кумулятивная зависимость частоты изменения степени вершин, которая представлена на рисунке 7. Синие точки соответствует полученной зависимости, а оранжевая прямая линия соответствует зависимости в случае линейного предпочтительного присоединения. Сравнение двух зависимостей указывает на присутствие нелинейного предпочтительного присоединения в исследуемой сети с показателем нелинейности меньше 1, а именно 0.7. Стоит отметить, что нелинейность также указывает на дополнительные механизмы, влияющие на эволюцию сети [9].

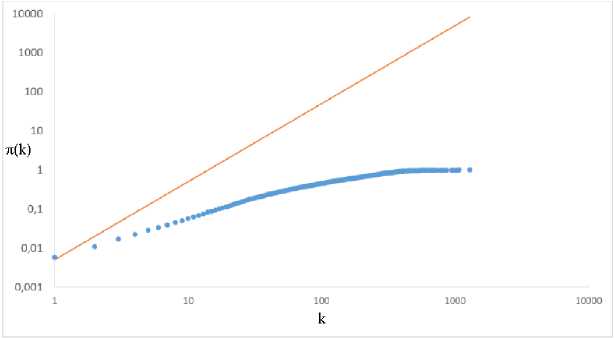
Рис. 7. Зависимость п(к), вычисленная для фрагмента сети каналов YouTube. Синие точки соответствуют эмпирической зависимости, прямая линия – оценочная – соответствует значению показателя предпочтительного присоединения а = 1

Были сгенерированы растущие сети с нелинейным предпочтительным присоединением Т7(к ( )~к^0,7. На рисунке 8 показано распределение степеней, значение показателя у составило у = 2.010 ± 0.007. Сходство топологий эмпирической и сгенерированных сетей позволяет рассматривать нелинейное предпочтительное присоединение как ключевой механизм эволюции сети, позволяющий генерировать сети, статистически схожие с исследуемой сетью и изучать на них процессы распространения информации.

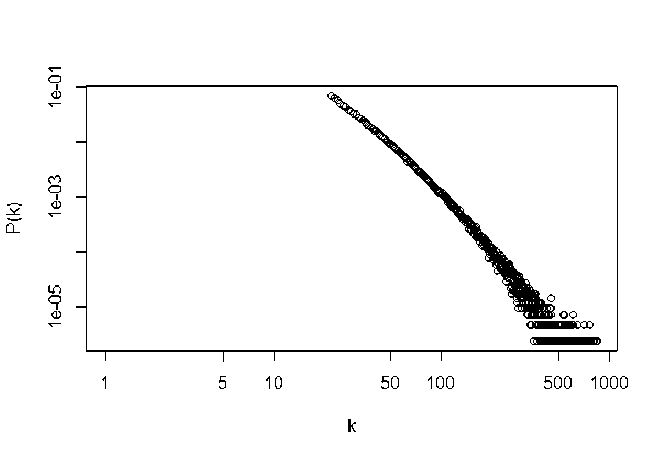
Рис. 8. Распределение степеней сгенерированной сети, у = 2.010 ± 0.007

Корреляции степеней

Для определения наличия и характера корреляций степеней вершин вычислялся коэффициент ассортативности, отражающий тенденцию узлов сети соединяться с другими узлами, близкими по степени. Для сетей, собранных при глубине сканирования «2», коэффициент ассортативности равен — 0.058, для сети, полученной при глубине «3», равен — 0.096. Для более детального анализа корреляций также строилась зависимость средней степени ближайших соседей вершины от её степени (k_nn)(k). На рисунках 9-10 приведены графики (k-^Xk) для сетей, полученные при глубине «2».

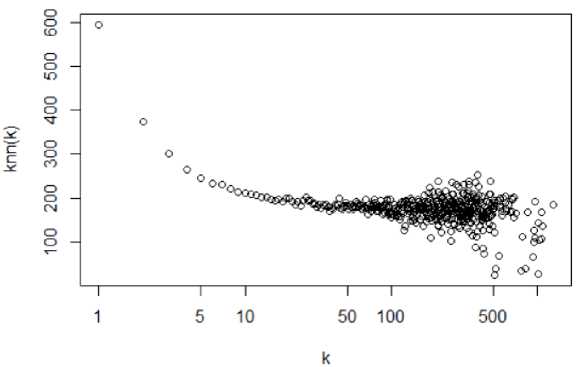
Рис. 9. Зависимость средней степени ближайших соседей вершины от её степени (k_nn)(k) для сети

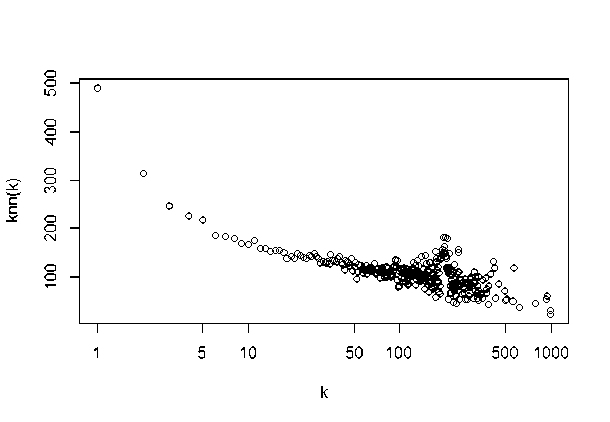
Рис. 10. Зависимость средней степени ближайших соседей вершины от её степени (k_nn)(k) для сети 7 (русскоязычная подсеть)

Отрицательное значение коэффициента ассортативности и убывающий характер зависимостей указывают на то, что сети слабо-дисассортативны, то есть вершины с большой степенью имеют тенденцию соединяться с вершинами малой степени и наоборот. Однако известно, что сети с ярко выраженной структурой сообществ, что можно ожидать для сети каналов YouTube , как правило, ассортативны. Наблюдаемая дисассортативность может быть вызвана конфликтом между корреляциями степеней и масштабно-инвариантным характером распределения степеней (как следствие того, что сеть рассматривается как простая, т.е. без кратных связей между узлами) [9].

Для подробного изучения характера корреляций степеней вершин детальнее анализировалась сеть, полученная при глубине сканирования «3», график зависимости (knn)(k) которой имеет аномаль- ную форму. Есть растущая часть графика при небольших значения к, указывающая на ассортативность, и убывающая часть графика при больших к, свидетельствующая о дисассортативном характере (см. рис. 11).

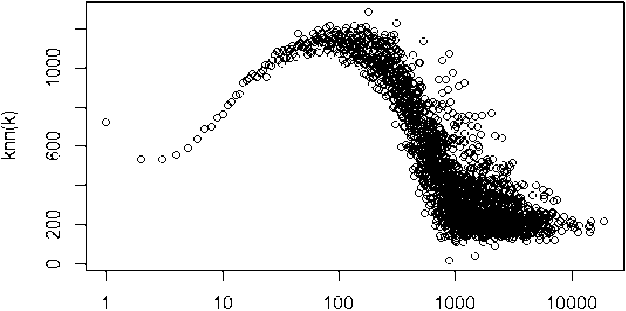
Рис. 11. Зависимость средней степени ближайших соседей вершины от её степени (к_п?г)(к) для сети 6

В сети с корреляциями степеней е_кк, ожидаемое количество связей между узлами со степенями к и к' равно Е_кк, = еккАк^, где (к) - средняя степень сети, а N - число узлов в сети. Возьмем два крупнейших узла сети, они имеют степени к = 18917 и к' = 14762. В предположении нейтральной сети и с учетом значений (к) и N для сети 6 (см. рис. 3) имеем (3):

Екк' =

кр_ккгр_к1 М

18917*14762

43.1*402093

16 . (3)

Таким образом, учитывая размер этих двух хабов, они должны быть соединены друг с другом примерно 16 связями, чтобы соответствовать нейтральной природе сети. Тем не менее, в простой сети мы можем иметь только одну связь между ними, что и вызывает конфликт между корреляциями степеней и масштабно-инвариантным свойством. Тот факт, что не разрешены кратные связи (представление простой сети), делает сеть дисассортативной - явление, называемое структурной дисассортативно-стью. Для малых к и к’ ожидаемое количество связей Екк‘ также мало, то есть ожидается, что между двумя узлами будет меньше одной связи. Мультисвязи ожидаются только для узлов, степень которых превышает некоторый порог к₅ . Можно оценить к₅ , называемое структурным отсечением, для изучаемой сети (4):

к = ((k)N)2 « 4124, (4)

Чтобы понять последствия структурного отсечения, нужно определить, есть ли в сети узлы, степень которых превышает к₅. Для этого мы сравниваем структурное отсечение к₅ с естественным ограничением на наибольшую степень в сети заданного размера со степенным распределением степеней (5):

ктах-N^1 « 397240.

Из сопоставления к₅ и к_тах , можно сделать вывод о присутствии в сети структурной дисассорта-тивности. Иными словами, узлы, чья степень находится между к₅ и к_тах , могут нарушать Екк ' > 1, то есть сеть имеет меньше связей между узлами, чем предсказано. Поэтому такие сети проявляются как дисассортативные.

Для определения, являются ли корреляции, наблюдаемые в сети, следствием структурной дисас-сортативности или они генерируются каким-то неизвестным процессом, который приводит к корреляциям степеней, использовалась сохраняющая степень рандомизация. Если в результате зависимости (к_пп')(к') реальной и рандомизированной сетей неразличимы, то все корреляции, наблюдаемые в реальной системе, являются структурными и полностью объясняются распределением степеней. Иначе, если зависимость (к_пп)(к) рандомизированной сети не показывает корреляции степеней, в то время как для реальной сети показывает, то существует некоторый неизвестный процесс, который генерирует наблюдаемые корреляции степени [9]. Сравнение (к_пп)(к) для сети 6 и соответствующей рандомизированной сети показано на рисунке 12.

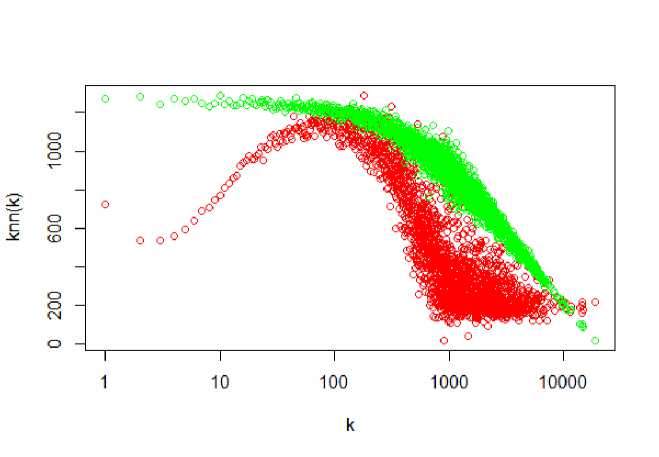
Рис. 12. Зависимость средней степени ближайших соседей вершины от её степени (к_пп)(к) . Красная зависимость соответствует эмпирической сети 6, а зелёная – рандомизированной сети

Ассортативность в левой части, при небольших значениях к разрушилась, т.е. она присуща сети, что и является типичным для сетей со структурой сообществ, а дисассортативность при больших к, очевидно, является структурной.

Определение структуры сообществ и их интерпретация

Еще одной структурной особенностью, существенно влияющей на процессы в сети, являются сообщества. Для выделения сообществ использовался набор алгоритмов, реализованных в библиотеке igraph .

При изучении сообществ в сетях необходима метрика, чтобы объективно оценить, насколько «хорошим» является конкретное разделение сети на сообщества. Одной из таких метрик является мера модульности, указывающая насколько отличается локальная плотность связей в подсетях, определенных этим разделением, от ожидаемой плотности в случайной сети. Более высокое значение модульности подразумевает лучшее разделение. Значение модульности, равное 0, соответствует случаю, когда вся сеть рассматривается как одно сообщество [9].

Для изучаемых сетей наилучшие значения модульности даёт алгоритм Louvain . Этот алгоритм хорошо работает для больших сетей, особенно с высоким коэффициентом кластеризации и распределением степеней с толстыми хвостами, как это имеет место в сети каналов YouTube . Он выполняет так называемую агломеративную иерархическую кластеризацию, в которой узел назначается кластеру, если это максимизирует модульность сети, и продолжает до тех пор, пока либо не останется ни одного не назначенного сообществам узла, либо модульность не может быть увеличена дальше. Кластеризация по модульности несовершенна: иногда она выявляет несуществующие связи между кластерами на основе слабых ложноположительных связей и имеет тенденцию давать большое количество кластеров в разреженных сетях [11]. Тем не менее, она хорошо работает для обнаружения четко определенных кластеров в больших сетях, как ожидалось в случае YouTube .

Для каждой сети фиксировалось количество полученных сообществ и значение модульности (см. табл. 3).

Таблица 3. Результаты анализа структуры сообществ в сети

	Глубина 2	Глубина 3	Русскоязычный сектор
Количество сообществ	12	62	13
Модульность	0.4	0.5	0.5

Для понимания природы сообществ были определены соответствующие им тематики. Для этого извлекались и анализировались жанры видеороликов для каждого из каналов из больших сообществ, найденных алгоритмом Louvain (см. рис. 13-15). Из диаграмм видно, что в исследуемых сетях главные жанры контента носят развлекательный характер, что подтверждает то, что YouTube по большей части был и остается развлекательной платформой. Также среди жанров русскоязычного сектора были обнаружены сообщества, которые сконцентрированы на кинематографе. Возможно, это издержки более слабого соблюдения авторских прав в этом секторе.

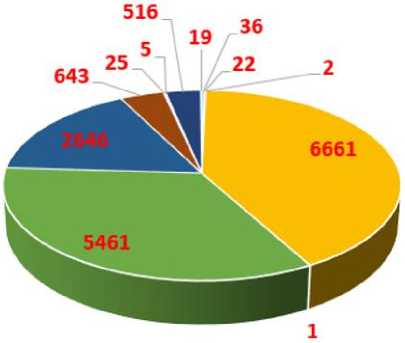
• ■    Игры, развлекательная программа

• ■    Игры, развлекательная программа

• ■    Видеоблог, развлекательная программа, DIY

• ■    Видеоблог, развлекательная программа, музыка

• ■    Развлекательная программа, музыка

Рис. 13. Жанры видеороликов в сообществах сети, полученной с помощью глубины «2»

• ■    Развлекательная программа, DIY

  
  
  

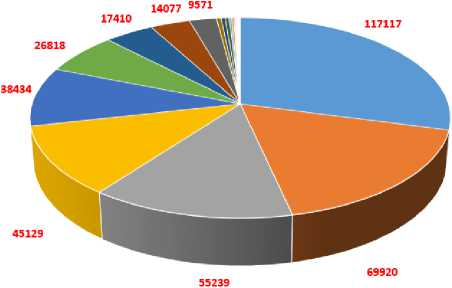
• ■    Развлекательная программа, Видеоигры

• □    Развлекательная программа, Видеоблог

Образование, музыка

• ■    DIY, музыка

• ■    Развлекательная программа, Музыка

• ■    Музыка, видеоблог

• ■    Развлекательная программа, Автомобили

• ■    Музыка, видеоблог

Рис. 14. Жанры видеороликов в сообществах сети, полученной с помощью глубины «3»

• ■    Кинематограф

  
  
  

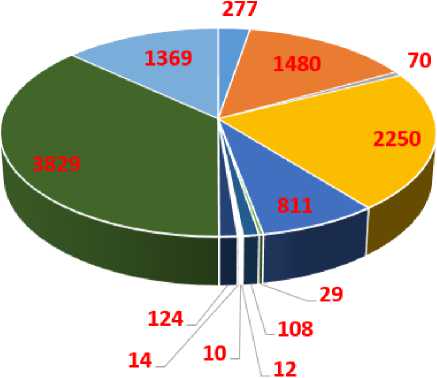
• ■    Видеоблог, развлекательная программа, DIY

Развлекательная программа

• ■    Музыка

• ■    Кинематограф

• •    Игры

• ■    Игры, развлекательная программа

Рис. 15. Жанры видеороликов в сообществах русскоязычного сектора

Заключение

Целью работы было изучение структурных особенностей сети каналов YouTube – распределения степеней, характера корреляций степеней вершин, а также структуры сообществ. Для проведения исследований были собраны различные карты подсетей исследуемой сети. Результаты анализа показывают, что построенная сложная сеть каналов YouTube является мало-мировой, масштабно-инвариантной с показателем, равным 2, относится к слабо-дисассортативным (причем дисассортативность носит структурный характер) и имеет хорошо выраженную структуру сообществ, коррелирующую с главными жанрами видеоконтента. Была изучена динамика роста степеней узлов, показано, что сеть является растущей с нелинейным предпочтительным присоединением с показателем, равным 0.7.

Полученные результаты позволяют генерировать сети, статистически подобные сети каналов YouTube , и исследовать в них особенности распространения информации [9].