Построение исключительных множеств для меры, разделяющие множества для меры

Уточнённый порядок играет важную роль в теории роста субгармонических функции, в ряде других разделов математики.

Абсолютно непрерывная функция /’C’. на полуоси ^^ называется уточнённым порядком, если выполняются следующие два условия :

• 1)    существует предел ■,

hm r }i\rp'{r '<- 0

• 2)                   .

В приложениях чаще всего используется не сам уточнённый порядок

^(■’. , а функ-ция

. Отметим следующее свойство уточнённого порядка.

Теорема 1. для любого ■ > 0 существует предел lira

= f

и этот предел равномерный на любом сегменте

Если ^C’. – уточнённый порядок, то существует дифференцируемый, и даже анали-тический, уточнённый порядок £ ( ■’. такой, что

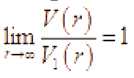
’I '

где            .

Поэтому предположение о дифференцируемости уточнённого порядка часто не ограничивает общности рассуждений. В дальнейшем мы будем предполагать, что функ-ция ^C’. является непрерывно дифференцируемой на полуоси .

Рост произвольной функции f(- . сравнивается с ростом функции вида

Множество функций вида множество степеней r , a

r'“ ^Inr) ' (ln;r) ‘...(Jn^J , где ^ где итерация логарифма. Например

– это более широкое множество, чем , или множество функций вида – вещественные числа, а I^я™ – это ж -тая In- r = In In r

Пусть – положительная функция на полуоси функции называется число

. Порядком

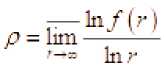
Важность понятия уточнённого порядка в теории роста функций можно усмотреть из следующей теоремы.

Положительная на полуоси функция называется регулярно меняющейся в смысле Караматы, если для любого существует конечный предел

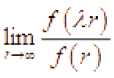
Пусть р ( t ) - некоторый уточнённый порядок. На пространстве R c определяется одно-параметрическое семейство преобразований Азарина A_t : R C ^R C , t e ( 0 ,~ ) , согласно формулам

^{р ( tE} )

P t A t P’Pt ^{( E} ) v ( t ) ^,

Для любого борелевского множества E .

Пусть ф e Ф ( R n ) . Формула переменных даёт

J ф ⁽ x ) dP t ⁽ x ) = 7П J Ф ( x ) ^dP ⁽ t ) • ^{( 1 )}

R П                         V ⁽ t ) R П t

В следующей лемме приводится оценка исключительного множества для меры

Лемма 5.1. Если точки x и y лежат в одной компоненте ^G i множества ^G η , то эти точки можно соединить цепочкой шаров вида C ( X s ,a s || x_s | ) , s = 1,2 ,...,m , где x s e E n ^G i .

Доказательство. Пусть H -^ множество точек, которые можно соединить цепочкой шаров указанного выше вида с фиксированной x ^e G i . Очевидно, что H - открытное.

Лемма 5.2. Пусть р ( r ) -б уточнённый порядок, р -^ положительная мера из класса M , ( р ( r ) ) и пусть G n - множество построено указанным выше. Тогда существуют система шаров C s'■= C ( x_s,a_s | X s | ) , где x s ^e G n , ^a s = ^a x_s , покрывающая множество ^G _n и величина M такая, что для любых r> 1 и n >  О выполняется неравенство

Е ( ^a s | ^x s | ) "  ¹ <  Mn^r n ¹

II x s II ^^r

Далее определим разделяющие множества для меры в пространстве R ² и изучим их свойства.

Пусть n = 2 , C s = C ( zs^,asrs ) -^ система кругов, имеющих кратность не выше числа ^θ 2 . Мы будем использовать следующие характеристики системы:

I L H ( r ) =    ^    a s r s <  Mnr.

C s nB ( 0 ,r ) * 0

Имеются место неравенства r s ( 1 - ^a s ) <^r,r s <2r . Тогда из леммы 5.2 следует, что

H ( r ) - S a_sr_s< 2 Mnr. ( 5.4 ) r_s≤ 2 r

2 ^L 0 ⁽ r ) =    £    arc sin ^a s <ⁿ   S ^a s <^ S    р^Л,

C s nK ( r ,2 r ) * 0                   ² C s nK ( r ,2 r ) * 0        ² C s nK ( r ,2 r ) * 0 V ( r s )

где K(r,2r)=B(0,2r)/C(0,r),S 1-^единичная окружность в пространстве R2. Величина 2 arc sin αs это угол, под которым круг Cs виден из начала координат Заметим, что rs (1-as)< 2 r,rs< 4 r,rs (1+ as)< 6 r, r„(1+aj>r,r >2r,rs(1—aj>1 r. s s        s3 s        s 3

Поэтому

0 ( r )

5 П 77      S ' ⁽ C s ) <^П^ 2 ^M 5 П

V ^{( r} ) C s nK ( r ,2 r ) * 0              ²

'((H'S;)

V ^{( r} )

≤πθMM η

22    5   6

где

M 5

r> 1 V ( r )        L      ' ([ 3 r '⁶ r । '^S 2 )

3 r 4 rv (t)^{,M 6}■ r>¹      V (r)

Из условия рe Mx(p(r)) и неравенства (2.3) следует, что M5<ж,м6<ж. Из полученного неравенства следует, что

0 ( r ) <П е 2 M 5 M 6 n = h ( п ) . ( 5.5 )

Пусть р —L положительная мера из класса M ^ ( p ( r ) ) , m —L произвольное натуральное число. Обозначим е 1 = £ 1 ( m ) = 2² — 1 , п = £ 2 , E n ^—L исключительное множество для меры р , описанное перед этим, M —L константа из леммы 5.2. Множество чисел ^R k строится таким образом R_k = ( 1 ^— Y k )( ^{1 + £} 1 ) k k ^e N ,где

Y k e [ 0 -Me 1 ] , причём γ k выбирается так, чтобы выполнялось соотношение { R k ^x S n - i } ⁿ { u ^C S } =0 . Из неравенства 5.4 следует, что такой выбор возможен.

Пусть теперь выбирается такое число m , для которого выполняется неравенство R k + i > R k ^{,k e} N .Это и есть ( 1 — Yk + 1 )( ^{1 + e} 1 ) > ( ¹ - Y k ) , при k e N . Если Y k e [ 0 -Me 1 ] , то 1 - Y k e [ 1 - Me 1 ,1 ] . Тогда число m берутся так, чтобы выполнялось неравенство

(1 - Me 2)( 1 + e ² )>1 , 0 <  e ,< M + M + 4M <  1 +А, ^ε 1 ^ε 1        ^ε 1      _{2 M         M}

2^2-...... < ^{2 +} м-^m >  m 0 ^: lob ⁾ 2 ( ^{2 +} м )•

Отсюда следует, что если выбираем число m такое, что m > m о , то будут выполняться неравенство R k + 1 > ^R k ^{-k e} N . Далее считается, что m^m о .

Пусть такой шаровой слой вида K (Rk-Rk+1)-i фиксирован, Cs: C(xs,asrs),xs = (xS,.,xns)-iсистема шаров из леммы 5.2. Обозначим через Cs(k)те шары, лежащие в множество K(Rk-Rk+1). Из неравенства 5.5 следует, что при    п < min {п 1 ,д 2 пМ5 М 6 п}

М ( k ) = { m ₁ ( k ) ,m ₂ ( k ) , ...} такое, что L ( k ) : { z e R ²: argz = m i ( k )( i = 1 -^ ) } не

существует счётноё множество mi (k )< mi+1 (k) ,mi+1 (k)-mi (k )< 2 h (p) и лучи пересекают круги Cs (k). Далее по математической индукции для множества K (Rk+1 -Rk+2) существует лучи L (k +1) такие, что L(k +1) nCs(k+1) /Я .Построенные последовательность сфер RkxS2, лучи L (k) это и есть разделяющие множества для меры р.

Если р -i вещественная мера из М , ( р ( r ) ) , то разделяющие множества для меры р — это разделяющие множества для меры | р | .

Теперь вводятся некоторые обозначения. Пусть р e М , ( р ( r ) ) , последовательность сфер R^S 1 и лучи L ( k ) разделяющие множества для меры μ .

A 1 ( k ) = { z e R ²: | z | e [ R 2 k - 1 ,R 2 k ] } -A 2 ( k ) = { z e R ²: | z | e [ R 2 k ,R 2 k + 1 ] |, B ₁ ( k ) = { z e R ²: argz ei j = 1 i w [ m ₂ j _{- 1} ( k ) ,m ₂ j ( k ) ]}, B ₂ ( k ) = { z e R ²: argz ei j = 1 i w [ m ₂ j ( k ) ,m ₂ j _{+ 1} ( k ) ] } ,

A ₁ =i k = 1 i ^ { A ₁ ( k ) П B ₁ ( 2 k - 1 ) j -A₂ =i k = 1 i ^ { A ₂ ( k ) П B ₁ ( 2 k ) ], A 3 =i k = 1 i ^ { A ₁ ( k ) П B ₂ ( 2 k - 1 ) j -A ₄ =i k = 1 i ^ { A ₂ ( k ) П B ₂ ( 2 k ) j.

Система множеств A. ( i = 1,2,3,4 ) будет покрывать пространство R 2 . Набор криволинейных                                 параллелепипедоввида

{ z g R ²:|| z ||g[ R k ,R k _{+ 1} ] ,argz e [ m j ( k ) ,m_{j + 1} ( k ) ] } , назовём паралле-лепипедами с соседними местами, если любая окрестность одного из них параллелепипеда будет пересекаться остальные. Заметим ещё, что во одно множество ^A i не входят параллелепипеды с соседними местами. Система множеств ^A i будем называть системой разделяющих множеств.