Построение кривой скорости в режиме тяги с использованием пакета расширения Simulink матричной лаборатории Matlab

Режим движения поезда определяется соотношением всех действующих на поезд сил. Анализ уравнения движения поезда (1) показывает, что в нормальных условиях эксплуатации возможны три режима движения поезда: тяга, выбег и торможение.

(1 + у ) ■ m ■ — = F ( V ) - W(V ) - B(V )

^dt                          (1)

где γ – коэффициент, учитывающий инерцию вращающихся частей; F ( V ) – характеристика силы тяги, определяется мощностью ЭПС; W ( V ) – силы сопротивления движению; B ( V ) – тормозная характеристика.

Рассмотрим режим тяги. Период тяги разделяется на периоды пуска подвижного состава и движения по автоматической характеристике. При пуске тяговые двигатели развивают наибольшую силу тяги. Сила тяги реализуется движущимися колесными парами. Поскольку в режиме тяги торможение не применяют, то dV _ F(V)- W(V) - B(V) dt         m (1 + у)

где B ( V ) = 0, m(1+γ) – величина постоянная, примем равную 1.

dV _ F ( V ) - W(V )

dt                                     (3)

При тяге, когда F ( V )> W ( V ) и, следовательно dV / dt> 0, подвижной состав движется ускорено. Если в режиме тяги F ( V )= W ( V ), то dV / dt= 0, и подвижной состав движется с установившейся скоростью. При F ( V )< W ( V ) подвижной

движется замедленно.

При движении подвижного состава возникают силы сопротивления движению. Результирующая сил сопротивления движению действует против направления движению подвижного состава.

W ( V ) = W k ( V ) + W в ( V ) + W кр + W ук   (4)

где W к ( V ) – сила сопротивления качению; W в ( V ) – сила сопротивления воздуха; W кр – удельное сопротивление от кривой; W ук – удельное сопротивление от уклона.

W k ( V ) = f G c                  (5)

где f – коэффициент трения качения; G с – вес состава.

На рис. 1 представлена зависимость коэффициента трения качения от скорости.

Аппроксимируем соотношение коэффициента трения качения f от скорости V и получим уравнение:

f ( V )=-2,058 10^-9 V ⁴ + 3,573 10^-8 V ³ –

– 1,102 10^-5 V ² + 1,118 10^-4 V + 1,293 10^-2

Тогда w.(V) _ C, ■ P ■ F ■ — в x в 2                     (7)

где V –скорость подвижного состава, C x – коэффициент аэродинамического сопротивления определяется по формуле:

С x = 0,46 +0,00225 l (8)

где l – длина состава, равная 60 м; P в – плотность воздуха, равная 1,293 кг/м, F – модель вагона, равная 3 м x∙2,65 м = 7,95 м².

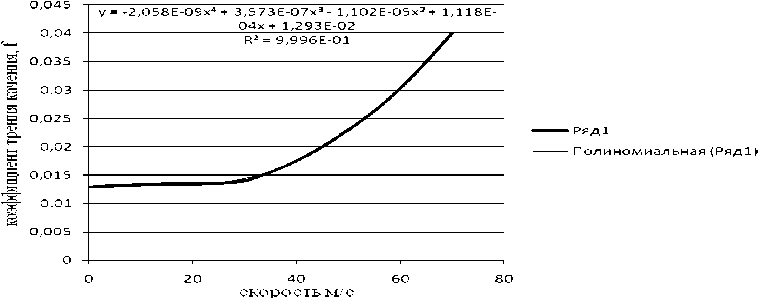
Рис. 1. Зависимость коэффициента трения качения f от скорости V

W кр = 0,45/ R кр        (9)

где R кр – радиус кривой.

W = —— ук 1000          (10)

где i - уклон в %.

На рис. 2 представлена динамическая модель построения кривой скорости в режиме тяги для высокоскоростной транспортной системы «Самара-Аэропорт-Толь-ятти». План и профиль трассы взяты из отчета ОАО «Сама-раэкотранс».

Используем метод конечных разностей – широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на разностные коэффициенты, что позволяет свести решение дифференциального уравнения к решению его разностного аналога, т.е. построить его конечно-разностную схему.

ay у -у

— = V ^{+ 1} V = F (V ) - dt      A t

- (W k ( V ) + W b (V ) + W p + W yk )

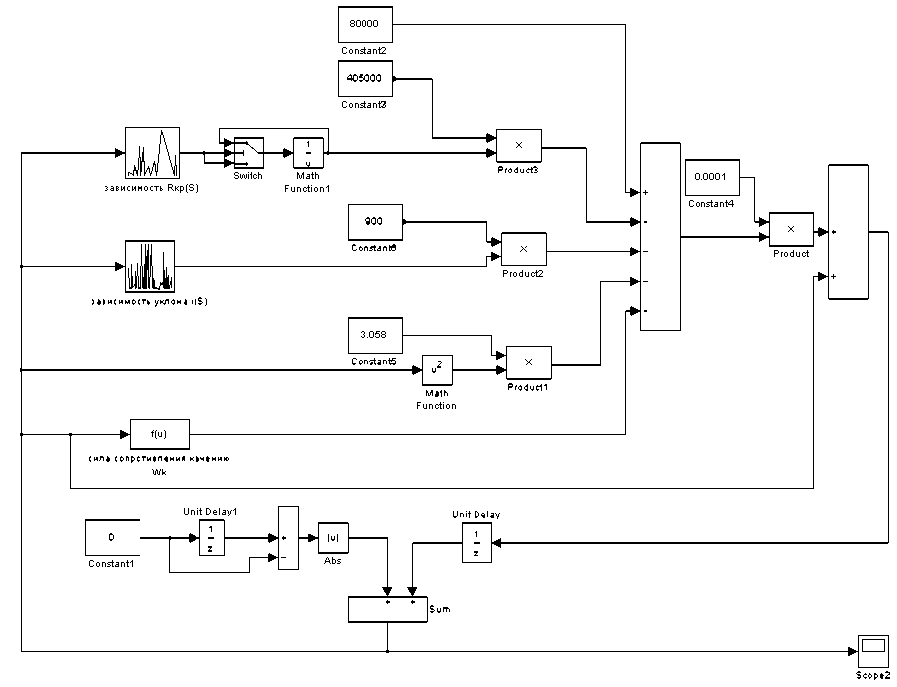
Рис. 2. Динамическая модель построения кривой скорости в режиме тяги

Интегрирование уравнения движения транспортного средства позволяет найти зависимость между скоростью движения, временем и пройденным расстоянием. Разобьем путь на малые участки ΔS и будем считать, что в пределах этих участков равнодействующая сила не зависит от скорости. Интегрируем уравнение движения транспортного средства и получаем выражение для скорости в начале i -го участка:

V t+1 =( F ( V )–( W k ( V )+ W в ( V )+ W кр + W ук ))Δ t + V t

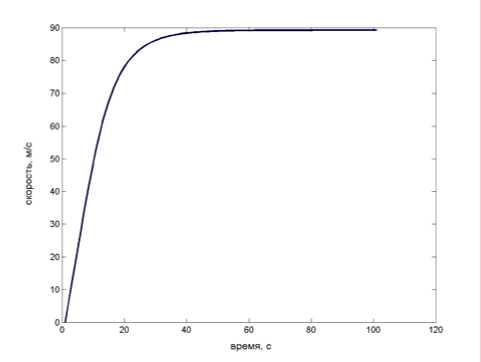
Рис. 3. Кривая скорости высокоскоростного подвижного состава

Результатом разработки модели является получение кривой скорости, развиваемой вы- сокоскоростным подвижным составом. На рис. 3 представлена кривая зависимости скорости от времени. Нахождение скорости и построение кривой является составной частью тягового расчета, необходимого для совершенствования проектирования системы электроснабжения высокоскоростной транспортной системы «Самара – Аэропорт – Тольятти». Система должна обладать высокой надежностью. Обеспечение высокой надежности требует относительно большой точности расчета параметров системы, особенно тех которые определяют ее прочность.