Построение квазиоптимальной по быстродействию и энергозатратам замкнутой системы управления электроустановкой

Для электротехнических процессов и установок актуальна задача повышения эффективности работы, так как 70 % вырабатываемой электроэнергии потребляют электроприводы, 10 % – электротермические установки1. Установки инфракрасного излучения, светотехнические и насосные установки являются энергоемкими в современных технологиях выращивания сельскохозяйственных культур в защищенном грунте [1]. Многие процессы и установки, особенно тепловые, имеют большую инерционность, то есть длительные динамические режимы перехода в устойчивое требуемое выходное состояние. Динамические режимы электроустановок как объектов управления с достаточной точностью описываются обыкновенными дифференциальными уравнениями, а в качестве управляющих воздействий служат ограниченные электрические переменные: обычно амплитуда, частота или скважность напряжения или тока.

В технических приложениях задачи оптимального перехода формулируются как задачи быстродействия, на минимум ресурсов (энерго- и ресурсосбережения) и точности (программного движения). Утверждается, что оптимальное энергосберегающее управление электрической сушильной камерой позволяет при определенных граничных условиях сэкономить до

60 % потребляемой электроэнергии [2]. Но известные алгоритмы оптимального быстродействия и энергосбережения отыскиваются в виде программного (то есть в функции времени) управления, не обеспечивают устойчивости конечного состояния объекта и в лучшем случае могут быть реализованы в форме нестационарной обратной связи.

Цель работы – применить особое оптимальное управление в качестве единого подхода для нахождения алгоритма управления с минимальными энергозатратами в функции состояний объекта, а также определить параметры и условия программного движения, обеспечивающие эффекты быстродействия и энергосбережения в устойчивой замкнутой системе управления электроустановкой.

Обзор литературы

Для решения оптимальных задач в технических приложениях используется принцип максимума Понтрягина, так как он, в отличие от классического вариационного исчисления, позволяет найти кусочно-непрерывное управление и учесть ограничения на переменные объекта2. Оптимальное управление отыскивается как функция зависящих от времени вспомогательных переменных, вводимых принципом максимума. Но в задачах быстродействия и на минимум ресурсов, нелинейных по координатам с линейным управлением, возможно существование особого режима, когда принцип максимума не устанавливает однозначной связи между оптимальным управлением и вспомогательными переменными3. Известные способы вычисления особого управления используют вспомогательные переменные непосредственно или с помощью скобок Пуассона [3; 4]. Найти решение для вспомогательных переменных, даже в функции времени, сложно, а для построения замкнутой системы в функции координат, позволяющей компенсировать действующие на объект возмущения, невозможно из-за неразрешимости двухточечной граничной задачи, к которой сводится решение оптимальной задачи. В задачах энергосбережения с квадратичным по управлению критерием особых режимов не возникает, но даже если оптимальное управление в функции времени будет получено, то синтез замкнутой системы осуществляется с помощью зависящих от времени и граничных условий обратных связей [2]. Тогда как для простоты технической реализации системы требуются стационарные обратные связи.

Для достижения предельного быстродействия или минимума ресурсов в задачах с линейным управлением необходимо кусочно-постоянное управление с максимально возможными амплитудами воздействия, что ведет к перерегулированию координат, а моменты переключения определяются нелинейными нестационарными поверхностями переключения или стыковки особых и неособых траекторий [5; 6]. Поэтому алгоритмы оптимального быстродействия неприменимы в задачах программного движения или оптимального по точности управления по достижению минимального отклонения от заданной траектории, особенно для объектов с длительными и частыми динамическими режимами перехода [7]. К тому же при оптимальном быстродействии не обеспечивается устойчивость конечного состояния в отличие от программного движения, гарантирующего ее на полубесконеч-ном интервале времени.

Что касается связи решений задач управления с критериями быстродействия и энергосбережения, то известны противоположные точки зрения: от их полного противопоставления, что объясняется необходимостью больших энергозатрат для увеличения быстродействия, до их полного совпадения, что справедливо при управлении в большом, когда при больших диапазонах задания начального и конечного состояний выхода минимальные энергозатраты получаются при максимально возможном управлении, то есть как в задаче быстродействия⁴ [8]. Сравнительные анализы оценки критериев быстродействия, энергозатрат и точности (программного движения) выполнены при управлении реальными тепловыми процессами в металлургии и теплоснабжении [9 ‒ 11]. На основе анализа особых, в смысле принципа максимума, режимов в задачах с линейным вхождением управления показано, что алгоритмы оптимальных управлений по быстродействию и на минимум ресурсов совпадают, если критерий на минимум ресурсов физически адекватно отражает поступление энергии в управляемый процесс [12].

Исходя из обзора литературы, можно говорить об актуальности разработки подхода по совмещенному определению алгоритма управления на базе принципа максимума и его особенностей в функции состояний объекта. Подход важен для построения устойчивой замкнутой системы управления.

Материалы и методы

Пусть математическое описание объекта управления (электроустановки) задается системой обыкновенных дифференциальных уравнений, нелинейных по координатам с линейным скалярным управлением в векторноматричной форме:

x = A ( x ) + B ( x ) U , (1)

где x e R n — вектор координат объекта; U – управление, 0 ≤ U ≤ 1; элементы вектор-столбцов A ( x ), B ( x ) непрерывны и дифференцируемы по x .

Задачами системы управления являются, во-первых, выработка ограниченного управления в функции времени или координат, переводящего объект из начального состояния x (0) в конечное x ( T) за незаданное или заранее заданное время и обеспечивающего минимум критерию оптимальности в виде интегрального функционала, учитывающего временные или энергетические затраты или отклонение текущей траектории от заданной (задача оптимального управления); во-вторых, последующая стабилизация конечного состояния в замкнутой системе со стационарными обратными связями (задача устойчивости или, в конечном счете, обеспечения работоспособности установки).

Для решения первой задачи оптимального управления с определением существования особого режима и вычисления особого управления в явном виде от координат и параметров нелинейного объекта, что необходимо на практике для синтеза замкнутой системы с обратной связью, применим аппарат условий общности положения (УОП) для нелинейных объектов. УОП был выведен в работе В. А. Олейникова для задач быстродействия и расширен для задач на минимум ресурсов в одном из наших исследований5.

Покажем применение УОП для нелинейных объектов в расширенном пространстве координат в задаче программного движения с критерием

I = f 0 ( x n TP ⁽ t ^ x n ⁽ t ) ) ² dt ’ ⁽²⁾

учитывающим квадратичные отклонения текущей выходной координаты объекта от требуемой [13]. Задача (1), (2) является нелинейной по координатам, поэтому в ней при использовании принципа максимума, даже для линейных объектов, возможно возникновение особых ситуаций, если на некотором интервале времени t е [ t 1 ,1 2 ] :

d ( v , в ( x ) ) dt^k

= 0, k = 0,1,2,...,

где у - вектор вспомогательных переменных, вводимых принципом максимума, из уравнения dy . faA(x). aB(x)U)T„ dt v ax ax v

Условие существования особого режима (3) требует анализа вспомогательных переменных ψ(t). Чтобы его избежать, в аппарате УОП вычисляются векторы Bj, j = 2, ..., n + 2, по рекуррентному соотношению:

B1 (x ) = B (x),

5 B j _ _x dU

B i =

5 U dt

—

⁵ A ( x VВ ( x ) U )      ⁵ B j _ , dx

1 В

5 x        5 x   J ⁷      5 x dt

^x n TP ⁽ t ) " x n ⁽ t ) ) ^{2 2}

A (x)

I                    7

' 0 '

B(*^B0*)

После образования матрицы D_{n +2} размером ( n + 2) ∙ ( n + 2) из векторов ( B ₁ … B_{n+ 2}) и приравнивания к нулю определителя det D_{n +2} = 0 находятся уравнения особых траекторий и особых управлений, множество которых можно расширить путем приравнивания к нулю функциональных элементов матрицы D_{n +2}, так как при этом тождественно выполняются условия особого режима (3).

При исследовании функциональных элементов матрицы D_{n +2} учитываются не только особые режимы задачи программного движения, но и задач быстродействия и на минимум ресурсов с линейным управлением, так как в матрицу D_{n +2} вложены матрицы

D

( Ь²¹  b ^{2 2} 'I ^и ^=

V 31   ^и32 7

b 21    b 2 2    b 23 '

V ^b3i    b 32    Ь з з )

проверяемые в этих задачах. Таким образом, свойства оптимального по быстродействию управления являются характерными для объекта и сохраняются при других критериях оптимальности, а в целом проверка УОП позволяет выявить общие свойства оптимального управления в задачах быстродействия, на минимум ресурсов и программного движения.

Интегральный критерий энергозатрат для большинства электротехнических устройств имеет вид

I - T U ² dt .            (5)

Как и М. Атанс и П. Фалб, предположим, что « U ( t ) - скаляр, пропорциональный напряжению или току, тогда величина U ²( t ) пропорциональна мощ-

T ₂

ности, а  U dt пропорционален энер- t0

гии, израсходованной на интервале [ t ₀, T ]»⁶. Такой критерий энергозатрат используется в большинстве работ, но иногда, как заметил Ю. П. Петров,

«в задачах частотного управления рекомендуется использовать критерий

^TU 1,5 dt , t 0

так как потери на гистерезис и вихревые токи пропорциональны соответственно первой и второй степени частоты электрического сигнала»7.

Задача энергосбережения (1), (5) нелинейна по управлению, поэтому особых режимов в ней не возникает, и при ее решении можно однозначно выразить оптимальное программное управление, как отмечает В. И. Ловчаков, через вспомогательные переменные с помощью принципа максимума или множители Лагранжа в классическом вариационном исчислении или методом динамического программирования [2].

Чтобы исключить трудоемкую операцию нахождения дополнительных переменных, предложен способ поиска дифференциального уравнения для оптимального управления в функции координат объекта, основанный на применении аппарата УОП для нелинейных объектов, для чего производится приведение исходной задачи (1), (5) к редуцированной задаче с линейным вхождением управления, в которой возможно существование особого режима. Как мы писали в одной из предыдущих работ, «УОП для нелинейных объектов в расширенном пространстве координат R n +2 применяются к редуцированной задаче энергосбережения (1), (5):

^Х = y , о

< x = A ( x ) + B ( x ) x 0 , X n ₊i = ( x 0 ) 2 .

Из выражения для детерминанта и элементов матрицы Dn+2 = (B 1 B2 .. Bn Bn+i Bn+2), вычисленных с учетом замены U на у по рекуррентному соотношению (4), в общем случае получается множество особых управлений y и его производных по времени в функции координат редуцированного объекта det Dn+2 = Fo (x, x0, y, y,...) = 0, а после обратной замены переменных управления в редуцированной задаче на переменные управления в исходной задаче k-1           k x0 = U,      У = U, k = 1,2,3,^

dtk-1 л dtk получается дифференциальное уравнение для оптимального программного управления в функции координат исходного объекта»8. А именно:

F ( x , U , U , U , ^ ) - 0.

Постоянные интегрирования в общем решении системы дифференциальных уравнений объекта (1) и дифференциального уравнения для оптимального программного управления (6) определяются из решения двухточечной граничной задачи для заданных состояний выхода объекта и его ( n - 1) производных в начальный и конечный фиксированный момент времени T. Получаемое управление и соответствующие фазовые траектории являются трансцендентными функциями от времени, и замкнутая система может быть реализована с помощью нелинейных функциональных преобразователей, нестационарной обратной связи или путем аппроксимации траекторий и управления [2; 14–16].

Что касается второй задачи, стабилизации, то алгоритмы быстродействия и энергосбережения не обеспечивают устойчивость конечного состояния. Алгоритм программного движения может гарантировать устойчивость, поэтому для его эффективности по быстродействию и энергосбережению предлагается ввести в желаемый закон движения выходной координаты объекта такой параметр т, который противоречиво влияет на время переходного процесса T и амплитуду управляющего воздействия U. Таким параметром, исходя из физических соображений по второму закону Ньютона, может быть мера инерционности процесса. Если взять апериодическое звено первого порядка с дифференциальной связью тх = U - x, то T прямо пропорционально τ и составляет (3÷4)τ, а амплитуда U обратно пропорциональна τ. Тогда выбор параметра τ дает эффективные решения для значений T и U, так как нельзя уменьшить значение одного, не увеличивая значение другого9. Найти оптимальные значения быстродействия T и энергии E как интеграла от квадрата управления U можно из экстремума энергии E по параметру τ при переходе из начального состояния xнач в конечное xкон за время T по условию

8 E ( х _нач, х _кон, т , U , T ) ₌ 0. ₍₇₎ 8т

Если при вычисленном по (7) т _опт выполняются ограничения по управлению и координатам, то в задаче программного движения с критерием (2) при

-t -t/ Л х (А = х е7%™ + х I 1- е/т™ I (8) n тр нач кон обеспечивается квазиоптимальное (в смысле локальной оптимальности, в отличие от глобальной оптимальности при оптимальном программном управлении) управление по быстродействию и энергозатратам.

Устойчивость квазиоптимальной системы можно проверить по функции Ляпунова методами качественной теории дифференциальных уравнений или критериев устойчивости [17]. Структура замкнутой квазиоптимальной системы для линейных объектов управления содержит линейные стационарные обратные связи с коэффициентами передачи, зависящими от параметра τ _опт.

Результаты исследования

Покажем применение предложенных на основе особого оптимального управления подходов в решении задач оптимального и квазиоптимального управления линейным объектом, динамика которого описывается линейным дифференциальным уравнением

Том 32, № 2. 2022

X i - U - X i , ⁽⁹⁾ где коэффициент усиления и постоянная времени равны 1, на управление и состояние наложены ограничения 0 <  U < 1, 0 <  x 1 < 1. Граничные условия x _1нач = 0, x _1кон = x к . Выбор объекта объясняется меньшей громоздкостью вычислений и большей прозрачностью результатов для оценки вычислительных, временных и энергетических затрат и оценки устойчивости получаемых решений.

Задача оптимального энергосберегающего управления

УОП в расширенном пространстве координат R 3 применяются к редуцированной задаче

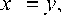
< Х 1 = x - Х 1 , . x = ( x ⁰ ) 2 .

Вычисляются векторы B j , j = 1, 2, 3, по соотношению (4), и образуется матрица D 3 :

	( 1	0	0 )
D 3 = ( B 1 B 2 B 3 ) =	0	- 1	- 1
	1 0	- 2 x 0	- 2 У J

Из det D3 = 0 определяется особое управление в редуцированной задаче y - x0 = 0, после перехода к оптимальному управлению в исходной задаче решается система дифференциальных уравнений f x1 = U - x1,

[ U = U .

Общим решением системы дифференциальных уравнений объекта и управления являются

' Х 1 ( t ) = C 1 e + C 2 e - t , U ( t ) = 2 C e t .

■ к V

I = f 0

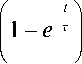
- x  dt ,

J

Постоянные интегрирования определяются из граничных условий. Пусть x 1 (0) = 0, x 1кон = 0,5 при T = 2. Графики переходных процессов для координаты x 1* ( t ) = 0,069( e + e t ) и оптимального программного управления U * ( t ) = 0,138 e t приведены на рисунке 1. При этом затраты энергии E = J²( ^ * ( t ) )² dt = 0,52, что на 30,7 % меньше, чем энергозатраты в разомкнутой системе с управлением U ( t ) = 0,5 на интервале времени t ∈ [0, 3]. Но аналитически выразить U ^* через x ₁^* из-за трансцендентности невозможно, к тому же нужно будет дополнительно решать задачу стабилизации конечного состояния.

Задача квазиоптимального управления

Рассмотрим задачу программного движения для объекта (9) с критерием учитывающим переход из x1(0) = 0 в x 1(T ^ да) = xк c минимальными квадратичными отклонениями от переходного процесса апериодического звена тх = U - х с U = xк.

Применим УОП в расширенном пространстве координат R 3 к поставленной задаче

’ x = 1,

Х 1 = U - x 1 ,

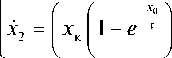
— x 1

После вычисления векторов B j , j = = 1, 2, 3, по соотношению (4) образуем матрицу D 3 = ( B 1 B 2 B 3 ):

( 0 0   0 )

D 3 = ¹

( 0

1 b ₃₂

ъ и33 у

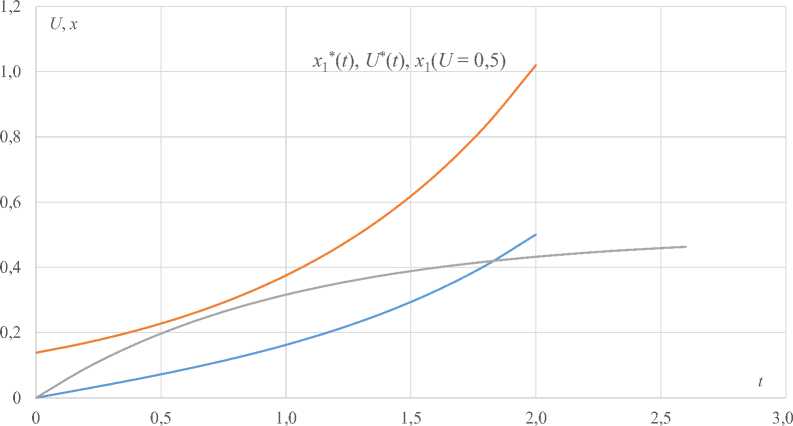
----x 1 *( U *) ---- U * ---- x 1 ( U )

Р и с. 1. Траектории x 1* и U * оптимального программного управления

F i g. 1. Trajectories x 1* and U of optimal programmed control

Electrical technologies and equipment                                                           287

из элементов которой f     - x0 )

b32 = 2xK 11 - e T I - 2x 1, x0

I I    - x0 II        T b„ = 2 x 1 - e T - x + 2 xe--2U + 2x

33              Ki                                             1

II JI T определяются в функции времени особая траектория, совпадающая с желаемой по критерию (10), и особое управление, являющееся оптимальным в задаче программного движения

L - t Г 1

U ( t,x_к, т ) = x _к I 1 + e ^т I

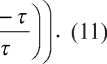
После исключения времени в последних находится управление в замкнутой системе, линейно зависящее от координаты x 1 :

U ( х , , х„г ) = x - "  x ^{1 ( 1} " ¹ > . (12) т

На рисунке 2 приведена графическая иллюстрация связей между переменными в уравнении (12). Из уравнений (11) и (12) следует, что начальная амплитуда управления U(x1(0) = 0) обратно пропорциональна параметру τ. При τ ≤ τмин (рис. 2) начальный участок управления в программном движении, как в задаче быстродействия, принадлежит ограничению на управление U = 1 и чем больше xк, тем при больших τмин выходим на это ограничение, что следует и из связи U (x 1 (0) = 0) < 1 = x^. Это означает, ^мин что при больших диапазонах заданных граничных условий в программном движении исчезает эффект энергосберегающего управления и оно приближается к оптимальному управлению по быстродействию [2].

Величина энергии, затрачиваемой на переход из x ₁(0) = 0 в x _к за время T = = 3 τ при управлении (13), равна

Tau=∞ Tau=2 Tau=1 Tau=opt Tau=min Tau

Р и с. 2. Связи переменных в программном движении

F i g. 2. Relationships of variables in the program motion

288                                            Электротехнологии и электрооборудование

^E Ч 0 (U ( t ’ x - ’ ^T ) ) ² dt ⁼ x *

( 3 т ² + 2 т + 2 т

.

Минимум энергии Е по параметру τ определится из условия

8 E ₌ x 2 ^{( 3 t 2} " 1 ) S t     ^k   2 t²

= 0,

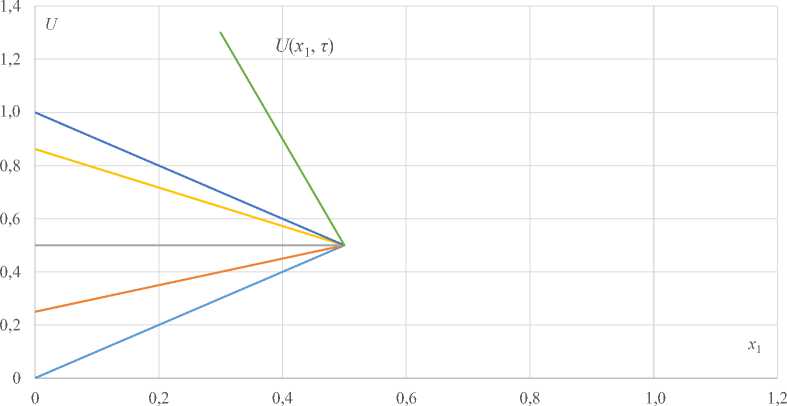
откуда т _опт = 0,58. Отметим, что полученный параметр т опт не зависит от x _к. Зависимость энергии E от параметра τ при x = 0,5 показана на рисунке 3. Спадающий в положительном направлении т участок функции E ( т ) характеризует эффективные по быстродействию и энергозатратам режимы [18]. Оптимальное в программном движении решение с т _опт = 0,58 дает 9,3 % относительной экономии энергии, по сравнению с управлением в разомкнутой системе с τ = 1, что существенно ниже 30,7 % экономии энергии при оптимальном программном управлении, но при программном движении обеспечивается устойчивость конечного состояния.

При выборе x _к >  т _мин, то есть, когда т м _ин >  т _опт (рис. 2, 3), переходим на восходящую ветвь функции E ( т ), быстродействие и энергозатраты непротиворечивы, их эффекты хотя и снижаются, но сохраняются по сравнению с т = 1. Отметим, что выбор меньшего т дает больший эффект по быстродействию или производительности установки, чем эффект по энергозатратам, что следует из слабой вогнутости кривой E ( τ ). При больших x _к наблюдается более выраженный экстремум в зависимости E ( τ ). Графики переходных процессов в программном движении с τ _опт = 0,58 и τ = 1 для x _к = 0,5 приведены на рисунке 4.

Структура позиционной системы управления, квазиоптимальной по быстродействию и энергозатратам, полученная из (12) с τ _опт и технически просто реализуемая, приведена на рисунке 5. Если граничные условия x _к >  т _опт или ^т мин >  ^т опт , то x к >  ^т опт ^{или т} мин >  ^т опт , то ^для ограничения амплитуды управления введено звено насыщения с линейным участком единичного наклона в диапазоне [0, 1].

1,8

1,6

1,4

1,2

1,0

0,8

0,6

0,4

0,2

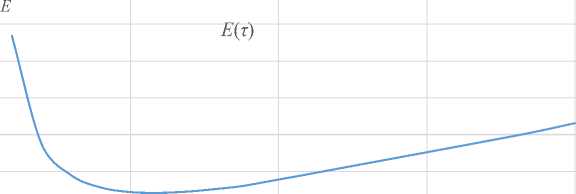
τ

0,5                     1,0                     1,5                     2,0

2,5

E

Р и с. 3. Зависимость энергии E от параметра τ в программном движении

F i g. 3. Dependence of the energy E on the parameter τ in the program motion

Electrical technologies and equipment                                                           289

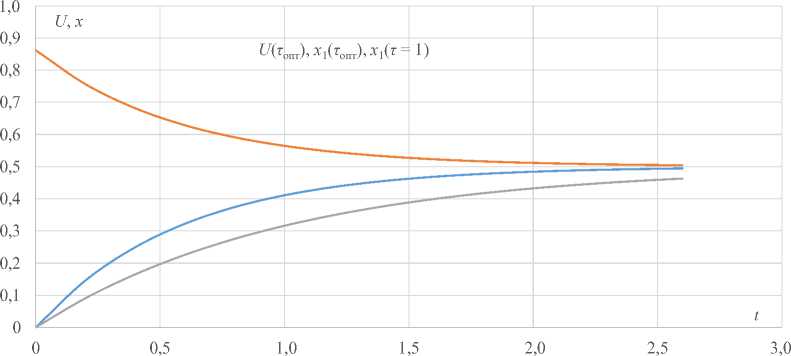
---x ₁(TAUonm) --- I (TAI опт) --- x i (TAU=1)

Р и с. 4. Графики переходных процессов в программном движении

F i g. 4. Graphs of transients in the program motion

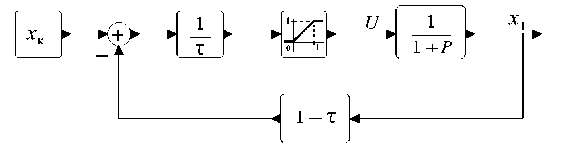
Р и с. 5. Структура позиционной системы управления

F i g. 5. Structure of the positional control system

Непосредственное применение результатов данной работы можно показать на примере оптимального энергосберегающего управления сушильной камерой, приведенного в работе В. И. Ловчакова [2]. Хотя поведение объекта описывается дифференциальным уравнением второго порядка, для конкретных граничных условий можно построить адекватную модель первого порядка с помощью метода наименьших квадратов по кривой переходного процесса или частотных характеристик. Далее, применяя пошагово методику данной работы, можно в замкнутой устойчивой системе получить квазиоптимальное по энергозатратам и быстродействию управление, обеспечивающее 10-30 % экономии электроэнергии и в 1,5–2,0 раза большее быстродействие при корректном сравнении с управлением в разомкнутой системе, соответствующим конечному значению выходной координаты.

Обсуждение и заключение

В целом предлагаемый подход к построению оптимальных систем по критериям быстродействия, энергосбережения и точности на основе УОП для нелинейных объектов в расширенном пространстве координат показал свою результативность и эффективность. Квазиоптимальность по энергозатратам и быстродействию в устойчивом динамическом режиме достигается тем, что в задаче программного движения выполняется минимизация энергии по параметру программного движения, противоречиво влияющему на время переходного процесса и амплитуду управляющего воздействия. Формали-зованность подхода предполагает его использование в задачах многокритериальной оптимизации и системах автоматизированного проектирования.

В дальнейшем предлагается применять подход к объектам большей размерности с учетом структурно-функциональных особенностей, различных представлений дифференциальных уравнений объекта в нормальной форме или с отражением физической сущности. Не решена задача достижения предель- ного энергосбережения, получаемого при оптимальном программном управлении, с алгоритмом и структурой устройства определения частных решений и обеспечивающего устойчивость замкнутой стационарной системы.

Результаты работы могут быть использованы при исследовании динамических режимов электроустановок в промышленных и сельскохозяйственных тепловых процессах (жилые и нежилые помещения, теплицы, печи, сушильные камеры, автоклавы); в светотехнических установках; на транспорте в автономных электроприводах; в мехатронных и робототехнических устройствах, например для обеспечения мягкого пуска электроприводов, и в других процессах и установках [19; 20].

С. 148-163. URL: https://joumals.eco-vector.com/1991-8542/article/view/19977/16230 (дата обращения: 25.01.2022).

Поступила 25.01.2022; одобрена после рецензирования 11.02.2022; принята к публикации 03.03.2022

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

Electrical technologies and equipment

Submitted 25.01.2022; approved after reviewing 11.02.2022; accepted for publication 03.03.2022

All authors have read and approved the final manuscript.