Построение математических моделей в задачах обработки экспериментально-статистической информации

Одна из важнейших проблем при проведении научных и учебных исследований в условиях интегрированного комплекса сетевых автоматизированных лабораторий (ИКСАЛ) – это моделирование, центральным звеном которого является построение математической модели (ММ) исследуемого объекта [1-3]. Независимо от способа построения модели важной частью её структурной и параметрической идентификации остаётся обработка экспериментально-статистической информации, получаемой либо в лабораторных условиях, либо при натурных испытаниях, либо с функционирующего объекта.

Цель настоящей работы: разработка методов и алгоритмов структурно-параметрического синтеза математических моделей, создание единого комплекса программ, обеспечивающего повышение эффективности обработки экспериментально-статистической информации в ИКСАЛ.

Методология построения математических моделей по экспериментальным данным. Предлагается единая система структурно-параметрического синтеза математических моделей в задачах обработки экспериментальных данных в ИКСАЛ, основу которой составляют три следующих принципа [1, 2].

• •    Систематизация ММ по видам преобразования координат.

• •    Многоуровневый синтез пакетов функциональных зависимостей.

• •    Получение состоятельных, несмещённых и эффективных оценок ММ в преобразованных координатах.

В работе ставится задача создания системы автоматизированного выбора структуры нелинейной модели, что определяет необходимость автоматического подбора нужной функциональной зависимости по совокупности экспериментальных данных. Предлагается выбор моделей проводить на базе системы функций с заданным набором преобразования координат. Под функционально-полным набором математических моделей будем понимать совокупность моделей, объединяющих все возможные математические модели, которые могут быть синтезированы на заданном наборе нелинейных преобразований координат и одновременно среди которых нет хотя бы одной пары функций, получаемой с использованием одних и тех же преобразований координат [2]. Предложенный метод структурно-параметрического синтеза моделей по видам преобразования координат состоит в формировании функционально-полных наборов пакетов ММ по заданным видам функциональных преобразований ψ( х ) и φ( у ) определённого x и результативного y признаков

>^ у = ф " 1 ( а о + а^( x ) )

Ф ( У )

x

и в организации для каждого пакета множества линейно-зависимых ММ, наиболее полно отражающих свойства исследуемого объекта.

Ф - 1 ( a o + a i ^ ( x ) ) = { f i ( a o + a l x ) } ,

Таким образом, предлагаемый метод синтеза ММ может быть представлен следующими преобразованиями

^ф( y )' v ( x )

"^ У = { ft ^{( a}0 + ^ai x

При автоматизированном синтезе функционально-полных наборов линейно-независимых ММ с использованием n видов преобразования координат возможно построение n ² однофакторных моделей. С целью расширения набора функций и возможностей учёта различных нелинейностей в моделях предлагается проводить синтез моделей с многократным использованием одних и тех же видов преобразования координат:

У = Ф - 1 ( ... ф - ¹ ( ф - ¹ ( a o + a l

Здесь n и m – количество уровней преобразований результативного и определённого признаков.

Одной из основных проблем построения моделей с использованием известных методов определения параметров моделей в преобразованных координатах является неэффективность получаемых оценок ММ. Для обеспечения построения ММ в преобразованных координатах разработан метод реверсивного преобразования координат (РПК) [2], обеспечивающий эффективность, состоятельность и не- смещённость оценок ванных координатах.

моделей в непреобразо-

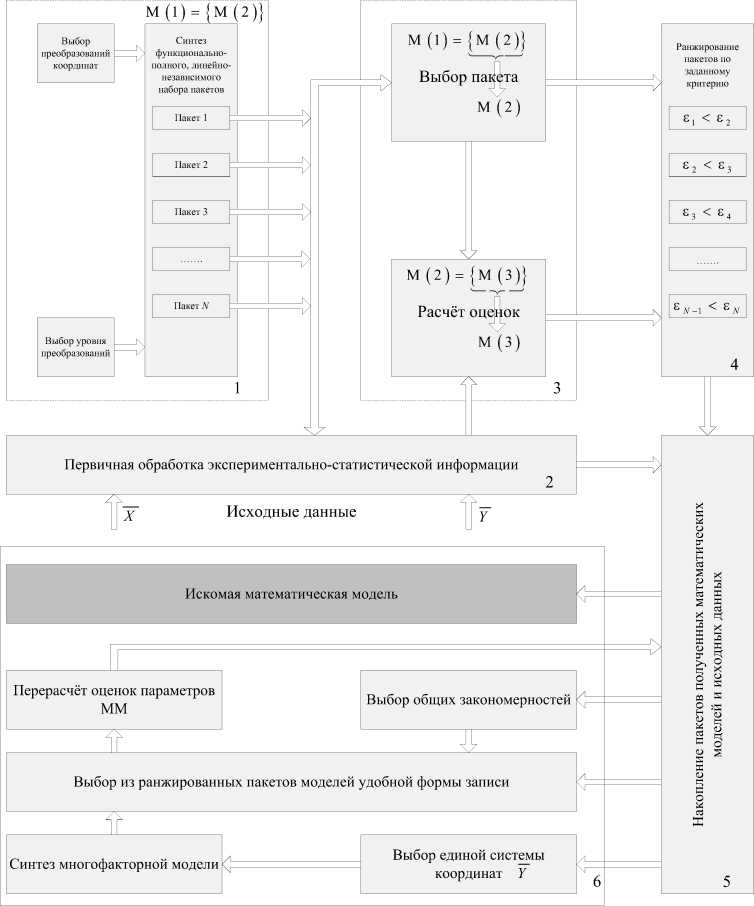
Рис. 1. Схема построения стохастических математических моделей

Систематизация математических моделей. Первый принцип предложенного подхода заключается в систематизации пакетов функций с использованием простейших видов преобразований координат результативного и определённого признака. Такой подход сводит процесс выбора к сравнению ограниченного и в то же время функционально полного набора функций, обеспечивает эффективность сравнительного анализа моделей. Если в основу систематизации и приведения ММ к линейному виду положить прямо пропорциональное Х=х , логарифмическое Х =ln x и обратно пропорциональное X =1/ x преобразования, то для двух переменных при однократном их преобразовании можно получить девять видов функций. При пяти преобразованиях, взятых в качестве основных, можно синтезировать набор из 25 линейно независимых функций [2].

Схема построения стохастических математических моделей. Структурная схема построения математической модели на базе предложенных принципов представлена на рис. 1 и включает в себя следующие процедуры:

• 1.    Синтез функционально-полных пакетов ММ. Наборы пакетов моделей задаются видом и уровнем преобразования координат.

• 2.    Предварительная обработка экспериментально-статистической информации, включающая нормировку, сглаживание и преобразование исходных данных в соответствии с выбранными видами и уровнем координатных преобразований.

• 3.    Структурная и параметрическая идентификация математических моделей.

• 4.    Ранжирование пакетов математических моделей по заданному критерию (минимум среднеквадратического отклонения или относительной ошибки).

• 5.    Накопление пакетов полученных математических моделей и исходных данных.

• 6.    Получение однофакторных и многофакторных моделей удобной формы записи, описывающих общие закономерности рассматриваемых явлений.

Предложенные принципы систематизации и многоуровневого преобразования координат – основа синтеза функциональнополных линейно-независимых наборов пакетов математических моделей в первом блоке. Во втором блоке производится преобразование экспериментальных данных в соответствии с заданными видами и уровнем преобразования координат. Использование в третьем блоке метода РПК обеспечивает получение состоятельных, несмещенных и эффективных оценок при структурной и параметрической идентификации математических моделей. Накопленная в блоке 5 экспериментально-статистическая информация и ранжированные в блоке 4 пакеты моделей используются на заключительном этапе построения математических моделей в блоке 6. В блоке 6 решаются четыре основные задачи:

• •    получение однофакторной математической модели удобной формы записи (выбор из пакета линейно-зависимых моделей – модели удобной формы записи);

• •    выбор единой системы координат для результативного признака и синтез многофакторных моделей по совокупности однофакторных экспериментов;

• •    выбор общих оценок параметров моделей по совокупности разнородных экспериментов с однотипными переменными;

• •    пересчет оценок параметров математических моделей для выбранной структуры и формы.

На основе представленной структурной схемы разработан программный комплекс структурно-параметрического синтеза математических моделей. Результаты исследования, полученные методами РПК, последовательного спуска с полиномиальной аппроксимацией (ПСПА) и методом наименьших квадратов (МНК) математических моделей вида, на основе экспериментальных данных, приведены на рис. 2 и в табл. 1.

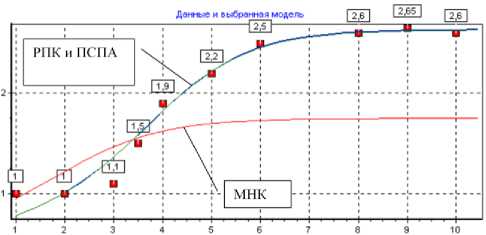
Рис. 2. Графики модели Y=1/(Ln(Ln(А0+А1* *Exp(1/(Exp(X)))))) с параметрами А1, А0, рассчитанными тремя методами МНК, РПК, ПСПА

Поскольку процедура выбора вида математической модели предполагает сравнение между собой большого числа линейно независимых функций, а, следовательно, и вычисление параметров для каждой ММ в процессе структурной идентификации, использование методов многомерной оптимизации для определения оценок параметров оказывается дорогостоящим с точки зрения вычислительных затрат. Кроме того, при некоторых комбинациях результативного и определённого признаков такие методы требуют установки дополнительных условий, что затрудняет их программирование.

Таблица 1. Параметры рассчитанных математических моделей

Название метода	Модель	Ост. дисп.	Сред. зн. от. ош. на инт.
МНК	Y=1/(Ln(Ln( – 20,146+26,024*Exp(1/(Exp(X))))))	0,421	0,58094
РПК	Y=1/(Ln(Ln( – 67,972+72,280*Exp(1/(Exp(X))))))	0,017	0,11694
ПСПА	Y=1/(Ln(Ln( – 68,244+72,559*Exp(1/(Exp(X))))))	0,016	0,11655

Предлагаемый способ расчёта оценок параметров ММ свободен от вышеперечисленных недостатков. Так, например, трёхуровневый выбор ММ с использованием метода расчёта оценок ПСПА для 20 экспериментальных точек при применении ЭВМ класса P5/16 занимает 1 час 40 минут, в то время как расчёт с применением предложенного метода – 20 секунд, что сравнимо со временем, затраченным на поиск при использовании метода наименьших квадратов в преобразованных координатах – 18 секунд. Вместе с тем, как показывают расчёты, во всех случаях оценки, полученные с использованием предлагаемых методов, близки к точным и значительно превосходят по точности оценки, получаемые методом наименьших квадратов в преобразованных координатах, что свидетельствует об их высокой эффективности.

Проведенные исследования предложенных подходов и принципов, разработанных методов в ИКСАЛ показали их высокую эффективность и преимущества перед существующими методами.