Построение математической модели физически нелинейных колебаний многоэтажного каркаса

Введение. Построение аналитических решений при колебаниях строительных конструкций с учётом упругопластических свойств материала требует использования более сложных инструментов анализа, нежели те, которые применяются при изучении упругих колебаний. В подавляющем большинстве анализ колебаний систем с нелинейной восстанавливающей силой проводится численными методами шагового интегрирования [1–3]. Однако данные методы не позволяют проводить полноценный динамический анализ расчётных моделей сооружений, поскольку существуют проблемы выбора шага интегрирования, сходимости и устойчивости шаговых методов [3, 4].

В реальных условиях колебаний в нагруженных элементах конструкции наряду с текучестью и разгрузкой происходят повторные нелинейные процессы текучести и разгрузки, что затрудняет проведение надежной оценки динамической реакции с помощью численных методов. В работах последнего времени всё чаще отмечается недостаточность теоретических исследований в области колебаний конструкций с нелинейной восстанавливающей силой [5].

В настоящей работе предложена математическая модель упругопластических колебаний многоэтажного каркаса с динамической восстанавливающей силой (ДВС), изменяющейся по билинейному закону c разгрузкой. Диаграмма деформирования (ДД) «восстанавливающая сила – относительное перемещение» может содержать несколько гистерезисных петель для учета повторных текучестей и разгрузок в этажах каркаса [6].

Поскольку ДД представляет собой кусочнолинейную аппроксимацию, то весь процесс нелинейной динамической реакции по времени разбивается на отдельные (последовательные) интервалы t ∈ [ti, ti+1] (i = 0, 1, 2, …), внутри которых па- раметры расчетной модели (элементы матриц масс, жесткости и демпфирования) постоянны. Это обеспечивает последовательное построение динамической реакции по схеме упругого решения и является отражением того факта, что на данных интервалах (называемых далее квазилинейными) уравнение движения в математическом плане рассматривается как обыкновенное дифференциальное уравнение (ОДУ) с постоянными коэффициентами. Моделирование циклических процессов нелинейного деформирования является важной предпосылкой для создания удобной расчетной схемы в рамках теории временного анализа [6, 7]. Некоторые вопросы физически нелинейных колебаний рассматривались в работах [8, 9].

В качестве расчетной динамической модели (рис. 1) была принята сдвиговая модель плоского каркаса, в котором перекрытия этажей считаются абсолютно жесткими, стойки каркаса несжимаемыми и нерастяжимыми, деформирование колонн происходит в поперечном направлении. Таким образом, число степеней свободы n равно количе-

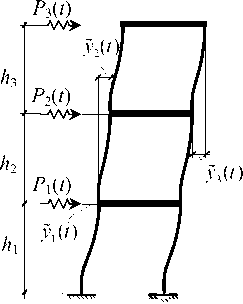
Рис. 1. Расчетная динамическая модель 3-этажного каркаса ству этажей каркаса. Динамическая нагрузка Pj(t) приложена в уровне перекрытий этажей; yi (t) - относительные перемещения j-х этажей каркаса.

Уравнение движения системы с n степенями свободы (1а) на любом квазилинейном интервале времени с начальными условиями (1б) в матричном виде записываются так [6, 7] ( t е [ t i , t_i+1 ]):

MY ( t ) + C i Y ( t ) + R ( t ) = P ( t ), (а) !           (1)

Y(tо) = Yo, Y(to) = Y,      (б)U где M = diag(m1, ..., mn), Ci = Cf еMn (R) - матрицы масс и демпфирования; Y(t) = {yj(t)}, R(t) = {Rj(t)}, P(t) (j = 1,…, n) – векторы перемещений, динамических восстанавливающих сил (ДВС) и внешней нагрузки; j – номер этажа; t0 – время начала действия динамической нагрузки. Параметры матрицы масс считаются неизменными на всем интервале реагирования системы.

Для построения закона «ДВС – относительное перемещение»: R j ( t )~ y j ( t ) рассмотрим упругопластическую работу расчетной модели в j -м этаже каркаса. Каждый полуцикл диаграммы имеет три участка деформирования: нагружение, упрочнение и разгрузка. Первому полуциклу соответствуют участки ОА, АВ и ВС (рис. 2).

Аналитические зависимости ДВС в 1-м полуцикле

Рассмотрим построение ДВС на каждом из трех участков. Номер полуцикла у ДВС и перемещений обозначается далее верхним индексом.

Участок нагружения ОА . На участке ОА ДВС имеет вид:

R j ‘’( t ) = R ®( t ) = tga _y . y j ( t ),                  (2)

где R e ⁽¹ j ⁾ ( t ) – квазилинейная восстанавливающая сила в 1-м полуцикле ДД.

Участок упрочнения АВ . Здесь воспользуемся вспомогательным построением с помощью прямой Om || AB (рис. 2). Тогда ДВС будет иметь вид:

R ⁽ j ¹⁾ ( t ) = R e ⁽ j ¹⁾ ( t ) + R u ⁽¹ j ⁾ ( t 1 ) =

= tg P j ' j t ) ⁺ ^ У о j ,                         ⁽³⁾

где

R e} ⁾( t ) = tg P j-y ( t ), R < *^ ( 1 1 ) = A y 0 j ,

• A , = tg a , - tg P , ,

• t 1 – время начала нелинейной работы (текучесть) стоек j -го этажа (соответствует точке А на ДД).

Участок разгрузки ВС . На данном участке стойки j -го этажа получают пластические (необратимые) деформации вследствие появления остаточных перемещений y ⁽ _p ¹ _j ⁾ . Поэтому ДВС будет содержать остаточную составляющую R ⁽ p ¹ j ⁾ ( t ₂ ):

R j4 1 ) = R^⁾( t )- R ⁽1) (t 1 2 ),

где

R ej^{1 (} t )=tg ^a j • ^yi ⁽ t ), R pj ⁽ t 2 )=tg ^a j • y pj ,   ⁽⁶⁾

• t ₂ – время завершения нелинейной работы (начало разгрузки) стоек j -го этажа (соответствует точке B на ДД).

Выражениям (3), (5) дана графическая иллюстрация на рис. 2.

Аналитические зависимости ДВС во 2-м полуцикле

При составлении зависимостей для ДВС во 2-м полуцикле (рис. 3) необходимо определить положение точки D на ДД и дать несколько определений.

Точка D определяется в соответствии с принципом Мазинга [10], утверждающим, что в 1-м цикле переход к неупругому деформированию происходит после упругого деформирования на величину 2 а Т , где а _Т - предел текучести материала. В координатах, принятых на ДД, величина 2 а _Т

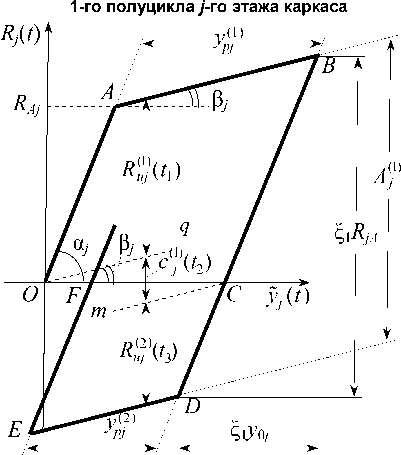
Рис. 3. Диаграмма деформирования для первых двух полуциклов j -го этажа каркаса

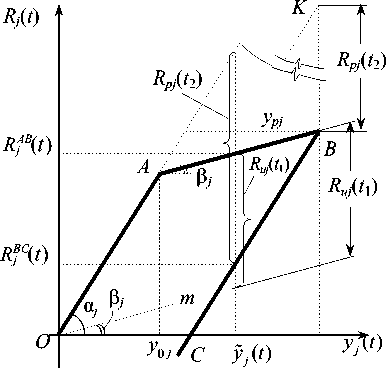
Рис. 2. Диаграмма деформирования соответствует удвоенному значению 2RAj (рис. 3), что составляет ординату 2RAj = ^1 у0,tga, (^1 = 2). Отсюда

A = у о А                           (7)

С другой стороны, эта величина заключена между параллельными прямыми, проходящими по линиям упрочнения AB и DE петли упругопластического гистерезиса (УПГ). Поэтому A j можно представить как сумму трех сил, две из которых есть предельные значения ДВС 1-го и 2-го полуциклов ДД: R u ⁽¹ j ⁾ ( t ₁ ), R u ⁽² j ⁾ ( t ₃ ), а третья включает квазилинейную силу c ⁽ j ¹⁾ ( t ₂ ), действующую в j -м этаже к моменту начала разгрузки, равную:

• ^е У\ t 2 ) = tgP ₅Уj                        ⁽⁸⁾

Тогда величина A j , учитывая соотношение в (4) R t 1 ) = A , y о , , равна

• A , = А У о + abs ( R U 2) ( 1 3 )) + tg P, у p) ,          (9)

где t 3 – время начала нелинейной работы (повторная текучесть) в сечениях стоек j -го этажа (соответствует точке D на ДД).

Второе слагаемое в (9) записывается по абсолютной величине, так как R u ⁽ j ²⁾ ( t ₃ ) < 0. Последнее слагаемое c ⁽ j ¹⁾ ( t ₂ ) численно равно ординате между параллельными прямыми, проходящими через точки О и С под углом р j (рис. 3). В физическом смысле это слагаемое суть величина упрочнения материала, приобретенного стойками j -го этажа за 1-й полуцикл ДД.

Присвоим величине A j верхний индекс, который в отличие от других величин будет означать номер соответствующей петли упругопластического гистерезиса ДД. Величину A ⁽¹ j ⁾ будем называть амплитудой предельных ДВС 1-й петли УПГ ДД (или короче: предельной амплитудой 1-й петли).

Кроме того, будем придерживаться следующего правила. Так как каждая петля УПГ содержит два полуцикла ДД: предыдущий и последующий, то номер петли УПГ будем определять по номеру предыдущего полуцикла в петле.

Участок нагружения CD . На данном участке ДВС имеет вид:

R ⁽ j ²⁾ ( t ) = R e ⁽ j ²⁾ ( t ) = R e ⁽ j ¹⁾ ( t ) – R ⁽ p ¹ j ⁾ ( t 2 ) =

= tg a , [ y j ⁽ t )^- у Pj ) ],                             ⁽10)

где R _e ⁽ _j ²⁾ ( t ) – квазилинейная составляющая ДВС 2-го полуцикла ДД выражается через соответствующие величины (5), (6) 1-го полуцикла.

Участок упрочнения DE . На этом участке ДВС получаем по формуле:

R ⁽ j ²⁾ ( t ) = R ⁽ j ¹⁾ ( t ) – A ⁽ u ¹ j ⁾

как разность между ДВС R(j1) (t), определяемой в (4), и предельной амплитудой A(1j) . Учитывая (3) и (7), имеем

R j ²⁾( t ) = j t ) + (1 - ^ 1 ) А У о, =

= tg P j -у/ t ) + (1 - ^ i ) A y о ,                 (11)

Используя аналогию с ДВС на участке AB в 1-м полуцикле, выразим вектор R ⁽ j ²⁾ ( t ) через сумму квазилинейной и предельной составляющих ДВС:

R j ²⁾( t ) = R eP ( t ) + R u n t 3 ).

Первое слагаемое R e ⁽ j ²⁾ ( t ) получим с помощью вспомогательного построения – прямой Cm || Oq (рис. 3), вычитая из силы R_e ⁽¹ j ⁾ ( t ) в (4) величину (8):

R e ( t ) = R e ( t ) - j ( t 2 ) = tg , у ( t ) - у W ].

Для определения предельной ДВС 2-го полуцикла R u ⁽ j ²⁾ ( t ₃ ) приравняем выражения (7) и (9), откуда будем иметь

R , ( 1 3 ) = (1 - ^ 1 ) A y 0 + tg P j-y j

Очевидно, что сумма R ep( t ) + R up( 1 ₃) совпадает с результатом (11).

Участок разгрузки EF . Этот участок диаграммы характеризуется наличием необратимых деформаций отрицательного знака, приобретенных в результате повторной разгрузки в стойках j -го этажа в момент времени t ₄ (см. точка E на рис. 3). Так как суммарные пластические перемещения этажа равны ( y ⁽ _p ¹ _j ⁾ – y ⁽ _p ² _j ⁾ ), то остаточная составляющая восстанавливающей силы определяется выражением R (j ) ( 1 ₄ ) = tg a , ■ ( у ( j - у p ) ). Тогда ДВС на участке EF можно получить вычитанием величины R ⁽ p ² j ⁾ ( t ₄ ) из квазилинейной составляющей 1-го полуцикла R , ( t ) = tg a , ^у ,, ( t ):

R ⁽ j ²⁾ ( t ) = R e ⁽¹ j ⁾ ( t ) – R ⁽ p ² j ⁾ ( t 4 ) =

= tg a , ^[ y j ⁽ t )^-( у Р У^- у ( j ^{) )]}.                   ⁽¹²⁾

Общий случай для m полуциклов

Полученные результаты (10)–(12) можно распространить на общий случай физически нелинейных колебаний с произвольным числом полуциклов.

Участки нагружения ( OA, CD, … ). На данных участках восстанавливающая сила содержит квазилинейную и остаточную составляющие:

R jm ) ( t ) = R ej ( t ) - R j ^{- 1)} ( 1 2 m -2 ) = = tg ^a j ^{[ у} j ⁽ t )^- b jm ^{- 1) ]},

R® ( t ) = tg ^a j ■ у,- , R pm ^{- 1)} ( 1 2 m -2 ) = tg a , b⁽ m ^{- 1)} .

Участки упрочнения ( AB, DE, .. .). На этих участках ДВС включает квазилинейную и предельную составляющие (рис. 4):

R jm ) ( t ) = R . ( t ) + R m ) ( t 2 m 1 ) — c ^{- 1)} ( t 2 m —2 ) = = R ej ( t ) ⁺ a j m ) ( t 2 m -1 ) = ^tg P j y ( t ) ⁺ a j m ) ( t 2 m -1 ) ,

^ (14)

R j ( t ) = t’l- ( t ) ,

a j m ) ⁽ t 2 m -1 ) = ^R jm ) ⁽ t 2 m -1 ) ^- c (jm 1) ⁽ t 2 m -2 ) •

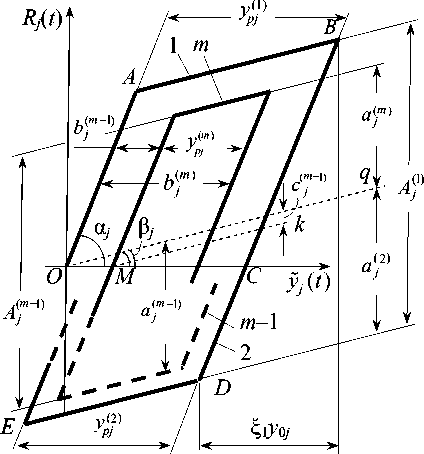
Рис. 4. Диаграмма деформирования с m-м полуциклом цикла. Для удобства записи выражения a(jm) (t2m–1) введен коэффициент ^0 = 1.

Предельная амплитуда m -й петли УПГ равна

A j^m ) =abs ( a j ) ( 1 2 m— 1 )- a ( j m ^{+ 1)} ( 1 2 m+ 1 )) = A y ^ ^ m .

На любом квазилинейном интервале времени t e [ t i , t_i+1 ] можно выделить следующие особенности построения зависимостей (13–15). Из трёх составляющих ДВС только квазилинейная сила является функцией времени, причём на каждом участке m -го полуцикла данная составляющая выражается через характеристики 1-го полуцикла ДД. Две другие составляющие ДВС (предельная и остаточная) на любом участке m -го полуцикла являются постоянными величинами, не зависящими от времени. Такое представление ДВС позволяет, не прибегая к локальным системам координат, выполнять временной анализ в единой системе координат, общей для всех состояний расчетной модели, независимо от характера протекающих в конструктивных элементах процессов (нагружение, упрочнение, разгрузка).

Матричная форма записи

Полученные формулы можно использовать для построения моделей упругопластических колебаний при условии, что нелинейные процессы протекают одновременно в нескольких этажах каркаса. В общем случае вектор ДВС и его составляющие на квазилинейном интервале времени t e [ t_i , t_i+1 ] записывается так:

Участки разгрузки (BC, EF, …). ДВС имеют вид:

R j^m ) ( t ) = R j ( t ) - R ( p m ) ( 1 2 m ) =

= tg ^a j ^[ y j ( t ) ^- b^j m ) ] ,

^ (15)

R(t) = Re(t) + Ru(ti) – Rp(ti),(16)

Re (t ) = KiY (t),

Ru (ti) = Ru (ti-1 ) + AK(ti)Yo, [

R p ( t i ) = R p ( t i -1 ) + K ( t i ) Y pj ( t i ) ,

R ej ( t ) = tg a j y ( t ) , ^R p m ^{) (} t 2 m ) = tg a j b^{j m} ) .

В формулах (13), (15) величина b ⁽ j^{s )} =

= ^ ( -1)* ' y pk ) ( s = m -1, m ) выражает суммарное k =1

пластическое перемещение стоек j-го этажа на момент времени t2s, соответствующий s полуциклам ДД. В (14) величины ajm), cjm-1) имеют вид m-1

a Г ( t2 m-1) = A jy0 j ^ ( -1) ^k, k=0

Cjm-1) (12m-2) = bjm-1)tgPj, где a(jm) представляет обобщенную предельную восстанавливающую силу m-го полуцикла. Согласно (14), эта сила согласована с уровнем 1-го полуцикла (посредством прямой Oq, рис. 4) и численно равна ординате, заключенной между прямой Oq и касательной к линии упрочнения m-го полу- где Re(t), Ru(ti), Rp(ti) – векторы квазилинейних, предельных и остаточных составляющих ДВС; Ki = [rkl(ti)] (k, l = 1, … , n) – матрица жесткости квазиупругой системы; AKi = Ki-1 - Ki - разность матриц жесткости на i–1-х и i-х интервалах времени; Y0 = [y0j], Ypj(ti) = [ y(pkj)(ti)] (j = 1, … , n) – векторы, соответственно, предельно упругих и остаточных перемещений стоек j-х этажей каркаса.

Элементы rkl(ti) матрицы жесткости каркаса зависят от жесткостей стоек j-х этажей, за величины которых в зависимости от состояния системы к моменту времени ti отвечают параметры tgaj или tgPj на ДД (см. рис. 2, 3). Вектор Ypj(ti) остаточных перемещений j-го этажа каркаса формируется в момент начала разгрузки и имеет следующую структуру: первые j–1 компоненты вектора равны нулю, остальные, начиная с j-й, равны перемещению y(pkj) , где k – номер полуцикла ДД. Векторы предельных Ru(ti–1) и остаточных Rp(ti–1) ДВС фор- мируются на предыдущем интервале времени t G [ ti-1, ti ].

Разделение вектора ДВС (16) на линейную составляющую R_e ( t ), зависящую от времени, и постоянные составляющие R_u ( t_i ), R_p ( t_i ) даёт возможность построения алгоритма решения нелинейной динамической задачи. В соответствии с алгоритмом весь процесс нелинейной реакции во времени разбивается на ряд последовательных квазилинейных интервалов t g [ t i , t i +1 ] ( i = 0, 1, ...), внутри которых динамическая реакция вычисляется по схеме упругого решения.

Для реализации такой задачи подставим вектор ДВС (16) в ОДУ (1а). Перенося постоянные составляющие ДВС в правую часть уравнения, формируем на интервале t g [ t i , t i ₊₁ ] вектор обобщённой динамической нагрузки

f ( t ) = P ( t ) – R u ( t i ) + R p ( t i ).                        (18)

В левой части уравнения движения находится линейная составляющая ДВС (17) R_e ( t ) = K_iY ( t ), обеспечивающая выполнение предложенного алгоритма. В результате такого преобразования приходим на квазилинейном интервале времени t g [ t i , t i ₊₁ ] к анализу линейного дифференциального уравнения (19а) при начальных условиях (19б):

M + C i Y ( t ) + KY ( t ) = f ( t ) , (а) Y ( t_z ) = Y o , Y ^ ( t i ) = Y o.      ( б )

Непрерывность процесса колебаний квази-упругой расчетной модели обеспечивается постановкой начальных условий (19б), назначаемых из аналитических выражений реакции в конце предыдущего интервала времени t g [ t i _—1 , t i ].

Выводы

Предложена математическая модель колебаний многоэтажного каркаса с упругопластической восстанавливающей силой, аппроксимируемой кусочно-линейно функцией в координатах «восстанавливающая сила – относительное перемещение». Выражения ДВС получены для произвольного номера полуцикла диаграммы жесткости и представлены в виде суммы линейной и нелинейной составляющих. Показано, что линейная составляющая ДВС для любого участка диаграммы всегда строится для 1-го полуцикла ДД независимо от числа петель упругопластического гистере- зиса и независимо от характера участка в пределах полуцикла. Это позволяет выполнять временной анализ в рамках единого алгоритма для всех состояний расчетной модели (при нагружении, упрочнении и разгрузке).