Построение математической модели формирования радиотелефонного канала для передачи аудиоинформации

Согласно концепции устойчивого развития сельских территорий России на период до 2020 г., опубликованной Центром экономической безопасности Российской Федерации [1, с. 30], необходимо обеспечить телефонизацию всех сельских населенных пунктов и объектов социальной сферы. Однако прокладка проводных линий связи невозможна в силу действующих экономических или технических ограничений [2]. Задачи телефонизации в таких условиях могут быть решены с помощью систем расширения проводных линий связи, одним из вариантов решения может быть радиоудлинитель телефонной линии. Устройство включает в себя абонентский и базовый блоки, которые находятся на значительном удалении друг от друга. Устройство работает следующим образом. Абонент поднимает трубку стандартного телефонного аппарата, подключенного к абонентскому блоку, и, услышав предварительную готовность, осуществляет выбор линии, далее базовый блок подключает выбранную телефонную линию, и устройство разрешает набор номера в обычном режиме. При входящем вызове со стороны базового блока происходит сканирование линий связи, и при получении звонка происходит пересылка данных о номере линии, с которой пришел вызов на сторону абонента. Информация о выборе линии пересылается с помощью двухтональных многочастоных сигналов набора номера (DTMF) пониженной частоты, чтобы исключить несанкционированное использование канала устройства. Устройства формируют канал связи между собой посредством стандартных выпускаемых промышленностью радиостанций [2]. Необходимо построить математическую модель устройства для того, чтобы получить представление о процессах, происходящих при передаче аналоговой информации в радиоудлинителе, посредством математического описания. Математическая модель устройства была заявлена на международной заочной конференции «Технические науки: традиции и инновации» [3], где были приведены тезисы, касающиеся ее структуры. Ниже приводится полное математическое описание и обоснование модели, вывод формул и конкретизация параметров.

Цель моделирования радиоудлинителя состоит в теоретическом изучении процесса установления связи между блоками и передачи аудиоинформации при заданных условиях внешней среды, а также внутренних служебных процессов коммутации внутри блоков системы. Необходимо установить математические и аналитические зависимости между параметрами аудиоинформации, приближенно описывающими поведение системы.

Данная модель актуальна в связи с необходимостью показать общую структуру детерминированных сигналов, передача которых является непосредственной задачей ра-

Рис. 1. Структура моделируемой системы

диоудлинителя, принцип действия которого заключается в перенесении свойств удаленной телефонной линии к телефонному аппарату абонента посредством дуплексного радиоканала [2]. Модель позволит спрогнозировать прямые и косвенные последствия реализации заданных способов воздействия на объект с учетом изменений отдельных параметров полезного сигнала и ограничивающих факторов передачи.

Для построения модели рассмотрим, как исследуемый объект взаимодействует с внешней средой. Объект имеет свойство непрерывно усложняться, поэтому будем считать его сложной системой различных компонент, взаимосвязанных друг с другом. Таким образом, имеет место системный подход к созданию модели, при котором необходимо выделить систему S и внешнюю среду E [5, с. 21]. При этом модель также является системой S’ = S’(M) , рассматриваемой относительно внешней среды E [5, с.22]. Структура системы приведена на рис. 1 .

На основании данных о внешней среде построим модель и выявим ограничения для построения системы [5, с. 24].

Влияние модели внешней среды E’ носит ограничивающий характер в виде рекомендуемых параметров элементов передачи данных, достаточных для функционирования системы в целях решения поставленных в публикации [2] задач. Расчетные данные внешней среды приводятся ниже. Модель адекватна объекту при условии соответствия исчисленных параметров моделируемой системы реальному объекту. Таким образом, в данном случае, кроме математического, имеет место также натурное моделирование, то есть проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия [5, с. 36], являющейся основанием теории моделирования [5, с.31].

Перейдем от описания объекта к непосредственному составлению модели. Элемент аналоговой коммутации предназначен для формирования аудиоканала связи [2], что указывает на колебательный характер процессов, происходящих в последнем. Сказанное верно и для элемента аутентификации с той разницей, что аутентификация производится с помощью двухтональных многоча-стоных сигналов (DTMF) [2]. Очевидно, что элементы ау-

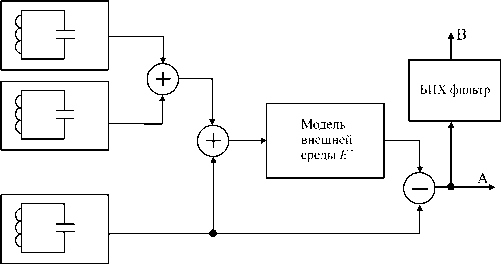
Рис. 2. Функциональная схема модели аналоговых процессов описываемой системы тентификации и аналоговой коммутации в общем случае представляют собой источники колебаний, в пределах модели для них могут быть определены сходные функции, поэтому в качестве основы для количественной и качественной описательной оценки происходящих в устройстве процессов, то есть в качестве модели устройства подходит колебательный LC-контур [4, с. 50]. Cоставим функциональную схему математической модели. ункциональная схема модели аналоговых процессов системы приведена на рис. 2.

Уравнение, описывающее колебательный процесс в одном из простейших электрических колебательных контуров [4, с. 50], изображенных на рис. 2 , следующее (1):

L^q = -Cq, (1)

где L – значение индуктивности контура; d²q/dt² – дифференциал по времени функции, описывающей значения заряда конденсатора; С – значение емкости контура, q – величина заряда, прикладываемого к обкладкам конденсатора.

Произведем преобразование выражения (1) к виду, допускающему анализ процессов изменения величины напряжения u(t) , а также составим уравнения, описывающие поведение сложного сигнала, модулирующую последовательность и уравнение модулированного сигнала.

По определению dq i =        [4, с.50], dt следовательно, из уравнения (1) получим (2):

qt - ) C = L d " •                                      (2)

dt

Так как по физическому смыслу величины C , в любой момент времени допустимо равенство u(t) = q(t)C , то перепишем (2) в виде (3):

di u (t) = L — . dt

Уравнение (3) справедливо для каждого из электрических колебательных контуров модели, приведенной на рис. 2 , однако каждый из колебательных контуров имеет собственную частоту колебаний, поэтому переменные равенств (3), кроме времени t, различны для каждого из них, поэтому справедливы равенства (4), (5), (6):

di ui-0 = Li T ’ dt di 2

u 2( t) = L 2     , dt di uз(t) = L3 "T ' dt

Равенства (4), (5), (6) справедливы соответственно для каждого из трех колебательных контуров, изображенных на рис. 2 сверху вниз.

Для математического моделирования сложного сигнала в системе, состоящего из нескольких частот, необходимо сложить сигналы, выраженные равенствами (4) и (5), таким образом, получим равенство (7):

u - ( t ) - L - di- + u - ( t ) - L₂ di ² = 0.

^{1        1} dt ^{2        2} dt

Сгруппируем переменные выражения (7), следующим образом (8):

u_x-t ) + u ₂( t ) - ( L dt + L ₂ -^) = 0.                (8)

Для дальнейших преобразований в модели в уравнении (8) обозначим u ..(0 = U1 (t) + u2(t) и L0CH^ = Ldi- + L.di2.

ocн dt 1 dt 2 dt

Получим уравнение основного для данной модели сложного сигнала, который для передачи через модель внешней среды необходимо промодулировать. Уравнение (9) выглядит следующим образом:

u   ( - ) = L   di oc-- •                                       (9)

ocн         ocн dt

Уравнение (9) представляет в модели сложный аналоговый сигнал, который должен быть промодулирован. Выражение (10) для амплитудно-модулированного сигнала следу- ющее [6, с. 136]:

u am ( t ) = u - ( t ) [ ^{1 + mS} ( t ) ] ,

где u_am (t) – промодулированный сигнал; u_c (t) – несущее колебание; S(t) – информационный сигнал; m – коэффициент модуляции, m = const .

Промодулируем сложный основной сигнал, описанный в выражении (9), подставив переменным в выражения (10) выражения (9) и (6), таким образом, получим следующее уравнение для модулированного сигнала (11):

u-m(t) = L3 dT 1 + mLocH dOH- • dt L

Для детектирования сигнала нужно преобразовать уравнение (11) к уравнению (12) следующим образом [5]:

di di di u (t- = L- —- + L- —- mL ----.(12)

am          3           3           осн dt dt dt

Кроме того, необходимо учесть соотношение сигнал-шум [6, с. 175] по формуле (13):

С/Ш = Р/2ηW ,                              (13)

где С/Ш – соотношение сигнал-шум; Р – мощность сигнала, ηW – коэффициент, учитывающий амплитуду шумов и ширину полосы частот.

Для данной модели учитываем, что приемо-передающий элемент, изображенный на рис. 2 , генерирует только гауссовы шумы с амплитудой η/2 .

Мощность сигнала является ограничением, накладываемым внешней средой, и имеет квадратичную зависимость от расстояния [7, с. 178]. Запишем выражение для мощности передаваемого сигнала (14):

_{P =}

^P г ^D n p ^D n ^{λ 2} 4 π ² S ²

где P – суммарная мощность сигнала; Рг – мощность передатчика в момент приема абонентом сигналов, для данной модели примем Рг = const; Dnp, Dn – коэффициенты, опре- деляющие усиление сигнала в направлении к приемнику и от него, для целей данной модели примем равными единице, считаем Dnp Dn = const; λ – длина волны, аналогично вышесказанному, λ = const; S – расстояние между приемо-передающими элементами среды E, изображенными на рис. 2, поскольку расстояние между приемо-передающими подсистемамиобъектавреальностинеизменяется,тосчитаем S = const.

Подставляя выражение для мощности передаваемого сигнала (14) в выражение (13) получаем уравнение (15) для определения соотношения сигнал-шум модели внешней среды E’ :

C / Ш = ^{г np n} .                              (15)

8 π ² S ² η W

БИХ фильтр, или фильтр с бесконечной импульсной характеристикой, в данной модели предназначен для имитации устройств, ответственных за распознавание двухтональных многочастотных сигналов набора номера, и работает по алгоритму Герцеля, подробно описанному в публикации [8].

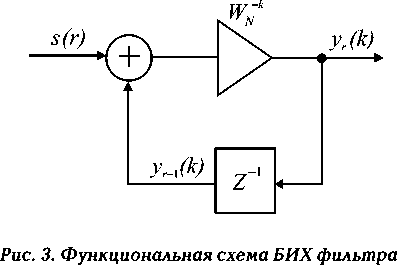
Опишем математически фильтр с бесконечной импульсной характеристикой, показанный на рис. 4 . Изображенный на рисунке БИХ фильтр работает по алгоритму Герцеля. Для вывода уравнений, описывающих математически процессы, происходящие в данном элементе, необходимо, прежде всего, опереться на уравнение БИХ фильтра первого порядка. Функциональная схема БИХ фильтра спектрального отсчета с номером k приведена на рис. 3 .

Выведем уравнение для БИХ фильтра, изображенного на рис. 3 , используя публикацию [8]. Покажем также передаточную характеристику фильтра. Запишем выражение (16) для дискретного N -точечного преобразования Фурье значений сигнала s(n) при n ∈ (0…N – 1) :

N - 1

5 ( k ) = ^ s(n) x IP ^k ,                          (16)

n = 0

где S(k) – комплексные отсчеты спектра по Фурье; s(n) – значения отсчетов сигнала; W N ^{x k} — поворотные коэффициенты, обладающие следующим свойством:

2 п

W v k ^X N = ^exP( — j — x n x k ) - при ^{k G (0}^^{N -} 1) .

Умножив выражение (16) на W - ^{k x N} , получим выражение (17):

N - 1

5(k ) = W - ^{k x} N X £ 5 ( n ) x W n ^{x k} .                 (17)

n = 0

Раскрыв сумму, выделяя спектральные отсчеты с вынесением W _N ^{k x N} за скобки, как показано в публикации [7], получаем рекуррентное выражение (18) для вычисления спектрального отсчета k на N – 1 шаге вычисления:

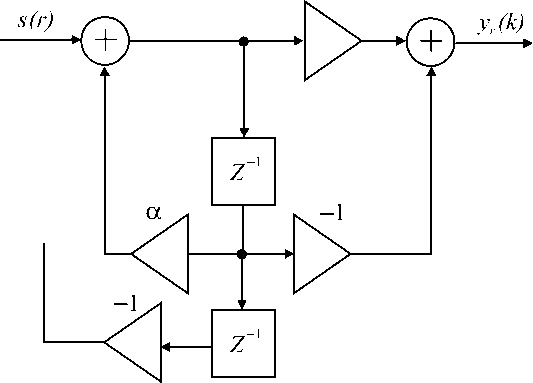
Рис. 4. Cтруктурная схема БИХ фильтра Герцеля

Умножив выражение (19) на 1 — W-^k X z ¹ с учетом

W-k + Wk = 2Xcos(N xk) [12], получим передаточную характеристику более сложного БИХ фильтра, работающего в соответствии с алгоритмом Герцеля и позволяющего вычислить спектральный отсчет k с меньшей затратой ресурсов, чем фильтр на рис. 4. Значение (20) вещественного коэффициента α для схемы на рис. 4 [8]:

a = 2 x cos(2 x nx N).

Для схемы, изображенной на рис. 4 , значение S(k) определяется уравнением (21):

5(k) = WN k x v(N -1) - v(N - 2).

В уравнении (21) промежуточные значения v(N – 1) и v(N – 2) рассчитываются итерационно по формуле (22):

v(r) = 5 (r) + 2 x a x v(r -1) - v(r - 2).

Поворотные коэффициенты уравнения (21) имеют реальную часть

S(к ) = у, (к ) = W - *' N X ( s ( r ) + у, _ , ( к )),           <¹⁸>

k

W N ^k R = cos(2 x n x — ) ^и мнимую

где s(r) – отсчет входного сигнала с номером r .

Данное рекуррентное выражение на шаге с номером r = N – 1 позволяет нам получить спектральный отсчет номером k [8]. Выражение (18) представляет собой разностное уравнение фильтра с бесконечной импульсной характеристикой (БИХ фильтра), структурная схема которого приведена на рис. 4 . В выражении (18) обозначим через X(z) и Y(z) элементы s(r) и y_r(k) , получим передаточную характеристику (19) H(z) БИХ фильтра, показанного на рис. 3 :

k

W N ^k R = sin( 2 x n x — ) части

С учетом последних исчисляются реальная –

S R — V ( N — 1) X W ^- k r — V ( N — 2) и мнимая —

S _t = V ( N - 1) x W n ^k I части спектральных отсчетов.

H ( z ) =

Y ( z ) =     W_N^k

X ( z )   1 - W N ^k x z -¹'

Таким образом, алгоритм Герцеля сводится к итерационному расчету v(r) по формуле (22), где последние итерационные значения помещаются формулу (21) для окончательного

пересчета спектрального отсчета S(k) . Очевидно, что реальные и мнимые части поворотного коэффициента уравнения (21), а также коэффициент α уравнения (22) опираются на характер сигнала. Конкретизируем форму колебательного сигнала для электромагнитного колебательного процесса, описанного в уравнениях (4) – (12).

Электромагнитные колебания в идеальном колебательном контуре, изображенном на рис. 2 , подчиняются гармоническому закону. Уравнение (23), описывающее процесс изменения величины u(t) , выглядит следующим образом:

u ( t ) = U m COS( to t + ф ), (23)

где u(t) – функция изменения величины напряжения; U_m – максимальное (амплитудное) значение u(t) ; ω – угловая частота, ω = 2πf или ω= 2π /Т ; ϕ – сдвиг фаз.

С учетом (23) сложный колебательный процесс, описанный уравнениями (7) и (8), может быть представлен уравнением (24) следующим образом:

U i ⁽ t ) + u 2 ⁽ t ) = U rn 1 c ^os( ® 1 t ⁺ P i ) ⁺ U m 2 co ^s( ® 2 t ⁺ P 2 ^). (24)

имеем системы аналогичных уравнений для сигнала с аналогичной системой ограничений.

Система уравнений (28), описывающая характеристики колебательного сигнала модели во времени, выглядит следующим образом:

^U OCH ⁽ t ) = u 1⁽ t ) ⁺ u 2⁽ t ),

L   diocн ocн dt

= L di¹- + L ₂ di ², dt dt

и UA = L ocн          ocн

d io c н dt ’

>

Выполним преобразование, аналогичное (9), получим (25):

u осн ⁽ t ) = ^U moc COS( to oсн t + ф осн ).                      (25)

По формуле (10) промодулируем сигнал, описанный уравнением (25), получим (26):

u am ⁽ t ) = Urn ! ^C °s( ® 3 t ⁺ Ф 3 ) [ 1 ⁺ m ^U m oc„ ^CO s( ® o_m t ⁺ Ф осн ) ] • ⁽²⁶⁾

Выше было замечено, что влияние модели внешней среды E’ носит ограничивающий характер.

Приведем ограничение (27) распространения сигнала, выведенное по формулам (14) и (15), обозначив максимальное значение полезного сигнала, как U_m , паразитного – как U_n .

^{P г D np D n λ 2 U n Um ≥} 8 π ² S ² η W

.

Отношение полезного сигнала к значению шумов должно быть достаточно велико [6, с. 178]. Выражения di

1 + mL .   / > 0, dt

1 + mU_mo ch cos( ^нt + Ф_ос J >  0 mocн         ocн      ocн

истинны при выполнении условий

L

ocн

di ocн dt

< 1

U cos( to t + ф ) < 1 и ⁰< m ^ 1

mocн         ocн      ocн

иначе возникнет перемодуляция сигнала, то есть избыточная модуляция, демодуляция такого сигнала приведет к его искажениям [6, с. 136].

Коэффициент α для уравнения (22) должен изменяться по закону (20), также при моделировании по алгоритму Герце-ля нужно учесть мнимые и реальные части. Таким образом,

u am ^{( 1} ) = ^L 3 di r ^{1 +} m ^L dt

di ocн ocн dt

•

Приведем систему ограничений для системы уравнений (28). Ограничения вызваны присутствием материальных объектов, составляющих внешнюю среду E системы, непосредственно не входящих в модель [4, с. 99]. Соответствующая системе уравнений (28) система ограничений (29) выглядит следующим образом:

l di=c

L c dt <¹ di ■ ^{1 + m}L.„^ >  0, ■ 0 <  m <  1.

Для конкретизации описания формы колебательного сигнала LC-контура модели приведем следующую систему уравнений (30), описывающих гармоническую составляющую сигнала:

^UOCH ( t ) = u 1 ⁽ t ) ⁺ u 2 ⁽ t X

^UmocH ^COS( ® ocH t ⁺ Ф осн ^X = ^Um 1 ^C0S( ® 1 t ⁺ Ф 1 ) ^{+ U}m 2 ^C0S( ® 2 t ⁺ Ф 2 ^X

Uoch (tX = UmocH COS(®ocHt + Фосн X uam (tX = Um 3 C0S(® 3 t + Фз) [1 + mUmocH COs(®ocHt + Фocн )]•

И30)

Соответствующая ей система ограничений (31) выглядит следующим образом:

Umoсн cos(^,ct + ^>c J < 1, mocн         ocнocн

1 + mU   cos(to t + ф ) > 0, m o cн         o c н   ϕ o c н,

< 0 <  m <  1,

PD D X2U

U > г np nn_

_ ^m     8n²5²nW

Приведем систему уравнений (32) для описания подсистемы, моделирующей обработку сигнала на принимающей стороне:

v ( r ) = 5 ( r ) + 2 x a x v ( r - 1) - v ( r - 2), 5 ( k ) = W_N ^k x v ( N - 1) - v ( N - 2).

Система ограничивающих условий (33) для данной системы следующая:

a = 2 x cos(2 x n x N ),

W n ^k R = cos(2 x n x N ),

• - W N ^k I = sin(2 x n x N ),

S r = v ( N - 1) x W N ^k r - v ( N - 2), S I = v ( N - 1) x W _N ^k I .

При построении математической модели установлены законы получения и распространения детерминированных сигналов, уравнения (28) – (31), при взаимодействии подсистем системы передачи информации радиоудлинителя телефонной линии [2], влияния внешней среды при уточнении способов управления формирования и передачи сигналов при заданных условиях внешней среды. При подготовке данной публикации было составлено математическое описание колебательных процессов передачи аналоговых сигналов через систему уравнений (28), которое конкретизировано через описание формы сигнала системами гармонических уравнений (30). Также составлена система ограничений (29) и (31) в зависимости от внешней среды; составлена система уравнений (32) с системой условий (33), описывающие процесс детектирования сигнала при аутентификации устройства. Приведенная математическая модель приближенно описывает процессы передачи информации для устройства интеллектуального радиоудлинителя телефонной линии [2]. Модель адекватна реализации полезной модели радиоудлинителя телефонной линии [2] с некоторой степенью приближения, что позволяет оценить параметры передаваемых сложных сигналов по времени и по форме и вычислить их при различных начальных условиях. Модель позволяет вести расчет по параметрам передаваемых сигналов, дает возможность рассчитывать показатели по комплексным отсчетам спектра сигнала при анализе, прогнозировать прямые и косвенные последствия реализации заданных способов воздействия на объект с учетом изменений отдельных параметров полезного сигнала и ограничивающих факторов передачи.

В настоящее время на радиоудлинитель телефонной линии имеется патент [9]