Построение математической модели экстрагирования подсырной сывороткой из люпина в форме пластины

Предпосылками для построения модели послужило следующее:

• 1.    Исследование кинетики процесса извлечения экстрактивных веществ из частиц люпина в форме сферы, цилиндра и пластины показало предпочтительность последней формы: выход целевого компонента был выше [3]. Это обусловило выбор формы частицы для математического описания процесса экстрагирования.

• 2.    Люпин как материал растительного происхождения с клеточной структурой считаем изотропным, то есть с однородной структурой и одинаковой диффузионной проводимостью во всех направлениях. При этом d <<  l , где d - размер клетки; l - определяющий размер тела.

Сформулируем задачу. Частица люпина рассматривается как неограниченная пластина, поскольку её ширина b и длина l существенно превышают толщину 5 : Ь/ 5 = 5; l] 5 = 10. В этом случае неограниченная пластина представляет собой тело, ограниченное двумя параллельными плоскостями, и в ней устанавливается одномерный диффузионный поток в направлении минимального размера.

Общая площадь поверхности частицы F-шй — 2F1 + 2F2 + 2F3, где F1, F2 — площади торцевых поверхностей по длине и ширине;

F ₃ — площадь боковой поверхности. В этом случае

(2F + 2F2 )/(2F + 2F2 + 2F3) — 0,23, а отношение 5 /1 — 0,1. С учётом изложенного размерность области решения задачи может быть по- нижена.

Итак, в одномерной постановке задачи дифференциальное уравнение молекулярной диффузии запишется в виде [7]

⁹ С — D 9 2 C , (1) 9 т       9 х ²

где C - текущая концентрация диффундирующего вещества в порах, кг/м³; т — время, с; D - коэффициент диффузии, м²/с; х — координата, м.

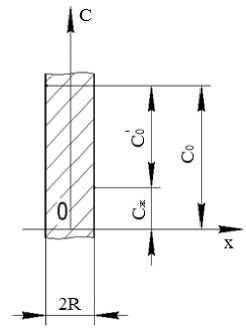
Рисунок 1. К концентрации окружающей среды и плоской неограниченной пластины (при т = 0; задано С_о = const и С _о'— const )

Дадим пояснения к рисунку 1: С _о, С^ -концентрация в порах в начальный момент времени и концентрация окружающей среды, кг/м³; 2 R — толщина пластины, м.

Запишем значения начального С _о' и текущего C ' концентрационных напоров (кг/м³): C ₀' = С ₀ — С ж ; C ' = С — С ж . Тогда безразмерная избыточная концентрация 0 — C '/ C '₀.

Сформулируем допущения. В начальный момент ( т = 0) концентрация в пластине распределена равномерно и равна С = С_о — const . Концентрация окружающей среды постоянна

C^ = const. На обеих поверхностях отвод экс- трактивных веществ осуществляется при постоянном во времени коэффициенте массоотдачи в = const. Отсчет концентрации пластины для любого момента времени проводится от концентрации окружающей среды. Изменение концентрации происходит только по координате Ох.

Тогда уравнение (1) запишется иначе:

9 С' _    9 ² С'

.

9т      9хх

Формулировка начальных условий при ( т = 0) очевидна:

C ' = С -0 = С 0 — С ж ; ц ( x ,0) = ^ 0 ,    (3)

где ц - вязкость жидкости в капилляре, Паю;

ц -химический потенциал, соответствующий концентрации C0.

При заданных условиях процесса экстрагирования задача становится симметричной и начало координат целесообразно поместить на оси пластины (рисунок 1).

Не вызывает сомнения постановка граничных условий на оси и на поверхности пластины, которые записываются в виде:

х = 0; I      I = 0 ,

V 9х ) х=0

х = R ; I — I — — ^в C_R .       (4)

х — R

V ⁹ х J х — R     2 m

Первое условие характеризует отсутствие концентрационного потока, второе -массоотдачу с поверхности.

В уравнениях (4): в — коэффициент мас- соотдачи, м/с; 2 — коэффициент массо-проводности, м2/с.

Уравнение (2) в совокупности с краевыми условиями (3) и (4) однозначно формулируют задачу: найти распределение концентрации по толщине пластины в любой момент времени.

Приведем решение задачи поставленной задачи. Решение дифференциального уравнения (2) ищем в виде произведения двух функций, из которых одна выписана как функция т , а другая - как о , то есть: C ' — C '( т , х ) — ^ ( т ) • ^ ( х ) [1].

Подстановка и разделение переменных позволяют записать:

^ (т ) + Dk ^(т ) — 0; V ( x ) + к ²щ{ x ) — 0, где ^ ( т ), v ( x ) — переменные; к — постоянные.

После интегрирования частные решения запишутся в виде:

^ ( т ) — Сe ^D ' ^{к т} ; v ( х ) — С ₂ sin( kx ) + C ₃ cos( kx ).

Тогда общее решение уравнения (2) принимает вид: C ' ( x , т ) = [ C ₂ sin( kx ) + C cos( kx ) ] • C_xe~ D ' ^k 2 ^T (5)

Распределение концентрации является симметричным относительно оси ординат, следовательно, должно описываться чётной функцией f ( x ) = f ( - x ). Такой функцией является cos( kx ) , а sin( kx ) есть нечётная функция x и поэтому исключается из решения [5].

Уравнение (5) удовлетворяет исходному (2) при любых значениях постоянных C 1 , С 2 , С 3 и k .

В результате решения характеристи-

Запишем конечное выражение для поля концентраций при экстрагировании из плоской пластины:

n ^ro

0= 2

2 sin ц

(Цп + Sin Цп cosЦп )

Уравнение (8) даёт возможность получить значение концентрации в любой точке пластины для любого момента времени.

Проведем анализ полученного решения . Поскольку μ 1 , μ 2 , ..., μ n представляет собой ряд возрастающих чисел, то чем больше

ческого уравнения

ц ^ц = и

где ц = kR с

учётом граничных условий (4) получим систему уравнений, в которой каждому найденному значению корня μ , будет соответствовать своё

частное распределение концентрации:

/      X    2 D T

I х I - ^ц

C \ = A cos ц — e R ;

^{1     1} I ¹ R J

μ , тем меньше роль последующего члена ряда по сравнению с предыдущим. В то же время, чем больше число Fo , тем члены ряда будут убывать быстрее с увеличением номера n .

Большим числом исследований [2, 4, 6] показано, что уже при Fo_m >  0,3 ряд становится настолько быстросходящимся, что распределение концентрации достаточно точно опи-

C\ = A co

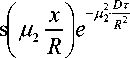
сывается     первым     членом     ряда:

2sin ц                   ₇

0 =  -----:----------- cos ( Ц X ) exp( - Ц Fom )• (9)

( Ц + sin ц cos ц )     ^{1         1}

Обозначим

_D =      2sin Ц 1

¹   ( ц + sin ц cos ц )

.

/       X    2 D T

I      X I - ^Ц п 12

C= A coS ц — e R nn   n k R J

.

Частные решения (6) будут удовлетво- рять дифференциальному уравнению при любых значениях постоянных A1, A2, ..., An, одна- ко ни одно из этих решений не будет соответствовать действительному распределению концентрации в начальный момент времени. Поэтому путем наложения бесконечного числа таких распределений при соответствующем выборе величин An представляется возможным воспроизвести любую действительную концентрационную зависимость в начальный момент времени. С учётом изложенного общее решение выражается суммой бесконечного ряда всех частных решений:

ro

C ' = 2 A n co n = 0

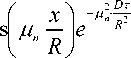
Применяя разложение частной функции в ряд Фурье и опуская промежуточные рассуждения, из начальных условий (3) определяются выражения для постоянной A :

A n = C'

2sin ц _п

( p _n + sin Ц п cos Ц п )

Видно, что A является только функцией корней характеристического уравнения, которые, в свою очередь, являются функцией массообменного критерия Био.

Величина D является только функцией числа Bi и заранее может быть рассчитана и табулирована. Кроме того, если рассматривать концентрацию для определенных значений безразмерной координаты, например, для оси и поверхности пластины ( Х = 0 и Х = 1, соответственно), то второй множитель уравнения (9) тоже зависит только от числа Bi . Тогда решение имеет вид:

⁰ X = 0 = N ^{( B}i m ) ^еХР^{( -} Д 1^{2 Fo} m ) ;        ⁽¹⁰⁾

⁰ X = 1 = ^{P ( B}i m ) exP^{( -} A ^{2 F}o m ) •         ⁽¹¹⁾

Функции N(Bim) и P(Bim) заранее рас- считаны и представлены в справочниках в виде таблиц в зависимости от числа Bi , а безразмерные избыточные концентрации для оси и поверхности пластины могут быть построены в виде номограмм. С этой целью следует прологарифмировать уравнения (10) и (11), тогда они будут представлять собой семейство прямых линий:

ln 0X=0 = ln N(Bim ) - Ц12Fom ), ln 0X=1 = ln P(Bim ) - Ц12Fom ).     (13)

Как следует из (9), для любого момента времени при заданных граничных условиях поле концентрации имеет вид симметричной кривой с максимумом на оси пластины (Х=0). Для каждого последующего момента времени будет своя кривая, монотонно убывающая к поверхности пластины. При этом касательные к кривым в точках поверхности (X = ±1) проходят через две направляющие точки +А и –А, расположенные на расстоянии ±Хо от поверхности пластины, X0 = 1/Bim .

Проведём доказательство этого важного свойства, для чего рассмотрим поле концентраций для произвольного момента времени Fo_m >  0. Умножив граничное условие (4) на R/C '„ при x=±R , получим:

Тогда решение задачи будет иметь вид:

п ^ю

0= X

- п =1

( — 1) ^{п + 1}

(2 п — 1)

— cos t (2 п — 1)~ X

■ exp

2 п — 1 1 2

I - Fo„

2 J        ^m

а уравнение с концентрацией экстрактивных веществ на оси пластины ( Х=0 ) примет вид:

4 п ^м (_ IV⁺¹ 0х-о= - S ⁽ 1) exp X =0 л Й (2и-1) ^F

—

2 п — 1 Y 2_F

I ^{- FO}m

.

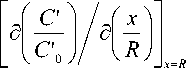
— ( CL I Я С' I

^ m V C 0 J x = R

При Х= 1 0 х=/ = 0, поскольку:

cos (2 п — 1)- X

\      2

= 0.

В безразмерных переменных имеем:

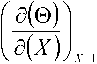
— Bi 0

m

X = 1 .

Тогда:

Ранее было отмечено, что при Fo_m >  0,3 ряд (9) быстро сходится и ошибка не превышает 1 %, если отбросить все члены ряда, кроме первого. При этих условиях уравнение (16)

—

X = 1

0 X = 1

X 0

= tg v ,

^X 0 = 1Л . (14)

Bi m

Таким образом, касательные ко всем концентрационным кривым в точке пересечения с поверхностью пластины и при неизменных граничных условиях всегда будут проходить через точку А . Тогда возможно определить характер изменения концентрации в теле при заданном значении массообменного числа Bi .

Рассмотрим случай, когда Bi стремится к бесконечности. Тогда концентрация поверхности пластины теоретически сразу становится равной концентрации окружающей среды, в которую помещена пластина. Это следует из уравнения (14): при Bi , стремящемся к бесконечности, X_o = 1/ Bi_m = 0 . Следовательно, точка

пересечения касательных к концентрационным

кривым находится на поверхности пластины. Из Bi _m = ( R/ A m )/( 1/ в ) следует: Bi_m стремится к бесконечности при заданных физических параметрах и толщине пластины тогда, когда в

стремится к бесконечности, то есть когда организована высокая интенсивность отвода экстрактивных веществ от поверхности. В нашем случае эффект достигается с помощью низкочастотных механических колебаний и тогда процесс экстрагирования определяется физическими свойствами и размерами частиц люпина. При этом ^_n=(2n—1)( — /2), а коэффициент ряда описывается уравнением (9):

_{D =}      2 sin ц        4( — 1) ^{п +1}

^п    ц _п + sin ц _п cos ц _п    - (2 п — 1)

можно переписать так:

⁰ X = 0 = -exp -

—

- 1

Fo

2 J     m

После логарифмирования уравнения (17) и решения его относительно числа Фурье,

имеем:

Fo m

4 , ( 4   1

= ^ln ”X— ^-   V ^{- 0} X = 0

Конечное время экстрагирования т , то

есть продолжительность процесса, получаем, учитывая, что Fo_m = Dr/R² :

т

к

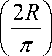
1ln

Г 4   1

V ^{- 0} X = 0

Покажем, что модель адекватна экспе-

риментальным данным. СВ,%

25 -

20-

15-

10-

60 Т.мин

Рисунок 2. Зависимость извлечения экстрактивных веществ из люпина подсырной сывороткой от времени при параметрах механических колебаний: частота колебаний 50 Гц, амплитуда 10 мм, t = 50 оС, форма частицы люпина - пластина, – расчёт.

Из рисунка 2 видно, что полученные решения уравнений модели находятся в хорошем согласии с экспериментальными данными.

Вестник ВГУИТ, №1, 2015