Построение математической модели преобразователя ультразвукового сигнала с целью практической реализации микропроцессорной системы сканирования высокотемпературных изделий

Выбор преобразователя сигнала для любой системы сбора и обработки информации имеет большое значение, особенно в случае ультразвукового неразрушающего контроля, когда преобразователь является одним из основных компонентов системы.

Особое внимание при выборе преобразователя следует уделить условиям контроля, в первую очередь свойствам материала и условиям контакта преобразователя с объектом контроля [1].

Не менее важным является и выбор конфигурации преобразователя, когда выбирают между фокусирующими преобразователями и преобразователями со сменными защитными насадками, защищающими рабочую поверхность, или рассматривают различные разновидности этих преобразователей. При этом важно, чтобы преобразователь имел требуемую частоту, соответствовал измеряемому материалу и имел правильный размер активного элемента.

Особую сложность вызывает ультразвуковое сканирование высокотемпературных изделий, поскольку с повышением температуры в исследуемом объекте происходит искажение распространения звуковых волн. Разрушение преобразователя имеет место и при контакте с поверхностью, нагретой более 50 ° С [2].

В качестве примера построения модели излучателя рассмотрим ультразвуковое исследование нагретого до 300 ° С стального образца (сталь 4340), имеющего толщину до 200 мм.

В общем случае под ультразвуком понимают излучение на частоте выше 20 кГц, однако при ультразвуковом исследовании используют диапазон от 100 кГц до 50 мГц. Частоту излучения определяют как

f = р CD где f – частота; Т – период незатухающей волны.

Скорость распространения звука в полностью упругом материале при одной температуре и давлении постоянна:

X = с, X = cT, (2)

где X - длина волны; с - скорость звука в материале; f – частота; Т – период.

Для определения частоты излучателя воспользуемся табличными данными (табл. 1). Однако изначально сле- дует определить характер излучаемой волны (продольная или поперечная). При ультразвуковом исследовании используются и продольные, и поперечные волны, а также в специальных случаях – поверхностные (релеевские) и плоские волны (волны Лэмба).

Чем меньше длина волны, тем больше на нее влияет среда распространения, и поэтому при анализе материалов используется максимально допустимая для данного материала частота.

Известно [3], что при применении для ультразвукового исследования поперечной волны чувствительность к мелким дефектам повышается, а затухание с расстоянием увеличивается, следовательно в случае измерения толщины требуется применение излучателя продольной волны, который менее чувствителен к мелким дефектам и имеет меньший коэффициент затухания.

Таким образом, используя соотношения (1) и (2) и рассматривая единичную волну (приняв X = 1), для исследования стали 4340 получаем частоту излучателя продольной волны порядка 5…6 мГц.

При проведении ультразвукового исследования измеряются две величины: время пролета (время прохождения ультразвуковой волны через материал) и амплитуда принятого сигнала. Эти параметры определены следующим соотношением:

Т = f •

где Т – толщина материала; с – скорость звука в материале; t – время пролета. Используя это соотношение, рассчитаем время пролета для стального бруска толщиной 200 мм. Оно составит 0,001 с.

Для измерения плотности материала по величине затухания или для выявления дефектов используют данные об относительном изменении амплитуды сигнала, которое выражают в децибелах и определяют логарифмичес- ки исходя из соотношения двух сигналов:

dB = 20log₁₀

f A ) —L

l A 2 J

где dB – децибелы; А ₁ – амплитуда первого сигнала;

А ₂ – амплитуда второго сигнала.

Примеры коэффициента ослабления сигнала для раз-A личных соотношений 1 приведены в табл. 2.

A ₂

Основываясь на вышеизложенном, с целью уточнения результатов сделаем дополнительные расчеты частоты используемого излучателя.

При проведении ультразвукового сканирования получена следующая форма волны (рис. 1) [4].

Форма волны датчика и спектральный анализ выполняются в соответствии с определениями и условиями проведения теста ASTM E1065. Обычно для частотного анализа в качестве единиц измерения используются мегагерцы, для анализа формы волны – микросекунды и для определения пика амплитуды – децибелы [1].

Рассмотрим пик частоты прохождения ультразвука в исследуемом материале. С увеличением частоты амплитуда выходного сигнала растет. Здесь следует обратить внимание на верхний и нижний пределы частоты. При достижении нижнего предела коэффициент ослабления становится равным 2, т. е. мы имеем 6-децибеловый сигнал (рис. 2). При достижении верхнего предела коэффициент начинает монотонно падать. Таким образом, нас интересует только этот 6-децибеловый диапазон.

Известно соотношение между мегагерцевой полосой пропускания и длительностью прохождения волны (рис. 3) [1]. В этом соотношении разброс на –40дБ больше, так как 1%-й задний конец формы волны содержит очень небольшое количество звуковой энергии и поэтому оказывает очень малое влияние на анализ полосы пропускания. Из-за рассеивания это наиболее подходящий вариант для точного определения формы волны за промежуток времени, мкс, и спектров в частотной области.

Таблица 1

Акустические свойства материалов [1]

Материал	Скорость продольной волны, м/сек	Скорость поперечной волны, м/сек	Акустический импеданс, кг/(м2 с ⋅ еск)∙1088)
Алюминий	6 320	3 130	17,06
Бериллий	12 900	8 880	23,5
Латунь морская	4 430	2 120	37,30
Кадмий	2 780	1 500	24.02
Ниобий	4 920	2 100	42,16
Медь	4 660	2 260	41,61
Золото	3 240	1 200	62,60
Инконел (жаропрочный и жаростойкий сплав на никелевой основе)	5 820	3 020	49,47
Железо	5 900	3 230	45.43
Чугун (с малой скоростью)	3 500	2 200	25,00
Чугун (с высокой скоростью)	5 600	3 220	40,00
Свинец	2 160	700	24,49
Молибден	6 250	3 350	63,75
Никель чистый	5 630	2 960	49.99
Платина	3 960	1 670	84,74
Серебро	3 600	1 590	37,76
Сталь 1020	5 890	3 240	45,63
Сталь 4340	5 850	3 240	45,63
Сталь   марки   302   аустенитная нержавеющая	5 660	3 120	45,45
Сталь 347 аустенитная	5 740	3 090	45,40
Жесть	3 320	1 670	24,20
Титан марки Ti 150A	6 100	3 120	27,69
Вольфрам	5 180	2 870	99,72
Цинк	4 170	2 410	29,61

Таблица 2

Коэффициенты ослабления сигнала

А A 1,1,%%//А А 2, %	Коэффициент	dB
100 70,71	1,414 2	3
100 50	2	6
100 25	4	12
100 10	10	20
100 1	100	40

Основываясь на данных рис. 3, можно определить частоту датчика.

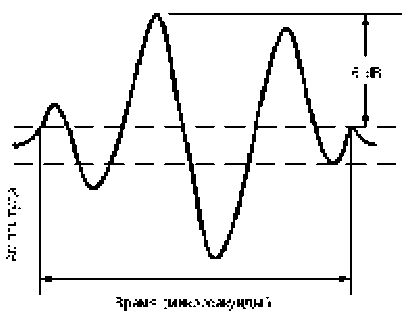
Рис. 1. Волна на уровне 6 дБ (50%-й пик амплитуды)

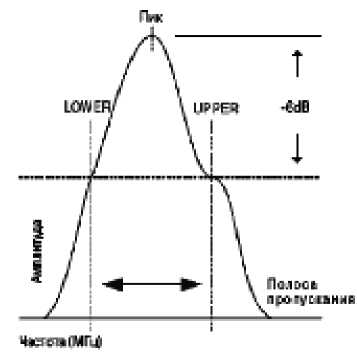
Рис. 2. Пик частоты прохождения для исследуемого материала

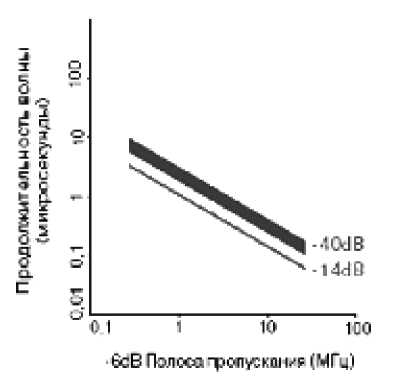
Рис. 3. Длина волны и полоса пропускания

Если, например, требуется – 14-децибеловая волна за 1 мкс, то какой следует выбрать датчик? На графике (см. рис. 3) полоса пропускания от 1 до 1,2 МГц соотносится примерно с 1 мкс – 14-децибеловой протяженности длины волны. Принимая номинальный 50%-й фракционный широкополосный датчик, получаем среднюю номинальную частоту от 2 до 2,4 МГц. Поэтому может быть использован датчик частотой 2,25 МГц или 3,5 МГц.

Не менее важны исследования акустического импеданса материала, который является показателем противодействия смещению его частиц звуком:

Z = P c,

где Z - акустический импеданс; P - плотность материа- ла; с – скорость звука в материале.

Граница между двумя материалами с разным акустическим импедансом называется акустической границей . При нормальном падении звука в акустическую границу часть звуковой энергии отражается, а другая часть продолжает свое перемещение в материале. Потеря энергии, дБ, при прохождении сигнала из среды 1 в среду 2 рассчитывается следующим образом:

( dBloss = 1010g1ol 7-1-2-2 I ,

V ( Z 1 + Z 2 ) )

где Z ₁ – акустический импеданс первого материала; Z ₂ – акустический импеданс второго материала.

Необходимо учесть потерю энергии децибелового сигнала в среде 1 при отражении от акустической границы со средой 2:

(            2)

dB loss = 10log io | (_¹    _²) I .                (7)

v ⁽ Z 1 + Z 2 ) )

Например, потеря сигнала при его распространении из воды ( Z = 1,48) в сталь 1020 ( Z = 45,41) составит –9,13 дБ. Потеря децибелового отраженного эхо-сигнала в стали 1020 составит –0,57 дБ, что также соответствует потере эхо-сигнала при распространении в обратном направлении. При Z ₂ >  Z ₁ происходит переворот формы волны.

В материале происходит увеличение затухания ультразвука. При отсутствии значительных отражателей вы- деляют три варианта затухания:

– преломление;

– рассеивание;

– поглощение.

Характеристики затухания ультразвука в материале имеют важное значение при выборе датчика ультразвукового контроля. Для выявления этих характеристик рассмотрим звуковое поле, чувствительность и фокусную зону датчика.

Звуковое поле датчика (рис. 4) описывается следующими зависимостями:

N = Df,                (8)

4 C

N = D 2 ,                   (9)

4X где N – протяженность ближнего поля; D – диаметр элемента; f – частота; с – скорость звука в материале; X - длина волны.

Чувствительность датчика определяется диаметром звукового луча в интересующей точке:

1, 02 Fc

= fD ’

BD = 0,256 8 DS F ,              (11)

где BD – диаметр луча; F – фокусное расстояние; с – скорость звука в материале; f – частота, D – диаметр элемента; S_F – нормированное фокусное расстояние.

Для определения фокусной зоны датчика (рис. 5) рассмотрим начальную и конечную точки, которые расположены в точке падения амплитуды сигнала «импульс – эхо» до –6-децибеловой амплитуды в точке фокуса (рис. 6). Длина фокусной зоны вычисляется по формуле

F = NS^ f ( 2 + 0,5 S f ) , (12)

где F – фокусная зона; N – ближнее поле; S_F – нормированное фокусное расстояние.

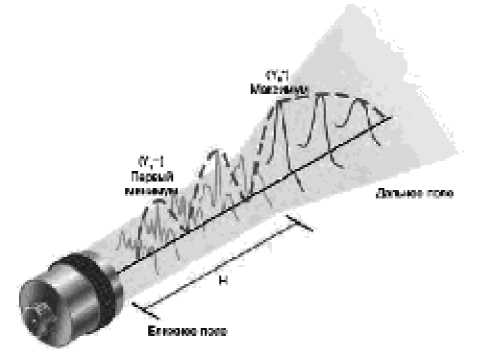
Рис. 4. Звуковое поле датчика

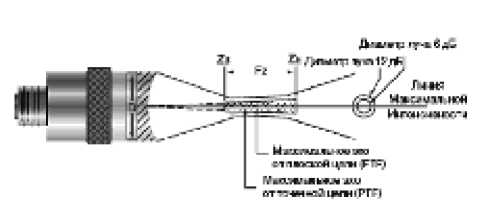
Рис. 5. Фокусная зона датчика: Z_В – начало фокусной зоны;

F_Z – фокусная зона; Z_E – конец фокусной зоны; D – диаметр элемента

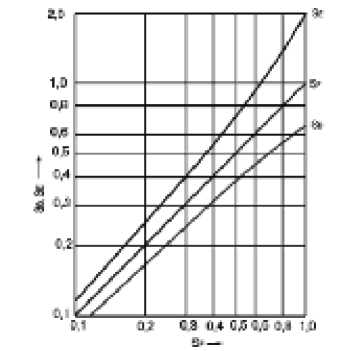
Рис. 6. Конечная и начальная точки фокусной зоны –6 дБ при измерении амплитуды сигнала

Все звуковые волны рассеиваются, и это характерно для любого датчика. В ближнем поле звуковой луч имеет сложную форму, а в дальнем он рассеивается (рис. 7).

Угол распространения луча плоского датчика –6-де-цибелового импульса рассчитывается следующим образом:

sin |a| = 0,514 —,              (13)

12 J fD где a / 2 - половина угла рассеивания луча между точка ми –6 дБ.

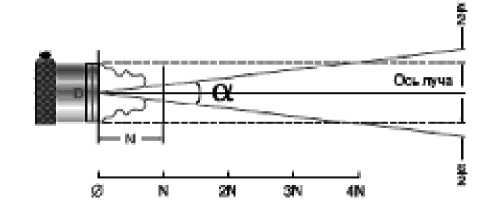
Рис. 7. Рассеивание луча и половинный угол

Таким образом, угол рассеивания луча можно варьировать, изменяя частоту и диаметр датчика, на чем основана работа датчиков ультразвукового контроля.

Различают раздельные, совмещенные и раздельно-совмещенные датчики. В последнем случае на одной конструкции размещают вмонтированные в отдельные линии задержки передающий и принимающий элементы, которые детектируют основной импульс достаточно просто. А если линии задержки расположены под углом, то информация о фокусном расстоянии такого датчика достаточна для определения проникающей способности звукового луча. Поэтому раздельно-совмещенные датчики нашли более широкое применение при исследовании неоднородных материалов.

Таким образом, математическая модель преобразователя ультразвукового сигнала адекватно описывается выражениями (1)…(12).

При ультразвуковом сканировании высокотемпературных изделий, в частности бруска стали, нагретого до 200.. .600 ° С, согласно приведенным выше расчетам, целесообразно применять ультразвуковой датчик с рабочей частотой порядка 5 MГц и диаметром 25 мм. Кроме того, необходима дальнейшая разработка методики проведения исследований и реализация экспериментального образца микропроцессорной системы на основе высокопроизводительного сигнального процессора DSP.