Построение минимизирующих последовательностей в системах с неограниченными управлениями

Многие прикладные задачи оптимального управления являются вырожденными [1 – 10], так что известные общие методы оптимального управления и классические вариационные методы для них оказываются неэффективными, либо вообще неприменимыми.

Типичный класс вырожденных задач представляют задачи c линейными неограниченными управлениями:

I (u() x(•)) = F(x(tF )) ^ inf, T = [t,, tF ],(0.1)

x(t) = g(x(t), t) + (h(x(t), t), u(t)V x(tI) = xI, x(t) e R", u(t) e R,(0.2)

x(t) е X(t).(0.3)

В отличие от классических задач, где предполагается существование оптимального решения, доставляющего минимум функционала, здесь под решением задачи понимают мини мизирующую последовательность { u s ( • ), x s ( • ) } , на которой I ( u s ( • ), x s ( • ) ) ^ inf I ( u ( • ), x ( • ) )

при s ^^. Управление us (•) будем считать кусочно-непрерывным, траекторию xs (•) - непрерывной кусочно-дифференцируемой функцией. Такие последовательности представляются посредством обобщенных решений типа импульсных режимов управления.

Во многих работах по оптимальному импульсному управлению при исследовании задач вида (0.1) – (0.3) постулировалось выполнение условия коммутативности (корректности):

—        д h д hp h --- h дx 4

– коммутатор (скобка Ли) гладких

[hp,hq] = 0, p,q = 1,k , где [hp,hq] = ^qhp дx функций hp,hq , и (hl)x – матрица Якоби.

В статьях [11 – 13] показано, что условие Фробениуса не является необходимым условием для метода преобразований и позволяет преобразовать исходную систему к производной системе, менее сложной, чем его выполнение в системах того же порядка.

В работе [13] предложен подход к построению траекторий импульсных режимов управляемых систем, основанный на представлении предельной системы как управляемой с неограниченными линейными управлениями и ее последовательном преобразовании к эквивалентным системам понижающегося порядка, называемых производными системами.

Цель исследования состоит в том, чтобы, опираясь на известный метод преобразования к производной задаче [4, 6, 7] и предложенную в [13] схему построения траекторий предельной системы на ее орбите, разработать процедуру построения минимизирующей последовательности в общем случае, без упомянутого предположения о корректности и с учетом возникающих при этом особенностей .

1. Преобразование к производной системе , орбита предельной системы

В работах В.И. Гурмана [4, 6, 7] предложен метод преобразования вырожденных задач к производным задачам с переходом к производной системе меньшего, чем n , порядка так, что траектория x E ( • ) ( E означает «extension» - расширение), фигурирующая в производной системе в роли управления, аппроксимируется по мере последовательностью { x s ( • ) } допустимых траекторий исходной системы.

Производная система, безотносительно какой-либо оптимизационной задаче, имеет вид: y ⁽ t ) = ( % ^, g ^{( x (} t ^), t )) + П ^, y = n ⁽ t ^, x ^),                         (1. ²⁾

где y = n(t, x) — m -мерное интегральное многообразие (m < n) предельной системы, которая строится следующим образом. Система (0.2) представляется в виде x^) = g(x^)IIt) + Еhj(x(т),t)u^, t(T) = ТТ^, t(0) = 0, те[0,TF],    (L3)

и(т)||      н j            ||u(т)||             ||u(т)|| где т - вспомогательный аргумент. При достаточно больших управляющих воздействиях в системе (1.3) ее динамика главным образом определяется слагаемыми в правой части уравнений, зависящими от управления. В пределе при ||и|| ^ ^ она переходит в систему, называемую предельной:

k

5 & ( т ) = £ h p ( x( т ), t ) l^p , || l || = 1 , т е [0, T f ] , t = const .                  (1.4)

p = 1

Правая часть системы (1.4) задает линейную оболочку размерности к . Функция n i (t , x ) будет называться первым интегралом системы (1.4), если на любой траектории x( т ) этой системы она постоянна, т.е. n i ( t , x ( т )) = const , где i <  к . Совокупность независимых первых интегралов системы (1.4) - интегральный базис: y = n ( t , x ) •

Были сформулированы достаточные условия, обеспечивающие указанное преобразование, основное – полная управляемость системы (1.4) на интегральном многообразии y = n ( t , x ) [4, 6, 7].

Понятие орбиты [14] напомним в терминах алгебры Ли семейства векторов h ₁ , …. h_k . Пусть Lie ( h ₁, ..., h_k ) – алгебра Ли, генерируемая добавлением к семейству h ₁ , …. h_k всех скобок Ли [ h i , h j ] , [[ h i , h j ], h l ] , .„ ( i , j , l = 1, к ) и их линейных комбинаций. Пусть L ( x ) -линейная оболочка алгебры Lie ( h 1 , ..., h_k ) в точке x е E" . Если dim L ( x ) = m <  n , то предельная система вполне управляема на некотором связном m -мерном многообразии O с R" - орбите семейства h 1 , .^. h_k :

O y = { ^{( x ):} y = П ⁽ t ^{, x} ) } ^{,                                  (1} .5)

где t является параметром. Размерность орбиты равна размерности линейной оболочки ал40

гебры Ли. Конечно, явно выписать уравнение орбиты системы (1.5) в общем случае невозможно, тогда необходимо неявное описание [7].

В производной системе функции y ( t ) – играют роль кусочно-гладких фазовых траекторий, а функции x ( t ) – роль кусочно-непрерывных управлений, связанных с фазовыми координатами конечными соотношениями (1.5) так, что разрывы происходят вдоль траекторий предельной системы, соединяющих левый и правый пределы в точке разрыва. Таким образом, в некоторый момент t возникает задача построения траектории предельной системы (1.4), соединяющей некоторые точки

x (0) = x 0 , x ( T f ) = x _T ,                                (1.6)

F удовлетворяющей уравнению орбиты (1.5). Вектор y определяется начальным условием.

В общем случае решение такой задачи для управляемой системы неединственно, и эту неединственность можно использовать для построения наиболее простых траекторий, что важно для их последующей аппроксимации допустимыми решениями исходной системы при построении минимизирующей последовательности.

Пример 1. Рассматривается система

1     1         1    2     212

x = g (x) + u , x = g (x) + xu , x3 = g3(x) + (x1)2u2/2, x4 = g4(x)-2xxu 1, te T = [0, 1], xl 4(0) = 0'

и задача оптимального управления с целевым критерием

I (u (•), x (■) ) = ( x 1(1)) + x 4(1) ^ inf,(1.8)

при дополнительном поточечном фазовом ограничении - 1 <  x 1 ( t ) <  1 , t е T .

Системе (1.7) соответствует предельная система:

x'(t) = 11, x2(t) = x1(т)12, x3(t) = (x*)212/2, x4(т) = -2xх(т)11, те [0,TF],(1.9)

в которой не выполнено условие коммутативности:

h1( x) = (1,0,0, -2 x1)T, h2 = (0, x ',( x T/2,0)T, h3 = [ h1, h 2] = ^ h,-^ h 2 = (0,1, x 1,0)T ^ 0. dxd

По первому и четвертому уравнениям системы (1.9) находится их первый интеграл:

dx ⁴ = - 2 x ¹ dx ¹ , n ( x ) = ( x 1 ) 2 + x ⁴ = const .

который, как легко убедиться, задает орбиту системы:

n _x 1 h .+ П 2 h 2 + n _x з h 3 = 0 , O y = { ( x ): y = ( x 1 )² + x ⁴ } .

Перейдем в системе (1.7) к новым переменным x ^{1 - 3} и y = ( x 1 )² + x ⁴ :

5&^х( т ) = 1 ³, x ²( т ) = x¹1 ², x\ f ) = ( x ³) ² 1 2/2 , у( т ) = 0 , т е [0, т ] .          (1.10)

F

Имеем у0 = (x0)2 + x4. Предельная система не вполне управляемая в R4, но вполне управляемая на связном 3-мерном многообразии Oy , проходящем через начальную точку x 4 (0) = x0-4. Положим g(x) = (1,0,0,0)T . Производная система (1.2) имеет вид:

у ( t ) = 2 x 1 ( t ) , у (0) = 0 .                                (1.11)

Система (1.11) - первого порядка, в ней шесть переменных: у , x ^w, u ¹². Все переменные, кроме y , являются управляющими и могут быть заданы произвольно как кусочнонепрерывные функции x^{1 -} , й^х_Е² , определяющие некоторый импульсный режим. Критерий оптимальности (1.8) с учетом уравнения орбиты O_y представляется в виде

I = у (1) ^ inf .                                 (1.12)

Имеем регулярную задачу оптимального управления, решение которой XVE (t) = -1. Тогда у(t, XVE ) = -21, XЕ(t) = -21 -1, t e T. Функции 5cE 4(t) не удовлетворяют начальным ус- ловиям. Этим функциям при t е (0,1] отвечает управление uE (t) = -1, но для иллюстрации возможности решения задачи при произвольном выборе функций xiE3, й^"1 полагаем u',' = 0 на всем отрезке T. Таким образом, имеем x1E (t) = -1, xE 3( t) = 0, x4( t) = -2t -1, y (t, xE ) = -2t, йЕ-2 = 0 на T, min У (1) = -2. Нужно построить последовательность {xs (■)} для приближения траектории xЕ (■) по мере на отрезке T. □

2. Управляемость предельной системы на орбите

Краевые условия означают требование перевода системы (1.4) из заданного начального состояния x в фиксированное конечное состояние x . Рассмотрим, как перейти из на-0F чального состояния в конечное по траектории системы (1.4), лежащей на орбите.

Для исследования системы (1.4) перейдем к вспомогательной системе k д^т) = ^hp(x(т),t)up(т), те [0,тF], t = const.                  (2.1)

p = i

В соответствии со схемой, предложенной в [13], система (2.1), линейная по неограниченным управлениям, представляется в виде mr

5с( т ) = h ( x , t ) u + h ( x , t ) й = ^ h i ( x , t ) u i + ^ h j ( x , t ) u^j , те [0, т _F ] , t = const , i = r + 1                    j = 1

где при управлениях u i = 0 получаем корректную систему (это заведомо верно, если число управлений u j равно 1). Находится ( n - r )-мерный интеграл у = n ( x , t ) корректной системы и рассматривается система, производная по отношению к (2.1):

у ( т ) = n _xh ( x , t ) u , y = т / ( x , t ) , n _xh(x , t ) = 0 , t = const .

Переменные производной системы можно назвать «активными», а остальные – «пассивными». Множество «активных» переменных обозначим как NonPas , «пассивных» – Pas .

Тем самым вводится множество E_x кусочно-непрерывных функций x ( т ) , таких что функции у( т ) = т / ( x ( т )) кусочно-гладкие и удовлетворяют производной системе.

Для системы вида (2.1) существует преобразование ( x ) ( у , z ) , где z = f ( x ) - вектор криволинейных координат на интегральном многообразии. Обратное преобразование x = £ ( у , z ) . Исходная система (2.1) преобразуется к системе

у ( т ) = n _xh ( x , t ) u , у = т / ( x , t ) , nJPx , t ) = 0 , t = const , Z ( т ) = ^ _x ( h^z ( x , t ) u + hi(x , t ) й ) , x = ^ ( у , z ) .

По аналогии с системой (1.7) может оказаться, что уравнения системы изначально разделены на «активные» и «пассивные». Изучим этот случай подробно. Для получения производной системы достаточно записать систему без «пассивных» уравнений. Получим расширенную предельную систему:

•x j ( т ) = ^ h^J_p ( x ( т ), t ) v^p ( т ), т е [0, т _F ] , t = const , j е NonPas .            (2.2)

p

«Управляющие» функции x i ( т ) ( i е Pas ) могут быть разрывными, в том числе на концах отрезка [0, т _F ] . Функции x^j ( т ) ( j е NonPas ) будем строить непрерывными и удовлетворяющими соответствующим краевым условиям из (1.6). Управления u 1 ( т ) , —, u^k ( т ) и x i ( т ) ( i е Pas ) в системе (2.2) надо задать таким образом, чтобы вычислялись решения x j ( т ) ( j е NonPas ), удовлетворяющие орбите. Рассмотрим функции u 1 ( т ) , —, u^k ( т ) постоянными на всем отрезке [0, т _F ] , а функции x i ( т ) ( i е Pas ) - постоянными на интервале ( т₁ , т _F ) и принимающими на концах отрезка значения, равные граничным состояниям:

xTI ’ T = /,, ur(т) = z2r, r e 1,k,   x1 (т) = ■ xi, T e (Ti, Tf ), ^ xTF = F, i e Pas.

(2.3)

Заметим, что в расширенную систему (2.2) могут быть подставлены вместо определен ных по формуле (2.3) функций x (т) константы xi на [0, TF ], так как в интегральном смысле все равно траектории xj (т) не изменятся. Представление функций x1 (т) в виде (2.3) нужно для выполнения соответствующих номерам i краевых условий из (1.6).

Теперь правая часть системы (2.2) зависит не от неизвестных функций, а от параметров. Система стала проще. Например, если правая часть системы не зависит от x^j , то решение находится непосредственным интегрированием:

Т x j Т) = xj + J £ hrvrdт := xTF .

F k

(2.4)

T I r = 1

В результате решения системы алгебраических уравнений вычисляются управляющие параметры u ¹, ..., u k и x i ( i e Pas ) и, значит, может быть построена траектория x( T ) предельной системы (2.1), удовлетворяющая в каждый момент т орбите, в том числе краевым условиям (1.6). Траектория X ( т ) получается непрерывной по «активным» координатам и разрывной по остальным.

Необходимое условие для выполнения такой процедуры – равенство числа искомых параметров в правой части (2.4) числу уравнений, т.е. числу «пассивных» координат. Если оно не выполняется, то можно идти двумя путями. Первый путь – увеличивать число параметров за счет применения кусочно-постоянных управлений или другого параметрического семейства управлений. Второй путь – уменьшать далее порядок системы путем итеративных переходов к новой производной (относительно предшествующей) системе, что всегда возможно при наличии линейных управлений, которые вместе с новым управлением x e Oy (t, y) задают некоторый пучок гиперплоскостей (в простейшем случае - прямых) [13]. Построив его линейную оболочку, получим систему канонического вида, аналогичную исходной (0.2). При этом базис можно задавать неоднозначно, отправляясь, например, от некоторого поля h1(^(y, Z)), где Z - постоянный вектор криволинейных координат на орбите. При следующем переходе будем иметь семейство производных систем с параметром z , который будет играть роль постоянного по времени управления.

Пример 2. Пусть x1-4 = 1, x1F =-1, x2F = 2, x3F =-1/2, x4F = 1 для предельной систе мы (1.9). Здесь NonPas = {2,3}, Pas = {1,4} , y = 2 . Так как x/ ^ xJF, j = 2,3, полагаем:

	1 x 0 ,	T = T o ;	4 x 0 ,	= 0;
•x'T ) = ■	x 1 = const,	т e (0, T f );        :v 4( T ) = ■	x 4 = y - ( x *)2,	т e (0, T f );
	^ x 1 F ,	T = TF ;	^ x 4 f ,	T = T F .

(2.5)

Определив x^) по формуле (2.3), получаем u^T) = 0 , т e [0, TF ]. По второму и третьему уравнениям системы (1.10) и с учетом краевых условий имеем: ff                               Ff x\тР) = x0 + J x1 u2 de := x2F , x3(TF) = x0 + J 00

-( x *)² u²d e : = x 3 F ,

x¹ й² = a , ( x *)² й²/2 = b , a = ( x 2 F -x 2 ) T , b = ( x 3 F - x 0 ) F F .

Разрешаем систему алгебраических уравнений относительно x ¹ и u ˆ² :

X ¹ = 2 b/a , й¹ = a ² /2 b .                                  (2.6)

Таким образом, для расширенной предельной системы (вида (2.2))

X²( т ) = x '( г ) и ², X³( T ) = ( x *) ² и 2/ 2

функции x '( г ) = X' T ) и й ²( т ) = й²( г ) найдены. Тогда точка ( X 1 , X ⁴) лежит на параболе x ⁴ = у - ( x *)² при данном у . Из точки ( x 0 , x 4 ) попадаем в точку ( X 1 , X ⁴) скачком, затем также скачком переходим в точку ( x T , x T ) , что иллюстрирует рис. 1 при T F = 1 .

FF

Получены непрерывные линейные функции

• ²          2      12                з з 1 ^{2 2}

X ( T )   xT + x й ( Т   v i ) ,   X ( T )   xT  + (x ) й ( т   т i ) I   , удовлетворяющие краевым условиям.

При T F = 1 имеем a = 1 , b = - 3/2 , X ¹ = - 3 , г)² = -1/3 , X ⁴ = - 7 . На рис. 1 показаны графики проекций траектории X( T ) . Пунктирные линии означают разрывы траектории. □

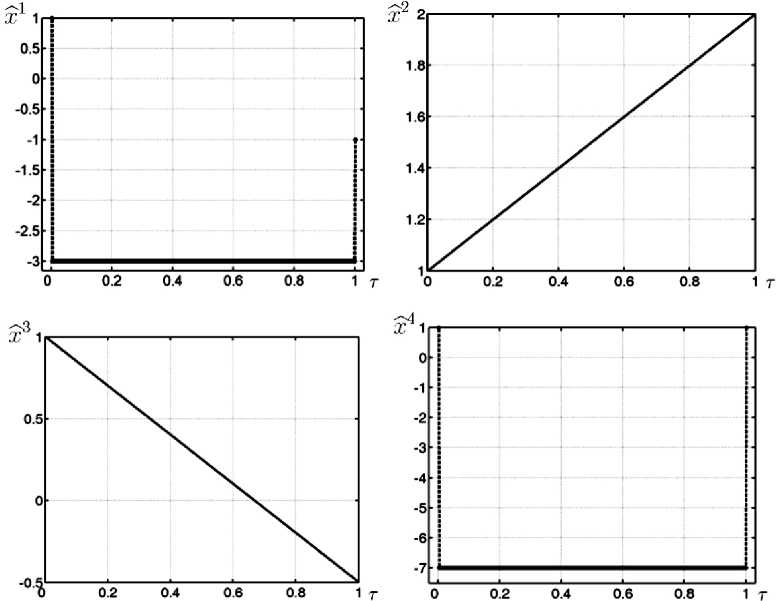
Рис . 1

k

Если оказывается x 0 ₀ = x^J _T ( j е NonPas ), то, например в (2.4) получаем ^ ^й ^r = 0 . Это r = 1

«особый» случай, и формулы для X(T), которые получены ранее в предположении, что xj * xJT (j е NonPas), нельзя применить. Нужно задать каждую константу xi, равной од-F ному из значений x0 или x^F .

• 3.    Аппроксимация траектории предельной системы непрерывными траекториями исходной

Рассматривается система, эквивалентная системе (1.3) при L = || u || и управлениях

V = uj/||u ||, таких, что V е { 0, ± 1 } , || 1 || = 1 , j = 1, к :

r

X & ( T ) = g ( x ( т ), t )/ L + ^ h j ( x( т ), t ) l , t ( T ) = 1 L , t T I ) = t _T I, Te [ T i , T f ] ,        (3.1)

= 1

где L – достаточно большое число.

т

Решая задачу Коши t( т ) = 1[L , т е [0, т _F ], t (0) = 0, находим t ( т ) = j (1/ L ) d e = т/ L , 0

t( т ) = т/L , t т ) = т _F /L , где момент т _F априори не известен.

При L ^ ^ имеем g ( x , t )/ L ^ 0 на [0, т _F ] , но в этом случае значение t( т _F ) ^ 0 .

Схема аппроксимации траектории 5с(т) предельной системы следующая. Задается произвольно достаточно большое значение тF и вводится равномерная сетка на отрезке [0, тF]. Далее система (3.1) интегрируется численно на [0, тF] с управлениями /^{0, ± 1}, и = 1, j = 1, к, и константой L , которые задаются таким образом, чтобы траектория x(f) системы (3.1), исходящая из начального состояния x0, была непрерывной по всем аргументам и в момент тF выполнялось условие xc(тF) = 5c(тF) в смысле критерия error = |jx^) -xF 11 < £.                               (3.2)

На отрезке [0, т _F ] рассматриваются точки т ^ , т 2 , в которых происходит смена значений управлений / 1 , ..., /^к . Эти точки вместе с моментом т _F определяются при достижении «пассивными» и «непассивными» решениями тех или иных значений. Например, если x 0 >  x i ( i е NonPas), то управления будут заданы такими, чтобы на отрезке [0, т 1 * ] функция x i ( т ) убывала до значения x i .

Пример 3. Продолжим исследование, начатое в примерах 1, 2, заменив при этом вектор g ( x ) = (1,0,0,0) T на вектор g ( x ) = (sin x 1 , 1, cos x ², - 1) ^T .

Начальное приближение т _F = 7 . Интегрируем систему (1.7) с управлениями / ¹ =- 1 , / ² = 0 до тех пор, пока функция X ¹( т ) не достигнет значения x¹ с некоторой точностью £ 1 по критерию x ¹ ( т 1 ) - x ¹1 <  £ 1 1 .

Затем на полуотрезке ( т ' , т ²] интегрируем систему (1.7) с управлениями / ¹ = 0 , / ² = - 1 , пока функции x ² , ³( т ) не достигнут постоянных значений x^- F ³ с точностью £ 1 соответственно, тем самым определяя точку т 2 . Далее, на полусегменте ( т : 2 , т _F ] интегрирование системы проводится при / ¹ = 1 , / ² = 0 , пока аппроксимирующая траектория X ( т ) не достигнет заданного конечного состояния с точностью £ по критерию (3.2). На рис. 2 представлены соответствующие графики. □

• 4.    Построение последовательности кусочно - непрерывных функций x_q ( t ) для исходной системы

На отрезке [0, t_F ] вводится сетка

0 = t ₀ <  t 1 = t ₀ + А t <  ... <  tj = j A t <  ... <  q A t = t_F , A t = t_F[q ,          (4.1)

где q – достаточно большое число.

Функции x_q ( t ) выступают в роли «промежуточного звена» при аппроксимации разрывной траектории x ˆ _E ( t ) с помощью непрерывных траекторий x s ( t ) исходной системы, где s – номер члена последовательности, аппроксимирующей x ˆ _E ( t ) по мере.

Укажем свойства функции xq (t) при фиксированном q. На интервалах (tj, tj+1) (j = 0, q) функция xq (t) непрерывная и кусочно-дифференцируемая, является решением исходной системы (0.2) при начальном состоянии xq (tj + 0) е Q(tj, yq (tj)), которое задается из значения xq (tj) = xq (tj - 0) е Q(tj, yq (tj)), где Q(tj, yq (tj)) - орбита предельной системы, порожденная начальным состоянием xq (tj - 0). Функция xq (t) подразумевается непрерывной слева на [t0, t). Запись xq (t0) = xq (t0 - 0) означает xq (t0) = x(t0) = x0. В момент tq = tF предел слева xq (tq - 0) порождает yq (tq), а значение xq (tq), формально равное xq (tq + 0), находится, исходя из орбиты Q(tq, yq (tq)). Точки xq (tj + 0) берутся на орбитах Q(tj, yq(tj)) такими, чтобы величина ||xq (tj + 0) - xE (tj + 0)|| была наименьшей.

Пример 4. Для задачи, поставленной в примере 1, при g ( x ) = (1,0,0,0) T продемонстрируем процесс построения функции x_q ( t ) , положив сначала q = 5 .

В момент 1 ₀ = 0 функция x_q ( t ) принимает заданное значение x_q (0) = 0 . Орбита Q ( 1 0 , y q ( 1 0 )) = { ( x ): y_q ( 1 0 ) = ( x q ( 1 0 ))² + x 4 ( 1 0 ) = 0 } . Значение x_q ( 1 0 + 0) принадлежит аппроксимируемой траектории x E в момент ( 1 ₀ + 0) . На промежутке ( 1 ₀, t 1 ] = (0,0.2] , поставляя управления U E ²( t ) = 0 в исходную систему, находим x q ( t ) = t - 1 , x q ³( t ) = 0 , x ^ (t ) = - 1 . Имеем x q ( t 1 - 0) = - 0.8 , x_q ⁴( t 1 - 0) = - 1 , y_q ( t 1 ) = - 0.36 * ( x^x E ( t 1 ))² + x E ( t 1 ) = - 0.4 , y_q ( t i ) - ( x E ( t i ))² =- 1.36 >  y ( t 1 ) = - 1.4 . В качестве начального состояния для интегрирования исходной системы на следующем частичном промежутке - начиная с ( t 1 + 0) - берем точку ( xq³,y q ( t 1 ) - ( x E ( t 1 + 0))² ) = ( - 1,0,0, - 1.36 ) .

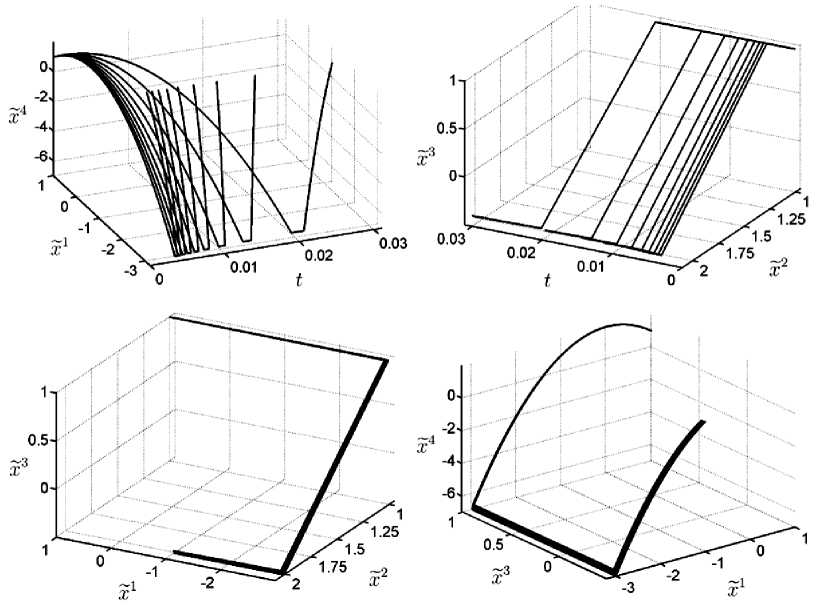
Рис . 2

Далее по аналогии. Получаем x_q ( t_q + 0) = ( - 1,0,0, - 2.8 ) , y_q ( t_q ) - y ( t_q ) = A t = 0.2 . В таблице 1 приведены интересующие нас значения по каждому из пяти промежутков.

Таким образом, xq(t) = t-(1 + jAt), x4(t) = yq(tj)-(.xE(tj + 0))2 при tе (tj,tj+1], j = 0, q -1, и xq’ 3(t) = 0 при t e [t0, t ]. Эти формулы справедливы для любого числа q > 0 . Образуется последовательность {xq (t)} , сходящаяся к xE (t) равномерно на [t0, tq ], причем

I ⁽ ^ q ²⁾ = y q ⁽ t q ) ^ У ⁽ t q ) = ^{тГ 1} ( ^U ) ^ □

Таблица 1

t j	( x E ( t j ), x E ( t j ) )	y ( t j -)	( x ; ( t , + 0), x q ( t , + 0) )	y q ( t j )
0	(-1, -1)	0	(-1, -1)	0
0.2	(—1, -1.4)	-0.4	(-1, -1.36)	-0.36
0.4	(-1, -1.8)	-0.8	(-1, -1.72)	-0.72
0.6	(—1, -2.2)	-1.2	(-1, -2.08)	-1.08
0.8	(-1, -2.6)	-1.6	(-1, -2.44)	-1.44
1	(-1, -3)	-2	(-1, -2.8)	-1.8

• 5.    Построение минимизирующей последовательности { u s ( t ) , x s ( t ) }

Заключительным этапом является построение последовательности кусочнонепрерывных управлений u s ( t ) и непрерывных кусочно-дифференцируемых траекторий x s ( t ) , на которой функционал стремится к инфимуму [6, 7].

Сначала при заданном q построим управление U qs ( t ) и траекторию X qs ( t ) . Затем укажем зависимость q ( s ) и тем самым получим формулы для задания минимизирующей последовательности { u s ( t ) , x s ( t ) }. Построение функций U qs ( t ) , X qs ( t ) производится с использованием рассмотренных в п. 2, 3 процедур. В узлах сетки (4.1) функция x_q ( t ) имеет разрывы по построению, причем на промежутках непрерывности функция посчитана при и = U E . Для аппроксимации кусочно-непрерывной траектории x_q ( t ) рассматривается в моменты t j ( j = 0, q ) предельная система (1.4) с краевыми условиями

x ( T i = 0) = x _Tj = ₀ = x q ( t j - 0) , x ( T f ) = x _T F = x q ( t j + 0) , (5.1) причем x_q ( 1 ₀ - 0) и x_q ( t_q + 0) означают x ₀ и x_q ( t_q ) .

Итак, в каждой точке разрыва функции x_q ( t ) рассматривается предельная система с условиями (5.1) и строится аппроксимация x ( t ) ее разрывной траектории x ( t ) в соответствии с описанными выше процедурами с той лишь разницей, что момент t _f заранее не известен (раньше мы задавали его равным 1) и граничные состояния не задаются (как в таблице 1), а определяются исходя из значений пределов слева и справа для x_q ( t ) в точках разрыва.

Пример 5. Используя полученные в примере 4 формулы для задания { x_q ( t ) }, построим аппроксимацию x s ( t ) для x_q ( t ) , указав зависимость q = q ( s ).

Для всех узлов t j по типу краевых условий имеем «особый» случай (п. 2.4). Управление U ²( t ) = 0 , т е [0, T F ] . Функция x^x ( t ) задается по формуле (2.3), где константа x¹ полагается произвольной - возьмем ее равной x q ( t j + 0) = x '( t j ) = - 1 , j = 0, q . По начальным данным x ¹⁴( T I ) = x q ’ ⁴( t j - 0) вычисляется число y_q ( t j ) , которое, вообще говоря, не равно значению y ( t j ) , где y ( t ) = - 2 1 . Поэтому в формуле (2.5) константа x ⁴ определяется исходя из орбиты Q ⁽ t j ., y_q ⁽ t j )) : х ⁴ = y q ⁽ t j ) ^{- (} x ¹⁾² = ^x T F .

y q ( j - ( T II )², T = 0,

, y_q ⁽ t j ) ^{- (} x ¹⁾²,    ^{T e (0,} r _F ],

Имеем: x^T ) = «

x ¹ = x 1 ( t> - 0), T = 0, ^T I     q j                  x\t ) = J

x1 = -1, те (0,Tf], x2, 3(т) = 0, те [0,Tf].

Для аппроксимации разрывной траектории x( T ) предельной системы в каждый момент t j рассматривается система вида (3.1).

Из условий x\ t ) = 1 L j + 1 1 , x '(0) = x q ( t j - 0) , x '( T F ) = x ¹ = x E ( t j + 0) = - 1 имеем при 1 ¹ =- 1 на [0, T _F ] решение x '( T ) = x q ( t j - 0) + ( 1/ L j - 1 ) t , т е [0, t _f ] , где T F определяется как момент достижения этой функцией заданного значения x T F = - 1 . Отсюда получаем T F = (( x q ( t j - 0) + 1) L j )[ ( L j - 1) . Решая задачу Коши t ( T ) = 1/ L j , t (0) = 0 и используя найденную формулу для T _F , находим формулу для длины X промежутков, на которых применяются большие по абсолютной величине управляющие воздействия:

t(TF ) =   =

Lj

( X q ( t j - 0) + 1) L j _ xq ( t j - 0) + 1

( L j - 1) L j

т At          At

Формула для L j : X := — ( r >  2 ), — = rr

L_j - 1 x q ( t j - 0) + 1

^ 0 при L j ^ ^ .

L_j - 1

О

_т , r ( x q ⁽ t j ^{- 0) +} 1 )

L = 1 +--------------, где r - j             At

доля длины шага A t = t_F/q , задающая длину X промежутков, на которых применяется (сравнительно) большое по абсолютной величине управление.

На первом отрезке [10,/,| точку, в которой происходит достижение функцией xqs (t) значения xE. =-1, будем обозначать 10s. Длина промежутка [10,10s ] равна X. Далее, на ин- тервале (10s, txs) функция xqs (t) находится интегрированием исходной системы с управлениями uE 2(t) = 0. На отрезке [t1 s, t1 ] функция xqs (t) вычисляется как решение начальной задачи для исходной системы с начальным условием x(t1 s) = xqs (t1 s), определяющим начальное состояние для предельной системы, рассматриваемой в момент t1 . Итак, в предельной системе краевые условия следующие: x(TI = 0) =xqs (t1 s )» x(TF ) = xq (t1 + 0).

На последующих частичных отрезках предельная система рассматривается только для правых концов t ₍ j _{+ 1) s} частичных отрезков. На промежутках [ t ₍ j _{+ 1) s} , t j _{+ 1}] интегрируется одна и та же система, но с разными начальными данными. По теореме о непрерывной зависимости решений от начальных данных заключаем, что значение x_qs ( t j _{+ 1}) не должно существенно отличаться от x_q ( t j _{+ 1} + 0) .

В момент 1 ₀ = 0 имеем y_q (0) = 0 . На отрезке [ 1 ₀, t 1 ] применяется управление:

^{-( 1} + r / ^A t ) ,

t е [0,10s ], uqs (t)=J UE (t) - 0,

- ( 1 + ( r ( x qs ( t 1 s ) + 1))/ a t )

t е ( t _{0 s} , t _{1 s} ),

1 - r ,     t e [ t , s , t , ],

(5.2)

где x qs ⁽ t 1 s ) = ^a t ^-

2A t

r

- 1 . Интегрируя систему при u ¹ = u qs ( t ) (рис. 6), находим

- rt / A t ,

t ^e [0, t о s ],

x qs_s ( t ) =^<

A t t ---1, r

t ^{e (} t 0 s , t 1 s ),

qs 0 s

A t + r

^^^^M

.

r

(2 - r ) t + r A t - 2 A t - 1,    t e [ t 1 _s , t 1 ],

Пусть, например, q = 5 , r = 4 . Тогда X = 0.05 ,

X is ( 1 0 s ) = - 1 ,

x 4 ( t о s ) =- 1.05,

x is ( t i s ) = - 0.9 , x is ( t i ) = - 1 (рис. 7).

На последующих частичных отрезках [ t j , t j _{+ 1}] ( j = 1, q - 1 ):

' u E ( t ) = 0,

t e ^[ t j , t ( j + 1) s ),

u is ⁽ t ) =^<

-

Г 1 + r ^{( xq} s ⁽ t ( j + 1) s ) ⁺ 1) 1

V

A t

- r ,

t ^{e [} t ( j + 1) s , t 1

(5.3)

где x \_s ⁽ t ( j + 1) s ) = ^A t

A t

^^^^M            ^^^^M

r

При r ^ ^ имеем x 1_qs ( t ( j + 1) s ) ^ x q ( t 1 ) = ^a t ^- 1 Пусть q ( s ) = s + 4 . Тогда

и

x qs ⁽ t ( j + 1) s ) ^ • x E ^—

- 1 при A t ^ 0 .

A t = -FL - , x 1 ( t J = -FL- 1 1 s + 4 s ¹ s     s + 4 V

^—     ^—

r

1 , x s ( t ( j + 1) s ) = st + 4 V ¹

^—     ^~

r

1 ,

tF

= A t

^{0 s} r    r ( s + 4) ,

.

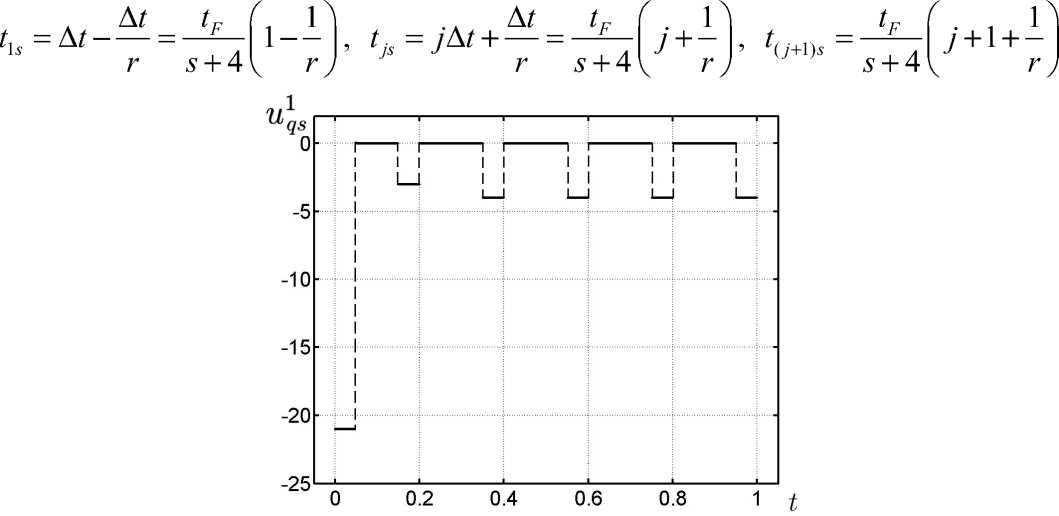
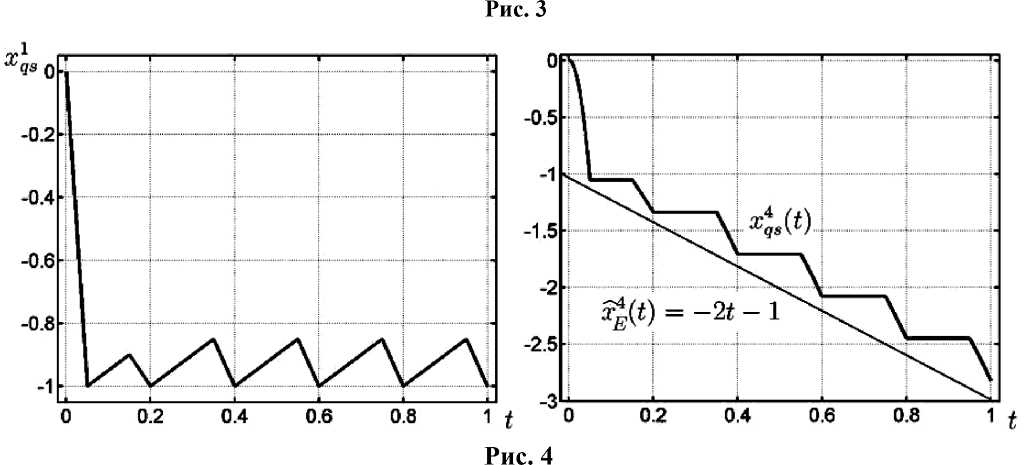
При фиксированном r (например, r = 4 ) и 5 ^ ^ имеем:

x ^{1 (} t ( j + 1) 5 ) ^ x E

¹ , t j + 1

A t    ~ tpj                 tp ( j + 1)

FF t (j+1) 5    r ^ 0, j ^ 5 + 4 tj , t (j+1) 5 ^ 5 + 4     tj+1 .

Используя формулы (5.2), (5.3), задающие явно управление u1qs(t) , построим численно аппроксимирующую траекторию xqs (t) и найдем соответствующее значение функционала I (uq-2("), xqJ4(')). Положим r = 4 и 5 = 1, тогда q(5) = 5, At = 0.2, X = 0.05 . В этом случае получаются функции uq5 (t) и xqJ4 (t), где q = q(5) = 5 , графики которых изображены на рис. 3, 4. Значение функционала I (uq- 2("), xqJ 4(")) = -1.81816 = inf I (u, x) = -2.

Таблица 2

s	q	I ( u 1 , x 1 )		s	q	I ( « 5 -!, x j-4 )
2	6	–1.8475		13	17	–1.9505
3	7	–1.8691		15	19	–1.9574
4	8	–1.8852		20	24	–1.9702
5	9	–1.8984		25	29	–1.9795
7	11	–1.9175		30	34	–1.9865
9	13	–1.9315		40	44	–1.9975
11	15	–1.9421

Считаем q = q ( 5 ) = 5 + 4 и r = 4. Проведем численные расчеты с использованием формул (5.2) и (5.3), увеличивая номер s . В таблице 2 представлены результаты вычислений.

Вычислительный эксперимент иллюстрирует, что I ( u 1 ^{- 2} ( - ), x 1 ^{- 4} ( - ) ) ^ inf I ( u , x ) = - 2 при 5 ^ ^ . □

Заключение

Основным результатом данной статьи является демонстрация возможности построения минимизирующих последовательностей и их специфики в системах, где условие Фробениуса не выполняется. Исследование основано на известном методе расширения исходной задачи до производной задачи [7], а также на предложенном в работах [11 – 13] подходе к построению допустимых в исходной системе траекторий предельной системы общего типа.

В статье рассмотрена ситуация, когда интеграл предельной системы выписывается в явном виде, что не всегда возможно. Перспективным является исследование ситуации с неявным описанием орбиты по аналогии с [7, 14]. В общем случае решение производной задачи будет находиться итерационно некоторым методом, работающим в невырожденных задачах. Поэтому в перспективе разработка итерационного метода улучшения управлений в терминах исходной задачи.